托管者有权重的动态门限多重密钥托管方案

李 林， 曹 瑀， 李志华*

(1.江南大学物联网工程学院，江苏无锡214122;2.大连理工大学软件学院，辽宁大连116024)

密钥托管技术主要解决安全密钥的分配与管理问题，它广泛运用于密钥保护与数据保密中，任何得到合法授权的密钥合成者可以从托管代理保存的密钥份额中恢复出安全密钥。

自Nechvatal提出门限密钥托管概念之后，国内外众多学者针对此进行了深入的研究与探讨。目前提出的大多数方案基于运算量与时间复杂度相对较高的RSA和ElGamal密码体制［1-2］;托管者权重单一且密钥份额只能使用一次［3］，而在实际运用中往往需要在一组托管代理组中共享托管多组密钥;需要维持安全的通信信道;存在逃避托管和无法验证子密钥的问题。

针对以上问题，文中在文献［2］的基础上，通过引入相对于RSA，ElGamal体制更具有优势的ECC密码体制和Shamir门限方案，利用ECC上的双线性对理论［4］及身份密码系统原理［5］，设计了门限值可变的动态多密钥托管方案。其中，每个托管代理具有不同的权重值，且其权重可以根据实际需要而变动［6-7］;同时，组合公钥(Combined Public Key，CPK)密码体制［8］的应用可以实现密钥份额与密钥托管代理的相互认证，解决了逃避托管与密钥份额篡改问题，且方案通信均在公共信道上进行，具有良好的应用前景。

1 方案初始化

设 Si={si1，si2，si3，…，sik}i∈［1，m］为方案中m组待托管密钥，p1，p2，…，pn为n个有权重的密钥托管代理，MD为多密钥分发者，DC为多密钥合成者。其中，MD和DC可以是密钥管理中心(Key Management Center，KMC)，也可以是某个安全的密钥托管代理。本方案需要一个公告牌，MD可以在公告牌上发布或者更新密钥参数信息，供托管方案中其他成员下载。

1.1 系统参数初始化

在多重密钥托管方案中，设E(Fq)为有限域上的一条安全的椭圆曲线［9］，G1和G2分别为两个q阶的加法群和乘法群，G为G1的生成元，且它们之间存在双线性映射e:G1×G1→G2;h:{0，1}*→G1和h1:{0，1}*→为两个单向hash函数;hk(·)为带密钥的钥控单向hash函数;(Ek，Dk)为某对称算法的加解密算法，E2是椭圆曲线公开密钥加密算法。然 后 在 公 告 牌 上 公 布 {E(Fq)，e，G，q，h0，h1，hk(·)}。

1.2 托管代理初始化

密钥托管代理的公私钥对由基于ECC的CPK算法初始化生成，KMC随机选取r∈［1，q-1］，其椭圆曲线E(Fq)上一点Pk=rG=(Xr，Yr);利用整数矢量kij秘密构造私钥种子矩阵SSK，则对应的公钥种子矩阵PSK由点矢量kijG=(xij，yij)构成，公开{Ii，PSK};KMC对每个托管代理身份It(设序列位数为h)利用hash函数h1作行映射后，私钥为

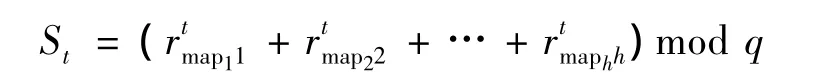
其中，rmapkh为SSK中的第k列中的第mapk个值。任何托管代理均可利用公开的{It，PSK}计算出公钥:

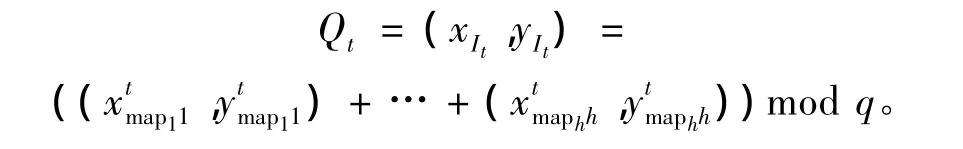
2 动态多重密钥共享协议

文中基于椭圆曲线密码体制提出了动态的多密钥共享(ECC-based dynamic multi-key sharing protocol，EDMSP)协议，包括多密钥分发、子密钥份额验证、多密钥重构等部分。

2.1 多密钥的分发

多密钥分发者MD利用下面的算法将m组密钥Si={si1，si2，si3，…，sik}分发给密钥托管组P={p1，p2，…，pn}，其权重为 W={w1，w2，…，wn}。对于每组密钥而言，该协议可以认作为一个(ti，n)门限密钥共享方案，密钥分发过程如下:

1)MD从［1，q-1］中随机选取整数 ri0∈［1，q-1］，计算 Ri0=rioG。

2)MD随机构造m个ti-1次多项式:

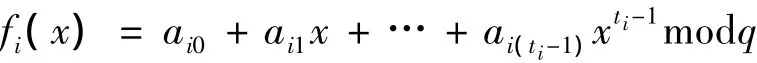
其中，ai0=SMD;aiti-1≠0，且ai1，…，aiti-1∈GF(Q)。

3)MD 计算 Aij=aijG(j=0，2，…，ti-1)，

其中，8表示按位异或运算。销毁aij并公布s'il。

4)MD随机选取 α∈ GF(p)，计算 Dit=fi(It)Ri0(t=1，2，…，n)以及 git=h(Dit·+ri0Qt)，lit=f(It)-h(Dit·+ α·giti)，将{It，Wt，Dit}传递给密钥托管者It，并公布有序数组{α，lit，It，Wt}。

5)MD随机选取bi0∈，计算

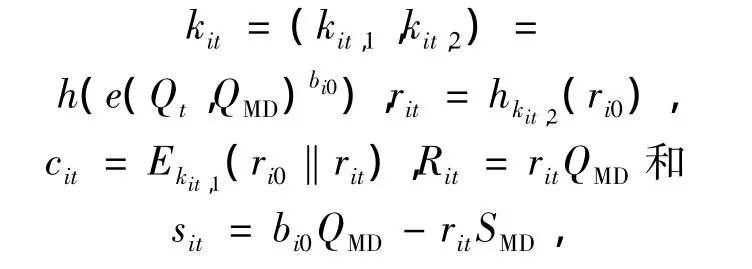
并将(cit，sit，Rit)传递给密钥托管组 P，ri0销毁。

2.2 子密钥份额验证

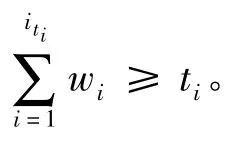
1)pi获取(cit，sit，Rit)后，计算

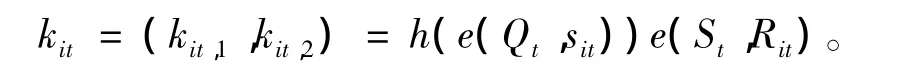
2)pi利用得到的 kit解密 Dkit，1(cit)，并验证等式rit=hkit，2(ri0)是否成立。若成立，则临时密钥传递成功;否则，向MD传递错误信息，并停止通信。

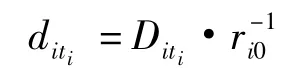
2.3 多密钥重构

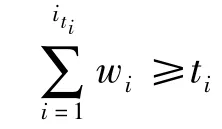
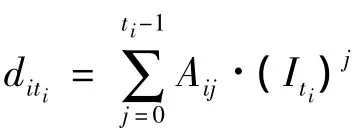
2)DC将计算得到的ti个数值对(Iti，fi(Iti))利用拉格朗日多项式插值重构［11］，具体如下:

3)DC计算Aij=aijG，并与公告牌上的{Aij}比较，验证恢复出来的常数项的正确性。若正确，则计算sil=s'il8ai08…8aij，从而得到共享的秘密组Si={si1，si2，si3，…，sik}。

3 基于动态多重密钥共享协议的密钥托管方案

在密钥托管方案中，{KMC}负责颁发证书，监听服务器{W}，经必要授权可以与密钥托管组P，{KMC}、密钥合成者DC等执行相应的协议监听用户通信。

基于动态多密钥共享协议的多密钥托管方案(EDMSP-based key escrow scheme，EKES)描述如下。

3.1 证书颁发

在EDMSP协议中子密钥验证阶段，当密钥托管子集pi中的每个成员验证通过收到的托管密钥份额后，计算签名 ssti= sigIt(h(MD，giti，ziti=h(diti+ri0·Sti·G)·Gmodp))，并将(MD，giti，ziti，ssti)传递给KMC。

密钥管理中心接收到密钥托管子集pi的(MD，giti，ziti，ssti)后，验证 ziti=gitiGmodp 和签名是否成立。若成立，则可以确认签名ssti有效，并计算签名sK=sigKMC(h(MD，G，p，QMD))，并为 MD 颁发证书 C(MD)=(MD，p，G，QMD，sK)，认定组密钥 Si托管成功。

3.2 通信协议的设计

当用户B获取到证书C(MD)时，秘密选取Ktmp，l∈，(其中Ktmp作为临时会话密钥加密消息)，并向 MD 发送{Ek(M，Ktmp)，LEAF}。

其中:

S(H(M，T))为B用椭圆曲线私钥对H(M，T)的签名［12］。

MD收到{Ek(M，Ktmp)，LEAF}后计算 Ktmp=v-SMD·u，利用Ktmp计算明文M=D(C，Ktmp)，求取H(M，T)。若H(M，T)满足签名方案，MD可以确认收到的M是有效，开始通信并传递组密钥。

3.3 监听协议的设计

监听服务器接收到合法的监听授权时，利用监听协议对监听对象的通信内容进行有效监听。

1)监听服务器{W}首先将授权证书和监听到的LEAF分别出示给任意合格托管组Pi中的每一个托管代理Iti，托管代理验证证书的有效性与时效性后计算:

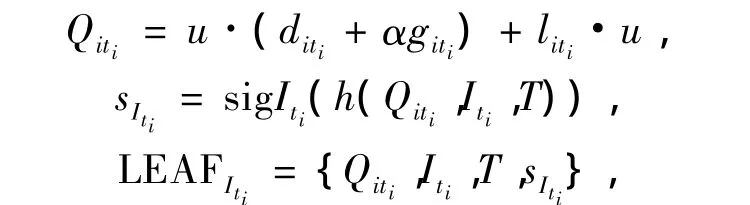
并将LEAFIti回传给监听服务器。

2)监听服务器接收到LEAFIti后，验证时效性及h(Qiti，Iti，T)是否满足签名方案。若满足，则监听服务器认为托管代理诚实出示了Qij，并计算:

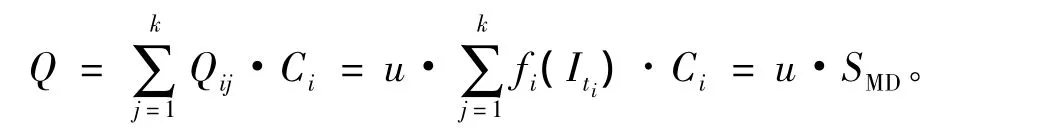
由Ktmp=v-lQMD恢复出Ktmp，再由Ktmp解密出通信明文M=D(C，Ktmp)，最后验证H(M，T)是否满足签名。若满足，则监听服务器实现用户B的通信监听。

4 方案分析和证明

4.1 正确性分析

定理1 方案具有身份认证功能。在子密钥份额验证阶段，由双线性变换性质［13］可知，只有对应身份的托管代理才可以进行解签密，有 e(Qt，sit)e(St，Rit)=e(Qt，QMD)bi0恒成立。

证

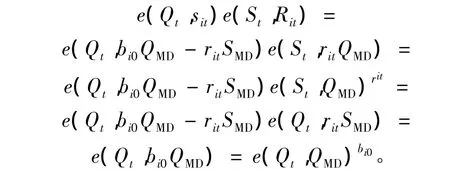
证毕。

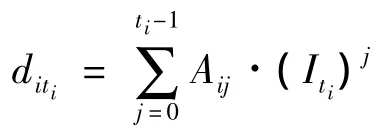
证

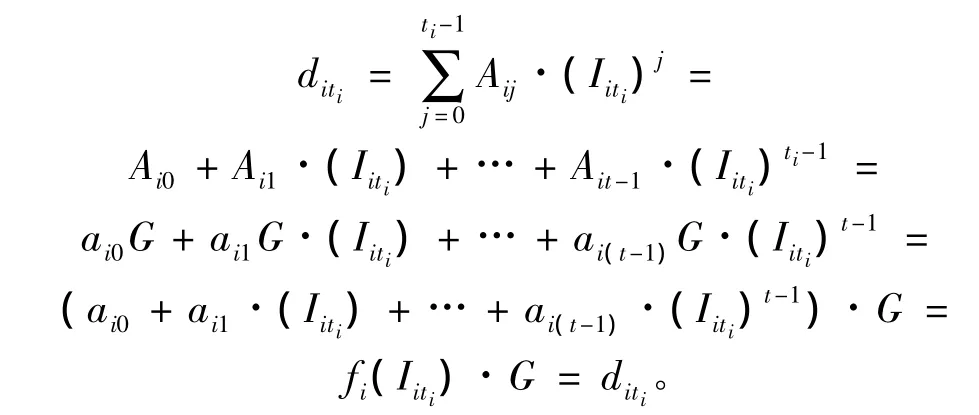
证毕。

定理3 EDMSP协议具备前向安全性，即在多密钥分发阶段，即使多密钥分发者私钥泄露也不会影响之前所共享的核心参数ri0的安全性。

证当多密钥分发者的私钥SMD泄露时，攻击者想要利用Rit=ritQMD计算得到rit面临着破解椭圆曲线离散对数难题(Elliptic Curve Discrete Logarithm Problem，ECDLP)。在多项式时间内，计算上是不可行的。同理，攻击者也无法计算出参数bi0。因此，攻击者无法计算出 kit=(kit，1，kit，2)。在分发者私钥泄漏的情况下，无法解密得到核心参数ri0，因此无法进行后续攻击行为。由此证明了协议具有前向安全性。

4.2 安全性分析

文中提出的多密钥托管方案的安全性基于ECC密码体制、Shamir门限方案以及单向hash函数的安全性，分析如下:

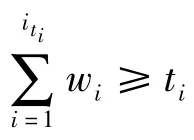
2)在密钥分发阶段，由于传递的是影子份额［15］，方案中密钥托管代理和恶意的攻击者无法从公开的参数获取任何关于aij以及fi(It)的私密信息。攻击者想要破解这些信息意味着要破解椭圆曲线上的离散对数难题，在计算上是不可行的。因此，可以防范外部攻击者对合法托管代理的攻击。

3)在密钥重构阶段，由定理2可知，只有正确的密钥托管者提供的正确份额才能参与组密钥的重构，有效防止了托管代理对DC的欺诈，即实现了密钥份额的验证。

4)方案中KMC验证了托管代理密钥份额的有效性和真实性后为MD生成证书，有效地避免了分发者逃避托管。在监听阶段，监听服务器收到托管代理的LEAFIti后，验证其是否来源于诚实的托管代理，再计算Q与当次的会话密钥Ktmp，而不是用户的任何私钥信息，且每次通信用户B都会随机选取l。因此，避免了“一次监听，永久监听”的问题。

4.3 性能分析

从以下几方面分析文中方案的性能:

1)对于时间复杂度。由安全性证明可知，该方案不需要维持安全信道，降低了方案的实现代价。在密钥分发阶段，由于椭圆曲线倍点运算的时间复杂度为o(n2)远小于模幂运算与大数运算，且密钥长度较短，因此该方案的时间复杂度低于其他方案。

2)对于动态性。当托管代理组P新增代理In+1时，首先计算出公私钥对{SIn+1，QIn+1}，然后计算Di(n+1)=fi(In+1)Ri0，并将{In+1，Di(n+1)，Wn+1}传递给密钥托管代理。若方案中某个密钥托管代理It不可信或密钥份额泄漏时，只需回收该用户身份It与托管份额，重新选择一个多项式即可。

3)对于安全性基础。椭圆曲线密码体制的安全强度以及椭圆曲线离散对数问题的难解性都远大于传统的离散对数系统以及大数分解问题，且采用椭圆曲线上的双线性对理论，可以使方案以较短的密钥长度得到相对于其他密码系统同等的安全强度，取消了方案中临时密钥传递过程中多余的交互过程，从而降低了通信复杂度，更加符合实际的应用需求。

4)对于前向安全性。当多密钥分发者的私钥SMD泄露时，由定理3与安全性分析可知，MD传递的临时会话私钥ri0是不会被任何攻击者获取，所以攻击者无法计算出传递给托管代理的密钥份额diti。因此，MD的私钥泄露不会对前面传递的密钥份额造成安全威胁，即方案具备前向安全性。

5)由于在密钥分发阶段，不同的密钥组构造的曲线fi(x)以及选取的随机整数ri0不同，由安全性证明可知，一组密钥的重构不会影响其他托管组密钥的安全性与重构。同时方案中托管代理的密钥由用户身份计算产生，因此在多组密钥共享托管时，实现了托管密钥与代理身份的对应认证，且各托管代理的密钥以及影子份额可以重复利用。

表1列出了文中方案与其他方案的对比结果。

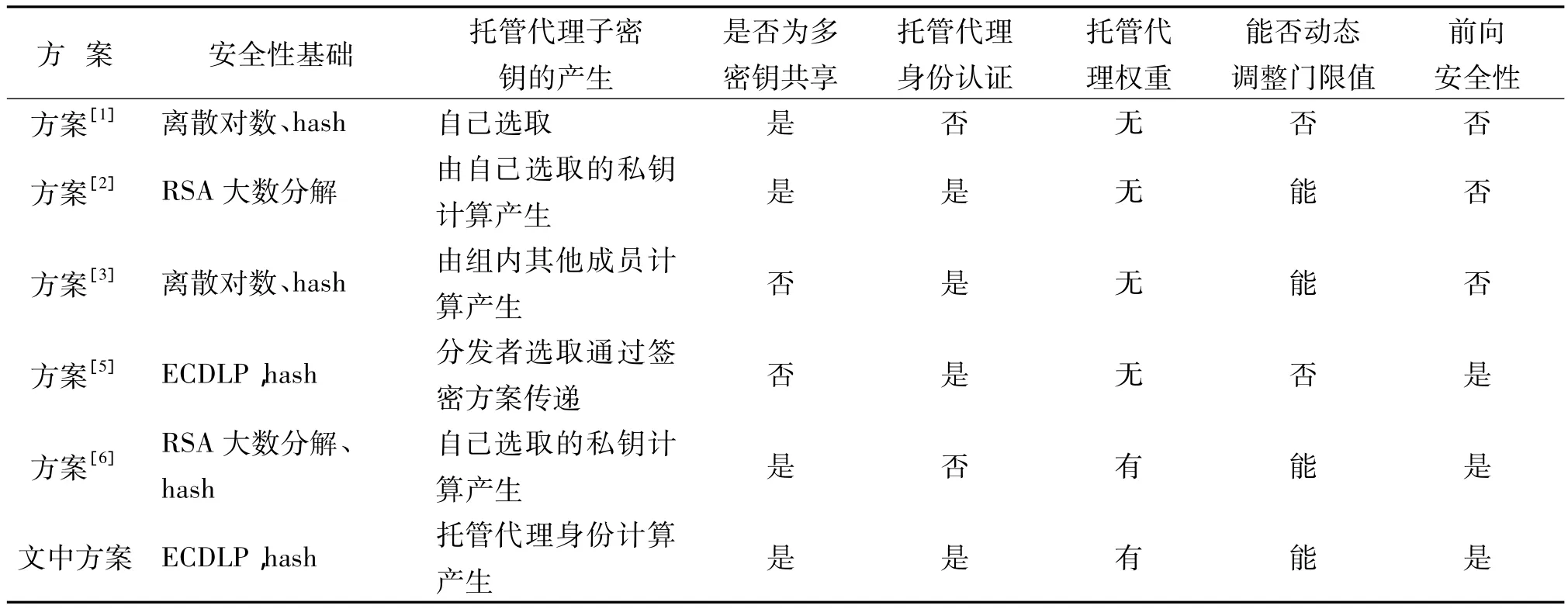
表1 文中方案与现有方案的性能比较Tab.1 Performance comparisons of the scheme with existing schemes

5结语

文中基于动态多密钥共享协议提出了参与者有权重的门限多密钥托管方案。方案中密钥分发者可以根据密钥的重要性动态调整门限值，而且可以根据密钥托管者的等级调整权重值，当权限值相同时，方案可退化为普通的门限托管方案。该方案还可以防止密钥分发者与托管代理的欺诈，特别是双线性对的运用，方案可以在不增加信息交互的情况下传递参数，降低了通信开销，具有良好的前向保密性。因此，文中提出的密钥托管方案具有良好的应用前景。

［1］杨捷，李继国.基于密钥协商的门限多秘密共享方案［J］.计算机工程，2010，36(20):153-154.

YANG Jie，LI Jiguo.Threshold multi-secret sharing scheme based on key agreement［J］.Computer Engineering，2010，36(20):153-154.(in Chinese)

［2］乔晓林，张建中.一种动态门限多组秘密共享方案［J］.计算机工程，2010，36(22):143-146.

QIAO Xiaolin，ZHANG Jianzhong.Dynamic threshold multi-group-secret sharing scheme［J］.Computer Engineering，2010，36(22):143-146.(in Chinese)

［3］周孟创，余昭平.一个无可信中心的动态(t，n)门限密钥共享方案［J］.计算机应用研究，2011，28(8):3061-3063.

ZHOU Mengchuang，YU Zhaoping.Dynamic(t，n)threshold key sharing scheme without trusted party［J］.Application Research of Computers，2011，28(8):3061-3063.(in Chinese)

［4］黄伟达，姚国祥，沈瑞雪.基于双线性对的动态门限多秘密共享方案［J］.计算机工程与设计，2012，33(3):901-905.

HUANG Weida，YAO Guoxiang，SHEN Ruixue.Dynamic threshold multi-secret sharing scheme based on bilinear pairing［J］.Computer Engineering and Design，2012，33(3):901-905.(in Chinese)

［5］庞辽军，裴庆祺，王育民，等.基于ID的门限多重秘密共享方案［J］.软件学报，2008，19(10):2739-2745.

PANG Liaojun，PEI Qingqi，WANG Yumin，et al.An identity(ID)-based threshold multi-secret sharing scheme［J］.Journal of Software，2008，19(10):2739-2745.(in Chinese)

［6］王伟，周顺先.参与者有权重的多重秘密共享方案［J］.计算机应用，2010，30(12):3334-3336.

WANG Wei，ZHOU Shunxian.Multi-secret sharing scheme among weighted participants［J］.Journal of Computer Applications，2010，30(12):3334-3336.(in Chinese)

［7］Yoo Seongmin，Park Pyungkoo，Ryou Jaecheol，et al.Key sharing scheme based on one weighted threshold secret sharing［C］//Advanced Communication Technology(ICACT).Pyeongchang:IEEE，2013.

［8］邵春雨，苏锦海.基于组合公钥的用户公钥认证算法［J］.计算机工程，2011，37(4):145-146.

SHAO Chunyu，SU Jinhai.User public key authentication algorithm based on combined public key［J］.Computer Engineering，2011，37(4):145-146.(in Chinese)

［9］国家密码管理局.GM/T 0003.1—2012.SM2椭圆曲线公钥密码算法［S］.北京:国家标准出版社，2012.

［10］乔晓林，张建中.基于ECC的多组织间的多级秘密共享方案［J］.计算机工程与应用，2011，47(20):56-57.

QIAO Xiaolin，ZHANG Jianzhong.Multi-stage secret sharing scheme among multiple organizations based in ECC［J］.Computer Engineering and Applications，2011，47(20):56-57.(in Chinese)

［11］luksan L，Matonoha C，Vlcek J.On lagrange multipliers of trust region subproblems［J］.Bit Numerical Mathematics，2008，48(4):763-768.

［12］孙荣燕，蔡昌曙，周洲，等.国密SM2数字签名算法与ECDSA算法对比分析研究［J］.网络安全技术与应用，2013(2):60-62.

SUN Rongyan，CAI Changshu，ZHOU Zhou，et al.The comparision between digital signature based on SM2 and ECDSA［J］.Network Security Technology and Application，2013(2):60-62.(in Chinese)

［13］张建中，张艳丽.一个双线性对上公开可验证多秘密共享方案［J］.计算机工程与应用，2011，47(25):82-84.

ZHANG Jianzhong，ZHANG Yanli.Public verifiable multi-secret sharing scheme on bilinear pairing［J］.Computer Engineering and Applications，2011，47(25):82-84.(in Chinese)

［14］张永，张欢.基于椭圆曲线的密钥共享方案［J］.计算机工程与应用，2014，50(8):90-92.

ZHANG Yong，ZHANG Huan.Secret sharing scheme based on elliptic curve［J］.Computer Engineering and Applications，2014，50(8):90-92.(in Chinese)

［15］Manik Lal Das.A key escrow-free identity-based signature scheme without using secure channel［J］.Cryptologia，2010，35(1):58-72.