基于蜂群优化或分解的二维Arimoto灰度熵阈值分割
吴一全,殷 骏,朱 丽,袁永明
(1.南京航空航天大学电子信息工程学院,江苏南京210016;2.农业部淡水渔业和种质资源利用重点实验室中国水产科学研究院淡水渔业研究中心,江苏无锡214081;3.农业部渔业装备与工程技术重点实验室,上海200092;4.江苏省制浆造纸科学与技术重点实验室,江苏南京210037)
基于蜂群优化或分解的二维Arimoto灰度熵阈值分割
吴一全1,2,3,4,殷 骏1,朱 丽1,袁永明2
(1.南京航空航天大学电子信息工程学院,江苏南京210016;2.农业部淡水渔业和种质资源利用重点实验室中国水产科学研究院淡水渔业研究中心,江苏无锡214081;3.农业部渔业装备与工程技术重点实验室,上海200092;4.江苏省制浆造纸科学与技术重点实验室,江苏南京210037)
现有的Arimoto熵阈值法未考虑图像目标和背景的类内灰度均匀性,为此提出基于蜂群优化和基于分解的二维Arimoto灰度熵阈值分割方法.定义Arimoto灰度熵,导出二维Arimoto灰度熵阈值法,分别利用基于蜂群优化和基于分解的方法求解最佳阈值.基于蜂群优化方法给出中间变量的快速递推公式,利用改进的人工蜂群(MABC)优化算法搜索最佳阈值,减少迭代时适应度函数中的冗余运算.基于分解方法将求解二维Arimoto灰度熵阈值法的运算转化到2个一维空间,进一步降低计算复杂度.实验结果表明:与近年来提出的3种同类方法相比,所提出方法的分割性能更优,分割后图像中目标完整、边缘纹理清晰,具有良好的抗噪性.同时,所提出的方法运行速度快,有望满足实际系统对分割的实时处理要求.
图像处理;阈值分割;二维Arimoto灰度熵;改进人工蜂群优化算法;分解;快速递推算法
图像分割是图像处理与分析中的关键步骤,目的是提取图像中感兴趣的区域,便于后续的图像特征提取与识别.阈值分割是一种简单、快速、有效的图像分割方法,根据目标和背景区域中灰度分布的差异性,选取一定的灰度阈值,以分离背景区域与感兴趣的目标区域.目前已存在大量的阈值分割方法[1-3].其中,基于熵准则的阈值分割方法因其性能稳定且实现简单而得到广泛应用.Kapur等[4]最先将信息熵的概念引入阈值分割,提出了一维最大Shannon熵阈值法.然而,一维直方图没有考虑图像像素的空间信息,当图像受到噪声干扰时,一维阈值法的分割效果不够理想.因此,Brink[5]进一步利用灰度-邻域平均灰度二维直方图,提出了二维最大Shannon熵阈值法.由于Shannon熵具有可加性,Shannon熵阈值法会忽略目标与背景灰度分布间的相关性.为此,龚劬等[6-7]提出了基于Renyi熵、Tsallis熵的二维阈值分割方法,而当参数相同时,2种方法得到的阈值相同[8].近年来,Arimoto熵被引入阈值分割.Arimoto熵是一种适用于处理决策误差的广义熵,且能得到误差概率的上界.卓问等[9-10]提出了二维Arimoto熵阈值法,性能优于二维Renyi熵阈值法.然而二维Arimoto熵仅依赖于二维灰度直方图的概率信息,并没有直接反映图像类内的灰度均匀性,这使得二维Arimoto熵阈值法对某些图像的分割效果不佳.与一维阈值法相比,二维阈值法的分割精度更高,然而其运行速度却大大降低.人们常采用快速递推公式,将二维阈值法的计算复杂度从O(L4)减少为O(L2)(L为图像的灰度级数目).此外,遗传算法、粒子群算法[11-12]、人工蜂群(artificial bee colony,ABC)算法[13]等一系列群体智能优化算法也相继被引入到二维阈值分割中,进一步缩短了运行时间.其中,ABC算法是较好的智能优化算法,具有计算简单、需要调整的参数少等优点,然而ABC优化算法存在收敛速度慢、易陷入局部极值的问题[14].同时,基于群体智能优化算法的阈值分割法在每次迭代计算适应度函数的过程中,存在大量冗余运算.
鉴于上述问题,本文首先定义Arimoto灰度熵,在Arimoto熵的基础上,进一步考虑了图像目标和背景类内的灰度均匀性.然后结合灰度-平均灰度直方图,给出二维Arimoto灰度熵的阈值选取公式.为了减少运算量,提出基于蜂群优化和基于分解的二维Arimoto灰度熵阈值分割方法.基于蜂群优化的二维Arimoto灰度熵阈值分割方法利用一种改进的人工蜂群(modified artificial bee colony,MABC)优化算法[15]搜索阈值,同时利用快速递推公式消除适应度函数中的冗余计算,MABC优化算法在ABC优化算法的基础上引入了混沌算子、相对基于学习策略及差分进化算法,可同时加强蜂群的全局和局部搜索能力,从而提高蜂群算法的收敛速度和寻优精度.基于分解的二维Arimoto灰度熵阈值分割方法将二维Arimoto灰度熵阈值选取转化到2个一维空间上,将计算复杂度进一步减少为O(L).利用本文提出的2种方法对大量灰度图像进行了阈值分割实验,并与二维Tsallis熵阈值法[7]、二维Tsallis交叉熵阈值法[11]、二维Arimoto熵阈值法[10]的分割结果及算法运行时间进行比较.
1 基于改进蜂群优化的二维Arimoto灰度熵阈值分割方法
1.1 Shannon熵的定义
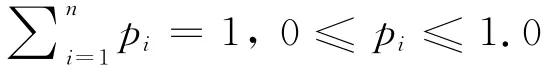
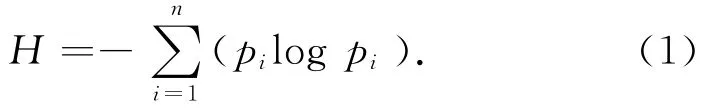
若存在相互独立的随机变量X和Y,则Shannon熵满足如下条件:
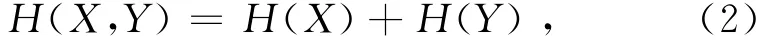
即Shannon熵是可加性熵,而图像信息量的特点是不可加性,因此,传统基于Shannon熵的阈值分割方法效果不佳.
1.2 一维Arimoto灰度熵阈值法
Arimoto熵的形式类似于向量的R-范数,定义如下[16]:
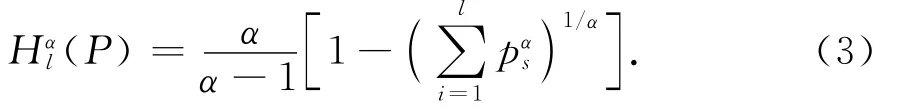
式中:α>0,α≠1为常数;
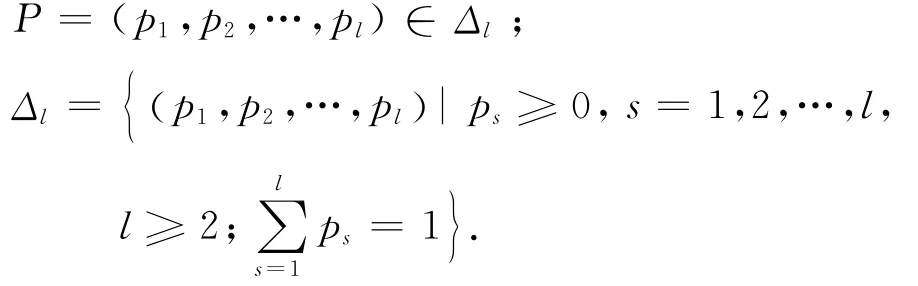
当α→1时,Arimoto熵等同于Shannon熵.
Arimoto熵具有伪可加性.若X和Y是相互独立的随机变量,那么
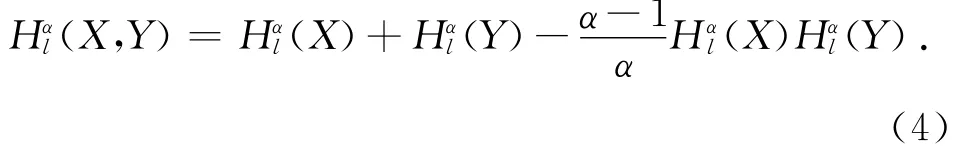
由于Arimoto熵无法直接反映图像目标和背景类内灰度的均匀性,对于含丰富纹理的图像分割效果不佳[17].根据文献[17]定义的Shannon灰度熵,导出Arimoto灰度熵,并给出其一维阈值选取公式.设给定一幅灰度级数目为L的图像,像素(m,n)的灰度级为f(m,n),h(i)表示灰度级为i的像素出现的频数.用阈值t将图像划分为目标类Co和背景类Cb,其中Co的像素灰度级位于[0,t],Cb的像素灰度级位于[t+1,L-1].令
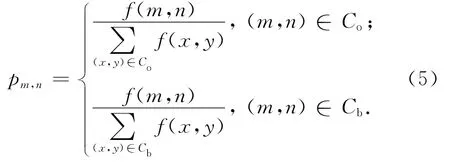
目标类的Arimoto灰度熵可表示为
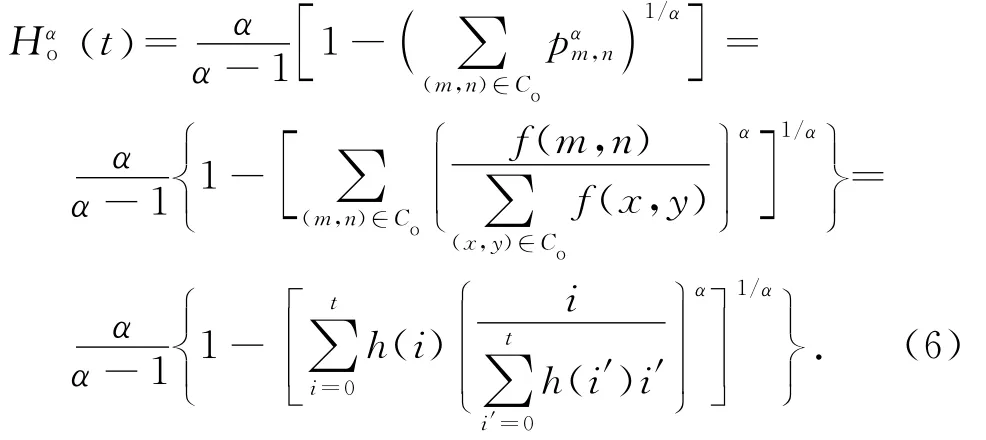
背景类的Arimoto灰度熵可表示为
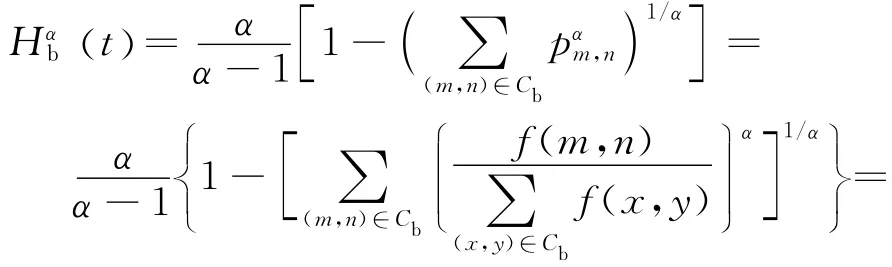
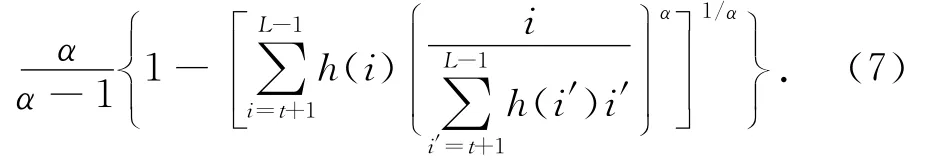
那么,图像的总Arimoto灰度熵为
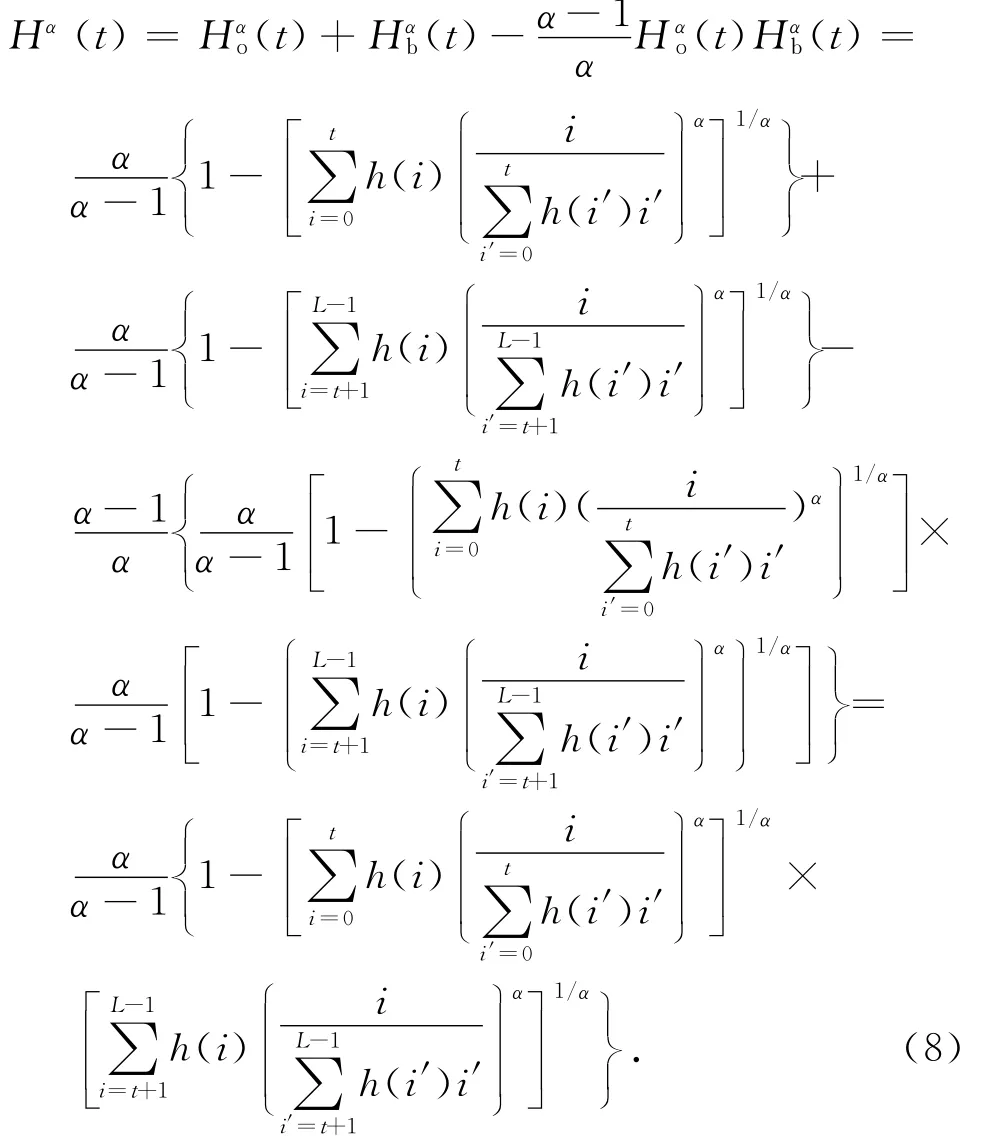
总Arimoto灰度熵越大,图像目标类内灰度差异与背景类内灰度差异的和越小,图像类内灰度级越趋于均匀.当总Arimoto灰度熵Hα(t)达到最大值时,得到一维Arimoto灰度熵方法的最佳阈值T*:
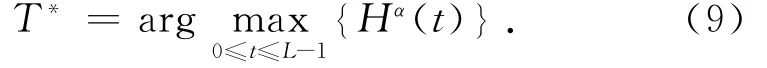
1.3 二维Arimoto灰度熵阈值法及其快速递推公式
设给定一幅大小M×N的图像,像素为(m,n),灰度级为f(m,n),其邻域平均灰度级为g(m,n),二元组(i,j)(i为灰度级,j为邻域灰度级)出现的频数为h(i,j),则二维灰度-平均灰度直方图的值
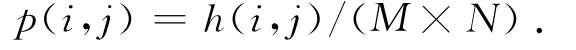

图1 二维直方图的区域划分Fig.1 Region division in 2D histogram
假设图像由暗目标、亮背景构成,那么区域0代表目标区域C′o,区域1代表背景区域C′b,区域2和区域3代表噪声和边缘.噪声与边缘的像素数目在整幅图像中所占比重很小,因此,其出现的概率可假设为0.
定义目标区域C′o的二维Arimoto灰度熵向量为
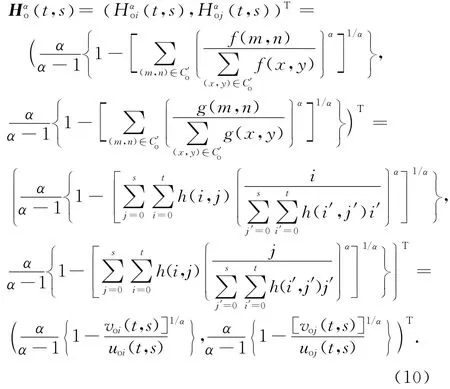
式中:
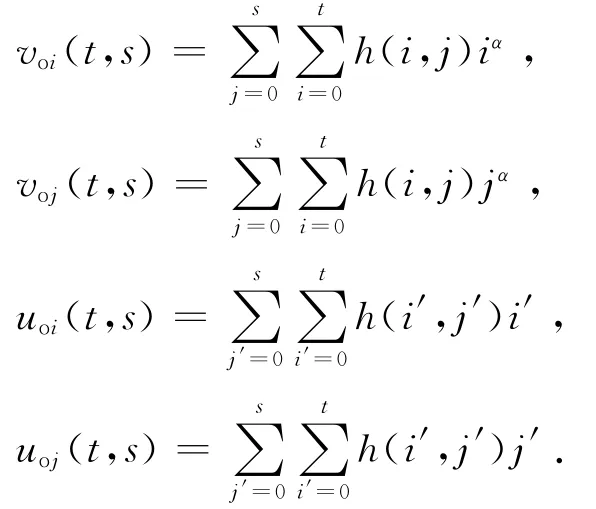
背景区域C′b的二维Arimoto灰度熵向量为
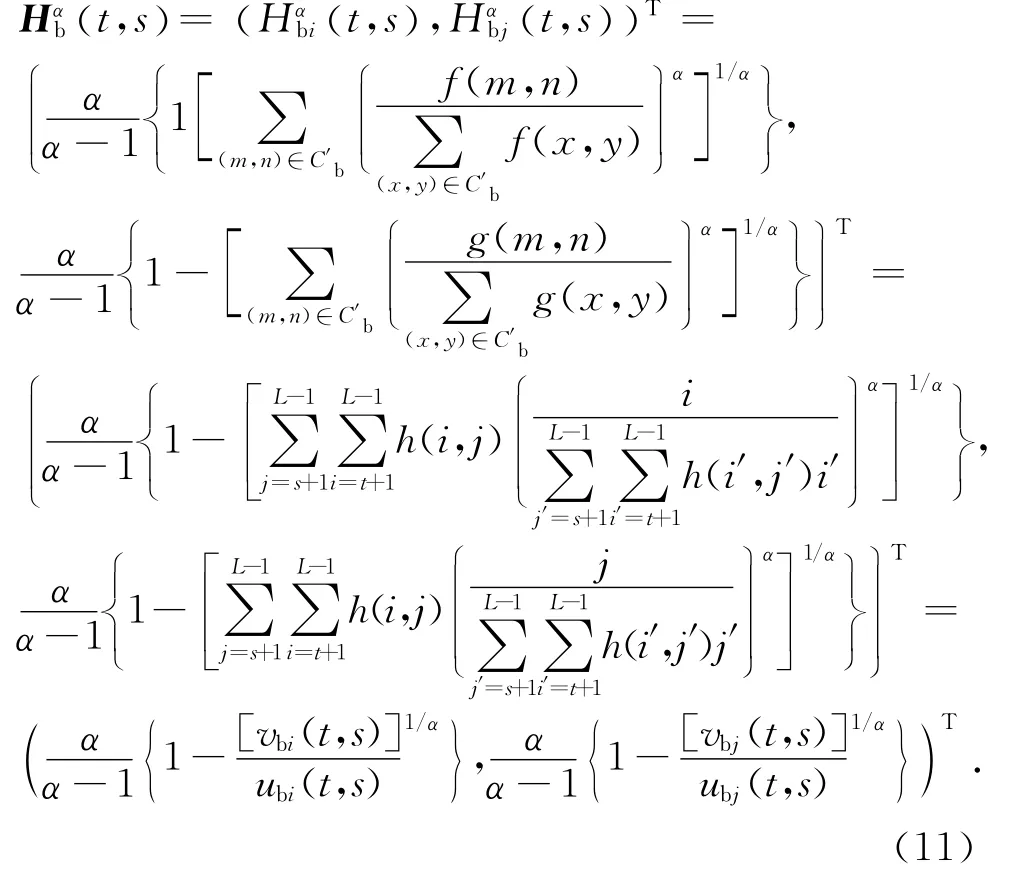
式中:
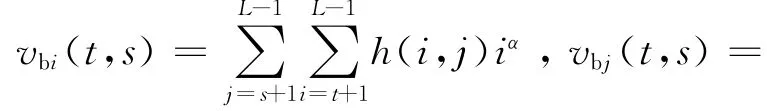

图像的总二维Arimoto灰度熵向量为
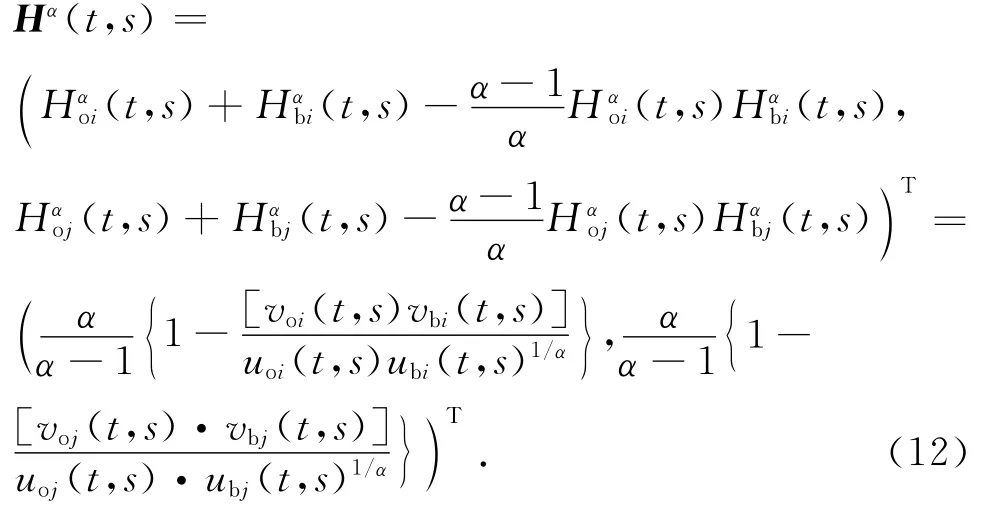
二维Arimoto灰度熵阈值法的准则函数为
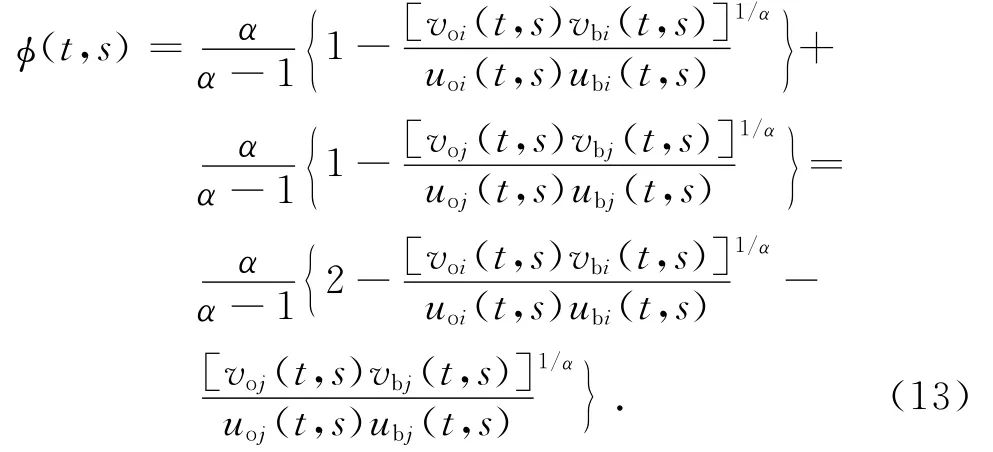
那么,当φ(t,s)达到最大值时,得到二维Arimoto灰度熵方法的最佳阈值:
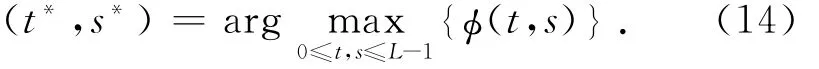
为了降低上述二维Arimoto灰度熵方法的运算量,可借助快速递推公式计算中间变量,使复杂度从O(L4)降低为O(L2).以voi( t,s) 为例,其递推公式如下:
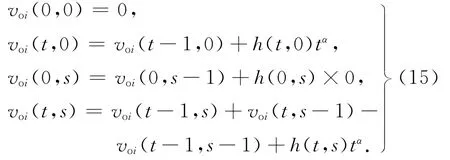
按照上述类似的方式,可以写出其他7个中间变量voj(t,s)、uoi(t,s)、uoj(t,s)、vbi(t,s)、vbj(t,s)、ubi(t,s)、ubj(t,s)的递推公式.
1.4 二维Arimoto灰度熵阈值选取的蜂群优化算法步骤
ABC优化算法是模拟蜂群觅食行为的群体智能优化算法,通过雇佣蜂、观察蜂、侦察蜂的协同搜索,寻找最佳蜜源以及问题的最优解.ABC优化算法的基本思路是利用雇佣蜂寻找多个食物源,并在其周围搜索最优解,利用观察蜂在雇佣蜂搜索到的较好食物源周围搜索.当数次迭代后,雇佣蜂仍停滞在某个食物源,则雇佣蜂变为侦察蜂,随机寻找新的食物源.
设在n*维解空间,初始化S只雇佣蜂,第a只雇佣蜂的食物源位置向量Zi=(za,1,za,2,…,za,n*),各食物源位置由下式随机产生:
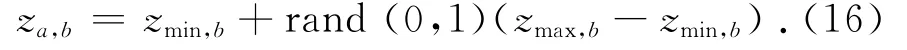
式中:a=1,2,…,S,b=1,2,…,n,zmin,b和zmax,b分别为第b维食物源位置的下限和上限.
然后,雇佣蜂在当前食物源周围搜索,寻找适应度值更优的新食物源,位置更新公式如下:
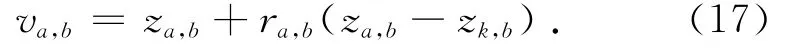
式中:a≠k,ra,b是均匀分布在[-1,1]的随机数.
根据雇佣蜂搜索到食物源的适应度值选择观察蜂继续在该食物源附近搜索,适应度值越大,选择的概率越高.当食物源位置连续M0次未变化时,该处的雇佣蜂变成侦查蜂,依据式(14)重新随机初始化自身的位置.
上述基本ABC优化算法存在收敛速度慢、易陷入局部极值的缺点,下文利用MABC优化算法搜索最佳阈值.MABC优化算法在ABC优化算法基础上进一步引入混沌算子、相对基学习策略以及差分进化算法,可提高收敛速度及搜索精度.
首先利用混沌算子和相对基学习方法初始化位置向量,混沌迭代公式如下:

式中:ck∈(0,1),k=1,2,…,K,K为最大迭代次数.式中的映射变量具有遍历性、随机性及不规则性.根据该变量初始化S个食物源:
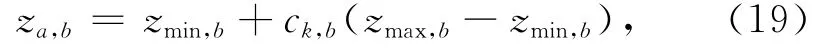
并根据相对基学习方法初始化另一组食物源:
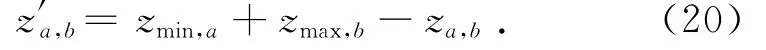
然后选择较好的食物源进行搜索,并采用差分进化法在当前最优食物源zbest,b附近进行搜索:
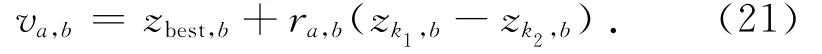
式中:a、k1、k2互不相同.该位置进化公式可加快收敛速度,提高局部搜索能力.为了避免在局部极值处收敛,当位置未更新时,采用式(17)进行全局搜索.
基于MABC优化算法的二维Arimoto灰度熵阈值分割方法的具体步骤如下.
1)初始化蜂群.最大迭代次数M1=50,食物源位置连续不变上限次数M2=20,维数取2,即对二维阈值(t,s)进行搜索.依据式(18)~(20),产生2S个食物源,依据式(13)计算食物源的适应度函数值,适应度值越大,食物源越优,选择较优的S个食物源.
2)依据式(21)更新食物源位置,若新食物源适应度函数值较高,则代替原食物源,并转步骤4);否则转步骤3).
3)若rand(0,1)<β(β为平衡全局搜索和局部搜索能力的算子,本文取0.7),则依据式(17)更新食物源位置,选择较优的食物源,否则直接转步骤4).
4)若迭代次数达到M1或食物源位置连续不变次数达到M2,输出此时搜索到的食物源位置,即最佳二维阈值(t*,s*),并对图像进行分割,否则转至2).
2 基于分解的二维Arimoto灰度熵阈值分割方法
在区域2和区域3中的像素出现概率为0这一假设下,可将求解二维Arimoto灰度熵方法的二维最佳阈值转化为计算2个一维最佳阈值,即对原始灰度图像和邻域平均灰度图像分别采用一维Arimoto灰度熵方法求解2个一维阈值,再组合成二维最佳阈值.
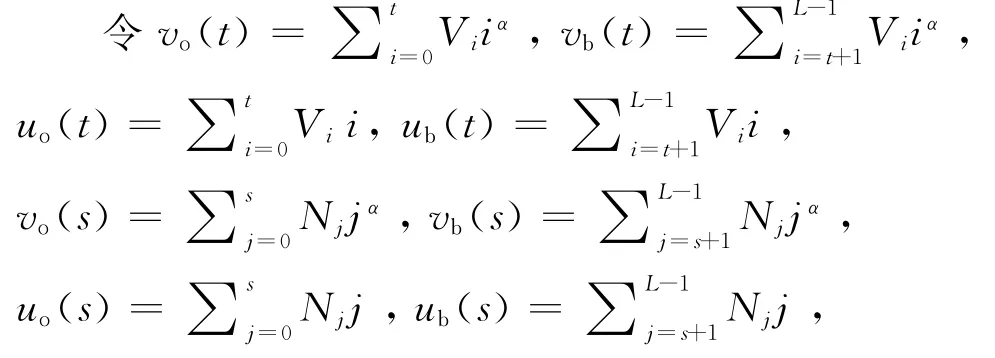
那么,原始灰度图像和邻域平均灰度图像的一维Arimoto灰度熵阈值分割的准则函数分别为
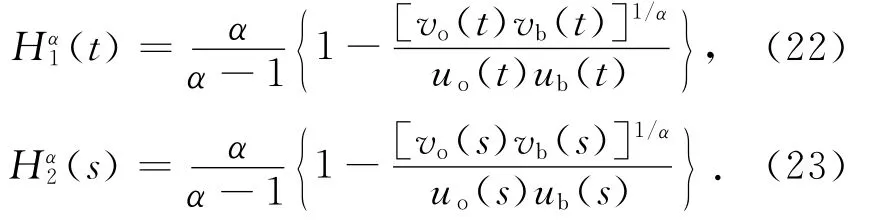
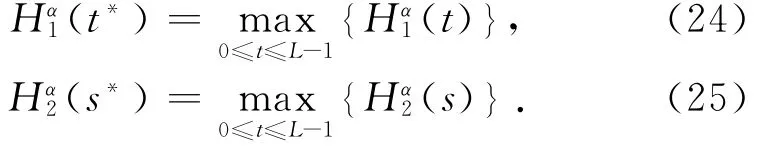
假设区域2和3中像素出现的概率为0,可得
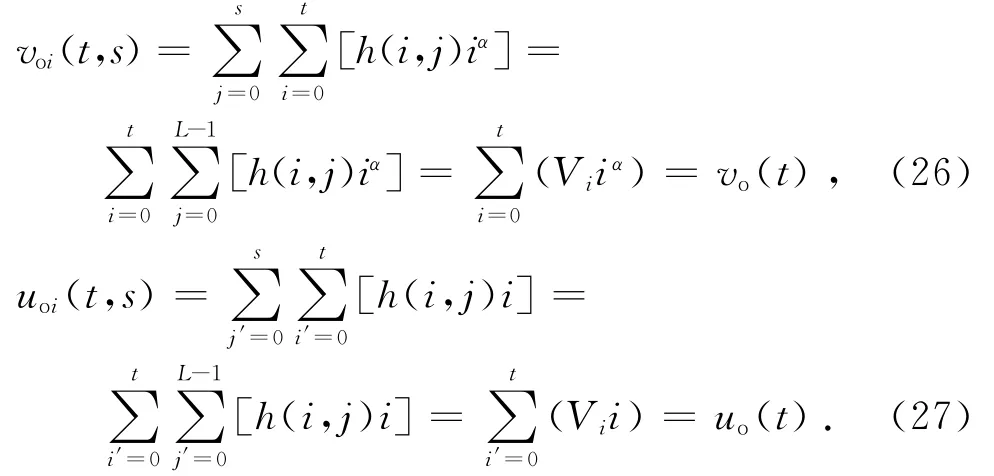
同理可得

由此,二维Arimoto灰度熵阈值法的准则函数φ(t,s)可转化为如下形式:
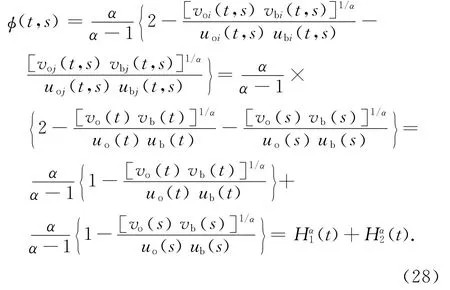
那么,二维最佳阈值(t*,s*)满足
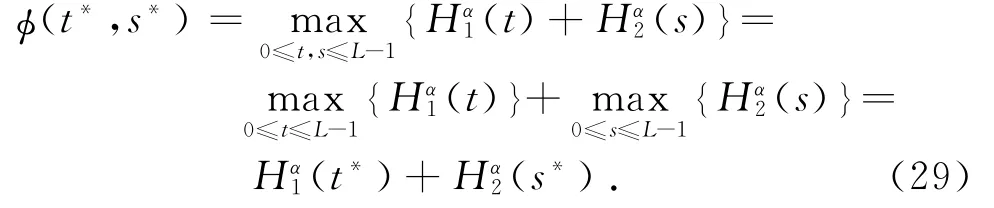
式(25)证明原始灰度图像和邻域平均灰度图像的2个一维Arimoto灰度熵最佳阈值可组合成二维Arimoto灰度熵方法的二维最佳阈值.二维方法需要在L×L的二维空间中进行搜索阈值,而本文基于分解的分割方法转化为在2个长为L的一维空间中搜寻阈值,因此计算复杂度从O(L2)降为O(L).该方法的实质是先对原始灰度图像求取一维Arimoto灰度熵最佳阈值,以分割目标和背景,再对邻域平均灰度图像选取阈值以滤除噪声.
3 实验结果与分析
利用所提出的基于MABC优化算法或基于分解的二维Arimoto灰度熵方法,对大量不同类型的灰度图像进行分割实验,并与二维Tsallis熵法[7]、二维Tsallis交叉熵法[11]、二维Arimoto熵法[10]的分割结果进行比较.为了加快分割方法的运行速度,同时保证搜索到最佳阈值,实验中利用MABC优化算法对上述3种方法进行优化.所有方法均在Intel(R)Core(TM)2 Duo CPU 2.00 GHz主频/2 GB内存、Matlab2009a环境中运行.以纸张纤维(1 536×2 048)、淡水鱼(362×976)、车牌(255× 320)、狒狒(512×512)4幅图像为例,其中车牌图像加入均值为0,方差为0.01的高斯噪声.图2~5分别为原始图像及采用二维Tsallis熵法、二维Tsallis交叉熵法、二维Arimoto熵法、基于MABC的二维Arimoto灰度熵法、基于分解的二维Arimoto灰度熵法分割后的图像.

图2 纸浆纤维图像的阈值分割结果Fig.2 Thresholding results of pulp fiber image

图3 淡水鱼图像的阈值分割结果Fig.3 Thresholding results of freshwater fish image

图4 车牌图像的阈值分割结果Fig.4 Thresholding results of plate image

图5 拂拂图像的阈值分割结果Fig.5 Thresholding results of baboon image
如图2所示为纸浆纤维图像及其分割结果.利用图像处理技术测量纸浆纤维的形态参数,了解纤维形态对成纸性能的影响,有助于提高纸张质量.阈值分割则是纸浆纤维形态自动测量中的关键步骤,需要完整准确地提取纤维形状.由分割结果可以看出,二维Tsallis熵法及二维Tsallis交叉熵法均丢失了大量目标信息,无法准确地分割出灰度级较高的纤维,说明Tsallis熵的普适性不强.采用二维Arimoto熵法时,图像的细节信息更为丰富,然而仍没有完整地提取出纸浆纤维.当采用本文提出的2种方法时,能准确获取所有目标纤维,且目标和背景的细节最为清晰.如图3所示为淡水鱼图像的分割结果.在自动化水产养殖中,基于计算机视觉技术的淡水鱼自动分类挑拣系统可大大减少劳动力、提高经济效益.为了满足系统对分割实时性的要求,需要对淡水鱼图像进行阈值分割.当采用二维Tsallis熵法时,鱼图像的边界处丢失了一些信息,且边界与背景无法区分,不利于后续的鱼体轮廓提取.当采用二维Tsallis交叉熵法时,能很好地区分鱼体的边界与背景,但是鱼体背部的纹理不够清晰.由于纹理信息是区分鱼种类的重要依据,采用该方法会降低后续淡水鱼的分类精度.在二维Arimoto熵法和本文提出的2种方法的分割结果中,鱼体轮廓清晰,且保留了更多的纹理细节.如图4所示为车牌图像的分割结果.原始车牌图像中含有大量高斯噪声,当采用二维Tsallis熵法和二维Arimoto熵法时,字符“苏A”不够清晰.采用二维Tsallis交叉熵法及本文基于分解的二维Arimoto灰度熵法能完整清晰地分割出车牌字符,但是仍然含有较多噪声.采用基于MABC的二维Arimoto灰度熵法时,进一步滤除了部分噪声,车牌字符更为清晰,因此,该方法拥有更好的抗噪性能.基于分解的二维Arimoto灰度熵法是在假设图像不含噪声的前提下进行的,算法的去噪性能不佳.对于图5中的狒狒图像,采用本文提出的2种方法时,图像中狒狒的细节边缘信息最为丰富,鼻子和胡须清晰可辨.这是由于Arimoto灰度熵不仅依赖于灰度直方图的分布,还考虑了图像目标和背景类内灰度的均匀性,而其余3种分割方法不同程度地丢失了狒狒的细节信息,因此,本文方法的分割性能更优.
本文提出的Arimoto灰度熵阈值法适用于纹理细节丰富的图像,而对于灰度层次较为简单的图像,二维Arimoto熵法的性能更优.
如表1所示为采用上述方法分割4幅图像的最佳阈值(t*,s*)及运行时间tm.分析表1中的数据可以发现,对于图4的含噪待分割图像,本文提出的2种方法的最佳阈值有所区别,而对于其他无噪图像,本文提出的2种方法得到的二维最佳阈值相近.基于MABC的二维Arimoto灰度熵法的运行速度明显高于近年来提出的3种阈值分割方法.基于分解的二维Arimoto灰度熵方法在2个长为L的一维空间上搜索阈值,进一步降低了计算复杂度,缩短了运行时间.分析本文提出的2种分割方法的主观视觉效果和运行时间可知,在无噪声或弱噪声环境下,基于分解和基于MABC的二维Arimoto灰度熵法的分割效果相近,在噪声环境下,基于MABC的二维Arimoto灰度熵法的分割效果更优,而基于分解的二维Arimoto灰度熵法的运行速度更快.

表1 5种方法的最佳分割阈值及运行时间比较Tab.1 Comparison of five methods in optimal thresholds and running time
为了验证所采用的MABC优化算法的有效性,利用图1中的纸浆纤维图像,比较MABC优化算法、ABC优化算法、混沌人工蜂群(chaotic artificial bee colony,CABC)优化算法[18]的搜索性能.如表2所示为针对纸浆纤维图像,采用上述3种优化算法搜索二维Arimoto灰度熵法得到的最佳阈值(t*,s*)、最佳适应度函数值F及运行时间tr.由表2可以看出,ABC优化算法搜索到的最佳适应度函数值最低,说明该优化算法易陷入局部极值.CABC优化算法拥有较高的搜索精度,但在ABC优化算法的基础上对侦察蜂引入了混沌算子,降低了运行速度.MABC优化算法的搜索精度最高,且由于无须侦察蜂在迭代过程中对较劣种群进行重新初始化,所需运行时间最少.

表2 3种优化算法的搜索结果比较Tab.2 Comparison of three optimization methods in searching results
4 结 论
1)Arimoto灰度熵反映了图像目标及背景类内灰度的差异性,Arimoto灰度熵越大,目标类内灰度差异与背景类内灰度差异的和越小,即类内灰度趋于均匀,可改善图像的分割效果.根据Arimoto灰度熵的定义导出的灰度-邻域平均灰度二维Arimoto灰度熵阈值分割方法,可以进一步提高抗噪性能.
2)基于MABC优化算法的二维Arimoto灰度熵方法可以避免每次迭代适应度函数中的冗余计算,大大减少了运算量.
3)基于分解的二维Arimoto灰度熵方法将计算复杂度从O(L2)降低为O(L).
4)与其他方法相比,采用本文方法分割后图像的目标区域更为完整,纹理细节信息更丰富,同时拥有良好的抗噪性能,大幅减少了运行时间.
(References):
[1]吴一全,朱兆达.图像处理中阈值选取方法30年(1962-1992)的进展(二)[J].数据采集与处理,1993,8(4):268- 282.
WU Yi-quan,ZHU Zhao-da.30 years(1962-1992)of the developments in threshold selection methods in image processing(Ⅱ)[J].Journal of Data Acquisition and Processing,1993,8(4):268- 282.
[2]MAHMOUDI L,EL ZAART A.A survey of entropy image thresholding techniques[C]∥2012 2nd International Conference on Advances in Computational Tools for Engineering Applications.Beirut:IEEE,2012:204- 209.
[3]YIN J,WU Y Q,ZHU L.Multi-thresholding based on symmetric Tsallis-cross entropy and particle swarm optimization[J].Advanced Materials Research,2013,760:1457- 1461.
[4]KAPUR J N,SAHOO P K,WONG A K C.A new method for gray-level picture thresholding using the entropy of histogram[J].Computer Vision,Graphics and Image Processing,1985,29(1):273- 285.
[5]BRINK A D.Thresholding of digital images using twodimensional entropies[J].Pattern Recognition,1992,25(8):803- 808.
[6]龚劬,王菲菲,倪麟.基于分解的二维Renyi灰度熵的图像阈值分割[J].计算机工程与应用,2013,49(1):181- 185.
GONG Qu,WANG Fei-fei,NI Lin.Decomposition based two-dimensional thresholding for image using Renyi gray entropy[J].Computer Engineering and Applications,2013,49(1):181- 185.
[7]SAHOO P K,ARORA G.Image thresholding using twodimensional Tsallis-Havrda-Charvát entropy[J].Pattern Recognition Letters,2006,27(6):520- 528.
[8]WANG S,CHUNG F L.Note on the equivalence relationship between Renyi-entropy based and Tsallis-entropy based image thresholding[J].Pattern Recognition Letters,2005,26(14):2309- 2312.
[9]卓问,曹治国,肖阳.基于二维Arimoto熵的阈值分割方法[J].模式识别与人工智能,2009,22(2):208- 213.
ZHUO Wen,CAO Zhi-guo,XIAO Yang.Image thresholding based on two-dimensional Arimoto entropy[J].Pattern Recognition and Artificial Intelligence,2009,22(2):208- 213.
[10]张弘,范九伦.二维Arimoto熵直线型阈值分割法[J].光子学报,2013,42(2):234- 240.
ZHANG Hong,FAN Jiu-lun.Two-dimensional Arimoto entropy linear-type threshold segmentation method[J].Acta Photonica Sinica,2013,42(2):234- 240.
[11]唐英干,邸秋艳,赵立兴,等.基于二维最小Tsallis交叉熵的图像阈值分割方法[J].物理学报,2009,58:9- 15.
TANG Ying-gan,DI Qiu-yan,ZHAO Li-xing,et al.Image thresholding segmentation based on two-dimensional minimum Tsallis-cross entropy[J].Acta Physica Sinica,2009,58:9- 15.
[12]吴一全,吴诗婳,占必超,等.基于改进的二维交叉熵及Tent映射PSO的阈值分割[J].系统工程与电子技术,2012,34(3):603- 609.
WU Yi-quan,WU Shi-hua,ZHAN Bi-chao,et al.Thresholding based on improved two-dimensional cross entropy and Tent-map PSO[J].Systems Engineering and Electronics,2012,34(3):603- 609.
[13]梁建慧,马苗.人工蜂群算法在图像分割中的应用研究[J].计算机工程与应用,2012,48(8):194- 196.
LIANG Jian-hui,MA Miao.Artificial bee colony algorithm based research on image segmentation[J].Computer Engineering and Applications,2012,48(8):194- 196.
[14]KARABOGA D,AKAY B.A comparative study of artificial bee colony algorithm[J].Applied Mathematics and Computation,2009,214(1):108- 132.
[15]GAO W,LIU S.A modified artificial bee colony algorithm[J].Computers and Operations Research,2012,39(3):687- 697.
[16]ZHANG H.One-dimensional Arimoto entropy threshold segmentation method based on parameters optimization[J].Communications in Computer and Information Science,2011,4:573- 581.
[17]吴一全,纪守新.灰度熵和混沌粒子群的图像多阈值选取[J].智能系统学报,2010,5(6):522- 529.
WU Yi-quan,Ji Shou-xin.Multi-threshold selection for an image based on gray entropy and chaotic particle swarm optimization[J].CAAI Transactions on Intelligent Systems,2010,5(6):522- 529.
[18]罗钧,李研.具有混沌搜索策略的蜂群优化算法[J].控制与决策,2010,25(12):1913- 1916.
LUO Jun,LI Yan.Artificial bee colony algorithm with chaotic-search strategy[J].Control and Decision,2010,25(12):1913- 1916.
Two-dimensional Arimoto gray entropy image thresholding based on bee colony optimization or decomposition
WU Yi-quan1,2,3,4,YIN Jun1,ZHU Li1,YUAN Yong-ming2
(1.College of Electronic and Information Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China;2.Key Laboratory of Freshwater Fisheries and Germplasm Resources Utilization,Ministry of Agriculture,Freshwater Fisheries Research Center,Chinese Academy of Fishery Sciences,Wuxi 214081,China;3.Key Laboratory of Fishery Equipment and Engineering,Ministry of Agriculture,Shanghai 200092,China;4.Jiangsu Provincial Key Laboratory of Pulp and Paper Science and Technology,Nanjing 210037,China)
The existing thresholding methods based on Arimoto entropy do not consider the uniformity of gray scale within object cluster and background cluster.A 2D Arimoto gray entropy thresholding method based on bee colony optimization or decomposition was proposed.Arimoto gray entropy was defined and a 2D Arimoto gray entropy thresholding method was derived.The method based on bee colony optimization and another method based on decomposition were adopted to find the optimal thresholds.Fast recursive formulae for the intermediate variables were given using the method based on bee colony optimization.A modified artificial bee colony(MABC)optimization algorithm was adopted to find the optimal threshold of the 2D Arimoto gray entropy method.The redundant computations of fitness function in an iterative procedure could be avoided.Using the method based on decomposition,the computations of 2D Arimoto grayentropy thresholding method were converted into two one-dimensional spaces.The computational complexity was further reduced.The experimental results show that,compared with three similar methods proposed recently,the proposed methods have superior image segmentation performance and a better antinoise performance.In the segmented images,objects are completely kept,and the edges and textures are clear.Moreover,the proposed methods have high running speed and can meet the real-time processing requirement of segmentation in the actual system.
image processing;thresholding;2D Arimoto gray entropy;modified artificial bee colony optimization algorithm;decomposition;fast recursive algorithm
TP 391.41
A
1008- 973X(2015)09- 1625- 09
10.3785/j.issn.1008-973X.2015.09.003
2014- 07- 25. 浙江大学学报(工学版)网址:www.journals.zju.edu.cn/eng
国家自然科学基金资助项目(60872065);农业部淡水渔业与种质资源利用重点实验室开放基金资助项目(KF201313);农业部渔业装备与工程技术重点实验室开放基金资助项目(2013001);江苏省制浆造纸科学与技术重点实验室开放基金资助项目(201313);农业部东海海水健康养殖重点实验室基金资助项目(2013ESHML06);江苏高校优势学科建设工程资助项目(2012);2013年研究生学位论文创新与创优基金资助项目(DZS201203).
吴一全(1963-),男,教授,博导,从事图像处理与分析、目标检测与识别、智能信息处理研究.ORCID:0000-0003-3999-9838.
E-mail:nuaaimage@163.com

