基于多类跟驰行为的车头时距混合分布模型

王福建,戴美伟,孙凌涛,金 盛

（浙江大学建筑工程学院,浙江杭州310058）

基于多类跟驰行为的车头时距混合分布模型

王福建,戴美伟,孙凌涛,金 盛

（浙江大学建筑工程学院,浙江杭州310058）

基于实际的驾驶行为特性,将驾驶员的驾驶状态分为强跟驰、弱跟驰和自由流3种状态,建立能够描述这3种状态的车头时距三元混合分布模型.利用北京快速路实测数据,通过最大期望（EM）算法标定了三元混合分布模型中的参数,对3种不同驾驶行为数据进行分析.通过研究对比各个车头时距分布模型的拟合精度,结果表明,提出的车头时距混合模型的拟合结果优于威布尔分布以及对数正态分布模型.

交通流；分布模型；最大期望算法；车头时距；跟驰

车头时距指是连续两辆车头部或尾部通过同一断面的时间间隔,它是计算通行能力、优化信号配时、构建车辆跟驰模型的核心参数,是通行能力评估、驾驶特性分析、交通安全评价的重要依据,在实践中有广泛的应用价值.通过对车头时距数据的研究可以计算交叉口的通行能力［1-3］,分析车辆的跟驰特性、换道特性、快速路出入口匝道运行效率等.

国内外学者针对城市道路、高速公路和城市快速路的车头时距分布特性进行了大量的研究,得到了威布尔分布［4］、移位负指数分布［5］、爱尔朗分布［6］、对数正态分布［7］、二分分布、M3分布［8］等多种车头时距分布模型.

负指数分布和移位负指数分布适用于车辆随机到达的情况.由于道路特性、交通信号等因素的制约,城市道路交通流到达往往不是随机的,城市交通流的复杂性使得单一的分布模型很难很好地解释车头时距的分布规律.陶鹏飞等［9］在前人研究的基础上,将车辆行驶状态分为跟驰和自由流2种状态,提出车头时距的混合分布模型.通过最大期望（expectation maximization,EM）算法对相关参数进行标定,结合参数结果对路段上、下游的车头时距统计特征的差异值进行分析.但是研究中跟驰状态下车头时距服从正态分布的假设缺乏实测数据的验证［9］.本文通过对跟驰状态下车头时距数据的定量分析,构建了强弱跟驰条件下的车头时距混合高斯模型；结合自由流状态下的分布模型,构建车头时距的三元混合分布模型.

1 驾驶状态分析与数据采集

1.1 驾驶状态分析

在实际跟驰行为过程中,不同驾驶员保持的车头时距会有差别,同一驾驶员保持的车头时距在不同交通环境下也不同.根据驾驶员性格特点的不同,可以将驾驶员分为谨慎型和激进型两类.谨慎型驾驶员倾向保持较大的车头时距,激进型驾驶员倾向保持较小的车头时距.Ohta［10］的驾驶行为实验证实了上述结论,即不同驾驶员会选择不同的车头跟驰车头时距.根据不同的情况,驾驶员的跟驰行为分成两种状态.第一种是强跟驰状态,在这种状态下,后车驾驶员与前车保持较短的车头时距,根据前车的速度变化调整自己的驾驶行为.第二种是弱跟驰状态,在弱跟驰状态下,后车驾驶员没有紧紧跟随前车,在强跟驰状态车头时距基础上增加一定的心理裕值,为自己预留更充足的时间来应对前车的速度变化.因此,前车微小的速度变化不会影响后车的驾驶行为［11］.基于上述思想,本文通过驾驶员在车辆运行过程中的驾驶行为特性分析,将车辆的运行状态分为强跟驰、弱跟驰、自由流三种状态,建立三元混合分布模型,并进行参数标定与实际验证.

为了进一步验证强跟驰和弱跟驰存在的合理性,需要分离出处于跟驰状态的车辆数据,因此对跟驰状态和自由流状态的车辆进行判定.在跟驰状态下,前后两辆车的车头时距较小,后车驾驶行为受到前车的影响,驾驶员根据前车的速度变化调整驾驶行为.

在小样本的驾驶实验中,已有研究发现驾驶员保持的强跟驰车头时距分布与弱跟驰车头时距分布呈现以均值为中心左右对称的情况［12］.本文假设强跟驰状态下车头时距、弱跟驰状态下车头时距均服从正态分布,采用高斯混合模型来拟合该特性.美国《道路通行能力手册》（HCM）规定,当车头时距小于或等于5 s时,车辆处于跟驰状态［13］,本文采用这一标准对数据进行筛选.

1.2 数据采集

选取北京北三环快速路四通桥至联想桥路段采集数据进行验证.分别在快速路入口匝道上游、入口匝道下游、出口匝道下游3处进行采集,以验证不同地点对车头时距特性的影响.采集路段有内、中、外三条车道,分别独立采集各自车道的车头时距数据.在采集到同一条车道内车辆通过检测带时刻的基础上,通过简单相减得到车头时距数据.数据采集时间为2012年6月24日6：30～8：30,包含了不同交通状态下的车头时距数据.主要采集的数据包括车头时距、车速、车辆类型、流量、时间占有率等,具体采集地点和检测位置如图1所示.

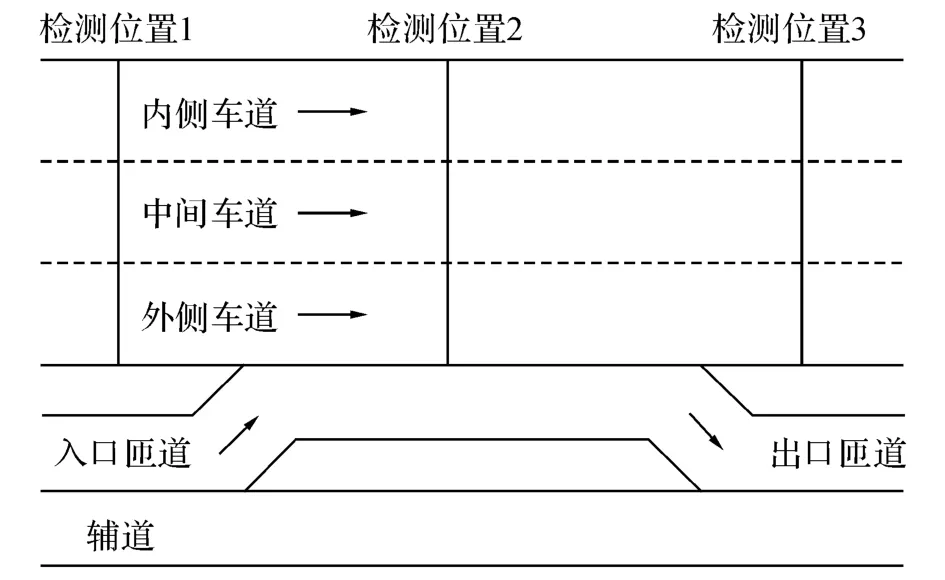
图1 采集地点位置Fig.1 Survey sites

2 跟驰车头时距分布模型

2.1 高斯混合分布模型

高斯混合分布模型是单一高斯分布函数的延伸,有限高斯混合模型可以逼近任意的概率密度分布,因此,近年来被广泛应用在语音、图像识别、车辆类型区分［14］、交通状态判别［15］等方面,取得不错的效果.本文将高斯混合模型应用到快速路跟驰状态下的车头时距分布分析中,结合实际调查数据,对提出的两类跟驰特性假设进行验证.

在实际跟驰过程中,驾驶员保持的车头时距会有差别.假设跟驰状态中存在n种状态车头时距分布,对于跟驰状态下车头时距的高斯混合分布模型,可以用下式表示：

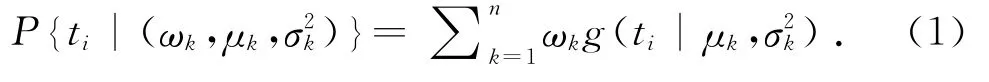
式中：P｛ ti｜（ωk,μk,） ｝为多个单高斯分布的组合,即高斯混合分布模型；n为单高斯模型的个数；ti为第i辆车和第i＋1辆车之间的车头时距；ωk（k＝1,…,n）为各混合成分的先验概率,表示第k类车头时距分布占总体样本的比例1；g（ti｜μk,σk）为第k类高斯分布的概率密度函数,用下式表示：

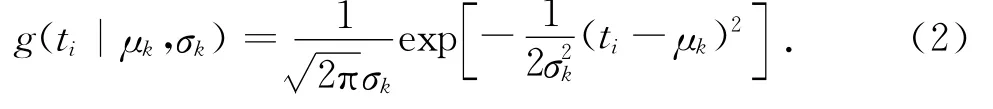
其中,μk分别为第k类高斯分布的均值和方差.

2.2 参数估计模型

对于高斯混合分布模型参数的求解,若直接对参数求导,则得到的方程组比较复杂,不易求解.对于这类问题,常采用EM算法进行求解.EM算法是依赖于无法观测的隐藏变量,在概率模型中寻求参数的最大似然估计方法.随着EM算法的发展,EM算法已经成为解决高斯混合分布模型问题的主要算法.

最大期望算法一般需要2个步骤交替进行计算.

1）计算期望E.根据初始化的参数值或前一次迭代的模型参数结果来计算隐藏变量的后验概率,即隐藏变量的期望.

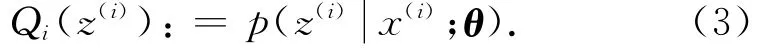
2）最大化M.最大化步骤是指在计算期望E步基础上求得隐藏变量的期望值.

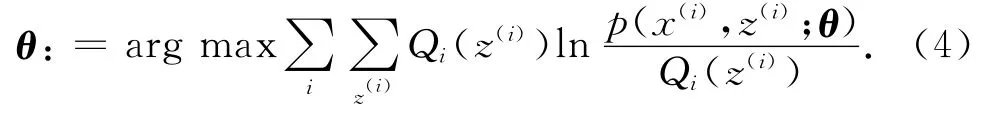
通过M步计算的参数估计值用于下一个E步中,不断迭代,直到收敛.本文的EM算法具体流程如下.

1）初始化高斯混合分布模型的参数.

2）E步骤：根据步骤1）得到的模型参数,估计未知参数的期望值,给出当前的参数估计.对于第i个车头时距样本数据ti,ti由第k类高斯分布生成的概率为

3）M步骤：对于得到每个车头时距样本数据的ti,它的p（i,k）ti是由第k类高斯分布决定的.假设有m个数据样本.在估计第k类高斯分布模型参数时,采用最大似然的方法对式（5）进行求解,求出参数值为

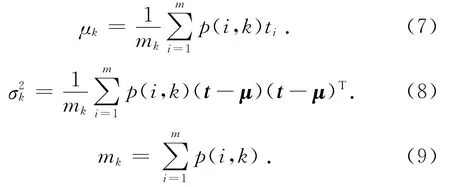
式中：t＝［t1,t2,…,tm］,μ＝［μ1,μ2,…,μn］.

4）若同时满足｜ωk－1－ωk｜≤εω,｜μk－1－μk｜≤εμ,｜σk－1－σk｜≤εσ,则表示收敛,停止迭代,得到参数的最大似然估计值；否则返回2）继续进行迭代计算.

针对小于5 s的车头时距数据进行分析,应用EM算法对参数进行估计.采用柯尔莫哥洛夫-斯米尔诺夫检验（K-S检验）对数据结果进行检验.K-S检验的p-value值表示在原假设为真的条件下样本观察结果出现的概率.若p很小,则表示原假设情况的发生概率很小,根据小概率原理可知,能够拒绝原假设.p越小,拒绝原假设的依据越充分.一般来说,p大于0.05,可以接受原假设.根据p值结果,能够推断总体是否服从某一分布.

本文检验原假设H0：数据总体样本符合高斯混合分布.若p大于显著性水平α（0.05）,则接受H0；否则拒绝H0.

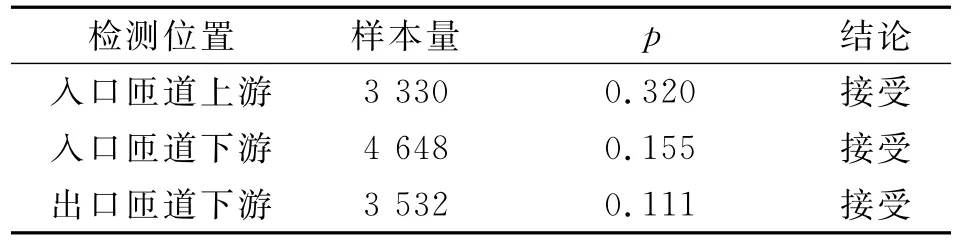
表1 高斯混合分布检验结果Tab.1 Test results of Gaussian mixture model

如表1所示,3个地点的车头时距数据K-S检验的p值均大于0.05,都能够通过显著性水平0.05假设检验.3个地点跟驰状态车头时距t分布拟合结果如图2～4所示.结果表明,在跟驰状态下车头时距数据能够使用2个高斯分布的混合分布进行拟合,进一步验证了强跟驰和弱跟驰状态存在的合理性.

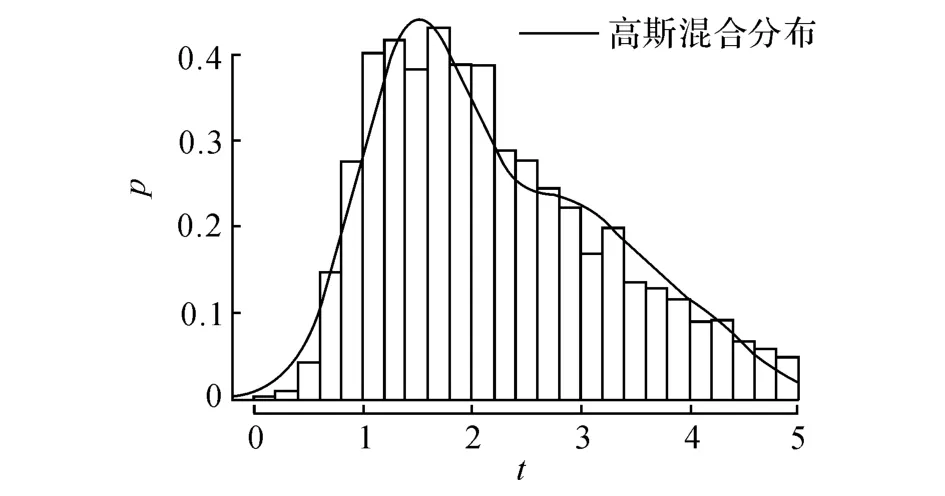
图2 入口匝道上游跟驰状态车头时距分布图Fig.2 Headway distribution of car-following status at upstream on-ramp

3 车头时距混合分布模型

3.1 模型建立

基于上述的分析结果可知,跟驰状态下车头时距分布规律和自由流状态不同.在跟驰状态下,后车跟随前车行驶并受到前车的制约,前车状态的改变会引起后车的状态变化,车头时距在一定范围内变化.根据驾驶行为特性的不同,跟驰状态分为强跟驰和弱跟驰两类,车头时距服从高斯混合分布.在自由流状态下,后车驾驶行为不受到前车的影响,车头时距的变化范围较大.根据文献［16］可知,自由流状态的车头时距服从负指数分布.本文将车流运行状态归为强跟驰、弱跟驰和自由流三种状态,建立描述总体中具有不同特性数据的混合分布模型.车头时距混合分布模型为

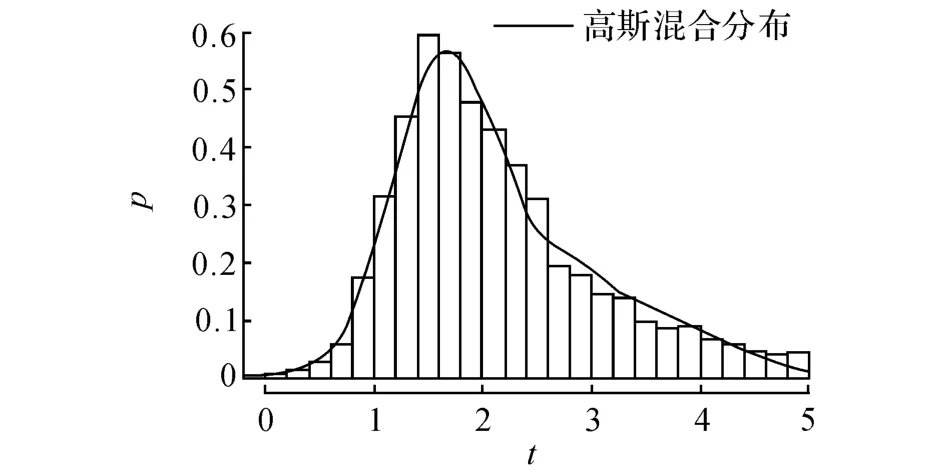
图3 入口匝道下游跟驰状态车头时距分布图Fig.3 Headway distribution of car-following status at downstream on-ramp

图4 出口匝道下游跟驰状态车头时距分布图Fig.4 Headway distribution of car-following status at downstream off-ramp

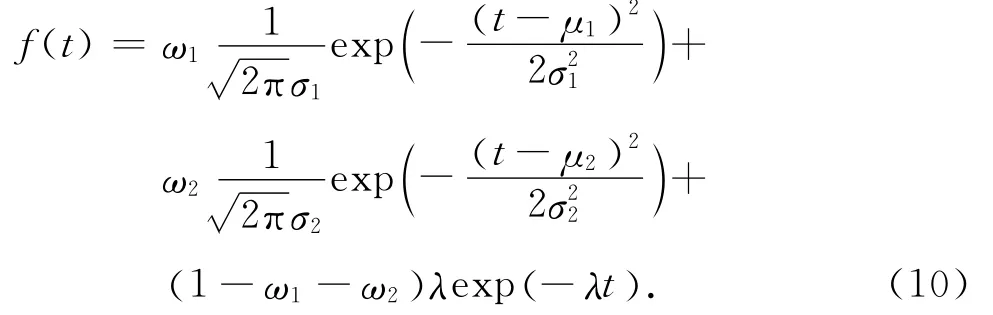
式中：f（t）为车头时距概率密度函数；ω1为弱跟驰状态样本数据占总样本的比例；ω2为强跟驰状态样本数据占总样本的比例；μ1、μ2为两类高斯分布期望值,数值上分别等于弱跟驰状态和强跟驰状态下出现频率最高的车头时距；σ1、σ2为两类高斯分布的标准差,分别表示弱跟驰状态和强跟驰状态下车头时距相对期望值μ1、μ2的离散程度；λ为自由流状态的车辆到达率.

3.2 参数估计

对于本文提出的混合分布模型,直接采用一般极大似然估计方法不易求解,采用EM算法进行参数求解.

对于总体样本参数,记

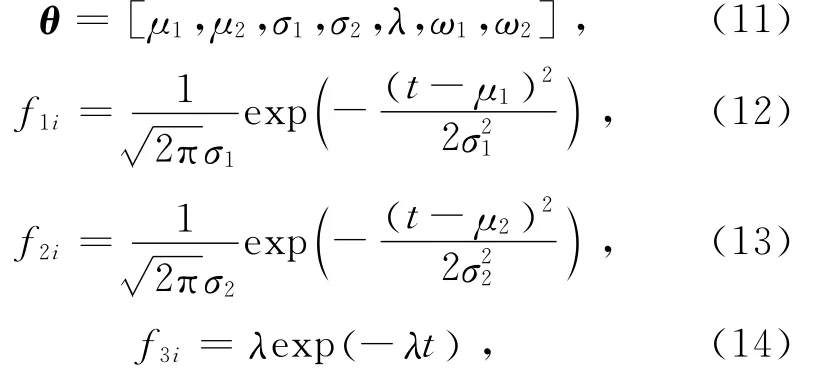
则三元混合分布的表达式为

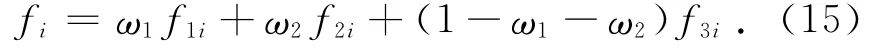
对于ti服从三元混合分布,设Ii为示性变量（i＝1,2,3）.由于无法直接判断ti来自f1i、f2i、f3i中的哪个集合,Ii（i＝1,2,3）为不可观测的随机变量.

ti和Ii的联合概率分布为g（ti,Ii,θ）＝（ω1f1i）I1（ω2f2i）I2（（1－ω1－ω2）f3i）I3,从而Ii在ti确定时的条件概率分布为

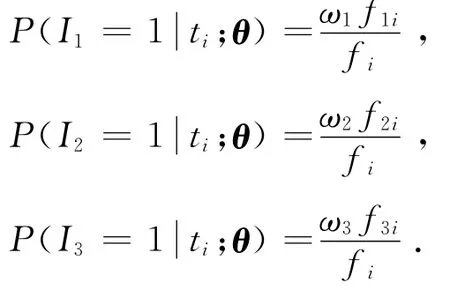
给定初始值θ（0）,EM算法的步骤如下.

1）（E步骤）计算期望为

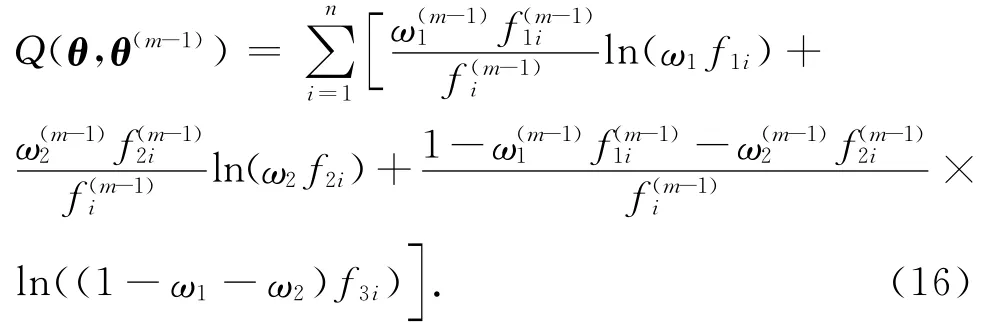
2）（M步骤）最大化.

通过求解∂Q（θ（m）,θ（m－1））／∂θ＝0,使Q（θ（m）, θ（m－1））＝max Q（θ（m）,θ（m－1））.7个未知数有7个迭代方程.设

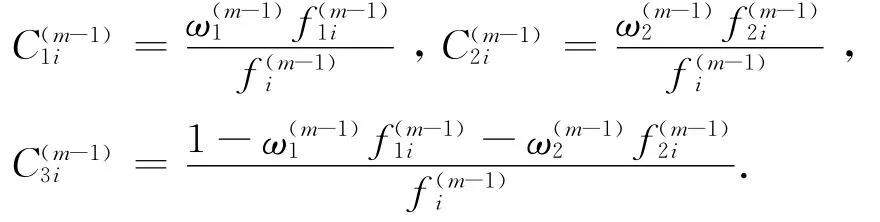
迭代方程式如下：

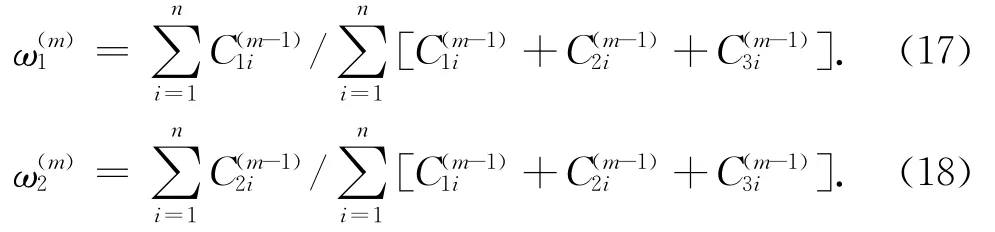
3）以θ（m）作为θ（m－1）的更新值,重复E步和M步,当｜｜θ（m）－θ（m－1）｜｜小于某个给定的临界值时停止迭代.

4 实例验证

利用北京快速路采集的数据,应用EM算法进行参数标定,具体结果如表2所示.原假设是总体样本符合本文建立的模型分布,显著性水平为0.05.p＞0.05表示接受原假设,反之表示拒绝.

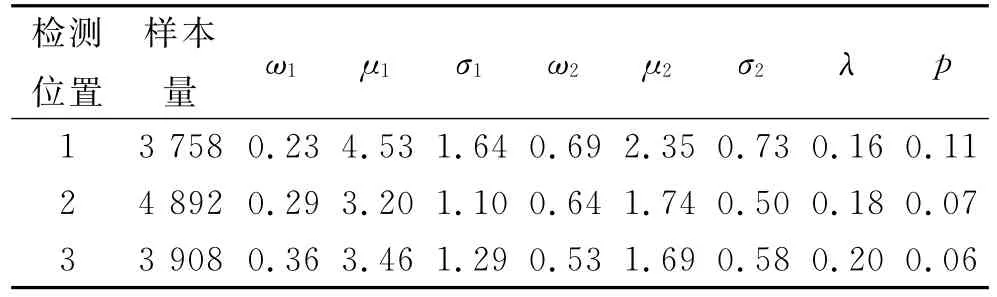
表2 三元混合分布模型参数标定结果Tab.2 Parameter calibration results of ternary mixture distribution model

表2的结果显示,3个检测位置的车头时距数据均通过K-S检验,进一步验证了该模型的合理性.μ1表示弱跟驰状态下驾驶员期望达到的车头时距.μ2表示强跟驰状态下驾驶员期望达到的车头时距.μ2也是驾驶员维持驾驶安全的最小车头时距.当车头时距小于μ2时,驾驶员能够明显感受到驾驶风险急剧增大,脑力负荷明显增加.μ1－μ2代表驾驶员从弱跟驰状态转变到强跟驰状态所需的心理裕值,它能够为驾驶员提供一定的反应时间来应对前车的速度变化.不同检测位置的心理裕值不同.入口匝道下游,心理裕值μ1－μ2较其他两个位置小,这是因为在入口匝道下游车流量最多,前、后车之间保持的距离相对较短,所以驾驶员从强跟驰状态转换到弱跟驰状态的时间相对较短.

比较不同检测位置的μ1和μ2.入口匝道上游的车头时距比入口匝道下游和出口匝道下游的车头时距大.这是由于在入口匝道上游,车流量相对较少,车头时距相对较大.在入口匝道下游和出口匝道下游,受到汇入和驶离主线车辆的影响,车流量较多且车辆交织严重,车头时距相对较小.

（1－ω1－ω2）表示自由流状态下车辆所占总体样本的比例.比较不同检测位置的（1－ω1－ω2）的结果可以发现,入口匝道下游自由流的比例最小.这是由于汇入车流的影响,车流量增大,车辆行驶受到制约,自由流比例下降.入口匝道上游和出口匝道下游自由流比例较大,这是由于这两个检测位置的车流量较少,车辆行驶自由程度较大.

σ1和σ2表示跟驰状态下车头时距相对期望车头时距μ1和μ2的偏离程度.对比入口匝道下游和出口匝道下游,虽然强跟驰、弱跟驰的车头时距比较接近,但是车辆在匝道分流之后,在出口匝道下游的车辆会有不同程度的加速,车队离散现象增加.在出口匝道下游的σ1和σ2会大于入口匝道下游.

λ表示自由流车辆的到达率,在入口匝道下游,虽然自由流比例较小,但是由于汇入车辆增加,使自由流车辆到达率增大.因此,入口匝道下游较入口匝道上游的自由流车辆到达率有所增加.

5 模型对比

应用本文模型、二元混合分布模型、对数正态分布模型、威布尔分布模型对实测数据进行拟合、检验,并对比模型效果.

利用极大似然估计的方法计算威布尔分布模型和对数正态分布模型的待定参数,参数标定结果如表3所示.拟合结果采用K-S检验方法进行检验,结果见表4.

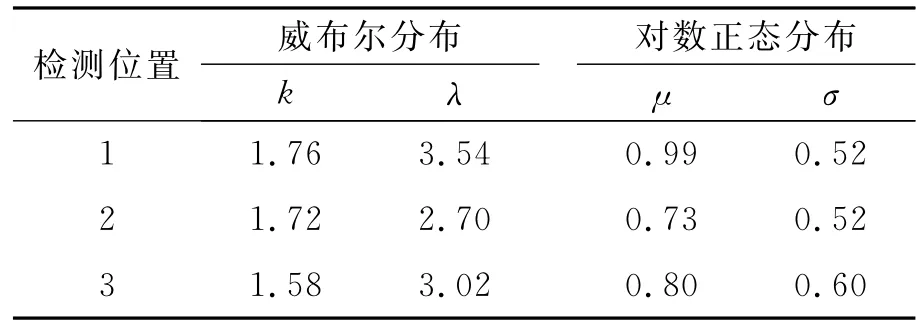
表3 分布模型参数取值Tab.3 Value of distribution model parameters

表4 各个分布模型检验结果Tab.4 Test results of all distribution models

对比各个模型的拟合曲线结果如图5～7所示.

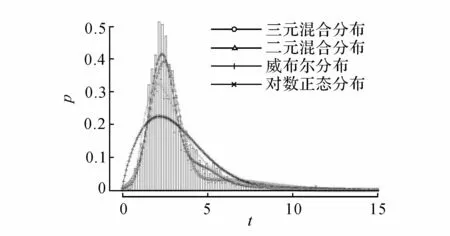
图5 入口匝道上游车头时距分布模型拟合效果对比Fig.5 Comparison of fitting effect of all headway distribution models at upstream on-ramp

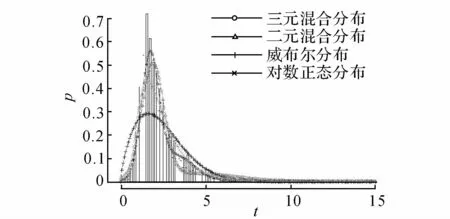
图6 入口匝道下游车头时距分布模型效果对比Fig.6 Comparison of fitting effect of all headway distribution models at downstream on-ramp

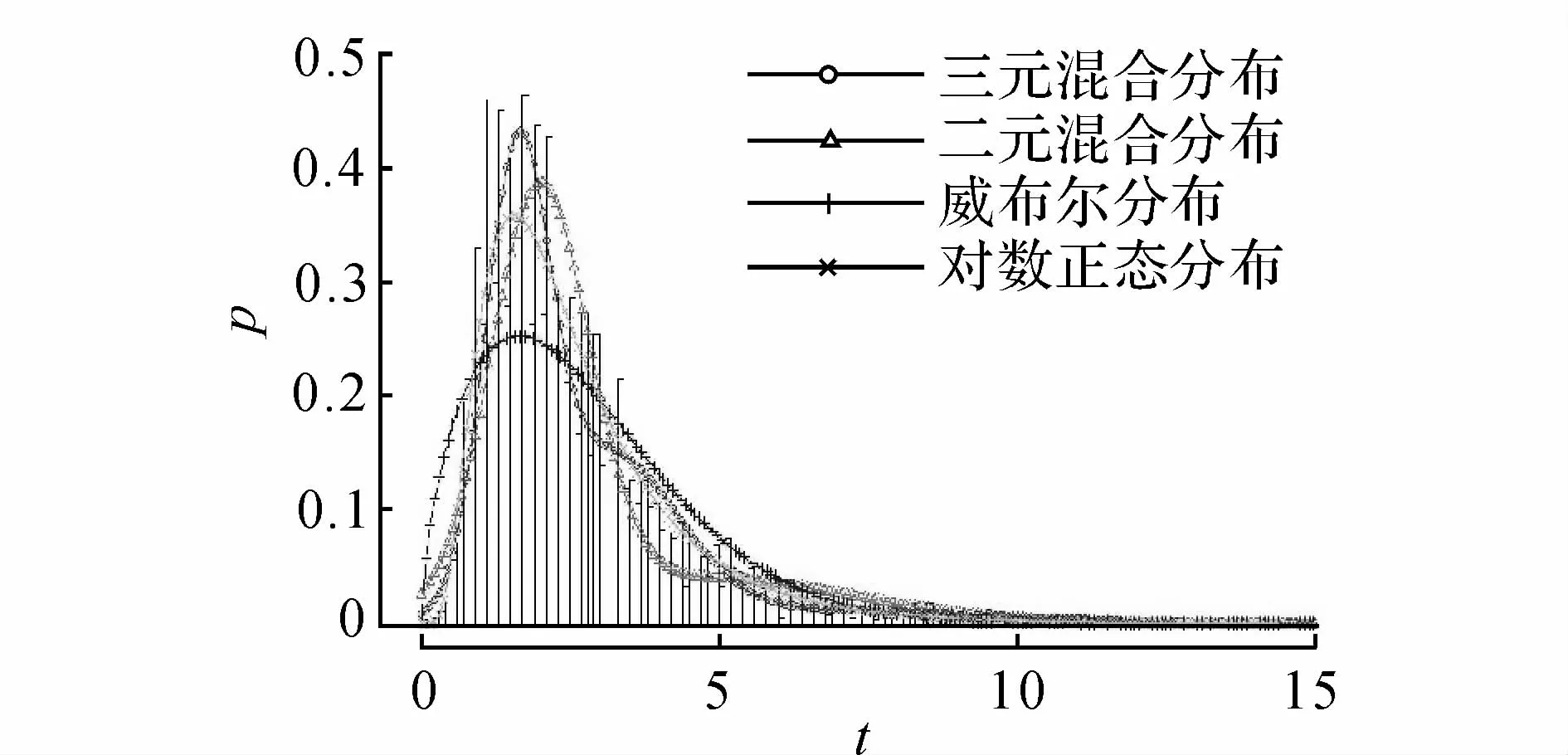
图7 出口匝道下游车头时距分布模型效果对比Fig.7 Comparison of fitting effect of all headway distribution models at downstream off-ramp

对比表4的K-S检验结果可知,仅三元混合分布模型通过检验,二元混合分布、威布尔分布、对数正态分布均无法通过.从图5～7的曲线拟合结果可以看出,三元混合分布模型拟合的曲线最接近实测数据分布,其他模型拟合曲线与实测数据偏差较大.由此可见,实测数据能够用本文建立的分布模型较好地拟合,验证了本文提出的理论框架的合理性.根据驾驶员的不同特性,车辆运行状态可以分为强跟驰、弱跟驰、自由流三种状态.两个高斯分布分别代表强跟驰和弱跟驰状态下的车头时距分布,负指数分布代表自由流状态下的车头时距分布.

6 结 语

本文考虑到驾驶员驾驶心理,将车辆的运行状态分为强跟驰、弱跟驰、自由流3种状态,建立三元混合分布模型描述车头时距分布规律.利用实测快速路数据验证模型,通过参数估计确定相关参数,验证了强跟驰和弱跟驰状态存在的合理性.在强跟驰状态下,后车驾驶员与前车保持较短的车头时距,根据前车的速度变化调整自己的驾驶行为.在弱跟驰状态下,后车驾驶员没有紧紧跟随前车,而是保持较长的车头时距,为自己预留更充足的时间来应对前车的速度变化.本文进一步对比分析三元混合分布模型、二元混合分布模型、对数正态分布模型、威布尔分布模型的拟合效果.结果表明,三元混合分布模型对车头时距分布规律的拟合效果明显优于二元混合分布模型、对数正态分布模型、威布尔分布模型.研究成果可以为交通状态评价、通行能力分析提供理论基础.其中,强跟驰和弱跟驰状态期望车头时距的标定,有助于分析驾驶员的跟驰行为,深入了解驾驶员车头时距的选择特性,对交通安全的提升具有重要的指导意义.

［1］GARTNER N H,MESSER C,RATHI A K.Monograph on traffic flow theory［M］.Washington：The Federal Highway Administration（FHWA）,1996.

［2］JIN S,QU X,XU C,et al.Dynamic characteristics of traffic flow with consideration of pedestrians'roadcrossing behavior［J］.Physica A,2013,392（18）：3881 -3890.

［3］NAGATANI T.Chaos and headway distribution of shuttle buses that pass each other freely［J］.Physica A,2003,323：686- 694.

［4］姚荣涵,王殿海,李丽丽.机动车车头时距分布的韦布尔修正模型［J］.吉林大学学报：工学版,2009,39（2）：331- 335.

YAO Rong-han,WANG Dian-hai,LI Li-li.Revised Weibull revision model of headway distribution for motor-vehicle［J］.Journal of Jilin University：Engineering and Technology Edition,2009,39（2）：331- 335.

［5］刘江,吕津燕,荣建,等.车头时距分布模型及其在山区双车道公路的应用 ［J］.交通运输工程与信息学报, 2004,2（4）：16- 22.

LIU Jiang,LV Jin-yan,RONG Jian,et al.Headway distribution models and their application on two-lane highway in mountainous areas［J］.Journal of Transportation Engineering and Information,2004,2（4）：16- 22.

［6］DAWSON R F,CHIMINI L A.The hyperlang probability distribution：a generalized traffic headway model［J］.Highway Research Record,1968,244（230）：1- 14.

［7］TOLLE J E.The lognormal headway distribution model［J］.Traffic Engineering and Control,1971,13（1）：22- 24.

［8］COWAN R J.Useful headway models［J］.Transportation Research,1975,9：371- 375.

［9］陶鹏飞,王殿海,金盛.车头时距混合分布模型［J］.西南交通大学学报,2011,46（4）：633- 637.

TAO Peng-fei,WANG Dian-hai,JIN Sheng.Mixed distribution model of vehicle headway［J］.Journal of Southwest Jiaotong University,2011,46（4）：633- 637.

［10］OHTA H.Distance headway behavior between vehicles from the viewpoint of proxemics［J］.IATSS Research, 1994,18（2）：6- 14.

［11］孟凡兴,张良,张伟.驾驶员车头时距研究［J］.工业工程管理,2013,18（2）：131- 135.

MENG Fan-xing,ZHANG Liang,ZHANG Wei.A study on drivers'time headway［J］.Industrial Engineering and Management,2013,18（2）：131- 135.

［12］TAIEB-MAIMON M,SHINAR D.Minimum and comfortable driving headways：reality versus perception［J］.Human Factors,2001,43（1）：159- 172.

［13］TRB,Highway capacity manual.Special Report 209, 3th ed.［C］//Transportation Research Board.Washington：National research Council,1994.

［14］徐程.基于高斯混合模型的车辆自由流速度分布 ［J］.公路交通科技,2012,29（8）：132- 135.

XU Cheng.Distribution of vehicle free flow speeds based on Gaussian mixture model［J］.Journal of Highway and Transportation Research and Development, 2012,29（8）：132- 135.

［15］刘曙云,关积珍,李元左.基于高斯混合模型的道路交通状态特征辨识方法［J］.中南林业科技大学学报, 2009,29（2）：151- 155.

LIU Shu-yun,GUAN Ji-zhen,LI Yuan-zuo.Method for identification of roadway traffic characteristics based on Gaussian mixture models［J］.Journal of Central South University of Forestry and Technology,2009, 29（2）：151- 155.

［16］王殿海.交通流理论［M］.北京：人民交通出版社, 2002：13- 19.

Mixed distribution model of vehicle headway based on multiclass car following

WANG Fu-jian,DAI Mei-wei,SUN Ling-tao,JIN Sheng
（College of Civil Engineering and Architecture,Zhejiang University,Hangzhou 310058,China）

Based on the characteristics of driver's psychological behavior,driving behaviors were classified into strong car-following,weak car-following and free driving state.Then a ternary mixed distribution model that can describe the headway distribution of three driving states was built.The parameters of the ternary mixture distribution model were determined by expectation maximization（EM）algorithm through a case study of Beijing expressway,and the data of three different driving behavior were deep analyzed.Results show that the fitting precision of ternary mixed distribution model is the best compared with other Weibull and Lognormal models.

traffic flow；distribution model；expectation maximization algorithm；headway；car following

10.3785／j.issn.1008-973X.2015.07.013

U 491

A

1008- 973X（2015）07- 1288- 07

2014- 04- 15. 浙江大学学报(工学版)网址：www.journals.zju.edu.cn／eng

国家自然科学基金资助项目（51278455,51208462,61304191）；浙江省重点科技创新团队资助项目（2013TD09）.

王福建（1969－）,男,副教授,从事交通控制的研究.E-mail：ciewfj＠zju.edu.cn

金盛,男,讲师.ORCID：0000-0001-6110-0783.E-mail：jinsheng＠zju.edu.cn