基于NURBS曲面敏感点的曲面检测测点优化

赖金涛,傅建中,沈洪垚,甘文峰

（浙江大学机械工程学院,浙江杭州310027）

基于NURBS曲面敏感点的曲面检测测点优化

赖金涛,傅建中,沈洪垚,甘文峰

（浙江大学机械工程学院,浙江杭州310027）

基于NURBS曲面控制点重构的加工误差在机测量方法,提出测点优化选择方法.通过对NURBS曲面进行分析,将曲面上控制点影响最强点和曲面极值点定义为曲面的敏感点,利用曲面敏感点的在机测量数据对NURBS曲面控制点进行重构,得到拟合加工曲面.比较加工曲面和设计曲面可以得到曲面的加工误差,对曲面的加工精度进行评估,指导曲面的误差补偿.实验过程对一自由曲面进行实际加工,通过在机测量和三坐标测量得到曲面的加工误差,分别利用均布法、等参数法和敏感点法对测点进行选择,得到相应的拟合加工曲面.分析结果表明,采用提出的测点优化选择方法获得的加工曲面具有更好的拟合精度.

NURBS曲面；控制点重构；测点优化；在机测量

自由曲面在零件设计中越来越广泛的应用对自由曲面的精密化制造提出了更高的要求.国内外很多学者对如何测量和补偿自由曲面的加工误差进行了研究,与一般规则零件的加工误差不同,自由曲面的加工误差在曲面范围内是不同的,因而对自由曲面的加工误差进行测量和评估变得非常困难.高精度的自由曲面加工一般包括如下步骤.在数控机床上加工自由曲面,然后将加工后的零件转移到三坐标测量机上对曲面上的一系列离散点进行测量,用测量得到的点云数据插值得到加工曲面［1］,通过比较加工曲面和设计曲面得到曲面的加工误差分布；最后根据得到的误差分布进行误差补偿加工,达到提高自由曲面加工精度的目的.

对自由曲面的测量主要有2个要求：测量的精度和测量的效率；主要影响因素包括测量的方法、测点的选择和曲面的重建方法.曲面的测量方法分为接触式测量和非接触测量［2］.测量点的数量和分布直接影响到测量过程的效率,如何在保证一定测量精度的情况下选择合适的测点数量和分布至关重要.郑惠江［3］提出一种针对STL模型数据文件格式特点的自然二次曲面特征参数提取方法和基于三角形折叠的复杂曲面离散数据检测点布局策略.Ainsworth等［4］提出在自由曲面参数空间uv方向上均匀采样的方法.Elkott等［5］提出基于等参数化、等面积和等平均曲率的测点选择方法,可以有效地选择自由曲面检测的测点.Li等［6］采用B样条对自由曲面进行建模,利用费雪信息矩阵的统计分析方法对测量点进行优化选择,提高了曲面测量的效率.Woo等［7］研究了Halton-Zaremba序列采样方法在自由曲面测量中的应用.Obeidat等［8］对自由曲面的分区测点规划进行研究,提出3种针对自由曲面的采样点选择算法.陈浪等［9］提出以物体重心坐标为数学模型的采样算法,保存了曲面拓扑信息和网格自组功能,为自由曲面的坐标测量提供了简洁高效的途径.

通过三坐标测量机进行自由曲面零件测量需要将工件从机床上转移到三坐标测量机上重新进行装夹定位,因而得到的测量数据需要和设计曲面进行配准［10］.在进行补偿加工时,需要再次将工件转移到机床上,这不仅会引入重定位误差,而且在机床和测量机间来回转移会耗费大量的辅助时间.在机测量技术的出现很好地解决了该问题,Chen等［11］使用在机测量方法对自由曲面上的529个点进行测量,拟合出了加工的曲面.然而,在机测量对测量的效率提出了更高的要求,低效率的测量过程大大降低了机床的加工效率.Cho等［12］根据预测的切削误差对测点的数量和分布进行优化,提高了在机测量的效率.王益等［13］提出基于NURBS曲面控制点重构的加工误差在机测量方法,能够快速地获取自由曲面加工误差,并对曲面的面轮廓度误差进行评定.基于等参数的测点选择虽然可以满足测量的精度要求,但是冗余的测点会降低测量效率,需要对测量进行优化选择.

本文基于NURBS曲面控制点重构的加工误差在机测量方法,提出一种测点优化选择方法.将曲面上控制点影响最强点和曲面极值点定义为曲面的敏感点,通过对敏感点的测量来获取自由曲面的加工误差,提高了曲面误差测量的效率.

1 测量原理介绍

从NURBS曲面的定义（见式（1））可以看出,曲面由控制点、权因子和节点向量确定,其中任意参数的变动都会引起曲面的形状发生改变.本文提出一种基于NURBS曲面控制点重构的加工误差在机测量方法,可以通过对加工曲面上一系列点的实际坐标值来获取曲面加工误差.利用在机测量系统对曲面上一系列离散点进行测量,得到曲面测点位置实际加工的坐标；然后根据测点坐标对设计曲面控制点进行重构,获得加工曲面；最后根据加工曲面和设计曲面,计算出曲面的加工误差.

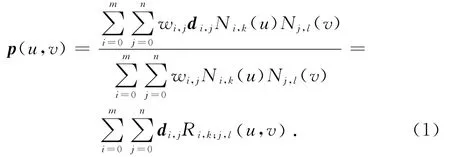
式中：

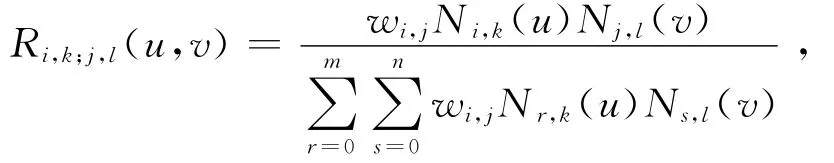
k和l分别为曲面uv方向的次数,di,j（i＝0,1,2,…,m；j＝0,1,2,…,n）为曲面的控制顶点,wi,j为与控制顶点di,j相联系的权因子,Ni,k（u）和Nj,l（v）分别为曲面u方向k次和v方向l次的B样条基函数.

设p为k×l次NURBS曲面上参数为u（ue≤u＜ue＋1）和v（vf≤v＜vf＋1）的一点,对应的控制顶点为di,j,p点调整后通过q（x,y,z）点（见图1）,新的控制顶点为.由于p点的位置同时受到很多个控制顶点的影响,需要同时调整p点对应的控制顶点di,j（i＝e－k,e－k＋1,…,e；j＝f－l,f－l＋1,…,f）.根据设计曲面和加工曲面在采样点处的差异对设计曲面的控制点进行迭代重构,将迭代后满足设定的拟合精度err的曲面作为加工曲面,di,j每次迭代量εi,j通过下式［13］计算：

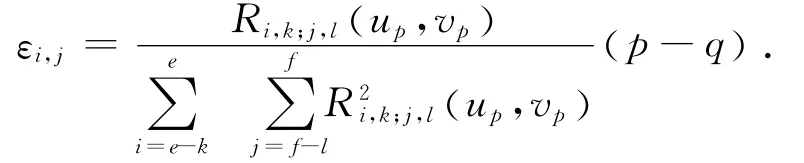
图1 设计曲面和加工曲面Fig.1 Designed surface and machined surface

2 曲面敏感点

通过对曲面上一系列点的测量可以实现对NURBS曲面加工误差的测量,测量点的数量和分布直接影响了曲面加工误差测量的效率和精度.一般情况下,测量点的选择方法有均布法和等参数法,曲面加工误差的测量精度会随着曲面2个方向上等分数n的增大而提高.显然,测量点的数量会以n2的速度增长,这会大大降低整个测量过程的效率.根据本文采用的基于NURBS曲面控制点重构加工误差在机测量方法的基本原理,将NURBS曲面上控制点影响最强点和曲面极值点定义为两类曲面敏感点,并将曲面敏感点作为在机测量的测量点.

2.1 控制点影响最强点

NURBS曲面的所有控制点共同影响整个曲面,每一个控制点都有自己的影响区域,影响区域的范围由曲面的次数、节点向量和控制点决定.如图2所示,一张3×3次NURBS曲面,控制点为di,j（i＝0,1,2,…,6；j＝0,1,2,…,6）,每个控制点对曲面都有自己的贡献,图中阴影区域为控制点d2,2的影响区域,所有控制点对曲面的贡献叠加后得到最终的曲面.当图2所示曲面只有控制点d2,2在z向对曲面产生贡献时,曲面的形状如图3所示,曲面上的最高点为该控制点对曲面影响最强点.

NURBS曲面的控制点和节点向量存在对应的关系,但不是一一对应的.一般来说,在计算某一uv参数下曲面上的点时,首先会根据uv参数在节点向量中的序号确定对计算点有贡献的控制点,然后利用与控制点对应的节点向量来计算uv方向的基函数值,最终代入曲面的定义式计算出曲面上与参数空间中uv对应的三维坐标中的点.图4标识了3次NURBS曲面控制点与节点向量的对应关系.设t0～t10为曲面某一方向的节点,d0～d6为对应的一组控制点,控制点d0的影响区域为t0～t4,控制点d1的影响区域为t1～t5,以此类推.在某一控制点的影响区域内,区域内存在一个影响最强点.

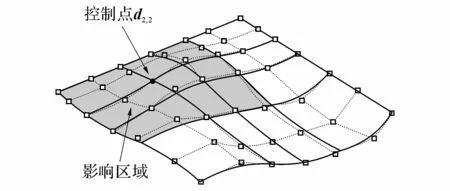
图2 NURBS曲面及控制点d 2,2的影响区域Fig.2 NURBS surface and influence area of d 2,2

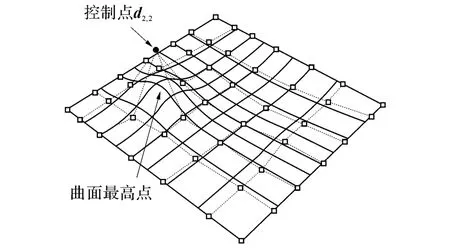
图3 z向单控制点作用下曲面形状Fig.3 Surface shape with single control point

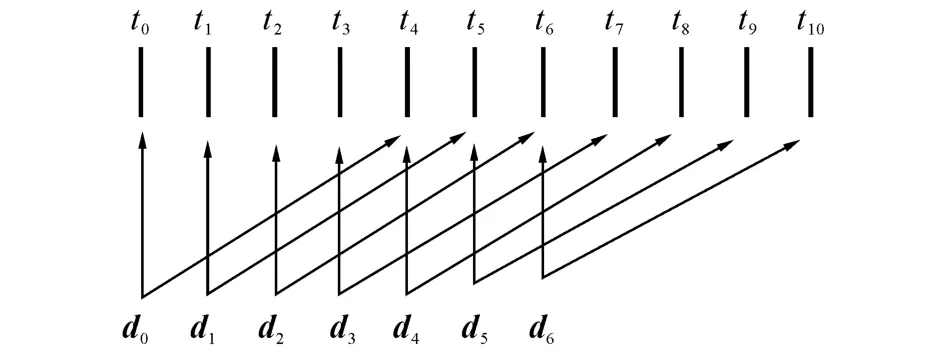
图4 控制点与节点向量的对应关系Fig.4 Relation between control points and knot vector

将式（1）分解为

当z向只有一个控制点di,j产生的贡献不为0时,

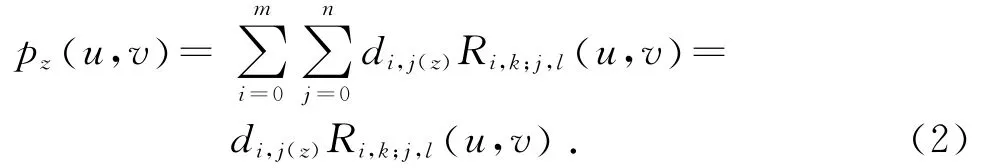
图3所示的曲面只有d2,2对曲面产生贡献,代入式（2）可得,

根据曲面的节点向量可以计算出R2,3；2,3（u,v）在参数域中的分布,结果如图5所示,分布的变化趋势和图3中曲面的形状一致.R2,3；2,3（u,v）对曲面的影响在u＝0.282 5,v＝0.288 5时最强,并在远离该点处迅速衰减,在影响区域外部为0.

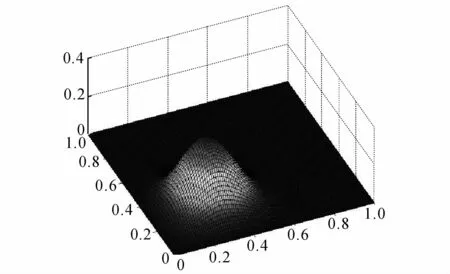
图5 参数域中R 2,3；2,3（ u ,v）的分布Fig.5 Distribution of R 2,3；2,3（ u ,v） in parametric domain

通过比较控制点影响最强点的实测值和理论值,可以直接决定该控制点的调整方向,因为该控制点对这一坐标具有主导影响.将曲面控制点影响最强点定义为曲面的敏感点,可以通过计算节点向量各节点处对应的型值点得到.

2.2 极值点

由于曲面控制点对曲面的影响区域的重叠性,曲面上的极值不一定出现在节点向量节点处,将曲面极值点作为敏感点用来驱动调整设计曲面,可以保证加工曲面的极值信息.NURBS曲面的极值包含局部极大值和极小值,通常复杂的曲面会同时存在多个极大值和多个极小值.

为了精确地找到曲面上所有的极值点,采用粗略查找和精确定位相结合的方法.粗略查找过程将整个曲面在参数空间内进行均匀离散,计算出各离散参数对应的型值点Pi,j（i＝1,2,…,p；j＝1,2,…,q；p、q分别为曲面在参数空间uv方向上的离散数）.如图6所示,当Pi,j的z坐标同时大于等于与之相邻的4个点时,则Pi,j为曲面上的一个极大值点；若Pi,j的z坐标同时小于等于与之相邻的4个点时,则Pi,j为曲面上的一个极小值点.

粗略查找可以确定出曲面上存在的极大值和极小值的个数及大致的分布,精确定位过程是利用最速下降法确定曲面的极值的准确位置.C1以上连续的曲面在极值点处的一阶导数p′（u,v） 在z方向上为0,可以以此来判断一个点是否为极值点.利用最速下降法求解曲面极值点的程序流程如图7所示.图中,

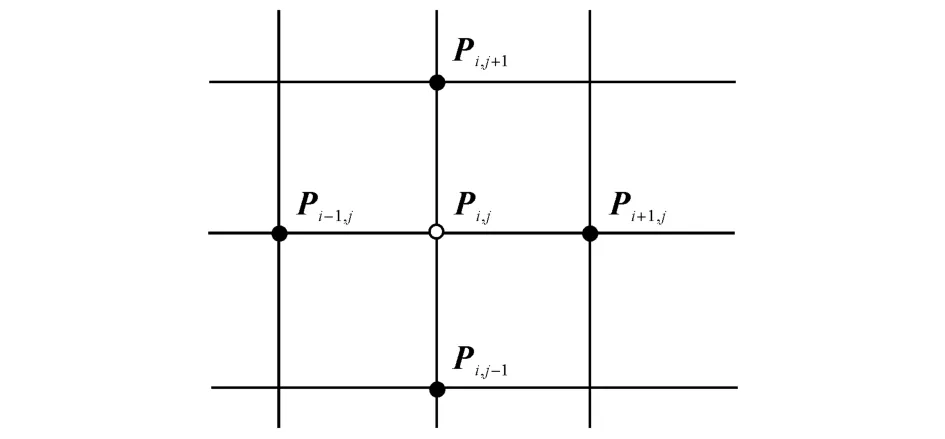
图6 极值判断Fig.6 Extreme point P i,j

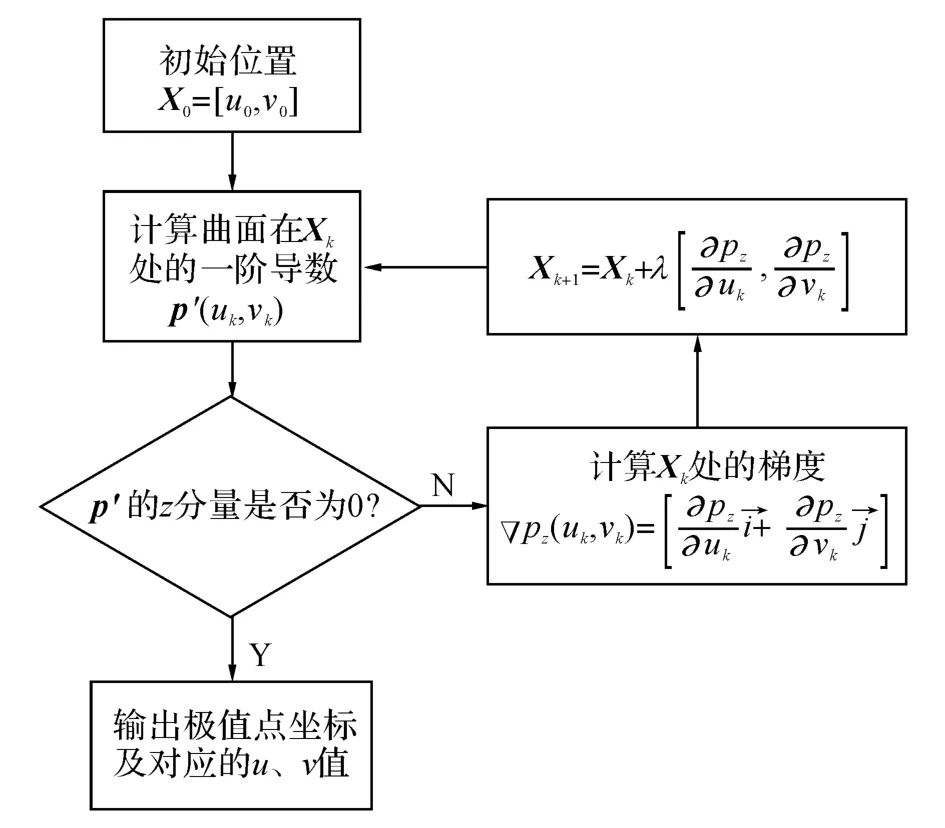
图7 精确定位极值点流程图Fig.7 Flow of determining extreme point

式中：s为设定的迭代步长.

3 实验分析

图8 NURBS实验曲面Fig.8 Experiment NURBS surface

为了验证提出的测点选择方案的有效性,设计了如图8所示的100 mm×100 mm的NURBS实验曲面,节点向量U＝［0,0,0,0,0.264 703,0.5,0.740 06, 1,1,1,1］,V＝［0,0,0,0,0.275 307,0.5,0.753 61,1, 1,1,1］.在MIKRON UCP600五轴立式加工中心上对实验曲面进行加工,利用Renishaw RMP60对加工曲面上根据等参数法选择的120个待测点进行在机测量并记录测量数据（见图9）,120个测量点对应的uv参数如表1所示.

表1 在机测量测点对应的参数值Tab.1 Corresponding parameters of measuring points

图9 在机测量Fig.9 On-machine measurement

利用NURBS曲面控制点重构方法可以根据设计曲面的信息和120个测点的坐标信息得到加工曲面,利用三坐标测量机上对曲面上900个点进行测量（见图10）,并在Rhinoceros软件中对测量点进行拟合得到拟合曲面,结果如图11所示.曲面加工误差通过式（3）计算,根据加工曲面和设计曲面计算出曲面的加工误差如图12（a）所示,通过三坐标测量得到的曲面加工误差如图12（b）所示.可以发现,2种方法下曲面的加工误差在曲面范围内的分布基本一致.

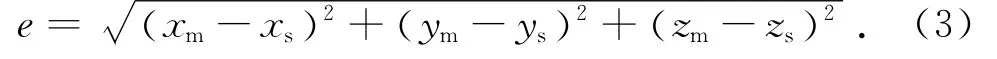
式中：（xm,ym,zm）为加工曲面上的测量点,（xs,ys,zs）为设计曲面上离测点最近的点.

为了验证所提的测点优化选择方法的有效性,对曲面敏感点法、等参数法和均布法测点选择下曲面的重构误差进行比较.由于直接在加工曲面上通过在机测量的方法无法得到精确的参考曲面,将NURBS曲面重构后得到的曲面作为一个参考加工曲面,利用曲面敏感点法在参考加工曲面上进行测量点选择；然后利用均布法和等参数法在等量测量点数的基础上进行测量点选择,其中均布法在笛卡尔坐标系下x向6等分、y向7等分,等参数法在参数空间内u向6等分、v向7等分.表2显示了3种方案下选择的测点位置,对应在曲面上的位置如图13所示.

图10 三坐标测量Fig.10 Coordinate measurement

图11 三坐标测量点曲面拟合Fig.11 Fitting surface from coordinate measurement data

图12 加工曲面法向误差Fig.12 Normal error of machined surface

表2 3种方式下曲面的测点Tab.2 Sampling points in three strategies

计算3种测点选择方案下参考加工曲面上的测点坐标,利用3组测点分别对设计曲面进行重构,设定拟合精度为10－6mm,得到3个加工曲面.比较得到的加工曲面和参考加工曲面可以得到加工曲面的重构误差.为了比较不同测点选择对曲面重构精度的影响,选取u＝0.5、v＝0.5 2条采样线进行拟合误差分析,结果如图14所示.可以看出,2种情况下拟合出的加工曲面和参考加工曲面在采样线处的拟合误差都较小,采用敏感点作为测量点时得到的加工曲面具有更高的拟合精度.曲面的平均拟合误差和最大拟合误差在敏感点法下为2.56×10－5mm和8.78×10－4mm,相比于等参数法的3.17×10－5mm和11.5×10－4mm分别减小了19.2%和23.7%,相比于均布法的2.88×10－5mm和10.5× 10－4mm分别减小了11.1%和16.4%.

图13 实验曲面测点分布Fig.13 Sampling points of experimental surface

4 结 论

（1）本文根据基于NURBS曲面控制点重构的加工误差在机测量的特点,提出一种测量点选择方法.定义曲面上控制点影响最强点和曲面极值点为曲面的敏感点,利用测量曲面敏感点得到的坐标数据重构设计曲面的控制点,得到加工曲面,减少了曲面加工误差测量所需的测点数量,提高了测量的效率.

（2）根据所提的方法设计了相关的实验,通过对曲面上120个点进行测量得到近似的参考加工曲面.通过在机测量方法和三坐标测量方法得到了曲面的加工误差,并且根据均布法、等参数法和敏感点法在参考曲面上选取相应的坐标数据,并得到相应的拟合加工曲面.对得到的拟合曲面进行精度分析.结果表明,采用敏感点法得到的加工曲面平均拟合误差比等参数法和均布法减小了19.2%和11.1%,最大拟合误差比等参数法和均布法减小了23.7%和16.4%.

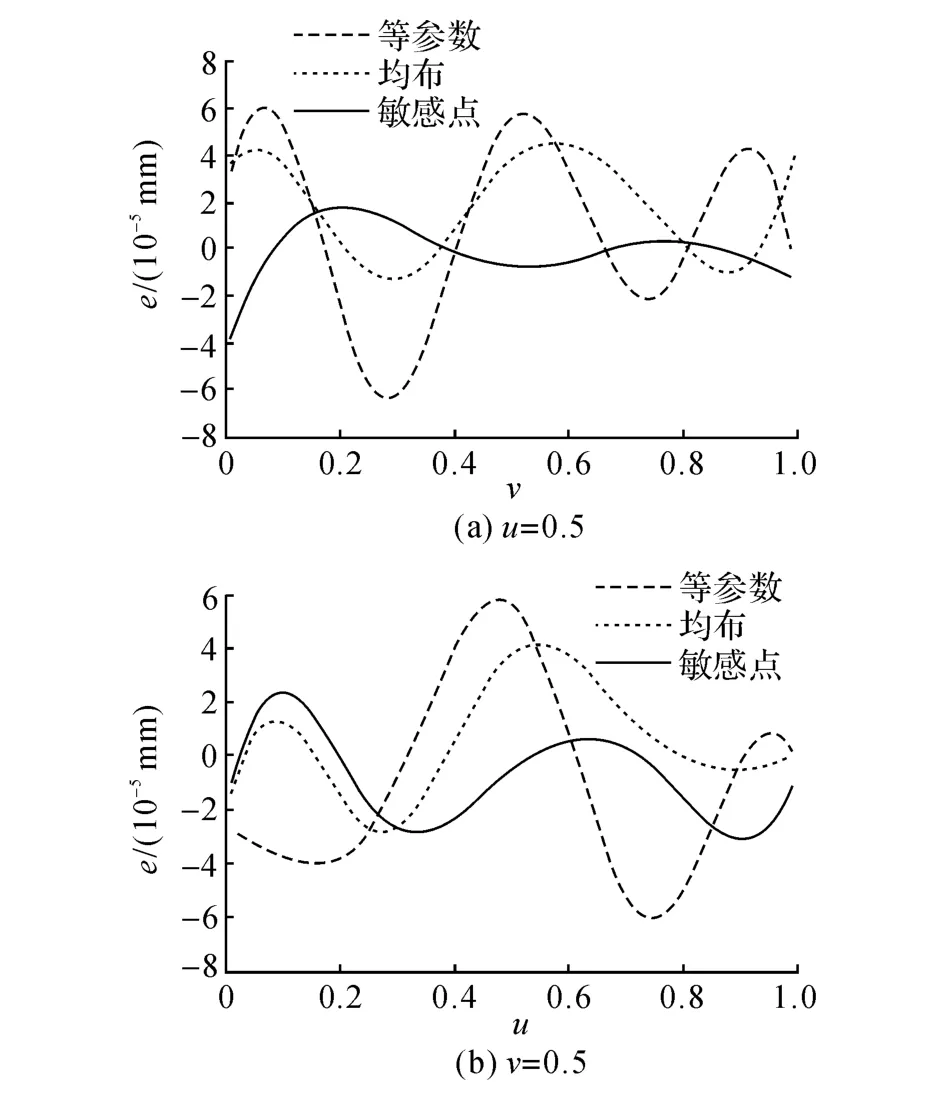
图14 采样线拟合误差Fig.14 Fitting error of sample curve

［1］张学昌,习俊通,严隽琪.基于点云数据的复杂型面数字化检测技术研究［J］.计算机集成制造系统,2005（5）：770- 774.

ZHANG Xue-chang,XI Jun-tong,YAN Juan-qi.Research on digital measurement technology based on point cloud data of complex surfaces［J］.Computer Integrated Manufacturing Systems,2005（5）：770- 774.

［2］LI Y,GU P.Free-form surface inspection techniques state of the art review［J］.Computer-Aided Design, 2004,36（13）：1395- 1417.

［3］郑惠江.在机检测中曲面拓扑特征重建和检测点分布关键技术研究［D］.天津：天津大学,2010：57- 86.

ZHENG Hui-jiang.Research on the key technology of the topological feature reconstruction and sampling point distribution in OMV［D］.Tianjin：Tianjin University, 2010：57- 86.

［4］AINSWORTH I,RISTIC M,BRUJIC D.CAD-based measurement path planning for free-form shapes using contact probes［J］.The International Journal of Advanced Manufacturing Technology,2000,16（1）：23- 31.

［5］ELKOTT D F,ELMARAGHY H A,ELMARAGHY W H.Automatic sampling for CMM inspection planning of free-form surfaces［J］.International Journal of Production Research,2002,40（11）：2653- 2676.

［6］LI Y F,LIU Z G.Method for determining the probing points for efficient measurement and reconstruction of freeform surfaces［J］.Measurement Science and Technology,2003,14（8）：1280- 1288.

［7］WOO T C,LIANG R,HSIEH C C,et al.Efficient sampling for surface measurements［J］.Journal of Manufacturing Systems,1995,14（5）：345- 354.

［8］OBEIDAT S,RAMAN S.An intelligent sampling method for inspecting free-form surfaces［J］.The International Journal of Advanced Manufacturing Technology,2009, 40（11／12）：1125- 1136.

［9］陈浪,秦大同,谢勇.基于坐标测量机的曲面自适应采样的网格生成［J］.重庆大学学报：自然科学版,2001, 24（4）：22- 25.

CHEN Lang,QIN Da-tong,XIE Yong.Study on adaptive sampling and mesh generation of free-form surfaces based on coordinate measuring machine［J］.Journal of Chongqing University：Natural Science Edition,2001, 24（4）：22- 25.

［10］罗琦.基于复合式测头的在机检测数据融合技术研究［D］.大连：大连海事大学,2012：25- 40.

LUO Qi.The study on 3D data registration for surface inspection based on compound probe［D］.Dalian：Dalian Maritime University,2012：25- 40.

［11］CHEN Y,GAO J,DENG H,et al.Spatial statistical analysis and compensation of machining errors for complex surfaces［J］.Precision Engineering,2013,37（1）：203- 212.

［12］CHO M W,SEO T I.Inspection planning strategy for the on-machine measurement process based on CAD／CAM／CAI integration［J］.International Journal of Advanced Manufacturing Technology,2002,19（8）：607- 617.

［13］王益,赖金涛,傅建中,等.基于NURBS曲面控制点重构的加工误差在机测量方法研究［J］.浙江大学学报：工学版,2014,48（10）：1781- 1787.

WANG Yi,LAI Jin-tao,FU Jian-zhong,et al.Research on on-machine measurement of machining error based on reconstruction of NURBS control points［J］.Journal of Zhejiang University：Engineering Science, 2014,48（10）：1781- 1787.

Measuring points optimization in machining error inspection based on reconstruction of NURBS control points driven by sensitive points

LAI Jin-tao,FU Jian-zhong,SHEN Hong-yao,GAN Wen-feng
（College of Mechanical Engineering,Zhejiang University,Hangzhou 310027,China）

A new method to optimize the sampling points of free-form surface was proposed in the surface error inspection based on reconstruction of NURBS control points.The NURBS surface was analyzed,and the points mostly affected by the control points and the extreme points were defined as the sensitive points of the surface.The machined surface was obtained by reconstruction of NURBS control points using the measurement data at the sensitive points.The machining error of the surface can be achieved by calculating the difference between the machined surface and designed surface.Then the accuracy of the surface can be further evaluated and compensated.The experiment was conducted on a NURBS surface and the machining error of the part was achieved both through the on-machine method and the coordinate measurement method.The uniformly distribution method,the equi-parameter method and the proposed method for measuring points selecting were applied to the NURBS surface.Results showed that the machined surface with the sensitive point method had a better fitting accuracy.

NURBS surface；reconstruction of control points；sampling points optimization；on-machine measurement

10.3785／j.issn.1008-973X.2015.07.001

TH 161

A

1008- 973X（2015）07- 1201- 07

2014- 05- 17. 浙江大学学报(工学版)网址：www.journals.zju.edu.cn／eng

国家自然科学基金资助项目（51175461）；高等学校博士学科点专项科研基金资助项目（20120101110055）.

赖金涛（1988－）,男,博士生,从事自由曲面加工误差在机测量的研究.ORCID：0000-0002-6621-0460.E-mail：ljt88＠zju.edu.cn

,傅建中,男,教授,博导.E-mail：fiz＠zju.edu.cn