基于响应面模型的广义空间切削稳定性研究

黄 华,张树有,刘晓健,何再兴

（1.浙江大学流体传动及控制国家重点实验室,浙江杭州310027；2.兰州理工大学机电工程学院,甘肃兰州730050）

基于响应面模型的广义空间切削稳定性研究

黄 华1,2,张树有1,刘晓健1,何再兴1

（1.浙江大学流体传动及控制国家重点实验室,浙江杭州310027；2.兰州理工大学机电工程学院,甘肃兰州730050）

提出以机床立柱和主轴箱不同位置的组合为对象,采用试验设计结合响应面模型的方法研究机床在整个加工空间内的切削稳定性分布规律的方法.选择立柱和主轴箱在移动轨迹上的关键位置的组合作为计算样本点,在ANSYS仿真软件中对样本点的机床动力学特性进行分析.计算每个样本点的最小临界切削深度,建立反映位置特征与最小临界切削深度数值的二次多项式响应面模型,模拟在整个空间内的稳定性切削极限深度近似值,对该响应面模型的质量进行评价.以一台卧式高速加工中心为例,说明了机床立柱位置的变化对切削稳定性有较大影响,为结构和工艺的优化设计提供了理论依据.

切削稳定性；最小临界切削深度；广义加工空间；响应面模型（RSM）

切削加工的不稳定性降低了机械加工的精度,轻则导致高性能机床不能充分发挥其功能,重则导致安全事故发生［1］,因此机床的切削稳定性分析对于切削加工的现场应用或者机床结构优化设计具有极其重要的意义［2］.长期以来,切削稳定性的分析都是以机床某一固定姿态的动力学特性为基础进行［3］,对于一般的铝合金等轻金属的高速加工来说,切削稳定性主要取决于刀具系统的动力学特性［4］,但对于铸铁或者钢材等材料的粗加工、半精加工,切削稳定性主要决定于机床结构本身的动力学特性［5］.该特性随着移动部件位置的变化而不同,因此机床加工位姿的变化对动力学特性有较大的影响.

很多学者研究了机床动静态性能与加工位置变化的关系,如刘海涛等［6］研究广义空间的动刚度,但是相比较而言用户更直接关心的是切削稳定性及极限切削深度.Mohit等［7］研究主轴箱在立柱的顶部、中部、底部位置对切削稳定性的影响,但该机床的立柱是固定的,无法分析立柱的不同位置对切削性能的影响.只研究主轴箱在少数几个极端位置的性能不能全面地反映机床在整个运动空间的特性,但对每个位置都进行有限元分析或者实验,工作量较大.尽管有子结构分析［8］、仿真模型重用［9］等算法,该项工作的计算量仍然很大而难以实施.本文应用试验设计方法,先选取几个典型的立柱和主轴箱的位置组合,然后采用源于统计学的响应面技术（response surface method,RSM）构造在整个运动空间中的最小临界切削深度,最后作出立柱位置、主轴箱位置、稳定性极限切深三者的关系曲线.研究移动部件的位置组合导致的各种加工姿态对切削稳定性的影响,以作为选择切削工艺参数或者机床结构设计改进的依据.

1 广义加工空间切削稳定性建模

在图1所示的切削稳定性叶瓣图中,ap为轴向切削深度,n为主轴转速,水平线表示最小临界切削深度,水平线以下是无条件稳定区,叶瓣内的区域是不稳定切削区,直线和两相邻叶瓣包围的区域是有条件稳定切削区.在以最小临界切削深度以下的深度进行加工时,选择任意转速都不会发生颤振.在一般较硬材料的粗加工、半精加工过程中,选择的转速较低,在图1中对应的“有条件稳定切削区”比较狭窄,所以一般选择在最小临界切削深度以下进行加工.该深度随着立柱、主轴箱等位置的组合而不同.

图1 切削稳定性叶瓣图Fig.1 Cutting stability lobes diagraph

1.1 广义加工空间切削稳定性定义

由切削稳定性分析理论［1］可知,铣削系统的动态切削力可以表示为

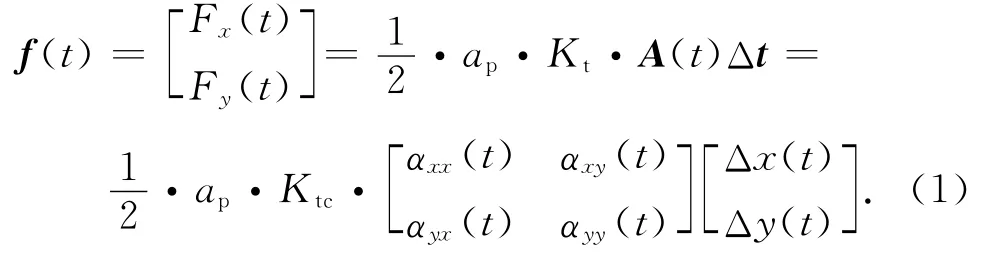
式中：ap为轴向切削深度,Kt为切向切削力系数, A（t）为随时间变化的动态铣削力方向矩阵,Δt为动态切屑的厚度；A（t）为铣削方向力系数,对于特定的工件和刀具材料,它只与刀齿的切入、切出角及切削力系数有关.在频域中求解式（1）的特征方程,并令机床刀尖点的传递函数为

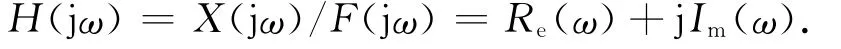
式中：X、F分别为刀尖点的动态位移和切削力.根据文献［3］可知,铣削系统的最小临界切削深度aplim与机床的动力学参数之间存在如下关系：

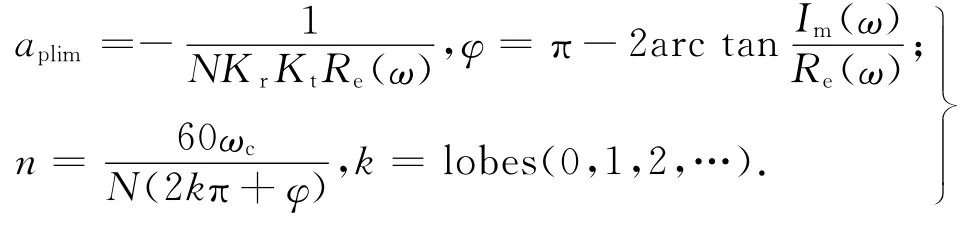
式中：Re和Im分别为刀尖点传递函数的实部和虚部,Kt为切向切削力系数,Kr为径向切削力系数与切向切削力系数的比值,N为刀具齿数,k为稳定性图中的叶瓣数.在多模态系统中存在：

式中：Re（ω）r为系统第r阶模态的频响函数实部,根据振动力学可知,

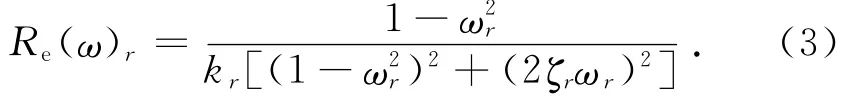
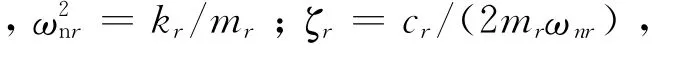
式（4）表明,最小临界切削深度与切削参数、刀具参数和机床的结构参数相关.为了研究结构参数对最小临界切削深度的影响,将切削参数和刀具参数视为常数,则最小临界切削深度仅与刚度kr、固有频率ωnr有关.

令

其中C＝－1／（NKrKt）.因为刚度kr和ωnr是机床的空间位置的函数,令立柱在水平位置的坐标为x,主轴箱在立柱上的位置坐标为y,则

即

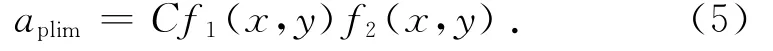
根据式（5）,求出机床在各个不同位置的刚度和频率函数,即可求出在该位置的稳定性切削极限深度.式（5）表达了机床最小临界切削深度在广义加工空间中的变化规律,涵盖了动刚度与固有频率这一动态特性指标,称为广义空间最小临界切削深度函数.

1.2 切削稳定性分析流程

研究立柱和主轴箱综合影响的机床切削稳定性流程,如图2所示.首先根据机床的使用条件,选择某一关键工序,确定工艺参数、切削力系数等参数,以便后续计算稳定性切削极限深度时调用.将CAD模型经适当简化以后导入Ansys中,根据样机的模态实验对相关的结合面参数进行校正,得到精细的有限元模型.根据试验设计理论建立设计样本点,即确定立柱和主轴箱等移动部件在不同位置的组合.为了减少计算工作量,选取几个特殊位置作为样本,采用有限元子结构法计算模态特性.在获得模态参数以后,代入极限稳定性切深公式计算切深.根据多组位置参数和切深参数的组合建立响应面模型,从而获得在整个加工空间内机床的最小临界切削深度,并进一步可以判断该切削深度是否满足生产率的要求.如果不能满足,则需要通过修改工艺参数或者调整机床结构来实现目标.

2 结构模态实验分析及模型校正

建立精确的有限元模型是获得可靠样本点的前提条件,样本点决定了响应面的质量.对作为研究对象的加工中心进行模态实验分析,以作为有限元模型校正的依据.以相同振型的频率误差最小作为目标函数,调整结合面的相关参数,从而得到准确的有限元模型.

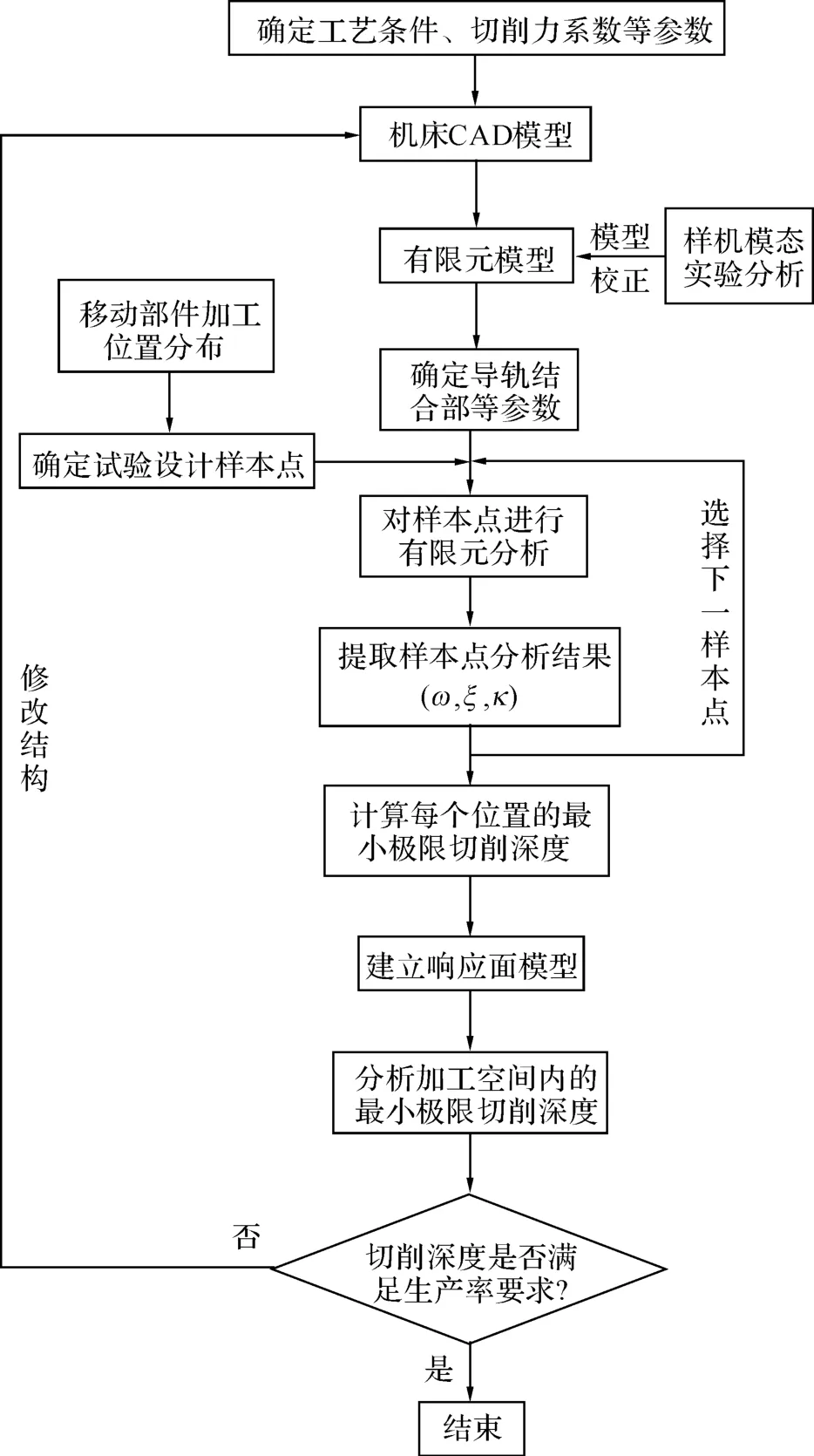
图2 基于响应面的机床切削稳定性分析流程Fig.2 Flow chart of cutting stability analysis based on RSM

2.1 导轨-滑块结合部处理

本文分析的卧式加工中心结构简图如图3所示,主要由床身、立柱、底座、主轴箱、工作台、滑台等零部件组成.床身和底座通过螺栓组固定联接,主轴箱与立柱、立柱与底座、滑台与床身通过导轨滑动连接.

该加工中心存在三对导轨-滑块结合面,相比较而言,立柱与床身之间的导轨-滑块结合面对动力学性能的影响较大,需要对该结合面的参数进行分析.在Ansys有限元建模中,根据力学原理用弹簧-阻尼单元combine14模拟结合面,为了获得弹簧-阻尼单元的刚度、阻尼系数,本文根据赫兹接触理论计算弹簧系统的刚度,根据刚度查表获得阻尼系数［10］,以此为初值在一定范围内进行调整,根据实验结果校正有限元模型.

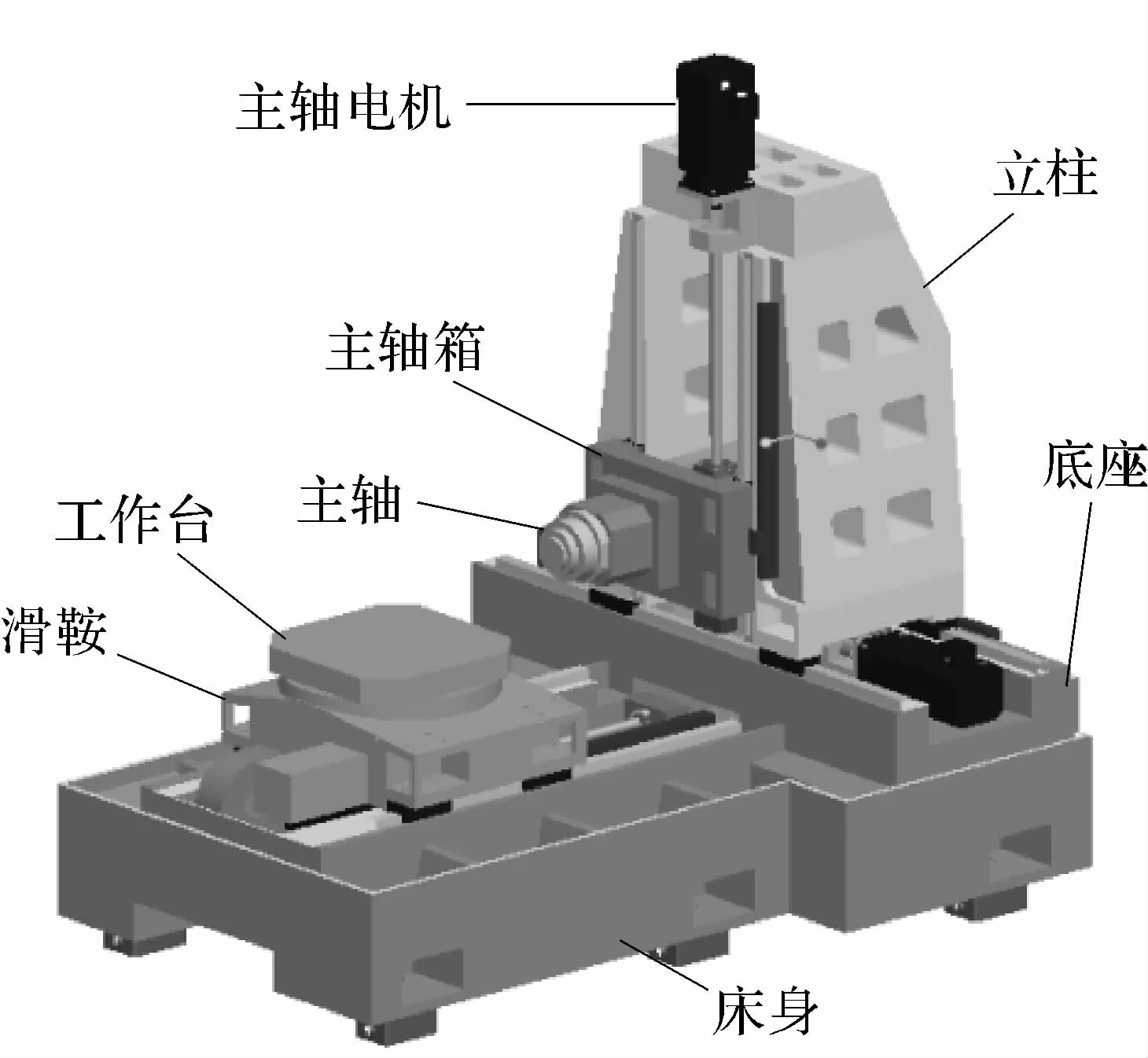
图3 卧式加工中心CAD模型Fig.3 CAD model of horizontal MC

导轨-滑块内力的分布如图4所示.当垂向力Fy作用在滑块上时,单个滚珠的弹性力分别为F1、F2、F3和F4,其中F1＝F2,F3＝F4.

根据图4中的静力平衡条件和文献［11］可知,有如下关系：

式中：m为—单列滚道的接触滚珠数,F0为由预载荷引起的单个滚珠的法向力,Fz为导轨-滑块预载荷,γ为滚珠与滚道面之间的接触角.当已知m、γ、Fy和F0时,可由式（6）、（7）求得F1和F3.根据赫兹接触理论可知,两弹性体由于弹性变形引起的相对位移量［12］为

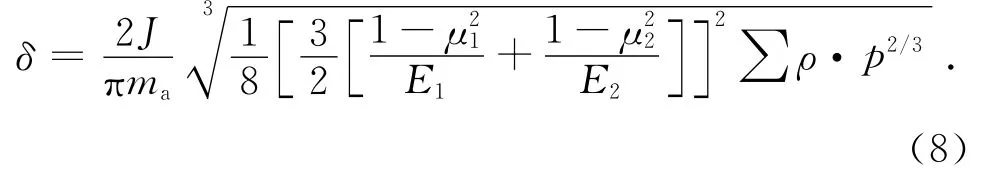
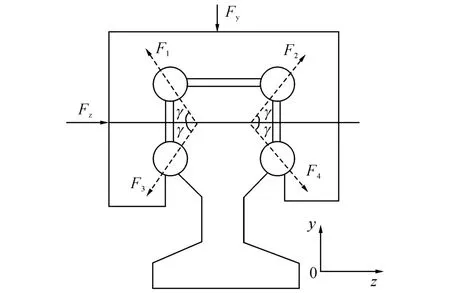
图4 直线滚动导轨的受力分析Fig.4 force analysis of linear rolling guide

式中：p为作用于两弹性体接触点的法向压力,E1、E2为两接触体材料的弹性模量,μ1、μ2为两接触体材料的泊松比,Σρ为两接触体接触点处4个主曲率之和.

对于直线滚动导轨而言,滚珠与滚道面接触处的4个主曲率分别取为

式中：db为单个滚珠直径,f为密合度（滚道曲率半径与滚珠直径之比）,从而可以求得∑ρ＝ρ11＋ρ12＋ρ21＋ρ22.

由式（6）、（7）计算得到导轨滚道内单个滚珠所受的法向力,代入式（8）可得滚珠的变形.单个滚珠受力与变形的关系如图5所示.

由滚珠法向弹性接触变形产生的法向弹性位移量为

由式（6）、（7）和（10）可以分别得到单个滚珠的法向力以及法向变形,再根据图4所示的滚珠在导轨内的受力几何关系,由刚度计算公式可得

式中：Klat、Knor分别为侧向和法向刚度.由此求得单个滚珠产生的弹簧刚度,再根据每个导轨-滑块副内滚珠的个数得到整个导轨-滑块副在x和y方向的弹簧刚度kx、ky,在得到刚度的基础上通过查表获得阻尼系数.

图5 单个滚珠的受力变形图Fig.5 Deformation of single ball

在仿真分析中,对机床底部地脚螺栓的所有自由度施加固定约束,整体采用Solid四面体单元,结合面处的网格进行局部细化以提高模型精确度.对螺栓结合面采用固定接触,导轨-滑块的结合面参数由分析确定,有限元模型和相关的计算参数如图6和表1所示.立柱加主轴箱的质量为2 465 kg,滑块的长×宽×高为65.9 mm×59 mm×22 mm,导轨的宽×高为20 mm×15.5 mm,滚珠直径d0为7.938 mm,每列接触滚珠数为12,接触角α为45°,标准预载荷PP为4.65 k N.

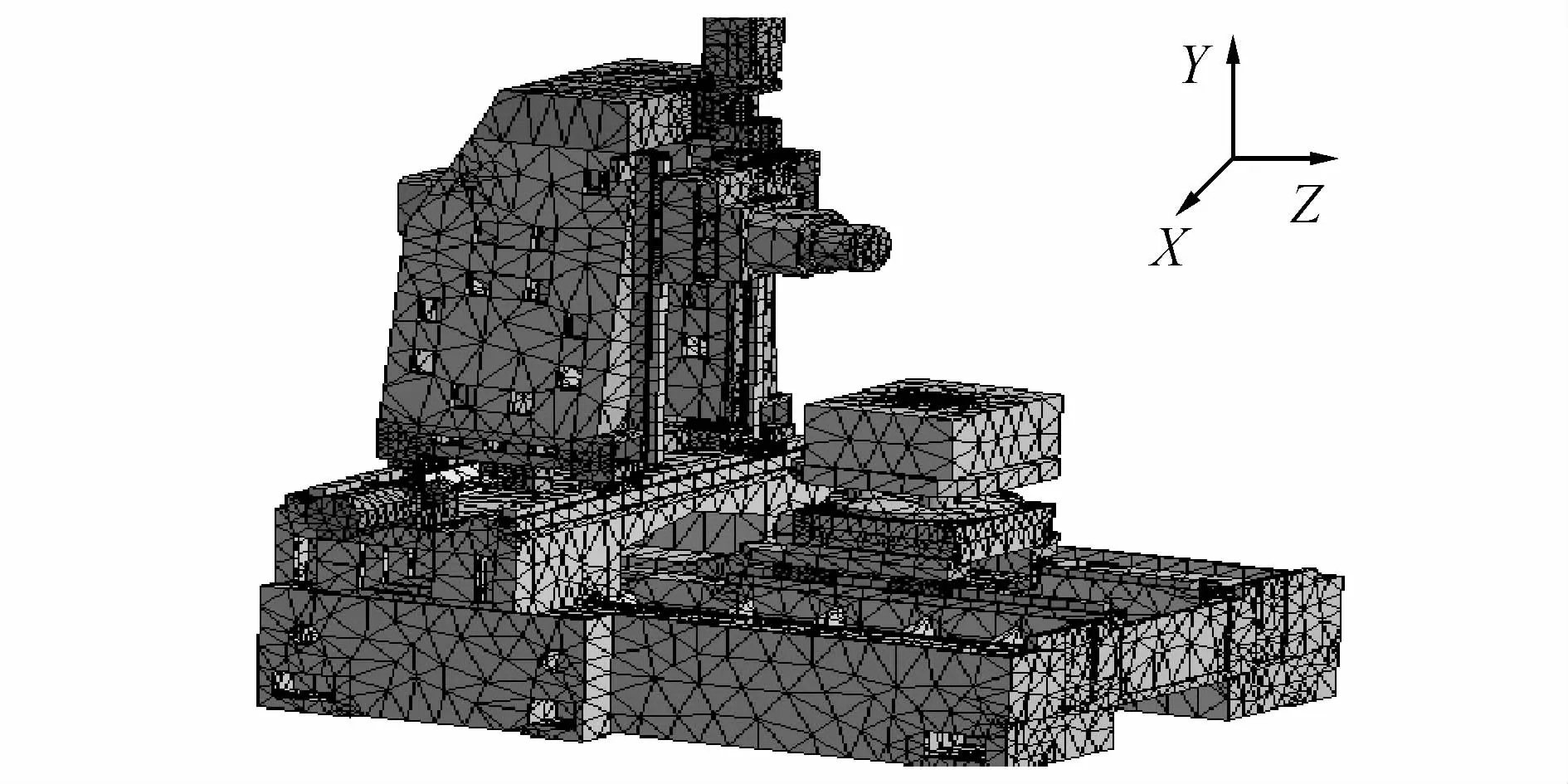
图6 加工中心有限元模型(主轴箱在顶部)Fig.6 Finite element model of MC

表1 机床主要零部件的材料属性和导轨参数Tab.1 Material properties and guide parameters of machine tool main parts

通过理论计算得到ky＝2.2×105N／m3,kz＝5.5×105N／m3,阻尼值分别为cy＝5×105N·s／m3,cz＝4.2×105N·s／m3.该参数作为有限元的弹簧-阻尼单元初值输入.

2.2 结构模态实验分析

某机床企业有一台高速卧式加工中心,采用动柱式结构,该机床的X／Y／Z行程分别为1 500／1 000／650 mm,最高主轴转速为12 000 r／min.对机床进行模态分析和动刚度实验以获得系统动力学特性.如图7所示为机床模型及模态实验的实物照片,表2描述了实验得到的模态频率和振型.

从表2可以看出,机床的前6阶模态中大部分都有立柱参与；低阶模态的动柔度较高,因此立柱是本机床的薄弱环节,立柱对机床的动力学性能有较大影响.在后续的切削稳定性分析中,不能忽略立柱位置变化对整机性能的影响.

2.3 有限元模型修正

相比较而言,固有频率受结合部的刚度影响更大.为了使有限元模型更逼近实际结构的性能,本文通过调整弹簧刚度k来修正有限元模型.由于预载荷大小难于精确控制或者各个滚珠受力不均匀等原因,弹簧刚度可以视作在一定范围内的变量进行调整.比较仿真结果和实验结果的前6阶模态可知,除第5阶振型外,其余5阶振型均相同,因为振型相同的模态才有可比性,以相同振型的前5阶计算频率与实测频率之差的平方和最小为目标函数,以弹簧刚度为设计变量进行优化计算,数学模型如下.

图7 模态实验照片和各测点编号示意图Fig.7 Photos of modal test and measuring point number

表2 机床模态实验结果Tab.2 Results of machine tool modal experiment

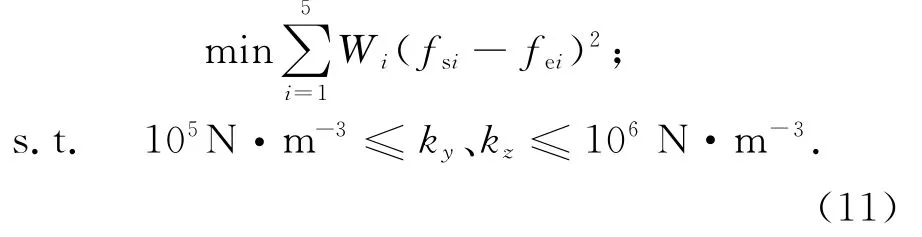
式中：Wi为权重系数,fsi、fei分别为第i阶模态的仿真频率和实验频率.因为低阶频率的影响较大,分别为前5阶频率赋予权重0.3、0.25、0.18、0.14、0.1,0.03,ky、kz分别为y和z方向的刚度系数.本文采用动力学模型修正的方法,主要步骤如下.

1）建立机床的动力学模型,确定边界条件和结合面初值,进行模态分析.

2）结果文件提取（固有频率）.

3）依次改变弹簧阻尼单元各方向的刚度.

4）重新进行求解计算.

5）应用式（11）进行计算.

6）重复步骤2）～5）,直至式（11）的计算结果满足阈值.

设阈值为0.001,经多次迭代,当ky＝3.5×105N／m3、kz＝4.6×105N／m3时,各阶模态的仿真频率和对应的实验频率误差控制在3%以下,如表3所示.此时查表获得阻尼系数分别为cy＝1.2×105N·s／m3,cz＝6.1×105N·s／m3.

从参数优化前、后的结果来看,理论分析给出的结合面参数与模态实验最终优化得到的参数存在差别,主要原因如下.1）误差控制在3%以下,若降低误差要求,则两者差别会减小.2）相比较而言,y方向的刚度和阻尼值差别较大,z方向差别较小,是因为第2阶模态“立柱整体左右摆动”实验和仿真频率值差别较大,而该阶模态主要决定于y方向的刚度和阻尼系数.为了降低实验和仿真的差值,将y方向的系数作了较大调整.最后,理论计算和实验优化后的值基本都在同一个数量级上,在工程上是可以接受的.

表3 机床整机模态仿真和实验结果比较Tab.3 Comparison of machine tool simulation and experimental results

3 基于试验设计的切削稳定性响应面构建

以修正后的有限元模型为基础进行计算,在主轴箱和立柱各自的行程中取3个特殊位置：主轴箱位于立柱的顶部、中部、底部；因为该加工中心的结构左、右对称,立柱位于左部和右部的对应位置时结构性能大体一致,因此取立柱在右边的位置进行分析.令立柱分别位于原点（整个行程的中心位置）、中部（原点与右端部的中间位置）、右端部.立柱和主轴箱的位置组合一共有3×3＝9种组合,以此为样本点进行试验设计.

3.1 切削稳定性响应面的构造

响应面法是一种采用试验设计理论对指定的设计点集合进行试验,得到目标函数和约束函数的响应面模型,来预测非试验点的响应值的方法.一般响应面模型采用二阶模型,对于n个变量的情况,二次多项式响应面模型为

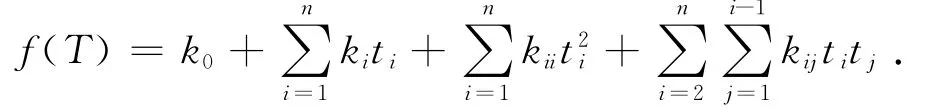
式中：T＝（t1,t2,…,tn）,ti（i＝1,2,…,n）为设计变量,k0、ki、kii、kij为未知系数,系数个数L＝（n＋1）（n＋2）／2.

设由试验设计确定的样本点组成的设计变量矩阵为T,系数组成的矩阵为K,通过有限元分析和式（4）计算得到结果向量F.令式（4）计算的结果和响应面的逼近值之间的误差组成的向量为ε,则有

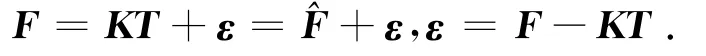
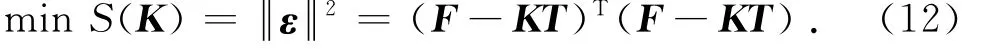
根据式（12）取极值的必要条件可以进一步求得

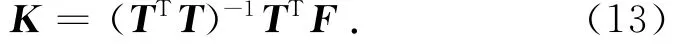
将T和F代入式（13）,即可求得系数矩阵K.

响应面模型对样本数据拟合度可用均方根误差相对值（RMSE）和决定系数R2两个标准检验,表达式分别为

3.2 切削稳定性的正交实验

本文的实验设计比较简单,共2因子3水平,因此采用全因子实验,即L9（23）共9组实验数据.以立柱在水平位置的中心点为原点,以立柱位置与原点的距离和水平行程的比值为变量,定义立柱的位置变量的集合如下：

X＝（立柱位置与原点距离／行程）＝｛原点,中部,端部｝＝｛0,0.5,1｝.

同理定义主轴箱在立柱上的中点位置为原点,位置变量的集合为

Y＝（主轴箱位置与原点距离／行程）＝｛底部,中部,顶部｝＝｛0,0.5,1｝.

9组实验的集合为

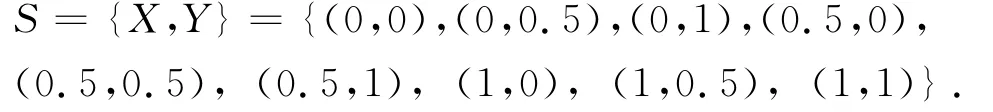
如（X,Y）＝（0.5,1）表示立柱在水平位置的中点,主轴箱在顶部.

采用子结构有限元计算方法［8］,将立柱和主轴箱分别设为子结构,根据计算获得立柱位于原点,主轴箱位于顶部和底部时,机床的动力学性能如表4所示.同理,获得立柱分别在左端部和右端中部、主轴箱在不同位置时机床的动力学性能,如表5、6所示.

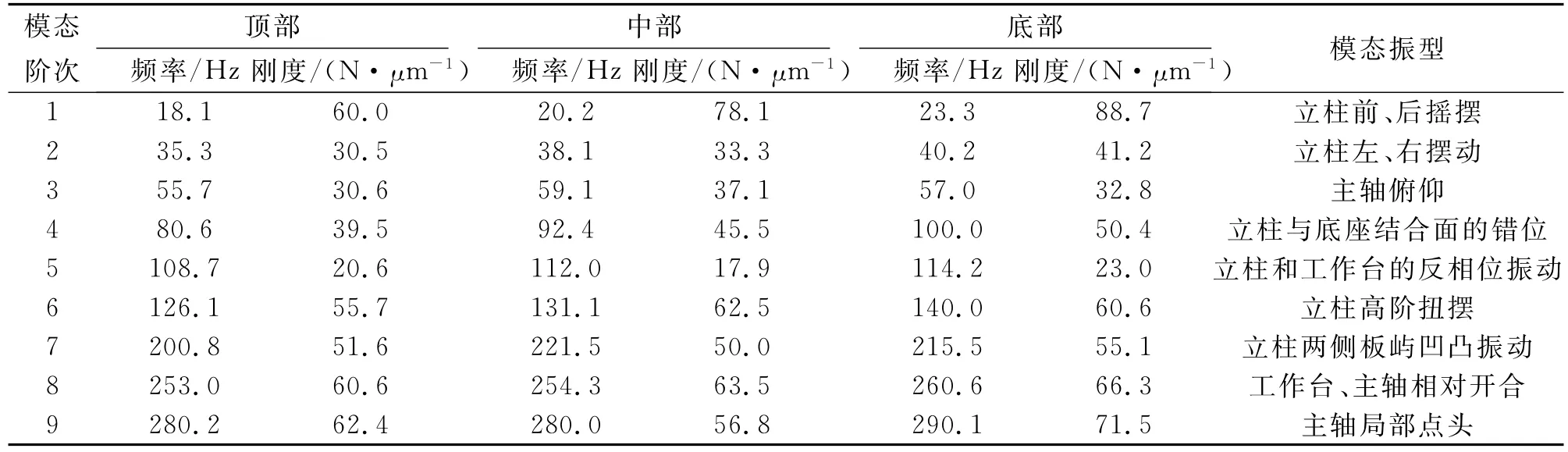
表4 立柱位于原点,主轴箱在不同位置时机床的动力学性能Tab.4 Dynamics of column in origin positions and spindle box in different position

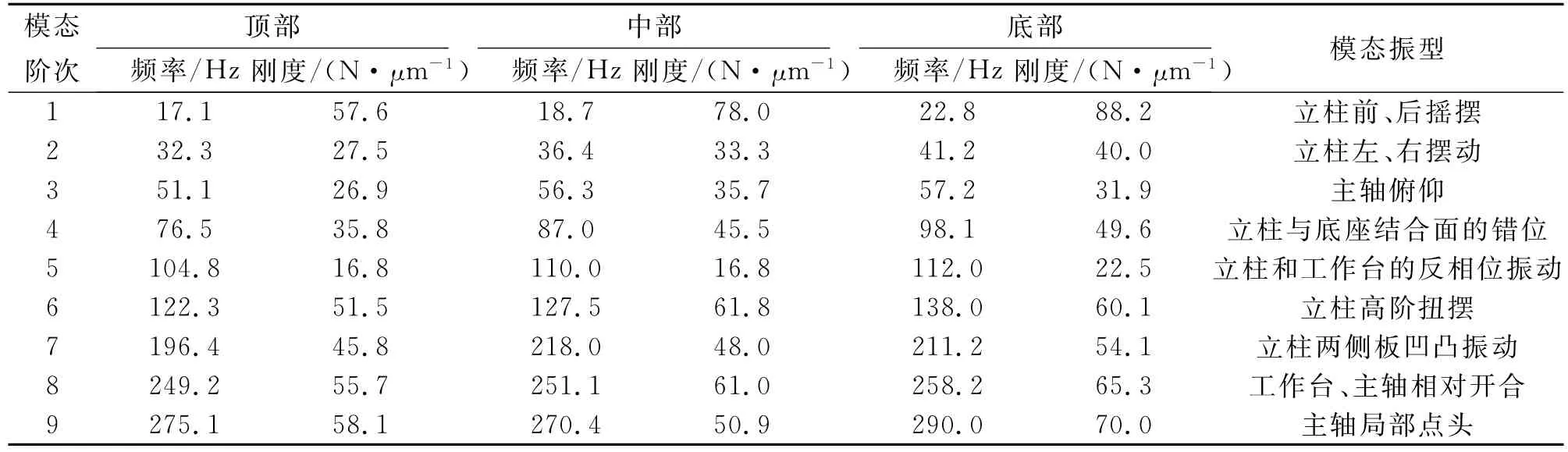
表5 立柱位于左端部,主轴箱在不同位置时机床的动力学性能Tab.5 Dynamics of column in left end point and spindle box in different position

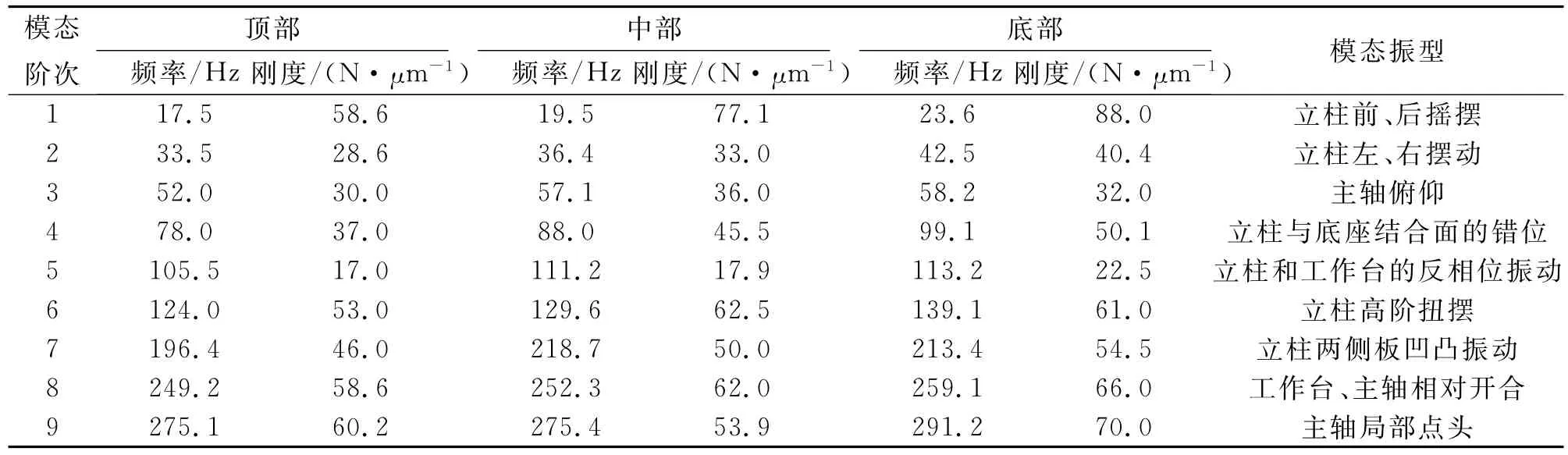
表6 立柱位于右端中部,主轴箱在不同位置时机床的动力学性能Tab.6 Dynamics of column in right center point and spindle box in different position

由表4～6可以看出,主轴箱在立柱上的位置对机床的动力学性能的影响较大.当立柱位置固定时,主轴箱在顶部、中部、底部位置的固有频率依次提高,动刚度依次增大,但变化的幅度逐步减小；当主轴箱位置固定时,立柱的不同位置对整机的动力学性能整体来说较小,相对来说立柱越靠近端部,对整体的性能影响越大；模态的阶次越高,受到的影响越大；立柱、主轴箱的位置变化对动刚度的影响比对固有频率的影响大.设本文所使用的刀具参数和切削力系数如下：切削方式为顺铣、干切削,刀具直径D为20 mm,齿数N＝3,螺旋角β＝45°,每齿进给量Fz＝0.1 mm,径向切深ae＝8 mm,铣削力系数Kt＝540 N／mm2,Kr＝0.33.

将切削参数代入公式C＝－1／（NKrKt）,可得C＝－1.87×10－3（m2／N）.

一般来说,机床的最小临界切削深度主要取决于刚度最小的某阶模态［2］,在本文中即第5阶模态,对应振型是立柱和工作台的反相位振动.根据该阶模态的参数计算最小临界切削深度,将各项参数代入式（4）,获得各个不同位置的计算结果如表7所示.

表7 机床在不同位置时的最小临界切削深度Tab.7 Minimum critical cutting depth in different position mm

3.3 切深稳定性响应面模型质量的检验

根据表7的数据,整理为变量矩阵T和结果矩阵F,即

代入式（13）,可得系数矩阵：

K＝

［0.118 2,－0.318 5,－0.771 0,0.009,－0.216 6］,常数项为1.39.

响应面方程为

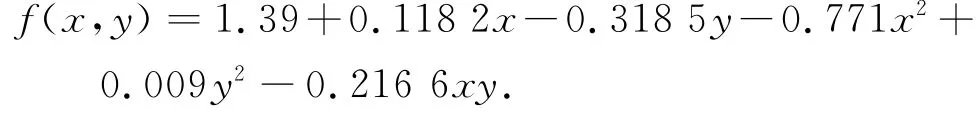
根据响应面的质量检验公式,分别代入式（14）计算可得

响应面的误差及其与原模型的相似度是满足要求的.根据该模型,求得稳定切削极限深度与立柱和主轴箱位置的关系,如图8、9所示.图中,s为立柱的位置与行程之比.

从图8、9可以看出：立柱的不同位置对于机床的最小临界切削深度有影响,而且主轴箱的位置越高或者立柱的位置越靠近端部时影响越明显,前者的影响比后者大；当主轴箱位于底部和中部时,立柱位置的影响不明显；当主轴箱位于顶部并且立柱位于端部时,机床的最小临界切削深度比其他位置有大幅度降低.仅考虑主轴箱在不同位置时的切削稳定性是不完整的,忽略立柱位置影响获得的最小临界切削深度是有误差的.根据该切削深度来选择切削参数极有可能导致切削不稳定的产生,必须全面考虑主轴箱和立柱在不同位置组合情况下的切削稳定性以获得最佳切削参数.

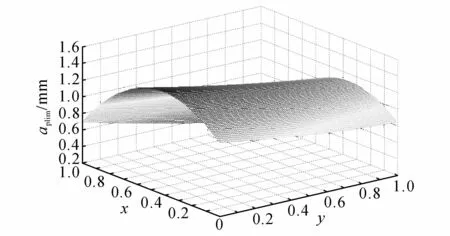
图8 最小临界切削深度与立柱和主轴箱位置的关系Fig.8 Relation between minimum critical cutting depth and column and spindle box position

4 结 论

（1）本文提出广义空间切削稳定性的概念,利用响应面模型模拟出机床的稳定性最小临界切削深度在广义加工空间中的变化规律,涵盖了立柱的位置和主轴箱的位置在加工空间的随机组合,克服了传统的忽略机床加工位姿对动力学特性影响的不足.

（2）以模拟导轨-滑块结合部的弹簧阻尼单元刚度系数为对象,通过比较模态实验结果和有限元模型仿真结果,以相同振型的频率误差最小作为目标函数,调整结合面的相关参数,从而得到准确的有限元模型,为稳定性的计算提供了保证.

（3）对一台卧式加工中心进行广义切削稳定性分析,获得了机床在整个加工空间内最小临界切削深度的变化规律.切削稳定性深度函数的三维图形显示：在主轴箱位置固定的情况下,立柱越靠近行程的端部,机床的最小临界稳定性切削深度越低,而且主轴箱的位置越高该变化趋势越明显；当主轴箱位于底部和中部时,立柱位置的变化对切深的影响不大；当主轴箱位于顶部并且立柱位于端部时,机床的最小临界切削深度比其他位置有大幅度降低.

［1］ALTINTAS Y.Manufacturing Automation［M］.Cambridge：Cambridge University Press,2000.

［2］刘强,李忠群.数控铣削加工过程仿真与优化-建模、算法与工程应用［M］.北京：航空工业出版社,2011.

［3］HUNG Jui-pin,LAI Yuan-lung,LIN Ching-yuan.Modeling the machining stability of a vertical milling machine under the influence of the preloaded linear guide［J］.International Journal of Machine Tools and Manufacture,2011,51（9）：731- 739.

［4］ZULAIKA JJ,CAMPA F J,LOPEZ L N.An integrated process machine approach for designing productive and lightweight milling machines［J］.International Journal of Machine Tools and Manufacture,2011,51（7）：591- 604.

［5］GRAHAM E,MEHRPOUYA M,PARK S S.Robust prediction of chatter stability in milling based on the analytical chatter stability［J］.Journal of Manufacturing Processes,2013,15（4）：508- 517.

［6］刘海涛,赵万华.基于广义加工空间概念的机床动态特性分析［J］.机械工程学报,2010,46（21）：54- 60.

LIU Hai-tao,ZHAO Wan-hua.Dynamic characteristic analysis for machine tools based on concept of generalized manufacturing space［J］.Journal of Mechanical Engineering,2010,46（21）：54- 60.

［7］MOHIT L,ALTINTAS Y,SRIKANTH A.Rapid evaluation and optimization of machine tools with position dependent stability［J］.International Journal of Machine Tools and Manufacture,2013,68（3）：81- 90.

［8］SCHMITZ T L,DAVIES M A,KENNEDY M D.Tool point frequency response prediction for high-speed machining by RCSA［J］.Journal of Manufacturing Science and Engineering,2001,123（4）：700- 707.

［9］关振群,顾元宪,张洪武,等.三维CAD／CAE一体化的参数化动态有限元建模［J］.计算机集成制造系统, 2003,9（12）：2112- 2119.

GUAN Zhen-qun,GU Yuan-xian,ZHANG Hong-wu,et al.A parameterized method for 3D finite element modeling based on CAD／CAE［J］.Integration Computer Integrated Manufacturing Systems,2003,9（12）：2112- 2119.

［10］廖伯瑜,周新民,尹志宏.现代机械动力学及其工程应用［M］.北京：机械工业出版社,2004.

［11］蒋书运,祝书龙.带滚珠丝杠副的直线导轨结合部动态刚度特性［J］.机械工程学报,2010,46（1）：92- 99.

JIANG Shu-yun,ZHU Shu-long.Dynamic characteristic parameters of linear guideway joint with ball screw［J］.Journal of Mechanical Engineering,2010,46（1）：92- 99.

Research on cutting stability of generalized manufacturing space based on response surface mode

HUANG Hua1,2,ZHANG Shu-you1,LIU Xiao-jian1,HE Zai-xing1
（1.State Key Laboratory of Fluid Power Transmission and Control,Zhejiang University,Hangzhou 310027,China；2.School of Mechanical and Electrical Engineering,Lanzhou University of Science and Technology,Lanzhou 730050,China）

A method of combining the response surface mode（RSM）and experimental design was presented based on the combination of different positions in the moving trajectory of the machine tool spindle box and the column in order to analyze the cutting stability in the whole processing spatial distribution.A combination at key position was selected as samples,and the dynamics property of the samples was calculated via ANSYS.The limit critical cutting depth of each sample was calculated,and the quadratic polynomial RSM reflecting the relation between position and stability of limit critical cutting depth was established.The limit critical cutting depth in the entire space approximation was calculated,and the quality of RSM was further evaluated.The great influence of position changes of moving parts on the stability of cutting was shown with a high speed horizontal machining center（MC）as an example,providing some theoretical support for optimization of machining process and structure design.

cutting stability；limit critical cutting depth；generalized workspace；response surface model（RSM）

张树有,男,教授,博导.E-mail：zsy＠zju.edu.cn

TG 502；TP 391

A

1008- 973X（2015）07- 1215- 09

10.3785／j.issn.1008-973X.2015.07.003

2014- 10- 16. 浙江大学学报(工学版)网址：www.journals.zju.edu.cn／eng

国家自然科学基金资助项目（51275458）；浙江省博士后科研资助项目（BSH1401013）；国家科技重大专项课资助项目（2015ZX04014021）.

黄华（1978－）,男,博士后,副教授,从事产品数字化设计、复杂装备设计与仿真分析的研究.ORCID：0000-0002-4945-5888.

E-mail：huanghua＠zju.edu.cn