基于子模式双向二维线性判别分析的人脸识别

董晓庆，陈洪财

（韩山师范学院物理与电子工程学院，广东潮州521041）

基于子模式双向二维线性判别分析的人脸识别

董晓庆∗，陈洪财

（韩山师范学院物理与电子工程学院，广东潮州521041）

针对表情和光照变化等对人脸识别影响的问题，提出一种基于子模式双向二维线性判别分析（Sub-pattern two-directional two-dimensional linear discriminant analysis，Sp-（2D）2LDA）的人脸识别方法.该方法首先对原图像进行分块处理，并保持子块间的空间关系，然后对各个子训练样本集从行方向和列方向同时利用2DLDA进行特征抽取，最后把各个子特征矩阵拼接成一对应原始图像的特征矩阵，并采用最近邻分类器进行分类识别.在ORL及Yale人脸库上的试验结果表明，Sp-（2D）2LDA有效降低了鉴别特征的维数，减少了表情和光照变化的影响，获得了较好的识别性能.

人脸识别；特征抽取；双向二维线性判别分析；子模式双向二维线性判别分析

1　引 言

人脸识别［1-2］是计算机视觉和模式识别的一个研究热点.由于面部表情、光照变化、姿态等因素的影响，人脸识别仍然是非常具有挑战性的工作［3］.特征提取是人脸识别的关键环节，其中最具代表性的方法之一就是线性判别分析（linear discriminant analysis，LDA）［4］，作为特征提取和数据描述的有力工具，在人脸识别领域得到了广泛的应用［5-6］.但是，LDA具有两个明显的缺点:缺点1，需要将二维图像矩阵转化为一维图像向量，造成图像向量的维数一般较高，在大尺寸和小样本的情况下，很难精确地对协方差矩阵进行求解，并且得到的类内离散度通常都是奇异的［7-8］；缺点2，LDA只利用了图像的全局信息，对人脸表情和光照条件的变化敏感.

针对缺点1，Li和Yuan提出了二维线性判别分析（2DLDA）方法［9］，该方法不必将人脸图像矩阵转化为人脸图像向量，而是直接利用人脸图像矩阵计算类内和类间离散度矩阵.文献［9］表明，2DLDA估计得到的离散度矩阵比LDA方法精确.鉴于这些优点，近几年来2DLDA方法被广泛应用于人脸识别领域［10-11］.但是2DLDA提取的特征向量维数一般较高，它需要比LDA更多的系数来表示人脸图像，这增加了识别时间.为了解决这一问题，文献［12］又提出了双向二维线性判别分析（（2D）2LDA）.（2D）2LDA同时从行和列两个方向对原始图像进行特征提取，即进行了双向压缩，从而大大降低了特征向量的维数.

针对缺点2，文献［13-14］提出了分块LDA（MLDA）的方法，该方法对图像矩阵进行分块处理，有效地降低了光照、表情等变化因素的影响，并充分利用人脸的局部特征，使得识别算法更俱鲁棒性.为了进一步降低的特征向量的维数，王磊等人［15］提出了一种基于双向模块2DLDA（M（2D）2LDA）的方法，该方法在分块图像的基础上，利用双向2DLDA进行特征抽取，即有效地降低光照对人脸的影响，利用了图像的局部特征，又降低了特征维数.但是上述的模块化算法把所有的子块作为一个新的训练样本集进行特征抽取，没有合理的利用子块间的空间关系，这限制了识别率的进一步提高，文献［16］提出了子模式的概念，保留了子块之间的空间关系，文献［17］将子模式的思想应用于双向二维主成分分析（（2D）2PCA），提出了子模式双向二维PCA方法（Sp-（2D）2PCA），减少了光照、表情的影响，进一步提高了识别性能.

本文借鉴文献［16］的思想，结合子模式和（2D）2LDA的优点，提出了一种子模式双向2DLDA（Sp-（2D）2LDA）的人脸识别方法，该方法首先将原图像矩阵等分为多个子块，将相同位置的子块分别组成各个子训练集，然后对每个子训练集使用（2D）2LDA进行提取特征，最后将这些提取的子特征拼接成一全局特征.与文献［15］将所有的子图像组成一个新的训练样本集不同，本文算法将相同位置的子图像组成子训练样本集进行特征抽取，然后再将特征抽取所得到的局部子特征按照空间位置重新组合成全局特征，有效地利用了子图像的空间位置关系，进一步提高了识别率.与文献［17］基于双向二维PCA不同，本文算法基于双向二维LDA，其有效地利用了类间的鉴别信息，能提取到更有利于识别的特征，进一步提高了识别性能.ORL和Yale人脸库上的试验结果表明，与2DLDA、（2D）2LDA、模块2DLDA（M2DLDA）和M（2D）2LDA等方法比较，本文方法具有更好的识别性能.

2　2DLDA及双向2DLDA

2.12DLDA

2DLDA的目标就是寻找一最优的投影向量X，使得式（3）定义的fisher准则最大:

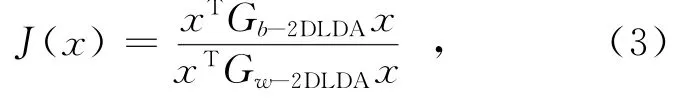
式中T表示转置.最大化式（3）即是同时保证类内距离最小化及类间距离最大化.由于类内离散度矩阵Gw-2DLDA一般情况下都是非奇异的［16］，求解最优投影向量可转化为计算Gb-2DLDAG-1w-2DLDA的特征值及特征向量，最大特征值所对应的特征向量就是所求的最优投影向量.但是，在样本类别数较多的情况下，单一的最优投影向量是不够的.因此，一般情况下需要一组满足标准正交条件且极大化fisher准则（3）的最优投影向量组x1，x2，…xd.文献［19］指出，最优投影向量组可取Gb-2DLDAG-1w-2DLDA的前d个最大特征值所对应的特征向量x1，x2，…xd，那么大小为n×d的投影矩阵X=［x1，x2，…xd］就是所求的最优投影矩阵.

2.2扩展2DLDA

（2D）2LDA认为2DLDA实质上是对图像行方向的运算，其消除了图像列之间的相关性，并把水平方向上的判别信息压缩在极少的列上.然而，它忽视了图像行之间的相关性和垂直方向上的判别信息压缩［12，20］.为了消除图像行之间的相关性和压缩垂直方向的判别信息，文献［12］提出了扩展的2DLDA（E2DLDA）.式（1）、（2）的类间离散度矩阵及类内离散度矩阵［17］可重新定义如下:

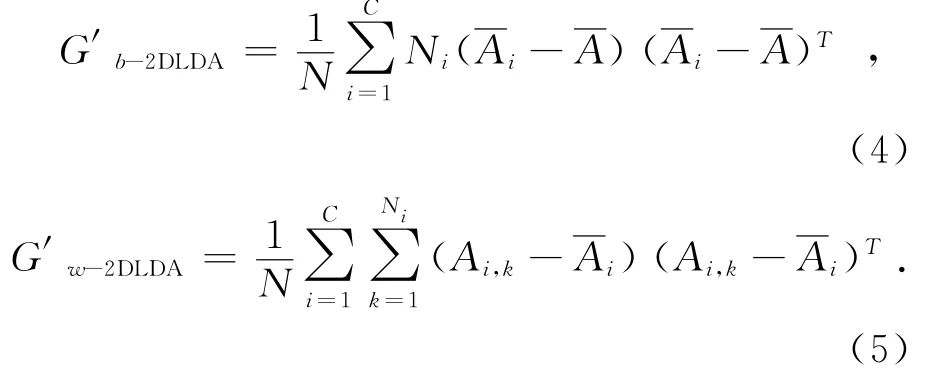
相应地，fisher准则定义如下:

E2DLDA的目标是寻找一组满足标准正交条件且极大化fisher准则函数式（6）的最优投影向量组z1，z2，…zd.与2DLDA类同，最优投影向量组z1，z2，…zd可取G′b-2DLDAG′-1w-2DLDA的前d个特征向量.令Z=［z1，z2，…zd］，那么投影矩阵Z就是列方向E2DLDA的最优投影矩阵.

2.3双向2DLDA

假设通过行方向2DLDA和列方向E2DLDA运算后，分别得到了行方向投影矩阵X（X∈Rn×d（d≤n））和列方向投影矩阵Z（Z∈Rm×g（g≤m）），（2D）2LDA把m×n图像A同时向X和Z投影，产生一个g×d矩阵Y为

Y即为（2D）2LDA在图像A上提取的特征矩阵，把每一个m×n训练样本图像Ai，k投影到X及Z上，得到g×d的训练样本的特征矩阵Yi，k，因为g值一般小于m，d值一般小于n，所以相比行方向2DLDA及列方向E2DLDA所提取的特征矩阵维数（m×d或g×n），（2D）2LDA有效地降低了特征矩阵的维数.

3　本文算法SP-（2D）2LDA

图1　Yale库中部分人脸，（a）、（c）标准人脸；（b）、（d）表情、光照变化人脸；（e）～（h）为（a）～（d）的2×2分块人脸Fig.1　Samples from the Yale database.（a）and（c）are normal images.（b）and（d）are variations in facial expression and illumination.（e）～（h）are the sub-images by dividing the（a）～（d）into four blocks，respectively

如图1所示，图像（a）、（c）为标准的人脸，没有受到光照不均、表情变化或姿态等的影响，（b）、（d）为表情、光照变化的人脸图像.对于上述的非模块化算法而言，检测标准人脸图像的识别率已经非常高，但当人脸受到表情、光照变化等的影响时，识别率就会下降，因为其提取的是全局的特征，而这些特征跟标准图像的特征是不一样的，这导致了识别率的下降.如果对这些人脸图像进行模块化处理，如图像（e）～（h）所示.将人脸图像（e）、（f）进行比较，人脸图像下半部分子图像变化比较大，而上半部分相对变化小很多，即把受影响的部分局限在部分子块里，而其他子块并不会受到影响.那么下半部分两个子图像的识别难度将比较大，而上部的子图像识别会比较容易，因此，如果我们采用子模式的分块处理方法，将各个人脸图像相同位置的子图像组成子训练集计算其子投影矩阵，而不是将所有的子图像组合成一个训练集，这将有助于提高识别率.同理，如图像（f）所示，只有左半部分的子块受到光照的影响，而右边的子块跟标准图像几乎一样，采用子模式的方式进行特征提取，将有助于识别率的进一步提高.所以，本文提出了一种基于子模式双向2DLDA的特征提取方法，该方法实现步骤如下:

3.1构造子模式训练集

SP-（2D）2LDA首先将原始图像矩阵A分成N=p×q个子图像，p、q分别表示行、列方向的子块数目.该分块矩阵如下所示:

式中:Ai，k（k=1，2....Ni）表示i类中的第k个样本图像，（Bi，k）xy（x=1，2…，p；j=1，2…，q）表示子图像，各个子图像的行数和列数分别为m1= m/p和n1=n/q.设共有N幅训练样本图像，将所有原训练样本图像中对应位置的子图像（Bi，k）xy组成相应的子模式训练集Txy，每个子训练集的样本总数都为N.

3.2求取最优投影矩阵

由步骤（1）中的子训练集Txy可知，行方向类间离散度矩阵Gb-2DLDA及类内离散度矩阵Gw-2DLDA分别为:

同理可以构造子训练集Txy的列方向类间离散矩阵（G′b-2DLDA）xy及类内离散度矩阵（G′w-2DLDA）xy，分别为:

3.3特征提取

同理，测试样本At的特征矩阵为:

最后，计算测试样本与训练样本特征矩阵之间的欧氏距离，利用最近邻分类器进行分类.

4　实验结果及分析

实验中采用标准的人脸数据库ORL及Yale，将本文算法SP-（2D）2LDA与2DLDA、（2D）2LDA、M2DLDA、M（2D）2LDA进行比较.实验平台为奔腾双核CPU E5800 3.2G，2G RAM，Windows XP操作系统，利用MATLAB2010进行仿真实验.

4.1ORL人脸库上的实验

剑桥大学ORL人脸图像库是人脸识别领域常用的图像库，该库由40个人每人10幅图像共400幅灰度图像组成，图像灰度级为256，分辨率为112×92，库中图像包括了光照、表情、姿势、年龄的变化等.

本实验测试相关算法在不同训练样本数下的识别率，训练样本数分别为S=2～8，剩下的10-S个样本作为测试样本.为了消除样本选择的随机性，每种样本数下的实验均重复独立进行20次，最后取平均识别率，实验中特征向量数为10，分块算法采用2×2的分块情形.图2为ORL库中某一人的5幅图像.

图2　ORL库中某一人的5幅图像Fig.2　Five images of one person from the ORL face database

由图3可以看出，随着训练样本数目的增加，识别率的总体趋势是向上的.当训练样本数小于5时，识别率增长得快一些，训练样本数大于5时识别率增长相对平缓.从M2DLDA与2DLDA，SP-（2D）2LDA、M（2D）2LDA与（2D）2LDA这两组数据比较来看，基于模块化处理的算法识别率要比非模块化算法识别率高一些，因为分块处理有效提取到一些局部特征，有利于减少表情、光照变化的影响.而本文提出的算法SP-（2D）2LDA在各种样本数目下的识别率都是最高的，因为SP-（2D）2LDA算法不但同时利用了行列方向的特征，而且在分块时保持了子块间的空间关系，因此取得了更好的识别性能.

图3　各种算法在不同训练样本数下的识别率Fig.3　Recognition rates of the related methods with varying number of sample size

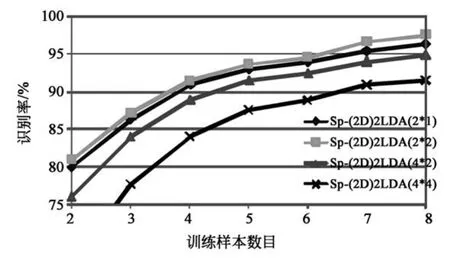
图4　本文算法不同分块在各种训练样本数下的识别率Fig.4　Recognition rates of the proposed method with varying number of sample size

图4为本文算法SP-（2D）2LDA不同分块情况下的识别率，分块取N=2（2×1）、4（2×2）、8（4× 2）、16（4×4）.如图4所示，随着样本数量的增加，识别率的总体趋势向上.SP-（2D）2LDA在分块数为2、4、8时识别效果比较好，其中分块数4取得了最优的识别性能.而分块数为16时，识别率下降比较多，识别效果反而不如非模块处理的算法，这说明了分块数并非越多越好，因为太多的分块有可能导致提取不到人脸图像的整体信息.

4.2Yale人脸库上的实验

Yale人脸数据库由15人、每人11幅共165幅人脸图像组成.图像包括了各种表情变化，如悲伤、高兴、惊喜等.还有光照变化，如左侧光照及右侧光照.为了减少背景成分对识别性能的影响，对每幅图像以人脸为中心提取尺寸为100× 100的子图像，如图5所示.

图5　Yale数据库中的某一人的5幅图像Fig.5　Five images of one person from theYale face database

本实验测试相关算法在不同特征向量数下的识别率，特征向量数为1～20.训练样本数为6，测试样本数为5，分块算法采用2×2的分块情形.跟ORL人脸库实验类似，为了消除单次样本选择的随机性，每次实验均重复独立进行20次，最后取平均识别率.

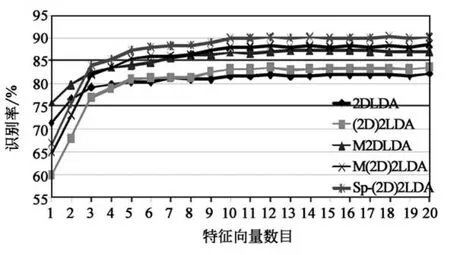
图6　各种算法在不同特征向量数下的平均识别率Fig.6　Average recognition rates of the related methods with varying number of eigenvectors

图6给出了识别率与鉴别特征向量维数的关系.如图所示，随着特征向量数目的逐渐增加，各种方法的识别率均在逐渐增加，当特征向量数≥5时识别率趋于稳定；从M2DLDA和2DLDA，M（2D）2LDA、Sp-（2D）2LDA和（2D）2LDA二组数据的比较结果可以看出，将原图像分块有效地捕捉了局部信息，提高了识别率.尽管在特征向量数低于3时，子模式双向2DLDA的识别率不如M2DLDA和2DLDA，但随着特征向量数的提高，本文算法取得了最高的识别率，因为本文算法同时利用了行列方向的鉴别信息，而且利用子模式的分块方法，有效提取到一些局部特征，并减少光照及表情的影响，所以本文算法具有更好的识别性能及鲁棒性.

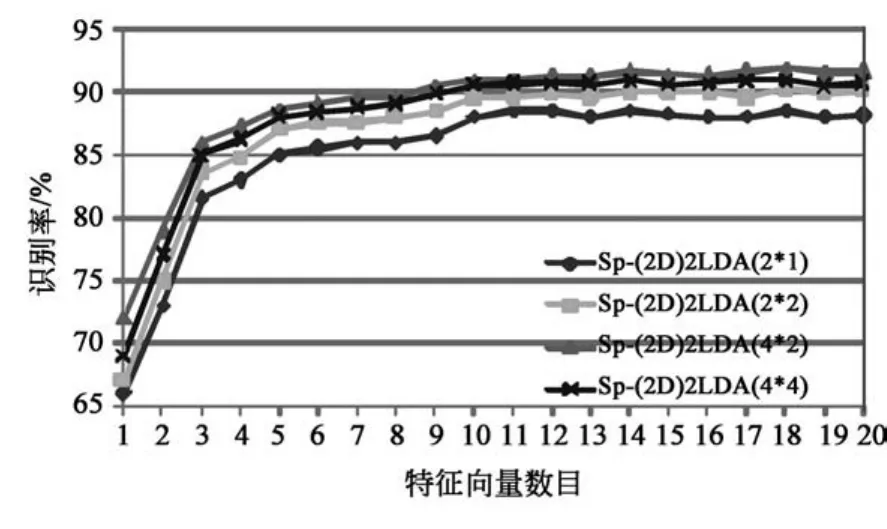
图7　Sp-（2D）2LDA不同分块情况在各种特征向量数下的平均识别率Fig.7　Average recognition rates of the proposed method with varying number of eigenvectors

图7为本文算法SP-（2D）2LDA取不同分块数时的识别率，与ORL人脸库上的实验一样，分块数也取N=2（2×1）、4（2×2）、8（4×2）、16（4×4）.如图所示，随着特征向量数的增加，各种不同分块的识别率也跟着增加，当特征向量数目大于3时，识别率趋于稳定.比较2、4、8这3种分块的识别结果可知，当分块数增加时，识别率也随着增加，因为模块化处理有利于减少光照、表情变化等的影响，分块数增加时，能使受影响的范围缩小，从而提高了识别率.但当分块数为16时，识别率反而比分块数为8时有所下降，这同样说明分块数不是越多越好，因为太多的分块有可能破坏了人脸图像的全局信息.

从ORL及Yale人脸库的实验结果来看，本文算法Sp-（2D）2LDA在ORL人脸库取得最优性能的分块数为N=4，而在Yale人脸库上取得最优性能的分块数为N=8，即本文算法在不同人脸库上取得最优性能的分块数是不同的，分块数的选择需根据具体人脸库的特征进行确定.

5　结 论

本文提出了一种Sp-（2D）2PCA的特征提取方法，并应用于人脸识别.该方法通过将原始图像进行分块，并保留子块之间的空间关系，减少了人脸表情和光照变化的影响，有效地捕捉到人脸的局部信息.利用（2D）2LDA进行特征抽取，在行列方向都进行特征压缩，有效地降低了特征向量的维数.实验结果表明，本文方法通过结合子模式分块处理方法和双向2DLDA的优点，获得了更高的识别性能.

［1］ 李鹏飞，许金凯，韩文波，等.基于S3C2440的人脸识别平台的设计［J］.液晶与显示，2014，29（3）:417-421.

Li P F，Xu J K，Han W B，et al.Design of face identification platform based on S3C2440［J］.Chinese Journal of Liquid Crystals and Displays，2014，29（3）:417-421.

［2］ 李定珍，郭建昌.B2DPCA和ELM人脸识别算法研究［J］.液晶与显示，2013，28（3）:440-445.

Li D Z，Guo J C.Face recognition algorithm based on B2DPCA and ELM［J］.Chinese Journal of Liquid Crystals and Displays，2013，28（3）:440-445.

［3］ Adini Y，Moses Y，Ullman S.Face recognition:The problem of compensating for changes in illumination direction［J］.Pattern Analysis and Machine Intelligence，IEEE Transactions on，1997，19（7）:721-732.

［4］ Belhumeur P N，Hespanha J P，Kriegman D J.Eigenfaces vs.Fisherfaces:recognition using class specific linear projection［J］.IEEE Trans.Pattern Anal.Mach.Intell.1997，19（7）:711-720.

［5］ 周大可，杨新，彭宁嵩.改进的线性判别分析算法及其在人脸识别中的应用［J］.上海交通大学学报，2005，39（4）:527-530.

Zhou D K，Yang X，Peng N S.A modified linear discriminant analysis and its application to face recognition［J］. Journal of Shanghai Jiaotong University，2005，39（4）:527-530.（in Chinese）

［6］ Zhuang Z M，Zhang A N，Li F L.Based on an optimized LDA algorithm for face recognition［J］.Journal of Electronics&Information Technology，2007，29（9）:2047-2049.

［7］ Yu H，Yang J.A direct LDS algorithm for high-dimensional data with application to face recognition［J］.Pattern Recognition，2001，34（10）:2067-2070.

［8］ Yang J，Zhang D，Frangi A F，et al.Two-dimensional PCA:A new approach to apperarance-based face representation and recognition［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2004，26（1）:131-137.

［9］ Ming L，Yuan B.2D-LDA:a statistical linear discriminant analysis for image matrix［J］.Pattern Recognition Letter，2005，26（5）:527-532.

［10］ Yang J，Zhang D，Xu Y，et al.Two-dimensional discriminant transform for face recognition［J］.Pattern Recognition，2005，38（7）:1125-1129.

［11］ Yang W，Yan X，Zhang L，et al.Feature extraction based on fazzy ZDLDA［J］.Neurocomputing，2010，73（1012）:1556-1561.

［12］ Noushath S，Kumar G H，Shivakumara P.（2D）2LDA:An efficient approach for face recognition［J］.Pattern Recognition，2006，39（7）:1396-1400.

［13］ 王文豪，严云洋.基于图像分块的LDA人脸识别［J］.计算机工程与设计，2007，28（12）:2889-2891.

Wang W H，Yan Y Y.LDA for face recognition based on images egmentation［J］.Computer Engineering and Design，2007，28（12）:2889-2891.（in Chinese）

［14］ 延伟东，彭国华.基于分块FLD的图像特征提取方法［J］.科学技术与工程，2006，6（19）:3107-3110.

Yan W D，Peng G H.Image feature extracting approach based on blocked FLD［J］.Science Technology and Engineering，2006，6（19）:3107-3110.（in Chinese）

［15］ 王磊，武敬飞，贾莉.一种基于双向模块2DLDA的人脸识别方法［J］.电子测量与仪器学报，2013，27（8）:760-765.

Wang L，Wu J F，Jia L.Face recognition method based on bidirectional and modular 2DLDA［J］.Journal of Electronic Measurement and Instrument，2013，27（8）:760-765.（in Chinese）

［16］ Chen S C，Zhu Y L.Subpattern-based principal component analysis［J］.Pattern Recognition，2004，37（1）: 1081-1083.

［17］ 张先武，郭雷.基于子模式双向二维主成分分析的人脸识别［J］.光电子·激光，2009，20（11）:1498-1502.

Zhang X W，Guo L.Face recognition based on sub-pattern two-directional 2DPCA［J］.Journal of Optoelectronics·Laser，2009，20（11）:1498-1502.（in Chinese）

［18］ Han K，Zhu X.Research on two-dimensional lda for face recognition［J］.Journal of Electronics（China），2006，23（6）:943-947.

［19］ Li M，Yuan B Z.2D-LDA:A statistical linear discriminant analysis for image matrix［J］.Pattern Recognition Letters，2005，26（5）:527-532.

［20］ 杜海顺，柴秀丽，汪凤泉，等.一种基于双向2DLDA特征融合的人脸识别方法［J］.仪器仪表学报，2009，30（9）:1880-1885.

Du H S，Chai X L，Wang F Q，et al.Face recognition using a fusion method based on bidirectional 2DLDA［J］. Chinese Journal of Scientific Instrument，2009，30（9）:1880-1885.（in Chinese）

Face recognition based on sub-pattern
two-directional two-dimensional linear discriminant analysis

DONG Xiao-qing∗，CHEN Hong-cai

（School of Physics and Electronic Engineering，Hanshan Normal University，Chaozhu 521041，China）

To reduce the impacts of the variations of expression and illumination，a novel face recognition method based on sub-pattern two-directional two-dimensional linear discriminant analysis（Sp-（2D）2LDA）is presented in this paper.Firstly，Sp-（2D）2LDA divides the original images into smaller sub-images and keeps the spatial relationship between the sub-images.Secondly，it simultaneously applies 2DLDA to the subsets of the training samples in the row and column directions to extract local sub-features.Finally，the sub-features are synthesized into global features and nearest neighbor classifier is used for classification.The experimental results on Yale and ORL face databases show that the proposed Sp-（2D）2LDA method effectively reduce not only the dimension of the eigenvectors，but also the influence of variations in illumination and facial expression.Thus，the proposed method has better classification performances than the other related methods.

face recognition；feature extraction；two-directional two-dimensional linear discriminant analysis；sub-pattern two-directional two-dimensional linear discriminant analysis

TP391

A doi:10.3788/YJYXS20153006.1016

1007-2780（2015）06-1016-08

董晓庆（1982-），男，广东潮州人，讲师，硕士，主要研究方向为机器视觉、模式识别、自动控制.E-mail:dxqzq110@163.com；

陈洪财（1967-），男，山东菏泽人，副教授，主要研究方向为智能控制及嵌入式系统.E-mail:czhschc@ 126.com

2014-09-23；

2014-10-29.

广东省青年创新人才项目（No.2014QNCX194）；广东省教改项目（No.GDJG20142402）；潮州市科技计划引导项目（No.2014SF03）

Supported by Project of Education Department of Guangdong（No.2014EQNCX194）；2014 Teaching Reform Project of Higher Education in Guangdong Province（No.GDJG20142402）；Project of Chaozhou Science and Technology Bureau（No.2014SF03）

∗通信联系人，E-mail:dxqzq110@163.com