基于克里格插值法在矿产储量估算中的应用

张树荣　陈琼

[摘要]介绍了克里格插值法的理论基础，结合Quanty Mine软件，论述了克里格插值法应用于矿产储量估算的一般流程，并在某铜锌矿的储量估算中进行了应用。实例验证了克里格插值法可以有效地应用于矿产储量估算，且具有较高的可靠性和精度。

[关键词]克里格插值法；矿产储量；估算

1.引言

随着GIS技术的飞速发展，GIS技术不再局限于地理信息、测绘等传统领域的应用，而是被广泛应用于资源调查、灾害预测、国土管理、城市规划、交通运输、农林牧业等众多领域，而在矿业领域的应用也越来越频繁与深入。

克里格插值法（Kriging）是GIS技术的重要方法之一，又称为空间自协方差最佳内插法，它是地质统计学的主要内容之一，由于地质统计学是基于统计特征的，所以用克里格插值法进行插值可以获得较好的预测结果，因此逐渐在矿产储量估算中得到广泛的应用。本文以紫金矿业集团股份有限公司与中国地质大学联合开发的QuantyMine软件为工具，利用该软件的克里格插值法对某铜锌矿进行储量估算，并与该矿体的地质勘探报告中的储量计算结果进行比较分析。

2.矿产储量估算流程

采用克里格插值法进行矿产储量估算是将整个矿体划分成许多小块段（待估块段），在充分考虑信息样品的形状、大小及其与待估块段相互间的空间分布位置等几何特征以及品位的空间结构之后，对每一信息样品值分别赋予一定的权系数，最后进行加权平均来估计块段品位的方法，从而实现对该矿区储量的总体估算。

采用克里格插值法进行储量估算可以分为三个步骤：第一步建立矿区数学模型，也就是估值模型；第二步利用估值模型进行块段估值：第三步进行储量估算及汇总。

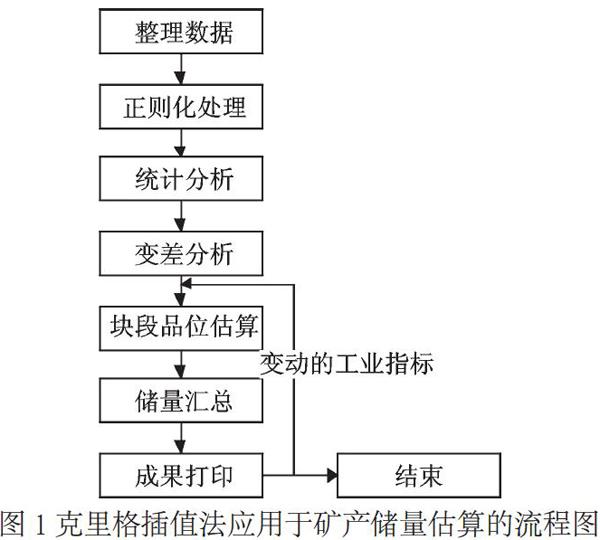
图1显示了采用克里格插值法进行矿产储量估算的大致流程。其中，正则化处理是进行样品等长或等体积处理，形成几何形态基本相似的组合样；统计分析主要是对组合样进行直方分析，拟合满足正态分布的区域化变量；变差分析就是在实验变差函值的基础上进行结构分析，建立块段估值模型，为块段品位计算及矿产储量估算提供数学依据。从图1可以看出，对于动态指标下的矿产储量估算，一旦工业指标发生变动，只需根据新的工业指标重新汇总即可。

3实例分析

矿区是以铜为主的铜锌硫化物矿床，伴有Au、Ag、Pb、Se、S等5种有益矿产，盆地内除已勘查的Ⅰ、Ⅱ号矿体外，尚有规模宏大、分布广泛的矿化蚀变带。本文以Ⅰ号矿体为例，进行矿产储量估算。Ⅰ号矿体总体南北向展布，为半隐伏矿体，矿体主要呈层状，似层状或透鏡状，形态受向斜构造的控制，呈向北倾状、向南扬起、矿体东翼向西倒转的紧闭向斜形态。首先对该矿区进行了地质普查，详查，勘探工作，收集了各类原始资料，满足矿产储量估算对样品数量及分布的要求。

本文以紫金矿业集团股份有限公司与中国地质大学（武汉）联合开发的Quanty Mine软件为工具，选择59个钻孔、264个穿脉工程为基础数据来源，其样品总数为9563，样品品位最大值为17，最小值为0.01，均值为1.99，方差为4.34。

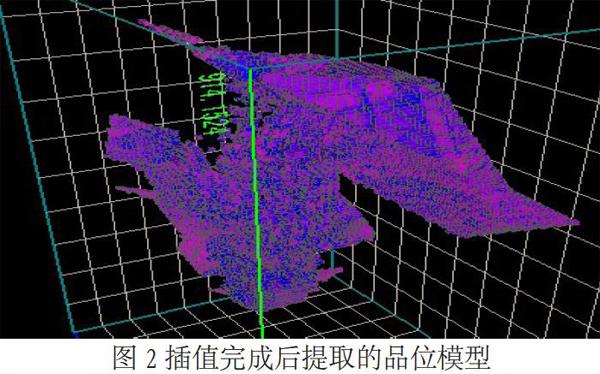
建立品位模型，即使用地质统计学方法根据空间分布的样品数据计算每个块体的平均品位，从而形成矿区矿体的品位模型。图2为采用克里格插值完成后，导入分级范围，对插值结果按品位进行提取查看，并用颜色表示出品位的变化。

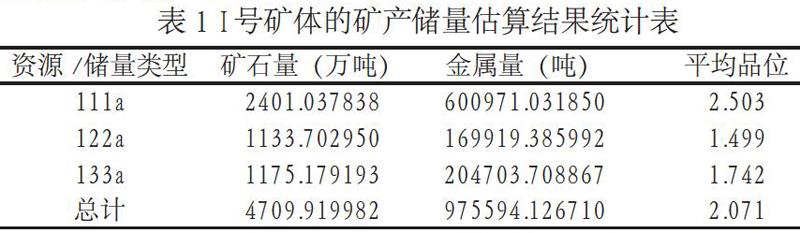
利用储量统计功能对Ⅰ号矿体进行汇总，输出该矿体储量估算结果，并与该矿区勘探工作完成提交的《某铜锌矿区Ⅰ号矿体勘探地质报告》的储量进行对比分析。

1993年-1997年进行Ⅰ号矿体的勘探工作，1998年2月提交了《某铜锌矿区Ⅰ号矿体勘探地质报告》。该地质报告批准的金属量为：974454吨，与本次采用克里格插值法估算出的金属量（975594吨）相差1千多吨，在正常误差范围内。因此，这个估算结果还是比较可靠的。

4.结语

本文以紫金矿业集团股份有限公司与中国地质大学（武汉）联合开发的Quanty Mine软件中的克里格插值功能为工具，对某铜锌矿的Ⅰ号矿体进行了储量估算，估算结果与该矿体的地质勘探报告中批准的储量基本吻合，估算结果较为准确，精度较高。实例验证了克里格插值法可以有效地应用于矿产储量估算，且具有较高的可靠性和精度。