钢桥面板加劲肋焊缝位置热点应力数值分析

傅中秋, 吉伯海, 王满满, 章青

(1.河海大学土木与交通学院,江苏南京210098;2.河海大学力学与材料学院,江苏南京210098)

钢桥面板加劲肋焊缝位置热点应力数值分析

傅中秋1, 吉伯海1, 王满满1, 章青2

(1.河海大学土木与交通学院,江苏南京210098;2.河海大学力学与材料学院,江苏南京210098)

采用8节点单元和20节点单元分别建立钢桥面板U肋焊接部位的有限元分析模型,分析不同单元尺寸划分对模型分析精度的影响,对比两种模型计算差异,并分析不同热点应力取值方法的区别。分析结果表明,随着单元尺寸的减小,顶板表面弯曲应力增大,板厚方向弯曲应力增大。相对而言,20节点单元模型计算结果更容易收敛,对于8节点单元模型建议设置8层单元,20节点单元模型建议设置4层单元。在热点应力的取值方法中,表面外推法结果稳定,表面以下1 mm应力法结果受单元尺寸的影响。

钢桥面板;焊缝;热点应力;有限元模型

正交异性钢桥面板是钢桥面板的主要结构形式,广泛应用于钢桥结构。由于构造复杂,尤其是焊缝位置存在几何突变,易产生应力集中[1]。钢桥面板焊接时,其焊缝质量也会存在各种焊接缺陷,可能导致局部受力突变。在交变荷载的作用下,正交异性钢桥面板焊缝位置易产生疲劳破坏,直接影响桥梁的安全运营[2]。

焊缝位置疲劳损伤主要取决于应力变化[3]。目前针对疲劳损伤的应力存在多种应力代表值取值方法,如名义应力、热点应力、缺口应力等[4]。传统疲劳应力以名义应力法为主[5]。由于热点应力具有较好的精度,实际应用可行,近几年热点应力也被广泛研究和应用[6]。热点应力取值点位于焊缝边缘几何突变位置,无论是计算分析或者实际测试,都难以获得准确的应力值[7]。基于静力加载的计算方法,文中针对顶板焊缝位置的应力进行分析,研究热点应力的分析模型及取值方法,为疲劳损伤数值分析提供参考。

1 分析模型

由于疲劳与局部应力相关,只要模型能反应局部应力变化,可认为能反应该构造细节的疲劳应力情况。文中采用钢桥面板顶板与U肋连接接头局部模型来模拟U肋与顶板焊缝的构造细节,通过在顶板上施加面外荷载,模拟实桥中顶板弯曲受力。尽管U肋的约束条件与实际存在差异,但只要焊缝应力能反应U肋焊缝的疲劳受力情况,可认为该模型是可行的。

模型尺寸如图1所示,U肋与顶板呈78°焊接,焊接形式为半熔透剖口焊,熔透率为75%。顶板上焊脚尺寸与U肋上焊脚尺寸相同,均为6 mm。试件边界约束及加载如图1所示,试件一端固定约束,另一端悬空。盖板与顶板采用螺栓连接,盖板长度为240 mm,宽度为300 mm。均布荷载中线点距固定端边缘240 mm,荷载大小为4 000 N,加载面积如图所示。

采用Ansys软件,分别选用8节点实体单元solid185和20节点实体单元solid186建立桥面板实体单元模型。分析模型如图2所示,沿板厚方向设置多层单元。

2 模型精度分析

2.1 单元划分尺寸影响

分别针对8节点和20节点实体单元模型进行分析,沿板件厚度方向分别设置1,2,3,8,16,24,32层单元。顶板上表面焊根侧应力分布(节点应力)如图3所示。

图2 有限元模型Fig.2 Finite elementmodel

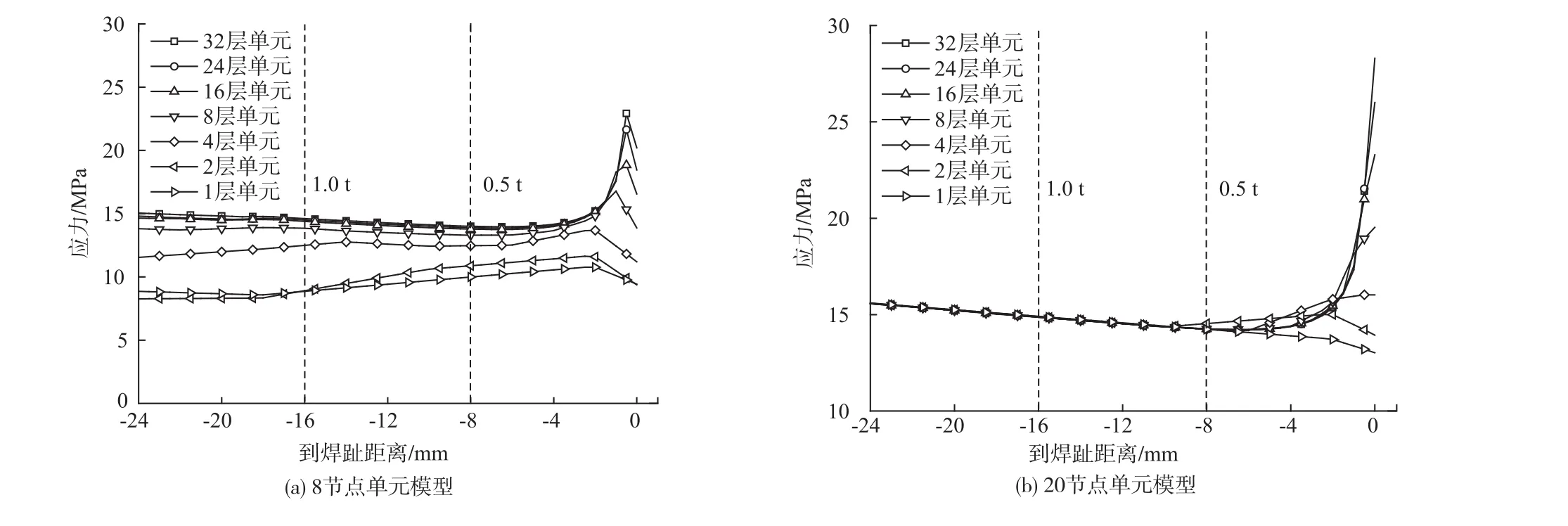
图3 焊根侧顶板表面应力分布Fig.3 Stress of weld root side roof surface

随着单元尺寸的减小,顶板表面弯曲应力增大。对于8节点模型,采用不同单元尺寸时,焊根附近顶板表面应力相差较大。沿板厚方向设置1～4层单元时,焊缝0.25 t～2.0 t范围内应力先减小后增大,与实际应力变化趋势不符。沿板厚方向设置8层以上单元时,应力计算结果较为稳定。对离焊根0.5 t及1.0 t处点的应力,随单元尺寸的减小,应力增大,并逐渐收敛。对于20节点模型,采用不同单元尺寸时,顶板表面距离焊根0.4 t距离以外点的应力相差不大。距离焊根0.5 t以内点的应力因受焊缝的影响,呈非线性增加。沿板件厚度方向设置16层以上单元时,各点应力分布几乎相等,仅在焊根处(0.5 mm距离内)的应力存在差异。

顶板焊根处沿板厚方向应力分布随单元尺寸的变化如图4所示。板厚方向以弯曲应力为主。随着单元尺寸的减小,弯曲应力增大。

对于8节点模型,沿板厚方向设置4层以内单元时,应力沿板厚方向呈线性分布,且应力受单元尺寸的影响较大。沿板厚方向设置8层以上单元时,表面0.1 t以下点的应力稳定,呈线性分布,不受单元尺寸影响。对于20节点实体单元模型,沿板厚方向设置1层单元时,应力沿板厚方向呈直线分布。沿板厚方向设置多层单元时,应力沿板厚方向呈折线形分布,但应力变化不大。焊缝对板厚方向应力的影响范围与采用8节点实体单元计算所得的结果相同,在0.1 t左右。

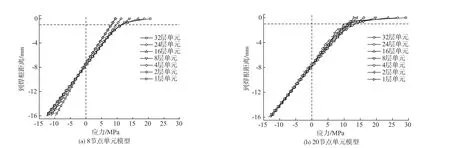
图4 焊根处沿板厚应力分布Fig.4 Distribution of the stress along the thickness direction

2.2 单元类型影响

取沿板厚划分为32层单元8节点和20节点实体单元模型,对比分析焊缝表面应力分布及沿板厚方向应力分布如图5所示。对焊缝附近板表面0.5 t以外的区域,采用20节点实体单元模型计算得到的应力比采用8节点实体单元计算所得的应力大5%左右。在板厚度方向,表面0.5 mm以下区域,采用20节点实体单元计算得到的板厚方向的应力分布与采用8节点实体单元得到的应力几乎相等,仅在板表面至表面以下0.5 mm处的应力存在差异。

图5 不同单元类型模型计算结果比较Fig.5 Com parison of different elementmodels calculation results

3 热点应力取值

3.1 热点应力取值方法

由于焊缝热点位置为焊缝几何边缘位置,受应力集中影响显著。在计算或实际测试时,热点位置的应力值较难准确得到,而离热点应力一段距离位置的应力值计算或实测较稳定[8]。除了某些简单的情况,几乎没有现成的公式来计算结构的热点应力。采用解析法计算复杂结构的热点应力是不可行的,只能采用有限元法或间接测试方法来计算结构的热点应力。对于板结构来说,现有4种方法得到焊趾处的热点应力:

1)表面应力外推法[9]:假设热点往外的应力分布服从函数关系,利用热点外侧2点或3点的应力值和函数关系来倒推处热点位置的应力。国际焊接学会(IIW)已推荐2点3点[10]及表面外推法。

2)沿板厚方向应力线性化法[11]:将板厚方向热点应力可以分解为呈线性分布的膜应力和弯曲应力之和。

3)Dong法[12]:以离焊微小距离(如2 mm)远处的应力为依据,根据平衡条件得到焊趾处的热点应力。此法对网格的划分不敏感,故不对其进行分析。

4)表面以下1 mm应力法(1 mm)[13]:Yamada建议以焊趾处表面1 mm以下点得应力来作为热点应力。对与焊根-顶板裂纹,此方法可消除板厚对热点应力强度的影响。

3.2 热点应力计算结果对比

根据模型精度分析,20节点单元模型应力计算更容易收敛,故应用20节点单元模型进行不同热点应力取值方法的计算。图6为焊根处的热点应力计算结果对比。

由图6可知,采用表面外推法得到的热点应力随网格尺寸的细化而收敛。采用3点表面外推法与2点表面外推法得到的热点应力几乎相等。板厚方向需设置不少于4层单元。采用沿板厚方向积分方法得到的热点应力随网格的细化而收敛,比采用表面外推法得到的热点应力小5%左右,其热点应力值几乎不受单元尺寸的影响。取焊趾处板表面以下1 mm处应力作为热点应力时,随单元网格的细化,应力先增大后减小,较不稳定。当厚度方向取32层单元时,得到的热点应力比表面外推法得到的热点应力小15%左右。

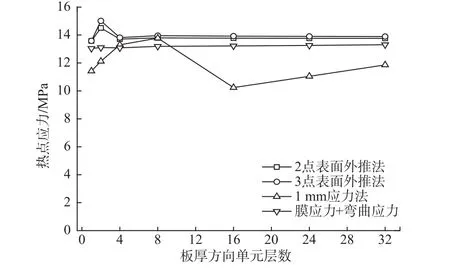
图6 20节点实体单元焊根热点应力计算结果Fig.6 Calcu lation resu lts of hot spot stress at 20 node solid element root

4 结 语

1)随着单元尺寸的减小,顶板表面弯曲应力增大,板厚方向、弯曲应力增大。单元划分尺寸对于8节点单元模型影响比20节点单元模型影响显著, 20节点单元模型计算结果更容易收敛。

2)采用8节点实体单元计算热点应力,板厚方向设置8层单元以上时计算结果可达到取值精度要求;采用20节点实体单元计算热点应力,沿板厚方向设置不少于4层单元时计算结果可达到取值精度的要求。

3)表面外推法结果稳定,2点外推法和3点外推法所计算热点应力值差异不明显,厚度方向积分方法计算值比表面外推法小,表面以下1 mm应力法结果受单元尺寸影响。

[1]张启伟,张鹏飞.正交异性钢桥面板焊接节点应力集中系数[J].同济大学学报:自然科学版,2010,38(10):1428-1433.

ZHANG Qiwei,ZHANG Pengfei.Hot spot stress concentration factor for welded joints in steel orthotropic decks[J].Journal of Tongji University:Natural Science,2010,38(10):1428-1433.(in Chinese)

[2]吉伯海,赵端端,傅中秋,等.车轮荷载下钢箱梁疲劳构造细节应力等级评定[J].河海大学学报:自然科学版,2014,42 (5):416-421.

JIBohai,ZHAO Duanduan,FU Zhongqiu,etal.Fatigue stress level evaluation of structural details of steel box girder underwheel load[J].Journal of Hohai University:Natural Sciences,2014,42(5):416-421.(in Chinese)

[3]王元清,林云,周晖,等.高强度钢材及其焊缝脆性断裂与疲劳性能的研究进展[J].建筑钢结构进展,2012,14(5):21-28.

WANG Yuanqing,LIN Yun,ZHOU Hui,et al.Progress in the brittle fracture and fatigue of high strength steels and their welds [J].Progress in Steel Building Structures,2012,14(5):21-28.(in Chinese)

[4]Hobbacher A F.The new IIW recommendations for fatigue assessment of welded joints and components-A comprehensive code recently updated[J].International Journal of Fatigue,2009,31(1):50-58.

[5]李德勇,姚卫星.缺口件振动疲劳寿命分析的名义应力法[J].航空学报,2011,32(11):2036-2041.

LIDeyong,YAO Weixing.Nominal stress approach for life prediction of notched specimens under vibration loading[J].Acta Aeronautica ET Astronautica Sinica,2011,32(11):2036-2041.(in Chinese)

[6]陈策,吉伯海,徐汉江.钢桥面板闭口加劲肋关键点的热点应力分析[C]//中国土木工程学会桥梁及结构工程分会.第二十届全国桥梁学术会议论文集(上册).北京:人民交通出版社,2012:309-314.

[7]王亚飞,徐海鹰.热点应力法进行钢桥疲劳检算[J].铁道工程学报,2012(9):49-52,58.

WANG Yafei,XU Haiying.Check of steel bridge fatigue with hot spot stressmethod[J].Journal of Railway Engineering Society, 2012(9):49-52,58.(in Chinese)

[8]邵永波.轴力作用下TT节点焊缝周围应力分布规律研究[J].机械强度,2008,30(2):244-249.

SHAO Yongbo.Study of the stress distribution along theweld toe for tubular TT-joints subjected to axial tensile loads[J].Journal of Mechanical Strength,2008,30(2):244-249.(in Chinese)

[9]周张义,李芾.基于表面外推的热点应力法平板焊趾疲劳分析研究[J].铁道学报,2009,31(5):90-96.

ZHOU Zhangyi,LIFu.Study on fatigue analysis of welded toes of plate structures using hot spot stressmethod based on surface extrapolation[J].Journal of the China Railway Society,2009,31(5):90-96.(in Chinese)

[10]Hobbacher A F.Fatigue Design ofWelded Joints and Components[M].Flemington,New Jersey:Whitehurst and Clark,1996.

[11]Niemi E,Tonskanen P.Hot spot stress determination forwelded edge gussets[J].Welding in theWorld,2000,44(5):31-37.(in Chinese)

[12]Dong E A.Structural stress definition and numerical implementation for fatigue analyses[J].International Journal of Fatigue, 2001,23:865-876.

[13]ヤサムオル,山田健太郎,石川敏之.デツキプレ一トとUリブの溶接ビ一ドを貫通する疲労き裂の耐久性評価[J].鋼構造論文集,2009,16(64):11-20.

(责任编辑:杨 勇)

Hot Spot Stress Numerical Analysis of Steel Bridge Deck W eld

FU Zhongqiu1, JIBohai1, WANG Manman1, ZHANG Qing2
(1.College of Civil and Transportation Engineering,Hohai University,Nanjing 210098,China;2.College of Mechanics and Material,Hohai University,Nanjing 210098,China)

The finite elementmodels of bridge deck to U rib welded are established by using 8 node element and 20 node element.Themodel precision influenced by different size division is analyzed.The influence of the element type and hot spot stressmethod to the calculation results were compared.The results show that the bending stress on plate surface and along the thickness direction increaseswhen the element size decreases.In comparison with 8 nodemodel, the calculation result of 20 node elementmodel convergesmore easily.8 layers are suggested to the 8 node element model and 4 layers are suggested to the 20 node elementmodel.By the comparing of different hot spot stressmethods, the value by surface extrapolation method is stable and beneath the surface of 1 mm stressmethod influenced by the element size.

steel bridge deck,weld,hot spot stress,FEM

Email:fumidaut@163.com

U 441+.4

A

1671-7147(2015)03-0333-05

2014-10-29;

2015-01-05。

国家自然科学基金项目(51278166,51478163);江苏省第四期“333高层次人才培养工程”项目。

傅中秋(1983—),男,江苏南京人,副教授,工学博士。主要从事钢桥维护等研究。