一种快速提取植物叶片最小外接矩形的算法
李洋, 李岳阳
(江南大学物联网工程学院,江苏无锡214122)
一种快速提取植物叶片最小外接矩形的算法
李洋, 李岳阳*
(江南大学物联网工程学院,江苏无锡214122)
为了提高提取植物叶片最小外接矩形的计算效率与精确度,提出一种快速提取植物叶片最小外接矩形的算法。该算法首先使用Canny算子提取叶片轮廓,然后使用基于平面扫描法的Graham算法构造叶片轮廓凸包,最后提取叶片最小外接矩形。仿真实验结果表明:在Flavia植物叶片数据库中进行测试,该算法优于旋转法、顶点链码法。
图像处理;最小外接矩形;Graham算法
在植物叶片识别中,叶片形状特征[1]是分类依据之一。其中,矩形度[2](叶片面积与叶片最小外接矩形(MER)的面积之比)是重要的形状特征参数。最小外接矩形的长宽即为植物叶片的长宽,叶片长宽比值不仅可以作为植物分类的一个特征,而且能够及时了解植物的生长发育情况,对农作物的栽培和管理具有重要的参考价值。因此,提取植物叶片最小外接矩形具有重要的意义。
国内研究者普遍采用旋转法[3-4]与顶点链码法[5-7]提取目标图像最小外接矩形。随着计算机视觉领域的不断发展,相关研究已逐步展开。卢蓉等[8]利用顶点链码与离散格林理论相结合的方式提取目标图像的最小外接矩形;陈华[9]基于现有软件AutoCAD,通过二次开发确定任意形状物体最小外接矩形;张法全等[10]利用重心原理寻找主轴法提取目标图像的最小外接矩形;苑玮琦等[11]运用矩的测量方法提取植物叶片最小外接矩形。然而,现有方法都存在计算量大,精确度不高等缺点。
因此,文中基于平面扫描法的Graham算法,提出了一种快速的提取植物叶片最小外接矩形的算法。相比一些已有算法,该算法有更快的计算速度。
1 提取最小外接矩形的常用算法
1.1 旋转法
旋转法是将图像中的目标在90°范围内等角度间隔地旋转,每次记录其坐标系方向上的外接矩形参数,取其中面积最小的矩形并记录其长度和宽度。旋转目标法原理简单、适用性广,但计算量大且偏差较大。
1.2 顶点链码法
顶点链码法用方形点阵的八近邻顶点链编码处理二值图像,跟踪边界得到图像边界的顶点链码表,通过解码将其转化为顶点的x方向和y方向的坐标,从x方向坐标和y方向坐标中搜索出最大和最小坐标。以此两点连线作为对角线的矩形即为图像区域的最小外接矩形。顶点链码法虽然运算速度比旋转法快,但仍然存在计算量较大的问题。
2 提取最小外接矩形算法
图1为文中算法的流程图,分3步进行。首先利用Canny边缘检测算子提取叶片轮廓点,再用基于平面扫描法的Graham算法构造叶片凸包,最后利用叶片凸包求最小外接矩形。

图1 文中算法流程Fig.1 Flow chart of the proposed algorithm
2.1 边缘检测Canny算子提取叶片轮廓
由于形状特征建立在叶片轮廓的基础上,因此在提取特征之前,用边缘检测Canny算子检测算子提取轮廓。叶片的轮廓是叶片自身的像素子集,含有丰富的形态信息。边缘是图像中局部灰度发生突变的地方,边缘检测是许多图像处理操作(如图像分割、目标识别、图像匹配和图像分类等)的基础,其检测质量在很大程度上决定了这些后续操作的效果[12]。1986年Canny提出了基于最优化算法的边缘检测算子,总结出著名的Canny边缘检测三准则[13]:信噪比准则、定位精度准则、单边响应准则。
图2是Canny边缘检测的算法流程,其算法过程可描述如下:
1)高斯平滑。用高斯滤波器对原始叶子图像进行平滑处理,可以抑制噪声,Gauss滤波器函数:
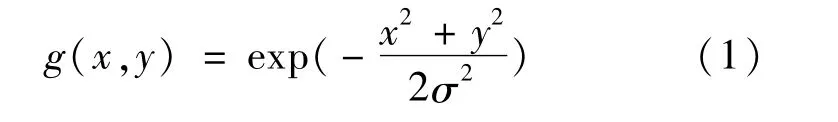
2)梯度计算。计算滤波后图像中每个像素梯度的幅值M(i,j)和方向θ(i,j),采用2×2的模板P和Q分别对x和y方向的一阶偏导数近似:
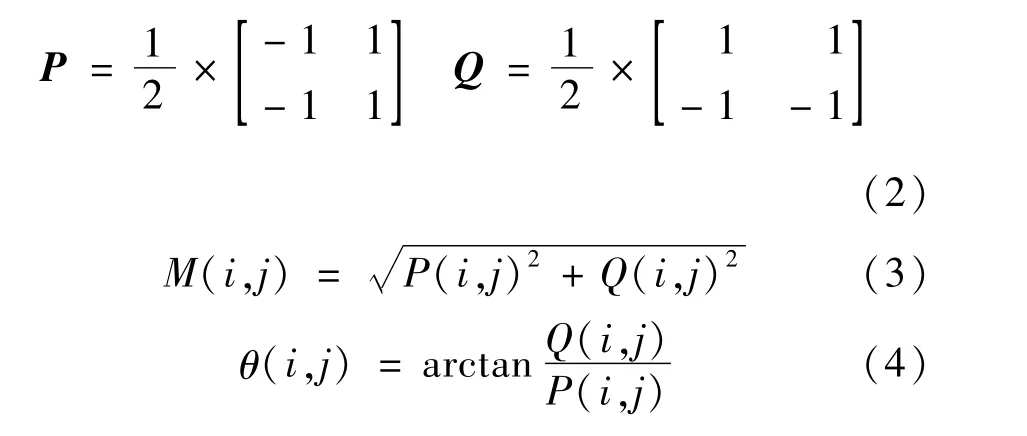
3)非极大值抑制。对图像中的像素点(i,j)处幅值M(i,j)利用梯度方向计算邻域内的幅值,幅值若是梯度方向上非最大值点时则为零,反之即为边缘。
4)双门限检测。使用累计直方图计算两个阈值,凡是大于高阈值的一定是边缘,凡是小于低阈值的一定不是边缘。如果检测结果大于低阈值而小于高阈值,那就要看这个像素的邻接像素中有没有超过高阈值的边缘像素,如果有即为边缘。

图2 Canny算法流程Fig.2 Flow chart of the Canny algorithm
2.2 基于平面扫描法的Graham算法构造叶片轮廓凸包
在提取叶片轮廓后,用基于平面扫描法的Graham算法[14]构造叶片凸包,对叶片边缘做了大量缩点处理。由于2.1中得到的叶片轮廓已消除图像噪声影响,仿真实验显示,此步缩点处理对噪声有很强的鲁棒性。设S(p1,p2,…,pn)是平面上的一个点集,封闭S中所有顶点的最小凸多边形,称为S的凸包。凸包作为物体外形的简单描述工具,提取凸包特征在模式识别领域具有广泛的应用[15],凸包算法也是计算几何重要的研究问题之一。基于平面扫描法的Graham算法构造叶片凸包,其算法过程可描述如下:
1)排序。将点集S按先x坐标再y坐标的字典序,升序排序得到S(p1,p2,…,pn)。则p1与pn必然是凸包上的顶点,可以分成上下两条链分别构造凸包。
2)构造凸包下链。设点A(x1,y1),B(x2,y2), C(x3,y3)是平面上的任意3点,定义方向矩阵D,当 D为正时,ABCA构成一个逆时针方向的回路,即ABC是“左转”;当D为负时,ABCA构成一个顺时针方向的回路,即ABC是“右转”;当D为零时,此时3点共线。
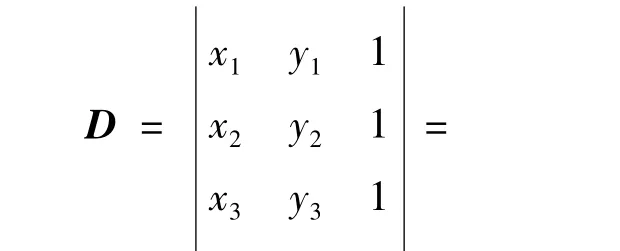
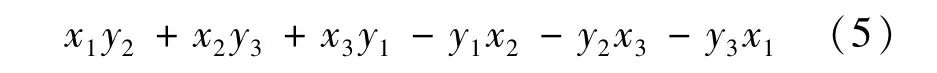
建立一个栈,初始时p1,p2,p3进栈,然后从小到大处理排序后的点列以构造凸包下链。对于pi,若栈顶的两个点与它不构成“左转”的关系,则将栈顶的点出栈,直至没有点需要出栈以后,再将当前点进栈。所有点处理完之后,栈中保存的点就是凸包的下链。图3是在构造过程中的凸包,当末尾加上新的顶点后,可能会破坏凸性,此时只要将凹的部分的点从末尾删除。

图3 构造凸包下链Fig.3 Construct the downchain of the convex hull
3)构造凸包上链。构造上链与2)构造下链不同之处在于从大至小依次处理,由于p1在上下链都一定会出现,构造完成上链后删除最后一点。
2.3 提取叶片最小外接矩形
得到叶片凸包后,就可提取叶片最小外接矩形。一个凸多边形的最小外接矩形必定过该凸边形的一条边,遍历叶片轮廓凸包上的每条边,以该边构造矩形并计算该矩形面积,比较所有矩形的面积,其中面积最小的矩形即为该叶片最小外接矩形。其过程可详细描述如下:
1)随机选取叶片轮廓凸包中一条边AB作为起始边,并分别以点A(x1,y1),B(x2,y2)为左右端点。以A为中心旋转θ角度,使该边平行于坐标横轴,其中旋转角度θ可由下式求得:

2)叶片凸包上的所有点都需绕点A(x1,y1)旋转θ角度。设叶片凸包上的任一点为(x0,y0),旋转后,该点新位置(x,y)可由下式求得:


3)以AB为一个上(下)边界,找到y值最小(最大)的一个点,经过此点作一条平行于x轴的直线,就确定了对应的一个下(上)边界。然后找到x值最小和最大的左侧点和右侧点,经过这两个点分别做垂直于x轴的两条直线,就确定了对应的左边界和右边界。这样即可得到一个外接矩形,计算并保存边AB、旋转角度θ、由该边得到外接矩形的顶点坐标和面积。
4)顺序选择下一条边BC,如果凸包上此边已经选择则转入5),否则跳转至1)并且以BC作为起始边,重复以上的步骤。
5)比较所有外接矩形的面积,找出其中面积最小的外接矩形,按3)中记录的旋转角度和边旋转还原叶片,所得的最小外接矩形的长宽即为叶片的长度和宽度。
3 仿真实验结果及分析
在实验中,使用Flavia植物叶片数据库作为数据集[16],该数据集中有32类植物叶片的样本,每类样本50~77张不等。实验平台为VC++2010,实验测试了Flavia植物叶片数据库中所有数据。图4是对编号为3 044的叶片进行最小外接矩形提取的各阶段实验结果。
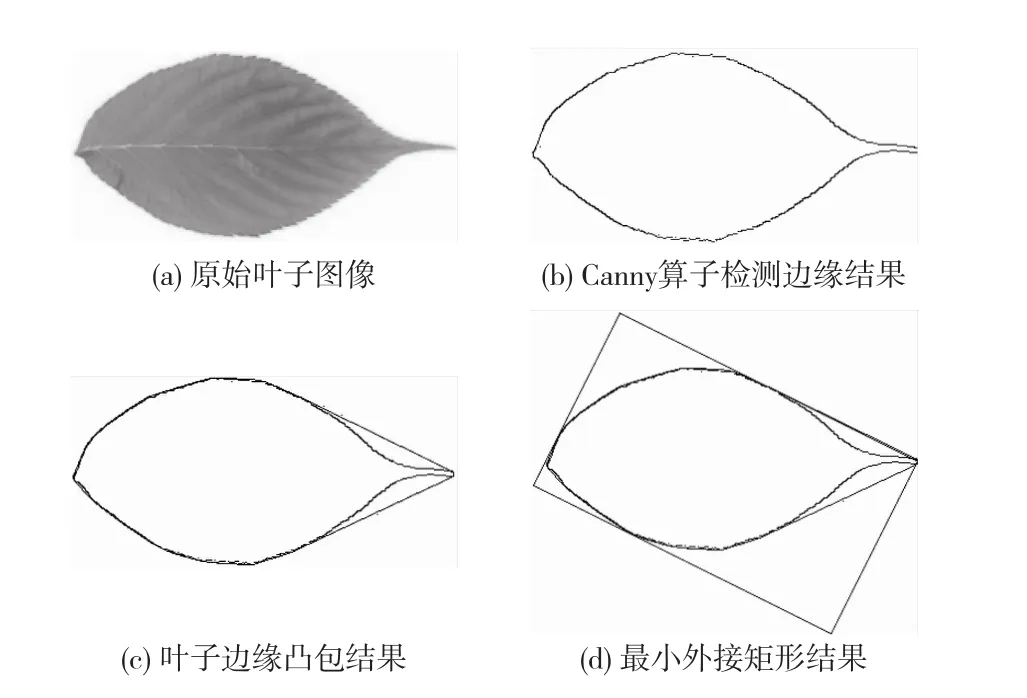
图4 文中算法各阶段实验结果Fig.4 Results of different procedures based on the proposed algorithm
图5为数据集中编号为1 124的叶片。在32类叶片中,其中有19类叶片,采用文中算法、旋转法、顶点链码法所提取的最小外接矩形一致。可以看出,当叶片轮廓比较平滑,轮廓特征比较明显时,3种算法提取结果相同。

图5 3种算法提取叶片1 124的M ER对比Fig.5 Com parison of the MERs obtained by the three algorithm s for leaf 1 124
图6为数据集中编号为3 556的叶片。在32类叶片中,其中有13类叶片采用旋转法提取的最小外接矩形面积比文中算法大,而文中算法和顶点链码法结果一致。可以看出,当叶片边缘比较突兀,轮廓特征不太明显时,文中算法得到的最小外接矩形面积比旋转法小,与顶点链码法结果仍然一致。
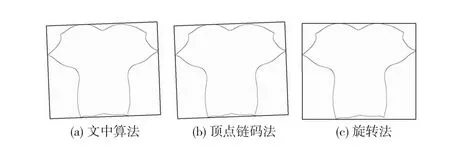
图6 3种算法提取叶片3 556的M ER对比Fig.6 Com parison of the M ERs obtained by the three algorithm s for leaf 3 556
图7为3种算法提取最小外接矩形所需时间的对比结果。图中各算法所示的时间为Flavia植物叶片数据库中各类叶片计算耗时的平均值。
由图7可以看出,旋转法计算时间最长,其次是顶点链码法,文中算法耗时最少。所以,文中算法在计算速度上有明显优势。
图8是采用文中算法所得最小外接矩形与采用旋转法、最小外接矩形的面积之差及文中算法与顶点链码法面积之差对比。
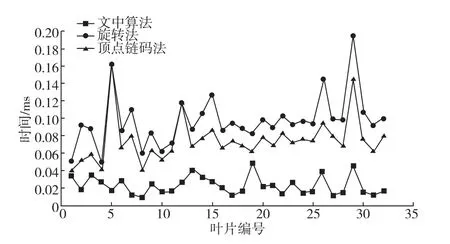
图7 3种方法计算时间对比Fig.7 Com parison of the calculating time of the three algorithm s

图8 文中算法所得M ER与旋转法、顶点链码法所得M ER面积差Fig.8 Area differences of the MERs between the p roposed algorithm,the rotation algorithm and vertex chain code algorithm
由图8可以看出,文中算法在提取最小外接矩形的精确度上相比于旋转法具有明显优势。
4 结 语
文中提出了一种快速提取植物叶片最小外接矩形的算法,该算法首先利用Canny算子提取叶片轮廓,再采用基于平面扫描法的Graham算法构造叶片凸包,最后利用叶片凸包点提取最小外接矩形。仿真实验结果表明,本文算法是一种有效的提取植物叶片最小外接矩形的算法。
[1]魏蕾,何东健,乔永亮.基于图像处理和SVM的植物叶片分类研究[J].农机化研究,2013,5(5):12-15.
WEILei,HE Dongjian,QIAO Yongliang.Plant leaves classification based on image processing and SVM[J].Journal of Agricultural Mechanization Research,2013,5(5):12-15.(in Chinese)
[2]王怡萱,阚江明,张俊梅,等.基于VC++的植物种类模式识别系统研究[J].湖南农业科学,2011(23):131-135.
WANG Yixuan,KAN Jiangming,ZHANG Junmei,et al.Pattern recognition system for plant species based on VC++[J]. Hunan Agricultural Sciences,2011(23):131-135.(in Chinese)
[3]汤晓东,刘满华,赵辉,等.复杂背景下的大豆叶片识别[J].电子测量与仪器学报,2010,24(4):385-390.
TANG Xiaodong,LIU Manhua,ZHAO Hui,et al.Soybean leaves recognition of images with complicated background[J].Journal of Electronic Measurement and Instrument,2010,24(4):385-390.(in Chinese)
[4]林玉池,崔彦平,黄银国.复杂背景下边缘提取与目标识别方法研究[J].光学精密工程,2006,14(3):509-514.
LIN Yuchi,CUIYanping,HUANG Yinguo.Study on edge detection and target recognition in complex background[J].Optics and Precision Engineering,2006,14(3):509-514.(in Chinese)
[5]吴晓光,王涤琼,盛慧.一种获取图像区域最小外接矩形的算法及实现[J].计算机工程,2004,30(12):124-125.
WU Xiaoguang,WANG Diqiong,SHENG Hui.An algorithm and implementation for obtainingminimum exterior rectangle of image region[J].Computer Engineering,2004,30(12):124-125.(in Chinese)
[6]刘玉珍,刘润涛.简单多边形的最小外接矩形算法[J].哈尔滨理工大学学报,2008,13(2):5-7.
LIU Yuzhen,LIU Runtao.An algorithm forminimal circumscribed rectangle of a simple polygon[J].Journal Harbin University of SCIand Tech,2008,13(2):5-7.(in Chinese)
[7]陈优广.边界跟踪、区域填充及链码的应用研究[D].上海:华东师范大学,2006.
[8]卢蓉,范勇,陈念年,等.一种提取目标图像最小外接矩形的快速算法[J].计算机工程,2010,36(12):178-181.
LU Rong,FAN Yong,CHEN Niannian,et al.Fast algorithm for extracting minimum enclosing rectangle of target image[J]. Computer Engineering,2010,36(12):178-181.(in Chinese)
[9]陈华.确定任意形状物体最小包围盒的一种方法[J].工程图学报,2010,31(2):49-53.
CHEN Hua.A method to generate the minimum bounding boxes for shape-arbitrary objects[J].Journal of Graphics,2010,31 (2):49-53.(in Chinese)
[10]张法全,王国富,曾庆宁,等.利用重心原理的图像目标最小外接矩形快速算法[J].红外与激光工程,2013,42(5): 1382-1387.
ZHANG Faquan,WANG Guofu,ZENG Qingning,et al.New algorithm forminimum enclosing rectangle of the object in the image region based on center-of-gravity principle[J].Infrared and Laser Engineering,2013,42(5):1382-1387.(in Chinese)
[11]苑玮琦,胡迪.利用矩实现植物叶片长宽的测量[J].计算机工程与应用,2013,49(16):188-191.
YUANWeiqi,HUDi.Measurementof leaf blade length and width based onmoment[J].Computer Engineering and Applications, 2013,49(16):188-191.(in Chinese)
[12]罗海驰,李岳阳,孙俊.基于ANFIS的图像边缘检测算法[J].江南大学学报:自然科学版,2014,13(5):523-530.
LUO Haichi,LIYueyang,SUN Jun.Edge detecting algorithm for images based on ANFIS[J].Journal of Jiangnan University: Natural Science Edition,2014,13(5):523-530(in Chinese)
[13]邹福辉,李忠科.图像边缘检测算法的对比分析[J].计算机应用,2008(28):215-219.
ZOU Fuhui,LIZhongke.Performance comparison of image edge detection algorithms[J].Journal of Computer Applications,2008 (28):215-219.(in Chinese)
[14]刘宏兵,邬长安,周文勇.基于二维凸包的TSP算法[J].计算机工程与设计,2009,30(8):1954-1956.
LIU Hongbing,WU Changan,ZHOUWenyong.TSP algorithm based on two dimensional convex hull[J].Computer Engineering and Design,2009,30(8):1954-1956.(in Chinese)
[15]吴文周,李利番,王结臣.平面点集凸包Graham算法的改进[J].测绘科学,2010,35(6):123-125.
WUWenzhou,LILifan,WANG Jiechen.An improved Graham algorithm for determining the convex hull of planar points set[J]. Science of Surveying and Mapping,2010,35(6):123-125.(in Chinese)
[16]王艳菲.基于CENTRIST的植物叶片识别算法研究及移动平台上的实现[D].杨凌:西北农林科技大学,2012.
(责任编辑:邢宝妹)
Fast A lgorithm for Extracting M inim um Enclosing Rectangle of Plant Leaves
LIYang, LIYueyang*
(School of Internet of Things Engineering,Jiangnan University,Wuxi214122,China)
In order to improve the extraction efficiency and accuracy,a fast algorithm is proposed to extract the minimum enclosing rectangle(MER)of plant leaves.Using the canny edge detection operator to extract the contour of leaves,the Graham algorithm based on the flat plane scanning is applied to construct the convex hull of the leaf contour,the MER is extracted.The effectiveness of the proposed algorithm is verified by using the Flavia plant leaf database and the experimental results show that it is better than the rotation algorithm and vertex chain code algorithm.
image processing,minimum enclosing rectangle,Graham algorithm
TP 751
A
1671-7147(2015)03-0273-05
2014-12-30;
2015-02-26。
国家自然科学基金项目(61170119);中央高校基本科研业务费专项基金项目(JUSRP211A38)。
李洋(1991—),男,湖北天门人,计算机技术专业硕士研究生。
*通信作者:李岳阳(1973—),男,江苏江阴人,副教授,硕士生导师,工学博士。主要从事人工智能、图像处理等研究。Email:lyueyang@jiangnan.edu.cn

