巧用数学活动解决数学问题

陈坤孝

中图分类号：G633.6 文献标识码：A 文章编号：1002-7661（2015）20-0077-02

哲学让我们知道，没有实践的理论是空洞的理论，没有理论的实践是盲目的实践，中学数学充分体现了从实践到理论，再从理论到实践的认知过程和用知过程，本文中我主要选择了数学中的应用题、排列与组合问题、公理证明三方面的知识的教学进行论述，旨在和老师们探讨一下通过开展数学活动来解决数学问题的必要性。

一、在数学活动中解应用题

解应用题是中学数学的重要组成部分，它充分体现了数学知识在实践中的重要作用，对培养学生的逻辑思维能力、空间想象能力和探究能力都有很好的作用。因此，根据应用题的特点、来源和实用范围开展实践教学活动是很有必要的。

问题1：甲乙二人在长400米的环行跑道上跑步，他们同向而行，甲每秒钟跑6米，乙每秒钟跑4米，甲在乙后100米，若他们同时起跑，问：经过多少时间，甲、乙二人第二次相遇？

分析：这道题对于少部分学生可能难度不大，但对于大多数学生来说还是有一定难度的。教师又是画图又讲解，仍然有一部分人听不懂，其关键就是找不出等量关系。此时，我们不妨来做做这样的实践活动：由学生在班上推荐两位同学，平时活泼好动的做甲，诚实稳重的做乙，来操场上做演示，要求甲快一些，乙慢一些，教师让同学们记住：甲、乙的起点；甲、乙间的距离S=100米；第一次相遇的地点；第二次相遇的地点；当甲第二次追上乙时，教师让他们都站着别动，问：

当甲第一次追上乙时，甲比乙多跑了多少米？（S=100米）。

当甲第二次追上乙时，甲比乙又多跑了习米？学生观察思考后答：一圈=400（米）。

（3）从起跑到甲第二次追上乙，甲一共多跑了多少米？

100+400=500（米）

你能说出此题的等量关系吗？

S甲-S乙=100+400

这样只要学生知道速度、路程、时间的关系，让学生设未知数列方程已变得很轻松了。

当然如果要把行程问题上成实践课，教师在备课前需要作充分的准备，可把同一直线上的追击问题、相遇问题，以及环形道上的相遇与追击问题各出一题提前给学生做，然后教师准备用1～2课时来完成此活动以及课后的相应习题，在以后遇到相应的问题时，他们也就能轻松地解题了，正所谓“磨刀不误砍柴工”。

其实，除了上述的行程问题外，还有许多应用题也可以让学生在自己的实践生活中学习，比如浓度问题、市场营销问题、工程问题、银行存款问题，这些都是无处不在的数学，学生除了向教师学习之外，还可以向自己的长辈们和其他人学习这些知识，学生有了这些基础之后，我想课堂上将会多一些轻松愉快，少一些愁眉苦脸。

二、在数学活动中初步学习组合知识

排列与组合知识虽然初中和小学没有专门作为一个单元来安排，但小学和初中其实都已涉入了，并且此类题对学生来说往往也都是难题，学好这些初步知识对升入高中的学生是很有帮助的，并且也是九年义务教育后对毕业生的基本要求，那么用什么方法能帮助学生认识和理解排列组合知识呢？数学实验和数学活动方法是比较有效的方法之一。

问题2：（1）有10位好朋友相遇了，他们都要彼此握手一次，问，他们一共握了几次手？如果是60位朋友也要彼此握一次手的话，他们又握了几次手？n个人呢？（n≥2）。

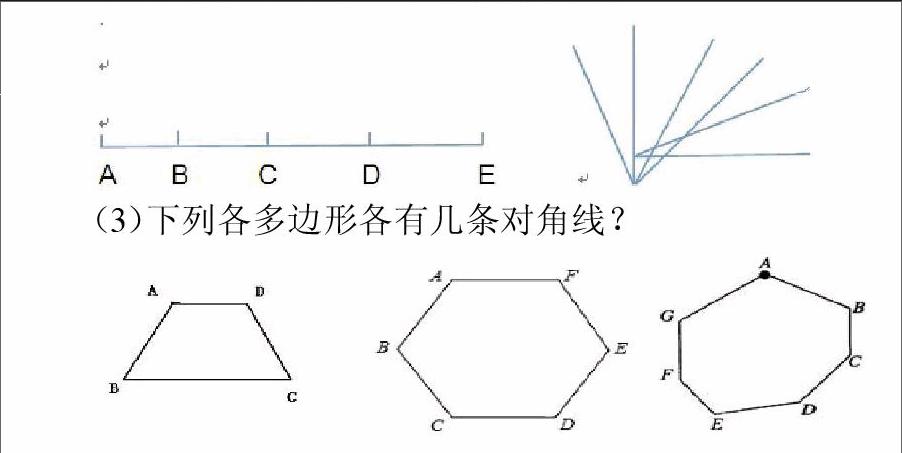
下列图形中各有几条线段或几个角？

（3）下列各多边形各有几条对角线？

分析：上述三类问题虽然是在初中的问题，其实质是高一的组合问题，怎么样让初中生也能初步学会此类简单问题的解法呢？我在上课时做了如下实验，这里只是对第（1）题作叙述；第（2）（3）题由学生画图归纳后，教师作指导。

第一步：让10位学生上讲台站成一排报数。

第二步：让第一位开始出列握手，握完即回到座位，记住自己握了几次手（9）次。然后顺次出列握手，每位同学都记住共握了几次手（9）次；与此同时，台下的学生和老师也数他们握手的次数，当握完时，他们共握了9+8+7+6+5+4+3+2+1=45次。

第三步：握手者每人握了几次？（都是9次）。照这样算应当握了9€？0=90次，而实际只握了45次，到底错在了哪里？由学生讨论、思考后，找出错误原因，当甲与乙握手的时候，甲算了一次，乙也算了一次，这样实际每握一次手都多算了一次，即重复了一次，因此正确的算法是（9€？0）€？=45（次）。活动到此，教师问：60个好朋友又握了几次手呢？绝大多数都能准确地计算：[（60-1）€？0]€？=1770（次），教师进一步讲解：因为60个人握手。每个人都握了59次，但由于每握一次手都多算了一次，因此实际握手的次数为[（60-1）€？0]€？=1770（次）。n个人握手的次数：次，（由学生归纳得出）。

对于上述的第（2）题，它的解法与第一题完全相同。

第三小题：教师要引导学生弄清：从n边形的一个顶点出发，最多能画（n-3）条对角线，这样，n边形的对角线的条数（N）为：N=（n≥3）。

三、在数学活动中学习“公理”

所谓公理，它是人们在长期的生产实践和生活中总结出来的道理，用大众的话说它是一种经验，但这种经验必须是对的才称它为公理，由此可见，公理来自于生产实践，数学教学是一个“再认识，再创造”的过程，学生只有充分认识了知识的形成过程，理解了知识，进而上升为自己的理论，才算是真正掌握了知识，所以，用实验或活动来教学也是比较符合认知规律的一种方法。

总之，从数学的来源与数学的最终目标来看，数学知识最初都来源于生活实践，通过推理、抽象概括成为数学理论，最终这些理论又被应用于生活与实践，服务于社会、生产与生活，引导学生在实践中学会学习，学到数学知识，并在实践中应用知识都是数学学科最根本的要求。数学活动形象、生动，它丰富了学生的数学生活，加强了对基础知识的理解，增强了学生的空间观念。如果我们能做到“因材施教”和“因人施教”，选取恰当的数学活动，让学生在实践或活动中去做、去尝试和创新，就能够培养学生的实践能力和创新能力，提高教育教学质量。

（责任编辑 文 思）