Numerical estimates of the maximum sustainable pore pressure in anticline formations using the tensor based concept of pore

pressure-stress coupling

Andreas Eckert*,Weicheng Zhang,Xiaolong Liu,Matthew Paradeis

Department of Geosciences and Geological and Petroleum Engineering,Missouri University of Science and Technology,Rolla,MO,USA

1.Introduction

Subsurface engineering applications such as waste water disposal,CO2geological sequestration and hydrocarbon production involving the injection of fluids cause a change in pore fluid pressure,which in turn affects the in situ effective state of stress in the subsurface.The selection of suitable injection sites depends critically on the assessment of geomechanical risks such as fracture reactivation associated with the pore pressure increase(e.g.Streit and Hillis,2004;Li et al.,2006;Rutqvist et al.,2007,2008;Vidal-Gilbert et al.,2008;Cappa and Rutqvist,2011;Zoback,2012).Sibson(2003)showed that hydraulic extensional fractures are only critical for intact rock at low differential stress and that the reactivation of cohesion less,optimally oriented shearfractures determines the lower limit of sustainable reservoir overpressures.These fractures,if critically stressed,represent fluid flow pathways(Barton et al.,1995)along which injected fluids such as dissolved CO2may escape into the atmosphere or into freshwater aquifers.If such fractures are reactivated due to fluid injection applications,seismicity with moment magnitudes ranging from-3 to 5 can be observed(e.g.Gibbs et al.,1973;Wesson and Nicholson,1987;Frohlich et al.,2010;Cappa and Rutqvist,2011;Verdon et al.,2011).

Whilst a general understanding of the physical process resulting in fracture reactivation and seismicity exists,for a detailed sitespecific risk assessment,extensive time-consuming numerical modeling studies coupling fluid flow simulation through porous media with a geoemchanical analysis are necessary to evaluate these risks(e.g.Settari and Mourits,1998;Minkoff et al.,2003;Dean et al.,2006;Rutqvist et al.,2007;Vidal-Gilbert et al.,2008;Cappa,2011;Cappa and Rutqvist,2011).As a major conclusion from such studies,the prevailing stress regime(Rutqvist et al.,2007,2008;Paradeis et al.,2012)and the fluid flow boundary conditions(Rutqvist et al.,2007;Zhou et al.,2008;Amirlatifi et al.,2012)are the most critical parameters.However,with respect to waste water disposal operations,a study by the National Research Council(NRC,2012)concluded that data on fault locations,size and fault properties,in situ stress,and rock properties are often notsufficient to be supplemented to existing numerical models with accuracy on a site-specific basis.

As a means to counter such disadvantages,simplified analytical techniques can be used as a pre-injection risk estimate for fault reactivation.The principle of pore pressure-stress coupling(Engelder and Fischer,1994;Hillis,2001)can be used to estimate the maximum sustainable pore pressure,Pc,(e.g.Wiprut and Zoback,2000;Streit and Hillis,2004;Rutqvist et al.,2007)for sites where limited geological knowledge exists.Pore pressurestress coupling is based on the observation that the total minimum horizontal stress changes with a change in pore pressure(Teufel et al.,1991).However,recent studies by Altmann et al.(2010,2014)showed that pore pressure-stress coupling does affect not only the minimum horizontal stress but also all components of the principal stress tensor and is a complex function of space and time.Altmann et al.(2014)indicated that pore pressurestress coupling is therefore different for each stress regime.For the risk of fault reactivation in a homogeneous full space,Altmann et al.(2014)concluded that for strike-slip and compressional stress regimes,the fault reactivation risk is the highest along theσHdirection.For extensional stress regimes,the fault reactivation risk is the highest along theσVdirection.Therefore,a thorough understanding of the state of stress at potential fluid injection sites is necessary.

Often numerical modeling studies of fluid injection scenarios are simplified to a horizontally layered sedimentary basin(Li et al.,2006;Rutqvist et al.,2007,2008;Zhou et al.,2008;Cappa and Rutqvist,2011).These simplified model geometries are valuable to study the influence of parameters such as permeability,injection rate, fluid flow boundary conditions and seal efficiency on CO2plume spreading and pressurization(e.g.Zhou et al.,2008;Ehlig-Economides and Economides,2010;Cappa and Rutqvist,2011).A geomechanical risk assessment simulating an accurate representation of frequently heterogeneous in situ state of stress requires model geometries reflecting the actual geological scenario and thus considering the mechanical contribution arising from geometrical heterogeneities(Rutqvist et al.,2008;Amirlatifi et al.,2012;Paradeis et al.,2012).In this regard,anticline structures are among the most common structural traps for hydrocarbon reservoirs and thus become a prime target of the emerging challenge of safe geological sequestration of CO2(Metz et al.,2005)and waste water disposal.CO2sequestration in anticline structures has been investigated by Paradeis et al.(2012)and Amirlatifi et al.(2012).Amirlatifi et al.(2012)performed a fluid flow simulation analysis based on generic anticline geometries and showed that low amplitude,large wavelength anticline structures provide the best conditions for CO2sequestration.They also concluded that the fluid flow boundary conditions are of utmost importance when evaluating geomechanical risks due to fluid injection.Paradeis et al.(2012)utilized the same generic model geometries and performed a finite element based pre-injection risk assessment by calculating the critical pore pressure increase based on the geometrical factors of anticline wavelength and amplitude and the prevailing stress regime.Using a simplified analytical solution neglecting pore pressure-stress coupling,they concluded that the stress regime is the most critical factor and that for extensional and strike-slip stress regimes,anticline structures provide safer conditions than horizontally layered basins.

In addition to the anticline geometry and the stress regime,the friction coefficient between bedding layers and its impact on critical sustainable pore pressures,and the resulting risk of fault reactivation merit special consideration.Flexural slip between sedimentary layers accommodates the strain during multi-layer folding and it has been shown that the presence or absence of interlayer slip strongly controls the distribution and evolution of strain within folded strata(Smart et al.,2009)and thus has a significant impacton fracture reactivation(Sanz et al.,2008;Smart et al.,2009).The friction coefficient between bedding planes effectively describes the coupling between different layers,whereby a low friction coefficient represents a weak coupling and a high competence contrast between adjacent layers is produced(Twiss and Moores,2007).A large friction coefficient represents a strong coupling and hence different friction values should result in different stress and strain distributions across adjacent bedding layers.

In this study,three-dimensional(3D) finite element models of generic anticline geometries are utilized to simulate the heterogeneous state of stress.Based on the advanced,tensor based principle of pore pressure-stress coupling(Altmann et al.,2014),analytical equations of the maximum sustainable pore pressure change,ΔPc,are derived to perform a pre-injection geomechanical analysis to assess the fault reactivation risk for different stress regimes.In addition,the influence of the interbedding coefficient of friction and the Young’s modulus contrast between injection layer and cap rock are investigated for different locations in the anticline structure.The analysis is based on the long-term limits given by Altmann et al.(2010),which become especially relevant for subsurface engineering applications such as CO2sequestration and waste water disposal which are interested to estimate how much pore pressure change is sustainable over long times.

Fig.1.Different stress components,σ1,σ2,and σ3,in the principal axis coordinate system can be represented as radial and tangential stresses along different axes with respect to the injection location(after Altmann et al.,2010).

2.Theoretical background

2.1.Pore pressure-stress coupling

Based on the solution of continuous fluid injection obtained by Rudnicki(1986),Altmann et al.(2010,2014)showed that pore pressure-stress coupling,i.e.the ratio of Δσij/ΔP,is a complex function of space and time and has tensor character.This means that all components of the principal stress tensor are affected by changes in pore pressure,contradictory to the previous concept described by Engelder and Fischer(1994)and Hillis(2001).The complex nature of the pore pressure-stress coupling function can be simplified by considering the long-term limits.When t→∞,the coupling ratios for the radial and tangential stress components with respect to the injection location in a principal stress coordinate system(Fig.1,after Altmann et al.,2010)can be derived.For the radial stress,the coupling ratio matches the solution of Engelder and Fischer(1994)without using any of their assumptions(Altmann et al.,2010,2014):

where α represents the Biot coefficient and νthe Poisson’s ratio.

For the tangential stress,the coupling ratio is given by(Altmann et al.,2010,2014):

Based on these long-term limits,the effective principal stress tensor after a change in pore pressure,ΔP,can be calculated(Altmann et al.,2014).If the effective state of stress prior to fluid injection/depletion is given by the radial effective stress,σ′rad,and the tangential effective stress,σ′tan,a pore pressure change,ΔP,due to fluid injection results in the new effective stresses,σ′andσ′

tan:rad stress after a pore pressure change is also derived.The following derivations are given for the general case involving principal stresses,σ1,σ2and σ3.To obtain results for the specific stress regimes where the principal stresses are given by the vertical stress,σV,and the two horizontal stresses,σhand σH,corresponding order of the principal stresses has to be used,i.e.for a compressional stress regime,σ1= σHand σ3= σV.

(1)Along σ3direction:according to Fig.1 and Eq.(4),σ3then represents the radial principal stress andσ1the tangential principal stress.The Mohr-Coulomb criterion is then given by

which includingΔP=Pc-P becomes:

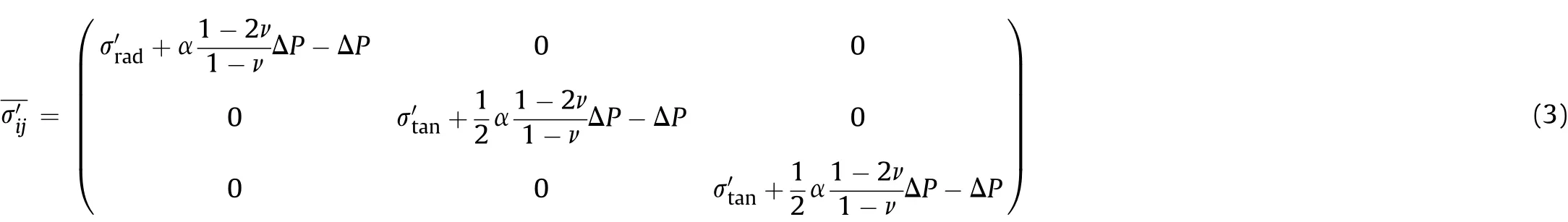
2.2.Maximum sustainable pore pressures for different stress regimes

Based on long-term limits,the maximum sustainable pore pressures,Pc,for fault reactivation is derived with respect to different stress regimes(i.e.extensional,strike-slip and compressional).The Mohr-Coulomb failure criterion for cohesionless fault reactivation is used for the derivation:whereφis the friction angle.This can be rearranged in terms of the

which,whenΔP=Pc-P is introduced and the pore pressure stress coupling(for tangential stresses)is considered,is equal to:

For the following derivations,we introduce a=(1+sinφ)/(1-sinφ)and solve Eq.(6)for Pcfor various stress regimes.Due to the nature of pore pressure-stress coupling,Pcis derived for different locations in the principal axis coordinate system(Fig.1).In order to discuss implications for failure,corresponding differential

Solving this equation for Pcresults in:

The resulting differential stress,σd=σ′1-σ′3,is given by

(2)Alongσ2direction:according to Fig.1 and Eq.(4),bothσ1andσ3represent tangential principal stresses.The Mohr-Coulomb criterion includingΔP=Pc-P becomes:

Solving this equation for Pcresults in:

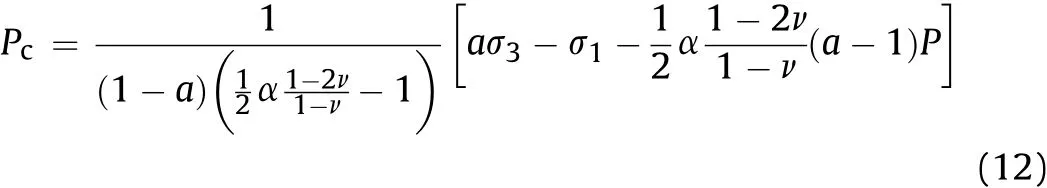
The resulting differential stress,σd=σ′1-σ′3,is given by

(3)Along σ1direction:according to Fig.1 and Eq.(4),σ1then represents the radial principal stress andσ3the tangential principal stress.The Mohr-Coulomb criterion including ΔP=Pc-P becomes:

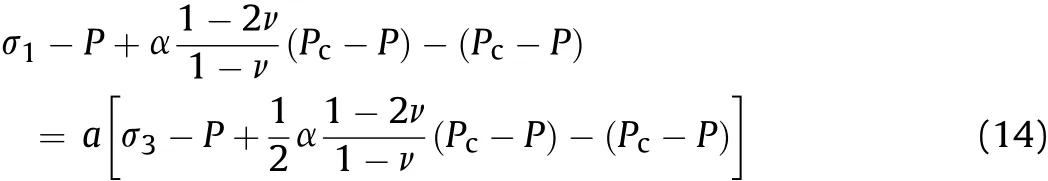
Solving this equation for Pcresults in:

The resulting differential stress,σd=σ′1-σ′

3,is given by

3.Modeling approach

The numerical modeling analysis comprises a finite element analysis based on the prevailing far- field stress regime that is used for a pre-injection assessment of critical sustainable pore pressure differences for different stress regimes and interbedding friction coefficients.It is important to note that the modeling approach is based on the assumption that the anticline structure is pre-existing and that static displacement boundary conditions can be used to simulate different far- field stress regimes.The modeling approach does not consider the structural development of the anticline over geological time scales.Different geological strain rates and material property distributions result in different states of stress of a fold(e.g.Lemiszki et al.,1994).Since folding in most natural cases involves viscous or visco-elastic deformation processes,it is plausible that the syn-folding stress distribution during viscous or viscoelastic folding processes is likely to be relaxed and elastic postfolding deformation events can superimpose the state of stress.It is clear that the modeling approach presented together with the equations to calculateΔPccan also be applied to more complex strain rate dependent model scenarios.However,such an approach requires additional sensitivity analyses reflecting the temporal evolution of deformation which is beyond the scope of this paper.For the purpose of this paper it is assumed that the anticline geometry is pre-existing and that a static state of stress using displacement boundary conditions is considered sufficient for the study of the model parameters of the anticline and represents a common approach to simulate in situ stress states for geomechanical studies(e.g.Rutqvist et al.,2007;Eckert and Connolly,2007;Buchmann and Connolly,2007;Altmann et al.,2014;Eckert and Liu,2014).

The geometry and boundary conditions for the generic anticline structures used in this study are shown in Fig.2a.The model dimensions are6000m (x-direction)× 1500m (ydirection)×2750 m(z-direction).In order to minimize any boundary effects of the numerical model,the anticline is positioned in the center of the model with 1500 m of horizontally layered material on both sides of the anticline.The model geometry comprises a cap rock layer and an injection layer(Fig.2b)as part of a sandstone and shale sequence in the middle of the model which is covered by an overburden layer and supported beneath by a basement layer.The total thickness of the shale and sandstone sequence is 500 m with each layer having a thickness of 100 m.The interface between each layer is modeled as a frictional contact surface enabling in-plane displacements.Four different friction coefficients of 0.1,0.3,0.5 and 0.8 are tested.The material properties for the different layers are given in Table 1.The pore pressure distribution is hydrostatic.

The finite element analyses are run in two consecutives steps using the commercial finite element software code ABAQUS™.The first step serves to equilibrate the gravitational force over the complete model domain(e.g.Buchmannand Connolly,2007;Smart et al.,2009;Eckert and Liu,2014).In the second step,displacement boundary conditions calculated using the equations of linear poroelasticity(Jaeger et al.,2007)are used to generate the strains simulating the different stress regimes in three dimensions.The respective values of the horizontal stresses for the different stress regimes are all calculated for the top of the injection layer in the horizontally layered section.For all regimes,the vertical stress is given by the integration of overburden density.For the extensional stress regime,it is assumed that the sedimentary layers are tectonically relieved and thus the uniaxial strain assumption to calculate the resulting horizontal stresses applies(Engelder and Fischer,1994):

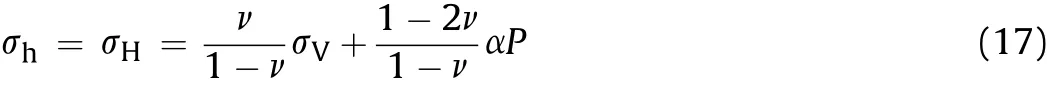
Fig.2.(a)Model geometry and boundary conditions in the x-z coordinate plane.The model extends 1500 m in the y-direction and represents a cylindrical anticline structure.The bottom of the model is constrained in the z-direction,and horizontal strains,εxxand εyy,are used to simulate the stress regimes at the top of the injection layer in the horizontally layered section of the model.(b)Elements of the symmetric cap rock and injection layer sequence for which the results are presented.Locations of“Valley”,“Limb”,and “Crest”denote regions of specific interest.

The strike-slip regime is characterized by σh=0.8σVand σH=1.2σV.The compressional stress regime is characterized by σh=1.25σVand σH=1.5σV.As the state of stress in the cap rock also depends on the magnitude of the Young’s modulus,three different scenarios are tested,i.e.same Young’s modulus for the cap rock and the injection layer,a higher Young’s modulus for the cap rock,and a lower Young’s modulus for the cap rock(Table 1).

Once the stress regimes are established in the horizontal section of the model,it is clear that the geometry of the anticline structure results in a heterogeneous state of stress where the horizontal and vertical stresses are not principal stresses anymore.Based on the far- field stress regimes and the slip occurring between the bedding planes,the principal stress distribution is calculated by the finite element model.The resulting heterogeneous distributions ofσ1and σ3magnitudes for each stress regime are then used to calculate the critical pore pressure,Pc,according to Eq.(15)for various models(with varying friction coefficient and Young’s modulus).

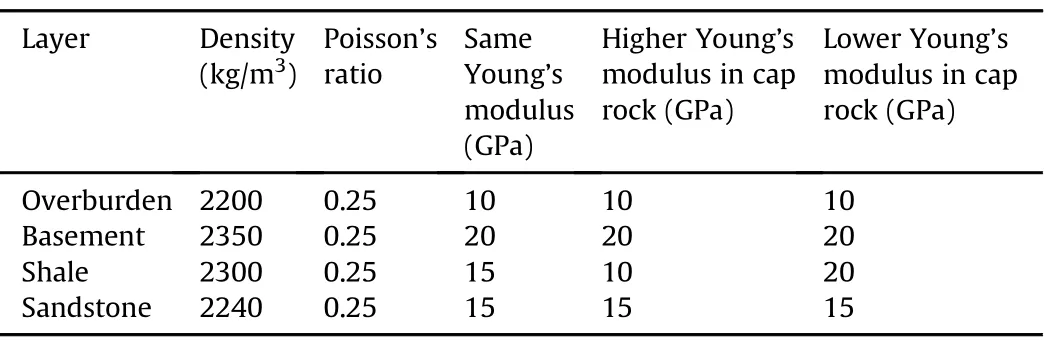
Table 1Model elastic properties for various layers.The injection layer and the cap rock have sandstone and shale properties,respectively.

4.Results

The maximum sustainable pore pressure change,ΔPc=Pc-P,is calculated for each stress regime along the direction posing the largest risk for fault reactivation,i.e.theσ1direction.As the state of stress in an anticline displays variations(Paradeis et al.,2012),it is obvious thatσ1in the anticline limb does not represent an Andersonian stress direction anymore.Assuming a friction coefficient of μ =0.577(i.e.a friction angle ofφ =30°,resulting in a=3)for fault reactivation,α =1,and using the model parameter ofν=0.25 in Eq.(15),the critical pore pressures along theσ1direction for various stress regimes can be determined:

Contour plots ofΔPcfor different model scenarios(i.e.varying Young’s modulus and interbedding friction coefficient,Table 1)for different stress regimes are presented in Figs.3-5,by which plots showing the direction ofσ1(Figs.6-8)are accompanied for better clarification.Only one half of the anticline structure is presented as the results are symmetric.

4.1.Extensional stress regime

The results show thatΔPcvalues range from 0 MPa to 4.6 MPa for various cases tested(Fig.3).In general,it can be observed that lower friction coefficients lead to higher values ofΔPc.For a homogeneous Young’s modulus distribution,lower values ofμ result in slightly lowerΔPcmagnitudes in the cap rock compared to that in the injection layer.If the cap rock features a higher Young’s modulus(E),ΔPcmagnitudes in the cap rockare larger than thosein the injection layer.A lower value of E results in lowerΔPcmagnitudes in the cap rock.In addition,ΔPcvaries along the geometry of the anticline structure.The lowestΔPcmagnitudes occur at the crest,intermediate magnitudes are throughout the limb,and the highest magnitudes are present in the valley of the structure.The most striking observation from Fig.3 is the variation ofΔPcalong the crest of the anticline for all scenarios.At the bottom of the crest ΔPcvalues are 0 MPa,and at the top of the crestΔPcvalues are 1-3 MPa for different values of E andμ.This occurs in both the injection layer and the cap rock.So whilst the top of the injection layer may sustain a modest pore pressure increase,the bottom of the cap rock is subjected to imminent fault reactivation.In contrast,the opposite behavior can be observed at the valley,where the top of the injection layer hasΔPc=0 and the cap rock can sustain magnitudes of 1-4.6 MPa.

4.2.Strike-slip stress regime

The results show thatΔPcvalues range in 4.6-7.7 MPa for various cases tested(Fig.4).In general,lower values ofμresult in higherΔPcmagnitudes.The highestΔPcmagnitudes(～7.7 MPa)occur in the limb of the injection layer for the lowestμ.The lowest ΔPcmagnitudes(～4.6 MPa)occur at the bottom of the crest for the cap rock featuring a higher E than the injection layer and for the lowestμ.In addition,a largerμresults in the largestΔPcat the crest and valley;a lowerμ results in the largestΔPcin the limb.For a homogeneous Young’s modulus(E)distribution,lower values of μ result in slightly lowerΔPcmagnitudes in the cap rock compared to that in the injection layer.The influence of the Young’s modulus shows a clear dependence on the location within the structure.For the limb,a higher E value in the cap rock increasesΔPccompared to that in the injection layer and a lower E value decreasesΔPc.This observation is occurring for allμranging from 0.3 to 0.8.Forμ=0.1,a stronger mechanical decoupling results in slightly lowerΔPcin the cap rock.At the crest,a higher E in the cap rock results in lower ΔPcmagnitudes(～0-5.5 MPa)at the bottom of the crest.

4.3.Compressional stress regime

The results showΔPcvalues ranging from 0 MPa to 27.3 MPa for the various scenarios tested(Fig.5).In general,the results show that the anticline limb can sustain larger pore pressure changes alongσ1direction than the crest and valley(Fig.5).This behavior is amplified for lower friction coefficients,i.e.resulting in large differences ofΔPcbetween the crest and the limb for the lowestμ of 0.1.For a higher E in the cap rock,ΔPcreaches 0 at the bottom of the cap rock.It should be noted again that thisΔPcis characteristic for the σ1direction,which coincides with σHat the crest(Fig.8),but not theσ3=σVdirection.The differences inΔPcat the crest strongly depend on the magnitude of the Young’s modulus of the respective layer.So whilst for a higher E in the cap rockΔPc=0 MPa,the case of a lower E in the cap rock results inΔPc=12-15 MPa.These differences inΔPcwith respect to the location in the anticline structure become less pronounced.The stronger the coupling between the layers(i.e.the higher μ)is,the lower the Young’s modulus for the cap rock becomes,i.e.the case forμ=0.8 and a lower E in the cap rock results in almost uniformΔPcmagnitudes across the structure of～15-18 MPa.

5.Discussion

Calculating the maximum sustainable pore pressure change,ΔPc,prior to fluid injection represents a valuable method to estimate the risk for reactivation of optimally oriented fractures.Previous studies by Rutqvist et al.(2007,2008)concluded that if simplified analytical solutions,which are based on the coupling of pore pressure and the minimum horizontal stress only,are utilized,the poro-elastic effects are difficult to be estimated and hence large discrepancies resulting in overestimation or underestimation ofΔPcarise.The more advanced tensor based concept of pore pressure-stress coupling(Altmann et al.,2010,2014)enables to account for the poro-elastic effects more reliably and,as shown by Eq.(17),analytical solutions can be derived to calculate ΔPcalong the respective direction posing the highest risk for reactivation of optimally oriented fractures for different stress regimes.Such analyses become especially relevant when structural trap systems such as anticlines which feature a heterogeneous state of stress(Paradeis et al.,2012)are considered for fluid injection purposes.If anticline structures are characterized by flexural slip folding and the bedding interfaces are characterized by frictional surfaces,the resulting stress heterogeneities between injection layer and cap rock are amplified.The state of stress at any point in such anticline structures can be simulated using finite element analysis,andΔPccan be calculated for the direction featuring the highest risk of fault reactivation.It should be noted that the absolute magnitudes ofΔPcpresented in this study are strongly subjective and in fact reflect the specific boundary conditions of the generic model setups.The intent of this study is to document the relative importance of various geological parameters considered(i.e.stress regime,Young’s modulus contrasts between injection layer and cap rock,and interbedding friction coefficient).

In the following sections each stress regime is discussed separately,compared to the results obtained from a horizontally layered model featuring the same stress regime,and suggestions for preferred injection locations/conditions are presented.It should be noted that the horizontally layered model for comparison does not include interbedding frictional surfaces as no bending strains need to be accommodated by flexural slip.

Fig.3.ΔPcresults for the various model combinations for the extensional stress regime.Magnitudes range from 0 MPa to 4.6 MPa indicating imminent risk of fault reactivation(gray contours)at the bottom of the crest in the cap rock.

5.1.Extensional stress regime

For the extensional stress regime of the anticline structure modeled in this study,ΔPcmagnitudes range from 0 MPa to 4.6 MPa.The highest risk of fault reactivation occurs in the vertical direction along the crest of the anticline.ΔPcvalues at the bottom of the cap rock are 0 MPa,indicating imminent risk of reactivation of pre-existing normal faults with a dip of～60°.The upper part of the cap rock remains intact.It should also be noted that these shear fractures to occur at the bottom of a fold crest are extremely unlikely and that pre-existing fractures in this location would most likely represent thrust faults with a dip of 30°(Price and Cosgrove,1990;Bergbauer and Pollard,2004).Considering this scenario,ΔPcvalues are most likely larger than 0 MPa(5.5 MPa,if Eq.(17)is adjusted to consider 30°dipping thrust faults),providing a safe,although small,pore pressure difference for injection of fluids.The spatial distribution ofΔPcsuggests injecting fluids at the valley of an anticline structure that is characterized by a higher E in the cap rock and that preferably features a low interbedding friction coefficient.

The overall smallΔPcmagnitudes throughout the anticline structure merit special consideration,especially when compared to horizontally layered bedding planes featuring the same stress regime and geological parameters(i.e.Poisson’s ratio,Young’s modulus,density,uniaxial strain,boundary conditions)as considered in the anticline model.For such conditions,the state of stress is in exact frictional equilibrium(Fig.9a).Visualizing the effects of pore pressure-stress coupling due to fluid injection in a Mohrcircle(following Eqs.(9),(12)and(15);Fig.9b)shows that,along theσVand σHdirections,ΔPcis zero and the risk of fluid injection related fault reactivation is imminent for all layers.Only an increase ofσhby a tectonic contribution(Fig.9c)or a Poisson’s ratio larger than 0.25(Fig.9d)results in a lower risk of fault reactivation and in conditions suitable for fluid injection.The state of stress within an anticline structure represents such a condition and the simulations presented here and the results presented by Amirlatifi et al.(2012)show that fluids can be safely injected into an anticline structure over an extended period of time under an extensional stress regime.

Fig.4.ΔPcresults for the various model combinations for the strike-slip stress regime.Magnitudes range from 4.6 MPa to 7.7 MPa.

Considering this comparison,the question arises if fluids should be injected into horizontally layered media in extensional stress regimes?The low level and frequency of seismicity observed in waste water disposal wells(NRC,2012)indicate that in most likelihood optimally oriented normal faults are not present abundantly in the subsurface and that for a more reliable estimate onΔPc,Eqs.(9),(12)and(15)should be adjusted for intact rock failure(see Appendix).This conclusion is plausible as the generation of optimally oriented normal faults requires extensional tectonic boundary conditions(Jackson and White,1989)to decrease σh.For cases of fluid injection in active extensional tectonic regions such as rift zones or crustal thinning regions,care has to be taken and Eqs.(9),(12)and(15)apply.

5.2.Strike-slip stress regime

For the strike-slip stress regime,ΔPcmagnitudes range from 4.6 MPa to 7.7 MPa.Since the highest risk of fault reactivation occurs approximately along the σHdirection(Fig.7),the results clearly indicate that formations featuring a smaller Young’s modulus in the cap rock should be avoided.For such a case(involving allμ considered),the cap rock features lowerΔPcmagnitudes along this direction.Also,a higher Young’s modulus in the cap rock in combination with a very lowμshould be avoided as this condition results in the lowestΔPcat the bottom of the crest in the cap rock.Most favorable injection conditions occur for a higher E in the cap rock and a friction coefficient of 0.5,resulting in an almost homogeneous spatial distribution ofΔPcin the range of 5.7-6.7 MPa in the cap rock,which would suggest to inject buoyant fluids into the limb or valley and “denser” fluids into the crest region.

Fig.10 shows the contour plots of the injection layer and cap rock layer in a horizontally layered sedimentary basin featuring the same model parameters.The results show that the resultingΔPcmagnitudes of 4.9-6.4 MPa are similar,yet slightly smaller,when compared to that of the anticline model.In contrast to the anticline model,a lower E in the cap rock is favorable,providing higherΔPcmagnitudes;and a higher E in the cap rock actually results in the lowestΔPcmagnitudes.The comparison shows that for the strikeslip regime considered,the anticline formation provides better fluid injection conditions than the horizontally layered structure:the trap geometry of anticlines naturally contains fluids and ΔPcmagnitudes are slightly higher.

Fig.5.ΔPcresults for the various model combinations for the compressional stress regime.Magnitudes range from 0 MPa to 27 MPa.Imminent risk of fault reactivation is present for scenarios featuring a higher Young’s modulus in the cap rock and low friction coefficient between the layers.

5.3.Compressional stress regime

For the compressional stress regime,ΔPcmagnitudes range in 0-27 MPa.The results show that the combination of a higher Young’s modulus in the cap rock and a lower interbedding friction coefficient results in larger stress differences between the limb and the crest.As a result,ΔPcmagnitudes in the cap rock limb are as high as 22 MPa and are 0 MPa at the bottom of the crest which would indicate imminent risk of fault reactivation of thrust faults dipping 30°.It needs to be repeated that these ΔPcmagnitudes are only valid along the σ1direction,which coincides with the σHdirection at the crest of the anticline(Fig.8).ΔPcmagnitudes calculated along theσ3= σVdirection(Fig.11)con firm this observation.Based on Eq.(9),ΔPcmagnitudes along theσ3direction are 5 times the value along theσ1direction,and the spatial distributions ofΔPclows and highs are identical.Moreover,these optimally oriented thrust faults are common features below the neutral surface of buckled and folded layers(Price and Cosgrove,1990).Hence,anticline injection sites featuring a higher Young’s modulus of the cap rock and being characterized by a large degree of flexural slip folding should be avoided.If fluids were injected at the crest of the anticline,a scenario featuring a lower E in the cap rock in combination with a lowμwould represent the most suitable condition.This scenario,besides ensuring spatial containment of the fluids,takes advantage of the higherΔPcmagnitudes(～60 MPa)along the σV= σ3direction at the crest near the injection point and the higher ΔPcmagnitudes along the σ1direction in the cap rock limb(～15-18 MPa).

When compared to a model featuring horizontal layers,the same trend inΔPcmagnitudes can be observed(Fig.12).A lower E in the cap rock features the highestΔPcmagnitudes(～16 MPa),and a higher E in the cap rock features the lowestΔPcmagnitudes(～4.3 MPa).However,it should be noted that ΔPcfor the horizontally layered model represents a uniform number and except for the cases of lower friction coefficients(μ =0.1)whereΔPcmagnitudes in the anticline structure are higher.

Fig.6.σ1orientation for the extensional stress regime models.The σ1orientation represents the direction along whichΔPcmagnitudes are calculated for Fig.3.

Fig.7.σ1orientation for the strike-slip stress regime models.The σ1orientation represents the direction along whichΔPcmagnitudes are calculated for Fig.4.

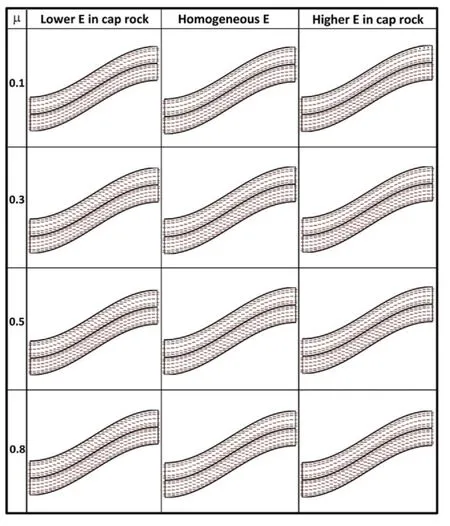
Fig.8.σ1orientation for the compressional stress regime models.The σ1orientation represents the direction along which ΔPcmagnitudes are calculated for Fig.5.

6.Summary and conclusions

The results presented in this study show that the in situ stress regime is a crucial parameter when assessing the risk of fracture reactivation due to fluid injection.This is particular relevant for geological structures with a heterogeneous state of stress such as the generic anticline structures investigated in this study.The results presented show thatΔPcresults are strongly dependent on the relative location with respect to the injection location and are different for each combination of model parameters.

Fig.9.Pore pressure-stress coupling for horizontally layered structures under uniaxial strain conditions.(a)For common Poisson’s ratio of 0.25,the state of stress is in frictional equilibrium and ΔPc=0 MPa.(b)Fluid injection causes imminent risk of fault reactivation along the σvand σHdirections.Only a tectonic contribution to σh(c)or Poisson’s ratio＞ 0.25(d)results in conditions suitable for fluid injection,i.e.ΔPc＞ 0 MPa.

Fig.10.ΔPcresults for a horizontally layered model under a strike-slip regime for the cap rock-injection layer sequence.

In summary,the largest values ofΔPcare obtained for the compressional stress regime and the lowest values ofΔPc(0-4.6 MPa)are obtained for the extensional stress regime,which in general agree with the studies by Rutqvist et al.(2007)and Paradeis et al.(2012).However,these general observations have to be treated carefully,as for special cases(i.e.higher E in cap rock,lowμ)the compressional stress regime may show variations ofΔPcof 0-27 MPa depending on the respective location within the anticline.Whilst the stress regime exhibiting the most homogeneous ΔPcdistribution(4.6-7.7 MPa)without showing any location of imminent reactivation risk(i.e.ΔPc=0)is the strikeslip regime,the most favorable conditions(i.e.a minimumΔPcof～15-18 MPa)are obtained for the compressional regime for anticlines featuring a lower E in the cap rock in combination with a lowμ.

Fig.11.ΔPcresults for various model combinations for the compressional stress regime along the σ3direction.ΔPcmagnitudes are 5 times the values along the σ1direction.

Fig.12.ΔPcresults for a horizontally layered model under a compressional stress regime for the cap rock-injection layer sequence.

For all stress regimes,the differences in the spatial distribution of ΔPcreflect the influence of the Young’s modulus,E,and the interbedding friction coefficient,μ.The general influence ofμ can be summarized as follows:the lower the values ofμare,the higher theΔPcmagnitudes in the anticline limb are;the lower the values ofμare,the lower/higher the magnitudes for the location of the minimum/maximumΔPcat the crest and valley are,respectively.The results presented in this study show that a low interbedding friction coefficient effectively decouples the layers mechanically whilst a larger friction coefficient represents a stronger coupling.This decoupling results in significant stress differences at the crest of the anticline and hence differentΔPcvalues between the top of the injection layer and the bottom of the overlaying cap rock.These differences inΔPchave to be carefully considered as the cap rock is not characterized by a single value forΔPc,contrary to models featuring horizontally layered sedimentary basins.Similarly,for the Young’s modulus,it is observed that a higher E in the cap rock increasesΔPcin the limb but also amplifies the maximum and minimumΔPcvalues in the valley and limb,respectively.These differences inΔPcimposed by E andμare further amplified by different stress regimes.The more compressional the stress regime is,the larger the differences between the maximum and minimum ΔPcbecome.

Besides ensuring spatial containment of the fluids,the comparison to horizontally layered structures shows that,for the majority of parameter combinations,the anticline structure results in higher values ofΔPc(Table 2).This holds true especially for the extensional stress regime,whereΔPc=0 MPa in horizontal layers.For the strike-slip stress regime,the horizontal layer scenario is advantageous when the cap rock features a lower Young’s modulus.For the compressional regime,μsignificantly influences the distribution and magnitude of the minimum/maximumΔPcvalues,respectively.Cases of extremely weak coupling between the layers,i.e.μ=0.1 and a higher E in the cap rock,may result in ΔPc=0 MPa(both in σ1and σ3directions)at the bottom of the crest,and hence should be avoided.For all other coupling scenarios,the location of minimumΔPcis advantageously aligned with theσ3= σVdirection resulting in largerΔPcmagnitudes for this direction.

The numerical modeling results presented in this study clearly demonstrate the complexities that arise when assessing the maximum sustainable pore pressure difference(based on the advanced concept of pore pressure-stress coupling)for realistic structural trap geometries such as anticline structures.In order to make pre-injection analytical estimates ofΔPc,a viable and accurate option,knowledge of the interbedding friction coefficient is of importance.Assuming that Young’s modulus and Poisson’s ratio are known and since there exists no direct in situ measurement of this parameter,accurate stress measurement is an absolute requirement for an appropriate calibration of mechanical numerical models to simulate the pre-injection stress state.This is in agreement with the study of the NRC(2012)which concluded that sufficient data on fault locations,size and fault properties,in situ stresses,and rock properties are necessary to accurately assess seismic risks for fluid injection scenarios on a site-specific basis.

The results based on the simplified analytical derivations(i.e.using long-term limits)show that they are useful to obtain a quick first-order estimate on Pcprior to injection to estimate fault reactivation risk.It is clear that the true nature of pore pressurestress coupling is much more complex(Altmann et al.,2010,2014).In order to include the spatial and short-term temporal relationships,coupled numerical analyses involving all physical processes are necessary.However,as shown by Amirlatifiet al.(2012),the results of the pore pressure evolution with time are strongly dependent on the fluid flow boundary conditions and thus more extensive sensitivity analyses are necessary on a case to case basis.

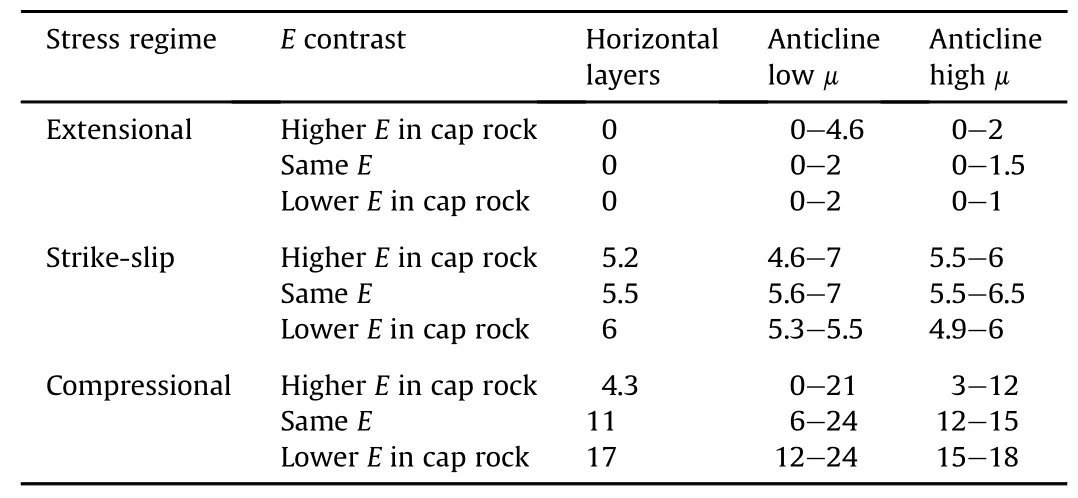
Table 2Comparison ofΔPcmagnitudes between horizontally layered models and anticline models for various stress regimes presented(unit:MPa).

Conflict of interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

The authors gratefully acknowledge the financial support from the US Department of Energy National Energy Technology Laboratory under Grant No.DE-FE0001836.We would like to thank two anonymous reviewers for their valuable and constructive reviews,which greatly improved the manuscript.

Appendix

(1)Intact rock failure equations

In order to calculate the critical pore pressure for the case of intact rock failure,Eq.(5)is adjusted to consider the rock cohesion,So:

Pccan then be obtained for the different principal stress directions.For theσ1direction:

For theσ2direction:

For theσ3direction:

(2)Stress orientations

As Pcis minimal along theσ1direction which does not coincide with the vertical and horizontal directions in an anticline state of stress,σ1directions for various stress regimes are presented(Figs.6-8).

Altmann JB,Müller TM,Müller BIR,Tingay MRP,Heidbach O.Poroelastic contribution to the reservoir stress path.International Journal of Rock Mechanics and Mining Sciences 2010;47(7):1104-13.

Altmann JB,Müller BIR,Müller TM,Heidbach O,Tingay MRP,Weißhardt A.Pore pressure stress coupling in 3D and consequences for reservoir stress states and fault reactivation.Geothermics 2014;52:195-205.

Amirlatifi A,Eckert A,Nygaard R,Bai B,Liu X,Paradeis M.Role of geometrical influences of CO2sequestration in anticlines.In:46th US rock mechanics/geomechanics symposium.American Rock Mechanics Association;2012.p.2277-85.

Barton CA,Zoback MD,Moos D.Fluid flow along potentially active faults in crystalline rock.Geology 1995;23(8):683-6.

Bergbauer S,Pollard DD.A new conceptual fold-fracture model including prefolding joints,based on the Emigrant Gap anticline,Wyoming.Geological Society of America Bulletin 2004;116(3-4):294-307.

Buchmann TJ,Connolly PT.Contemporary kinematics of the Upper Rhine Graben:a 3D finite element approach.Global Planetary Change 2007;58(1-4):287-309.Cappa F.Influence of hydromechanical heterogeneities of fault zones on earthquake ruptures.Geophysical Journal International 2011;185(2):1049-58.

Cappa F,Rutqvist J.Impact of CO2geological sequestration on the nucleation of earthquakes.Geophysical Research Letters2011;38(17).http://dx.doi.org/10.1029/2011GL048487.

Dean RH,Gai X,Stone CM,Minkoff SE.A comparison of techniques for coupling porous flow and geomechanics.SPE Journal 2006;11(1):132-40.

Eckert A,Connolly PT.Stress and fluid- flow interaction for the Coso geothermal field derived from 3D numerical models.GRC Transactions 2007;31:385-90.

Eckert A,Liu X.An improved method for numerically modeling the minimum horizontal stress magnitude in extensional stress regimes.International Journal of Rock Mechanics and Mining Sciences 2014;70:581-92.

Ehlig-Economides C,Economides MJ.Sequestering carbon dioxide in a closed underground volume.Journal of Petroleum Science and Engineering 2010;70:123-30.

Engelder T,Fischer MP.Influence of poroelastic behavior on the magnitude of minimum horizontal stress,Shin overpressured parts of sedimentary basins.Geology 1994;22(10):949-52.

Frohlich C,Potter E,Hayward C,Stump B.Dallas-Fort Worth earthquakes coincident with activity associated with natural gas production.The Leading Edge 2010;29(3):270-5.

Gibbs JF,Healy JH,Raleigh CB,Coakley J.Seismicity in the Rangely,Colorado,area:1962-1970.Bulletin of the Seismological Society of America 1973;63(5):1557-70.

Hillis RR.Coupled changes in pore pressure and stress in oil fields and sedimentary basins.Petroleum Geoscience 2001;7(4):419-25.

Jackson JA,White NJ.Normal faulting in the upper continental crust:observations from regions of active extension.Journal of Structural Geology 1989;11(1/2):15-36.

Jaeger JC,Cook NGW,Zimmerman RW.Fundamentals of rock mechanics.4th ed.John Wiley&Sons;2007.

Lemiszki PJ,Landes JD,Hatcher RD.Controls on hinge-parallel extension fracturing in single-layer tangential-longitudinal strain folds.Journal of Geophysical Research:Solid Earth(1978-2012)1994;99(B11):22027-41.

Li Q,Wu Z,Bai Y,Yin X,Li X.Thermo-hydro-mechanical modeling of CO2sequestration system around fault environment.Pure and Applied Geophysics 2006;163:2585-93.

Metz B,Davidson O,de Coninck H,Loos M,Meyer L.Carbon dioxide capture and storage.Cambridge University Press;2005.

Minkoff SE,Stone CM,Bryant S,Peszynska M,Wheeler MF.Coupled fluid flow and geomechanical deformation modeling.Journal of Petroleum Science and Engineering 2003;38(1-2):37-56.

National Research Council(NRC):Committee on Induced Seismicity Potential in Energy Technologies,Committee on Earth Resources,Committee on Geological and Geotechnical Engineering,Committee on Seismology and Geodynamics,Board on Earth and Sciences and Resources,Division on Earth and Life Studies,National Research Council.Induced seismicity potential in energy technologies.Washington,D.C.:National Academies Press;2012.

Paradeis M,Eckert A,Liu X.Influences of anticline reservoir geometry on critical pore pressure associated with CO2sequestration.In:The 46th US rock mechanics/geomechanics symposium.American Rock Mechanics Association;2012.p.1115-23.

Price NJ,Cosgrove JW.Analysis of geological structures.Cambridge,UK:Cambridge University Press;1990.

Rudnicki JW.Fluid mass sources and point forces in linear elastic diffusive solids.Mechanics of Materials 1986;5(4):383-93.

Rutqvist J,Birkholzer J,Cappa F,Tsang CF.Estimating maximum sustainable injection pressure during geological sequestration of CO2using coupled fluid flow and geomechanical fault-slip analysis.Energy Conversion and Management 2007;48(6):1798-807.

Rutqvist J,Birkholzer J,Tsang CF.Coupled reservoir-geomechanical analysis of the potential for tensile and shear failure associated with CO2injection in multilayered reservoir-caprock systems.International Journal of Rock Mechanics and Mining Sciences 2008;45(2):132-43.

Sanz PF,Pollard DD,Allwardt PF,Borja RI.Mechanical models of fracture reactivation and slip on bedding surfaces during folding of the asymmetric anticline at Sheep Mountain,Wyoming.Journal of Structural Geology 2008;30:1177-91.Settari A,Mourits FM.A coupled reservoir and geomechanical simulation system.SPE Journal 1998;3(3):219-26.

Sibson RH.Brittle-failure controls on maximum sustainable overpressure in different tectonic regimes.AAPG Bulletin 2003;87(6):901-8.

Smart KJ,Ferrill DA,Morris AP.Impact of interlayer slip on fracture prediction from geomechanical models of fault-related folds.AAPG Bulletin 2009;93(11):1447-58.

Streit JE,Hillis RR.Estimating fault stability and sustainable fluid pressures for underground storage of CO2in porous rock.Energy 2004;29(9-10):1445-56.Teufel LW,Rhett DW,Farrell H.Effect of reservoir depletion and pore pressure drawdown on in situ stress and deformation in the Ekofisk field,North Sea.In:Rogiers JC,editor.Rock mechanics as a multidisciplinary science:proceedings of the 32nd US symposium on rock mechanics.Rotterdam:A.A.Balkema;1991.p.63-72.

Twiss RJ,Moores EM.Structural geology.2nd ed.New York:W.H.Freeman and Company;2007.

Verdon JP,Kendall JM,White DJ,Angus DA.Linking microseismic event observations with geomechanical models to minimize the risks of storing CO2in geological formations.Earth and Planetary Science Letters 2011;305(1-2):143-52.

Vidal-Gilbert S,Nauroy JF,Brosse E.3D geomechanical modelling for CO2geologic storage in the Dogger carbonates of the Paris Basin.International Journal of Greenhouse Gas Control 2008;3(3):288-99.

Wesson RL,Nicholson C.Earthquake hazard associated with deep well injection.Open-File Report.The US Geological Survey;1987.p.87-331.

Wiprut D,Zoback MD.Fault reactivation and fluid flow along a previously dormant normal fault in the northern North Sea.Geology 2000;28(7):595-8.

Zhou Q,Birkholzer JT,Tsang CF,Rutqvist J.A method for quick assessment of CO2 storage capacity in closed and semi-closed saline formations.International Journal of Greenhouse Gas Control 2008;2(4):626-39.

Zoback MD.Managing the seismic risk posed by wastewater disposal.Earth Magazine 2012;2:38-43.