Dynamic rock tests using split Hopkinson(Kolsky) bar system-A review

Review

Dynamic rock tests using split Hopkinson(Kolsky) bar system-A review

Kaiwen Xia*,Wei Yao

Department of Civil Engineering,University of Toronto,Toronto,M5S1A4,Canada

A R T 1 C L E 1 N F O

Article history:

Received 22 March 2014

Received in revised form

11 June 2014

Accepted 24 June 2014

Available online 26 December 2014

Rock

Dynamic properties of rocks are important in a variety of rock mechanics and rock engineering problems. Due to the transient nature of the loading,dynamic tests of rock materials are very different from and much more challenging than their static counterparts.Dynamic tests are usually conducted using the split Hopkinson bar or Kolsky bar systems,which include both split Hopkinson pressure bar(SHPB)and split Hopkinson tension bar(SHTB)systems.Signifcant progress has been made on the quantifcation of various rock dynamic properties,owing to the advances in the experimental techniques of SHPB system. This review aims to fully describe and critically assess the detailed procedures and principles of techniques for dynamic rock tests using split Hopkinson bars.The history and principles of SHPB are outlined, followed by the key loading techniques that are useful for dynamic rock tests with SHPB(i.e.pulse shaping,momentum-trap and multi-axial loading techniques).Various measurement techniques for rock tests in SHPB(i.e.X-ray micro computed tomography(CT),laser gap gauge(LGG),digital image correlation(DIC),Moiré method,caustics method,photoelastic coating method,dynamic infrared thermography)are then discussed.As the main objective of the review,various dynamic measurement techniques for rocks using SHPB are described,including dynamic rock strength measurements(i.e. dynamic compression,tension,bending and shear tests),dynamic fracture measurements(i.e.dynamic imitation and propagation fracture toughness,dynamic fracture energy and fracture velocity),and dynamic techniques for studying the infuences of temperature and pore water.

©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

1.Introduction

The accurate determination of rock dynamic properties has always been a very important issue for a variety of rock engineering and geophysical applications,including rock quarrying,rock drilling,rockbursts,blasts,earthquakes,and projectile penetrations.In these applications,rock materials are subjected to dynamic loading over a wide range of loading rates.Therefore,accurate determination of dynamic strength and fracture properties of rocks over a wide range of loading rates is crucial.However,in sharp contrast to many static rock testing methods suggested by the International Society for Rock Mechanics(ISRM),only three dynamic testing methods have recently been suggested by the ISRM Commission on Rock Dynamics(Zhou et al.,2012),including dynamic compression, dynamic Brazil test,and dynamic notched semi-circular bend (NSCB)test using split Hopkinson pressure bar(SHPB),while other methods are good candidates for future ISRM suggested methods.

SHPB system is an ideal and reliable high strain rate loading technique to measure dynamic properties of rocks under high strain rates(102-103s-1).As a widely used device to quantify the dynamic compressive responseof various metallic materials at high loading or strain rates,SHPB was invented by Kolsky in 1949 (Kolsky,1949,1953).Shortly after,researchers started to use SHPB to test brittle materials such as concretes(Ross et al.,1989,1995), ceramics(Chen and Ravichandran,1996,2000),and rocks (Christensen et al.,1972;Dai et al.,2010a).However,some major limitations of using SHPB for brittle materials were not fully explored until two decades ago(Subhash et al.,2000).

Several comprehensive reviews have been conducted concerning dynamic behaviors of brittle materials,such as mortar,ceramic, concrete and rocks(Bischoff and Perry,1991;Malvar and Ross, 1998;Zhao et al.,1999;Toutlemonde and Gary,2009;Walley, 2010;Zhao,2011)and dynamic experimental techniques(ASM, 2000;Field et al.,2004;Ramesh,2008).There are also reviews on rock dynamics and applications(Barla and Zhao,2010;Zhao et al., 2012)and dynamic experimental techniques and results(Xia,2012; Zhao et al.,2012;Zhang and Zhao,2014).The systematic discussion of dynamic experimental techniques for rocks using SHPB system isnot yet available.Therefore the objective of this work is to provide detailed procedures and principles of techniques for dynamic rock tests using SHPB.

This review is organized as follows.After the Introduction, Section 2 briefy describes the history and principles of SHPB system.Section 3 presents new loading techniques for dynamic rock tests and Section 4 discusses the advanced measurement techniques deployed in SHPB for testing rock materials.In Section 5,the dynamic strength measurements for rocks using SHPB system are frst critically assessed,including dynamic compression,tension, bending and shear tests.Dynamic fracture tests are then presented, followed by dynamic techniques concerning the infuences of temperature and water saturation level.Section 6 summarizes the entire paper.

2.History and principles of SHPB system

2.1.History of SHPB system

The name of SHPB was derived from John Hopkinson(1849-1898)and his son Bertram Hopkinson(1874-1918).John Hopkinson investigated the propagation of stress waves in the iron wire in 1872,and his son,Bertram Hopkinson,invented a pressure bar to obtain the pressure-time curve with the dynamic load exerted by detonation(Hopkinson,1914).However,the measurements were not accurate because of the limitation of the measurement technique.Davies(1948)improved the measurement technique by utilizing an electrical method.Later,Kolsky(1949)developed the split bar system,which included two bars(known as incident bar and transmittedbar)with a specimen in between.That is why SHPB is also called the Kolsky bar.Using his SHPB system,Kolsky obtained the dynamic relationship between stress and strain for several materials with condenser microphones.Shortly after that, Krafft et al.(1954)adopted strain gauge to measure the stress waves and applied a striker bar to produce a repeatable impact stress wave in the incident bar.In order to measure valid dynamic properties of different materials,Lindholm(1964)combined previous modifcations and designed an updated version of Kolsky bar system,which became a template of current SHPB system.Thereafter,the SHPB system has been continually improved to obtain more accurate measurements for different materials under high strain rate loading.

In addition to the compression version of Kolsky bar system-SHPB,the tensile version of Kolsky bar system-split Hopkinson tension bar(SHTB)was also developed to obtain the characteristics of materials under dynamic tensile loading.The initial design of dynamic tension apparatus was a hollow tube inside which a single elastic bar and a specimen were attached (Harding et al.,1960).This design was later replaced by placing the entire bar system inside a tube(Hauser,1966;Harding and Welsh, 1983).Meanwhile,the methods using the compression bar system to achieve tensile experiments were also proposed,such as the tophat specimen(Lindholm and Yeakley,1968),and a specimen with a rigid collar(Nicholas,1981).Moreover,other direct tension loading methods for SHTB were also developed:store elastic energy to stretch a section of incident bar in tension(Staab and Gilat,1991; Cadoni et al.,2009),an explosive loading device(Albertini and Montagnani,1974),a ballistic apparatus(Goldsmith et al.,1976),a rotating disk(Kawata et al.,1979;Li et al.,1993),a tubular striker (Ogawa,1984)to impact the fange attached to the incident bar.The design of a tubular striker in SHTB was followed by many researchers(Ross,1989;Li et al.,1993;Chen et al.,2002;Nie et al., 2009;Huang et al.,2010a)and became the standard design of modern SHTB system.The detailed SHTB confguration and procedure are discussed in Section 5.2.1.

The details of the Kolsky bar history,recent modifcation and application have been discussed in ASM handbook(Gray,2000),in the recent book(Chen and Song,2010),and in recent reviews (Nemat-Nasser,2000;Field et al.,2004;Gama et al.,2004;Jiang and Vecchio,2009;Ramesh,2008;Zhang and Zhao,2014).We will discuss the techniques and methods using SHPB for testing rocks in this work.

2.2.Principles of SHPB system

SHPB consists of three bars:a striker bar,an incident bar,and a transmitted bar(Gray and Blumenthal,2000).The impact of the striker bar on the free end of the incident bar induces a longitudinal compressive wave propagating in both directions.The leftpropagating wave is fully released at the free end of the striker bar and forms the trailing edge of the incident compressive pulse εi(Fig.1).Thus,the duration of εidepends on the length and longitudinal wave velocity in the striker.Upon reaching the bar-specimen interface,partof the incident wave is refected as the refected wave εrand the remainder passes through the specimen to the transmitted bar as the transmitted wave εt.Strain gauges are used to record the stress wave pulse on both incident bar and transmitted bar.The principles of the SHTB are similar to those of the SHPB,except that the way to generate the loading pulse and the way to grip the specimen are different as will be discussed later.

In most of the tests,the distance between the strain gauges and the sample should be known,which is needed to determine the starting point of incident,refected and transmitted pluses.Besides, the velocity of the striker bar can be measured by simple optical methods and the strain signals are usually collected using the Wheatstone bridge circuit with amplifcation.

The diameter of bar is governed by the diameter of rock specimen,which should be at least 10 times the average grain size of the rock(Dai et al.,2010b;Zhou et al.,2012).Based on the onedimensional(1D)stress wave theory,the dynamic forces(see Fig.1)on the incident end(P1)and the transmitted end(P2)of the specimen are(Kolsky,1949,1953):

where E is the Young’s modulus;A is the cross-sectional area;εiand εrare the incident strain signal and refected strain signal, respectively.

The velocities at the incident bar end(v1)and the transmitted bar end(v2)are:

where c is the 1D longitudinal stress wave velocity of the bar.

The displacement of the incident bar end(u1)and the transmitted bar end(u2)are thus:

where t is the time.

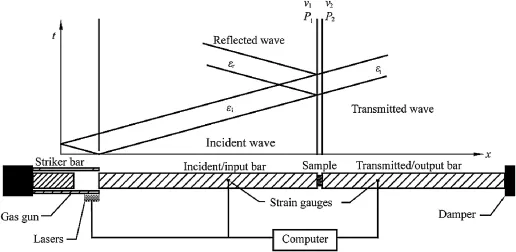
Fig.1.Schematics of a split Hopkinson pressure bar(SHPB)system and the x-t diagram of stress waves propagation in SHPB(after Xia et al.,2011).

One of the objectives of an SHPB test is to determine the material dynamic stress-strain curve,from which the mechanical properties can be derived,e.g.dynamic failure strength,dynamic failure strain and dynamic Young’s modulus.Thus,several methods have been proposed to determine the dynamic stress-strain curve, i.e.one-wave analysis(Gray,2000;Mohr et al.,2010),two-wave analysis(Gray,2000;Gray and Blumenthal,2000),three-wave analysis(Gray,2000;Mohr et al.,2010),direct estimate(Mohr et al.,2010),foot-shifting method(Mohr et al.,2010),hybrid analysis(Perkins et al.,1970;Shan et al.,2000;Gilat et al.,2009),and inverse analysis(Zhao and Gary,1996;Peirs et al.,2011;Pierron and Forquin,2012).These methods have been widely used to calculate stress-strain curves.However,among these methods,one-wave analysis method is very popular because of the simplicity of the formula.The direct estimation method is recommended because it could provide the most accurate stress-strain curves(Mohr et al., 2010).The methods for determining the stress and strain histories in SHPB are critically reviewed(Gama et al.,2004;Zhang and Zhao,2014).To ensure the accuracy of the measurement results with the simple one-wave analysis,one has to guarantee valid testing conditions with some testing techniques,e.g.stress equilibrium for sample,failure sequencesof sample,slenderness ratio of sample,proper lubrication for minimizing the friction effect(Dai et al.,2010b;Zhou et al.,2012).

3.Loading techniques in SHPB system for testing rocks

3.1.The pulse shaping technique

Unlike ductile metals,brittle materials have small failure strains (＜1%)and hence if the loading is too fast as in a conventional SHPB test,the specimen may fail in a non-uniform manner(i.e.the front of the sample may be shattered while the back remains intact).The loading pulse in the conventional SHPB system has an approximately trapezoidal shape accompanied by high level of oscillations. The oscillations induced by the sharp rising portion of the incident wave results in diffculty in achieving dynamic stress equilibrium state or constant strain rate in the sample.However,the stress equilibrium is a prerequisite for valid SHPB tests and the constant strain rate mainly depends on the rise of the incident wave. Moreover,the steep rise of the incident pulse can induce premature failure before dynamic stress equilibrium in the rock sample.

As a rule of thumb,it takes the loading stress wave to travel in the specimen 3-4 rounds for the stress to achieve such an equilibrium state.To achieve accurate measurements in SHPB tests,the dynamic loading has to be slow enough so that the specimen is experiencing an essentially quasi-static load,and thus the deformation of the specimen is uniform.

Frantz et al.(1984)discussed the incident pulse shaping for SHPB experiments of metal samples.Theyemphasized that a slowly rising incident pulse is a preferred loading pulse in order to minimize the effects of dispersion and inertia,and thus facilitate dynamic stress equilibrium of the sample.They also presented experimental results to show a properly shaped loading pulse cannot only provide stress equilibrium in the sample,but also generate a nearly constant strain rate in the sample.Gray and Blumenthal(2000)also discussed these issues in their review paper.Due to larger diameter of rock specimen,longer time is required to facilitate dynamic stress equilibrium of the sample,i.e. the equilibrium time should be 3-10 times of the transit time,the time for stress wave to transverse the sample once(Davies and Hunter,1963;Lindholm,1971;Ravichandran and Subhash,1994).

To change the shape of the incident pulse and to slow down its rising,one way is to modify the geometry of the striker.For example,Christensen et al.(1972)used striker bars with a truncated-cone on the impact end in an attempt to produce ramp pulses.Frantz et al.(1984)used a striker bar with a large radius on the impact face to generate a slowly rising incident pulse for the tests.Li et al.(2000)and Zhou et al.(2012)used tapered or coneshaped striker to generate an approximate half-sine loading waveform,which can achieve the dynamic stress equilibrium and constant strain rate in the rock sample.Another approach for shaping pulse is to place a pulse shaper rod(Gerlach et al.,2011)or an extra specimen between the striker and the incident bars (Ellwood et al.,1982).

The third way for shaping pulse,maybe a more convenient way, is to place a small thin disc made of soft materials between the striker and the incident bars.The disc is called the pulse shaper and can be made of paper,aluminum,brass or stainless steel,with 0.1-2.0 mm in thickness.During tests,the striker impacts on the pulse shaper before the incident bar,thus generating a non-dispersive ramp pulse propagating into the incident bar.This incident pulse with slow-rising front facilitates the dynamic force balance across the specimen(Frew et al.,2001,2002).The function of the pulse shaper is to(i)guarantee constant strain rate during the loading and(ii)maintain force equilibrium across the sample.A wide variety of incident pulses can be produced by varying the geometry of the pulse shaper(Fig.2).Depending on the materials under investigation,different loading pulses are needed and can be achieved with proper shaper design.

The pulse shaping technique is especially useful for investigating dynamic response of brittle materials such as rocks(Frew et al.,2001,2002).Without proper pulse shaping,a large fuctuation of dynamic force occurs on the incident side and a sizeable distinction exists between forces on the two ends of the specimen, thus,it is diffcult to achieve dynamic stress equilibrium in such materials because the sample may fail immediately from its end in contact with the incident bar upon the arrival of the incident wave.With a proper pulse shaper(e.g.copper),the incident wave is modifed from a rectangular shape to a ramped shape.In addition,a small rubber disc is placed in front of the copper shaper to further reduce the slope of rising portion of the pulse to a desired value.In this case,the forces on the two ends of the specimen do not have fuctuation and are almost identical before the maximum value is reached.Thus,the balance of dynamic forces on both ends of the sample can be achieved.

Fig.2.Different loading pulses produced by pulse shaping with shaper(after Xia, 2012).

3.2.Momentum-trap technique

Fig.3a is the photograph of the momentum-trap system for SHPB,which is composed of a momentum transfer fange that is attached to the impact end of the input bar and a rigid mass that is attached to the supporting I-beam for the bar system.

Denoting the length of the incident bar by l,it takes t0=2l/c for the refected wave to arrive at the impact end of the incident bar. The refection wave is then refected and changes from the tensile wave to compression wave at the input end.As a result,it will exert dynamic compression to the sample for a second time.In this way, the sample in a conventional SHPB will thus experience multiple compressive loading.This kind of multi-loading complicates the post-mortem examination of tested samples(Nemat-Nasser et al., 1991).A momentum-trap system similar to that proposed by Song and Chen(2004)is adopted here.The main idea of this method is to absorb the frst refection by a big mass that can be considered as rigid because of its large impedance(which is equal toρcA,whereρis the density)as compared with the bar.

As shown in Fig.3b,there is a gap between the fange and the rigid mass.The distance of the gap,d,is determined by the velocity of the striker,v0,the length of the input bar,l,and the shape of the input pulse.It is required that when the refection wave arrives at the front end of the incident bar,the fange is in contactwith the big mass.As a result,the refected compressive wavewill be changed to tension due to the interaction between the incident bar and the big mass through the fange.This requirement is expressed as

If there is no pulse shaper between the striker and the input bar, the particle velocity of the input bar after impact is 0.5v0for the case where the striker and input bar are made of the same material. Denoting the length of the striker by ls,the total duration of the loading pulse is t1=2ls/c,which is usually much smaller than t0=2l/c.The total displacement of the end of the incident bar (fange),which is equal to the gap between the fange and the rigid mass that we need to set is then

Fig.3.The momentum-trap system:(a)photograph and(b)x-tdiagram showing its working principle(after Xia et al.,2008).

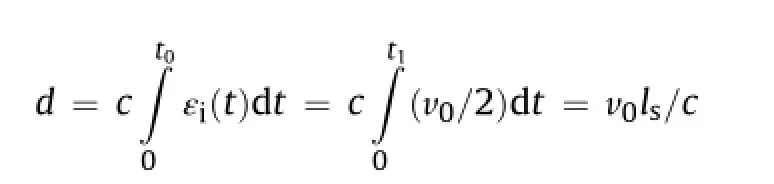
If there is a pulse shaper between the striker and the incident bar,we should use the measured incident pulse to determine the size of the gap using Eq.(4).

As an example shown in Fig.4,the second compression is indeed reduced substantially by the momentum-trap so that the sample will experience essentially a single pulse loading.The second loading pulse is composed of a low amplitude compressive portion followed by a tensile portion.The tensile portion of the pulse will separate the incident bar from the sample,resulting in soft-recovery of the sample for valid post-mortem examination.It is noted that in this test only incident bar is used and thus the incident wave is 100%refected when there is no trap.

The momentum-trap can also be used in SHTB system.Nemat-Nasser et al.(1991)proposed a momentum-trap bar to get the single tension loading and Huang et al.(2010a)further developed this method,as shown in Fig.5.

Fig.4.Comparison of stress waves from the incident bar with and without momentum-trap(after Xia et al.,2011).

The tensile pulse is refected as a compression pulse at the interface between the incident bar and the specimen.If there is no momentum-trap with appropriate gap between the momentumtrap and the fange,the compression pulse will be refected as a secondary tensile pulse,propagating backand pulling the specimen again.The absorption bar 1 is placed next to the fange on the incident bar with a gap.The gap,which can also be calculated byEq. (4),should be accurately set to guarantee that the absorption bar 1 is in contact with the fange when the frst tensile pulse propagates into the incident bar through the fange.The compression pulse transmits into the absorption bar 1 and is trapped because the interface between the absorption bar 1 and the fange cannot support tension.

Moreover,to avoid the refection in the transmitted bar,a back absorption technique is developed,in which the absorption bar 2 is attached to the back end of the transmitted bar using a special joint (Fig.5).The absorption bar 2 has a fange attached to its front end. Before test,the absorption bar 2 is separated from the transmitted bar so that this joint is able to sustain tensile load.When the tensile load is refected at the back end of the absorption bar,it becomes compressive.The joint cannot sustain compressive load and thus the refected wave is trapped in the absorption bar 2.

Fig.6a compares incident wave with and without front absorption bar.The second wave in the incident bar is reduced by 90% with the front absorption design.Fig.6b shows that the refection wave in the transmitted bar is signifcantly reduced by the back absorption method.The specimen is thus subjected to one tensile loading due to the combined momentum-trap method in SHTB.

3.3.Multi-axial loading techniques

There are two types of approaches to achieve multi-axial loading on specimen in SHPB,including true triaxial loading and multi-axial confning loading.For the former,Cadoni and Albertini (2011)designed the true triaxial loading apparatus.However,it is diffcult to carry out synchronized multi-axial dynamic loading during very short dynamic loading time.

The multi-axial confning loading can be classifed as axial confnement,lateral confnement and triaxial confnement,which are highly relevant to underground rock engineering problems.As shown in Fig.7,the rock mass around an underground opening can be divided into three zones depending on the distance to the opening.The confning stress states vary from the dominantlyhydrostatic state in the far zone,to the triaxial state in the intermediate zone,and to the tensile state in the near zone.To effectively consider the dynamic responses of underground rocks,it is thus desirable to submit rock samples to all of these three stress states before the dynamic loading.

Fig.5.Momentum-trap technique in SHTB system(reproduced from Huang et al.,2010a).

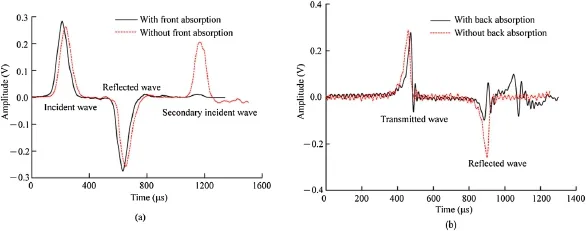
Fig.6.Comparison of(a)the waves in the incident bar with and without front absorption bar and(b)the waves in the transmitted bar with and without back absorption bar(after Huang et al.,2010a).

Fig.7.Zoning of the confning stress states around an underground opening.

In tradition the confned SHPB tests for brittle solids,usually lateral confnements were used,which were achieved by a hydraulic pressure chamber(Christensen et al.,1972;Malvern et al., 1991;Gary and Bailly,1998)or a passive thick confning vessel (Gong and Malvern,1990;Rome et al.,2004;Forquin et al.,2008, 2010).For fne-grained brittle solids like ceramics,other types of confnements were possible,such as a shrink-ft metal sleeve(Chen and Ravichandran,1996,1997;Yuan et al.,2011)and planar confnement(Paliwal et al.,2008).

Lindholm et al.(1974)conducted the pioneer work in the dynamic tests of rocks under hydrostatic confnement and proposed a system to determine the dynamic properties of rocks under triaxial confnement.It is composed of an SHPB system with two hydraulic cylinders and the sample is enclosed in the lateral confning cylinder.The lateral confning cylinder exerts confning stresses in the transverse direction and the axial confning cylinder applies the axial confning stress.Their original design was only recently improved by other researchers(Li et al.,2008;Frew et al.,2010).In their experimental design,Li et al.(2008)connected the two pressure cylinders with two tie-rods.Although they claimed that they can do triaxial confnement,they only showed results on axial confnement in their work.Using a very similar idea,Frew et al. (2010)designed a system that can apply hydrostatic confnement with four tie-rods to connect the two cylinders(shown in Fig.8). The method to achieve such a confning state is to frst expose the cylindrical rock sample to the confning fuid and then to maintain the same fuid pressure in both cylinders.They reported dynamic compressive responsesofIndiana limestone athydrostatic confning pressures up to 200 MPa and strain rates of 400 s-1.

3.4.Strain controlling technique

The ideal way to study the dynamic damage evolution in the brittle materials would be to use the real-time three-dimensional (3D)scanning,which has been applied in quasi-static studies (Raynaud et al.,1989;Kawakata et al.,1999;Feng et al.,2004; Desrues et al.,2006).However,it is very challenging to employ this method in dynamic tests.Thus,strain controlling technique, also known as deformation controlling method,was developed.

The principle of this method is to control the strain of specimen during dynamic tests.Huang et al.(2013)performed the SHPB tests with strain control ring to examine microscopic damage accumulation in brittle solids subjected to dynamic compressive loading. The system consists of a striker bar,an incident bar,a transmitted bar,and a strain control ring(shown in Fig.9).Pulse shaping technique was utilized to achieve dynamic stress equilibrium and to eliminate the inertia effect inside the sample subjected to dynamic loading.The forces on both ends of the specimen can be calculated by Eq.(1)and the history of the stress,strain and strain rate are then calculated(see Section 5.1.3).

A steel ring was mounted on the end of the transmitted bar (Fig.9).Because the impedance of the ring is the same as the bars and much larger than that of the rock,the deformation of sample will be essentiallyceased when its length is equal tothatof the ring. Before this point,the sample frst deforms freely.Thus,the strain of the sample is determined by the gap between the ring and the incident bar.With the different distances of the gap,the strain levels of specimen can be changed.

The stress-strain curves are shown in Fig.10 with the same loading condition.A complete stress-strain curve was achieved from the rock sample without constraining the strain.The stressstrain curves of all samples agree well with the complete stressstrain curve before contact points,where the incident bar hits the strain control ring.The good agreement validates this method of studying damage accumulation.The stress-strain curve after contact points represents the combination of behavior of the sample and the ring.This section of curve is dominated by the behavior of the ring,resulting in a deviation after the contact point in the curve.

4.Measurement techniques in SHPB system for testing rocks

Fig.8.Schematics of confned SHPB system for testing rocks(Frew et al.,2010).

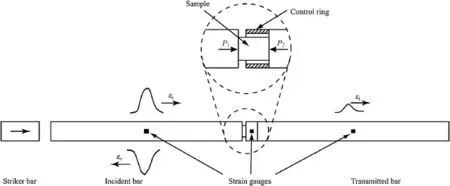
Fig.9.Schematics of the SHPB with the strain control ring(after Huang et al.,2013).

Besides loading techniques in the SHPB system,quantitatively obtaining dynamic properties and strain(deformation)feld is critical for fully understanding the material behavior and failure mechanism.Traditional measurement techniques,such as strain gauges mounted on the bars and mechanical extensometers,provide limited information about dynamic behaviors of rock materials.Several optical measurement techniques were thus developed to capture fracture process and reveal fracture mechanism.The optical measurements for high rate deformation in rock-like materials have been reviewed by Field et al.(2004)and Zhang and Zhao(2014).In this section,the optical measurement techniques for rock materials in the SHPB test are discussed,along with X-ray micro computed tomography(CT)technique as a non-destructive pre-test and post-mortem material examination method for SHPB.

4.1.X-ray micro CT technique

The microscopic observation is critical for studying dynamic damage evolution and dynamic failure of brittle solids.X-ray micro CT can be used to examine the micro-cracks/voids inside the heattreated sample or rocks under static/dynamic loading(Feng et al., 2004;Huang et al.,2013).The CT value(Hounsfeld radiological density)is used to represent the attenuationwhen the X-ray passes through the material,and to indicate the density of materials after scaled with standard materials with the unit of Hu(-1000 Hu for air and 0 Hu for pure water).Thus,the average CT values of samples can be used to describe the damage introduced by the heattreatment or static/dynamic loading.

Fig.10.The stress-strain curves of samples under various strains(after Huang et al., 2013).

Because the damage of sample is usually presented as three dimensions,thetraditionaltwo-dimensional(2D)microscopic observation technique of SEM(Huang et al.,2010b;Yin et al.,2012) usually provides incomplete information and involves sample cutting and polishing(Curran et al.,1987).As a promising unique nondestructive method,X-ray CT technique can provide a 3D microscopic observation to investigate physical properties and failure mechanics of geomaterials(Vinegar,1986;Renter,1989;Vinegar et al.,1991;Van Geet et al.,2000;Mees et al.,2003;Otani and Obara,2004;Viggiani et al.,2004;Matsushima et al.,2006;Yun et al.,2013;Jia et al.,2014).Real-time X-ray scan has been introducedtoobservethefracturemechanismandthedamageevolution for rocks under static loading(Raynaud et al.,1989;Vinegar et al., 1991;Kawakata et al.,1999;Feng et al.,2004;Viggiani et al.,2004; Desrues et al.,2006;Bésuelle et al.,2010;Parab et al.,2014).However,it is diffcult and challenging to achieve this in dynamic tests. Recently,Luo et al.(2012)used X-ray phase contrast imaging(PCI) technique to acquire 2D image of samples under dynamic loading. Hudspethetal.(2013)alsoutilizedX-rayPCImethodtoimagesingle particle sand interaction,fber-epoxy interfacial failure and singlecrystal silicon fragmentation due to dynamic compression and tensile loading.The Kolsky bar systems with synchrotron X-ray PCI technique achieved an image with 500 ns temporal resolution and 2μm spatial resolution,through which the in situ interior of the materialsystemduringhighrateloadingwasanalyzed.Shortlyafter, high-speed synchrotron X-ray PCI technique was utilized to study thedamagemechanismsinsandparticlesunderdynamic compressive loading(Parab et al.,2014)and to monitor the in situ damage history in a dynamically deforming specimen(Chen et al., 2014).Whereas this technique has limited feld of view(2-10 mm)and can only offer a series of 2D results during dynamic loading.An effcient waytoovercome these limitations is torecover the sample at different deformation levels and conduct postmortem examination(Curran et al.,1987).

Huang et al.(2013)employed X-ray micro CT method and strain-control ring in the SHPB tests to observe microscopic damage accumulation in brittle solids subjected to dynamic compressive loading.X-ray micro CT with high resolution was used to examine the 3D microcrack inside the recovered rock sample under various strains.The low density areas are the cracks shown as black lines in Fig.11a;while the high density areas are the mineral grains shown as white and gray.Cracks were recognized and transferred to white pixels,while the remainder is transferred to black pixels in Fig.11b.

Two perpendicular views of the sample are provided in Fig.12, with gray dots representing low density constituents in the sample such as voids and cracks.

Fig.11.Processing of CT images:(a)8-bit gray image;(b)processed crack pattern image(cracks shown as white)(after Huang et al.,2013).

4.2.Laser measurement techniques

Thelasermeasurementtechniquesareusuallyused for measuring the specimen deformation(Li and Ramesh,2007; Ramesh and Narasimhan,1996)or the crack opening displacement(COD)(Tang and Xu,1990;Chen et al.,2009).The principle of laser measurement technique for obtaining the COD is that the luminous fux of laser or light passing through a chink on the specimen is proportional to the electrical signal.When the amount of laser passing through the chink on the specimen increases with the COD,the increasing illuminated energy can be detected by high frequency laser/light detector and thus the variation of COD can be also calculated by the electrical signal recorded.

In the fracture tests conducted by SHPB system,a laser gap gauge(LGG)system was utilized to monitor the opening of the notch and thus to reduce the opening velocity of the cracked fragments(Chen et al.,2009).As shown in Fig.13,the system consists of three major components:the collimated line laser source,the sensing system and the mounting system.LGG is mounted perpendicular tothe bar axis and the laser passes through the notch in the center of the specimen.

Fig.12.3D imagesof microcracks in the rocksample viewed from twoangles.Gray dots represent cracks and the black arrows are the view directions(after Huang et al.,2013).

Before the test,the calibration of LGG system should be conducted under both static and dynamic conditions(Chen et al., 2009).For static calibration,a set of high accurate gauges was used to partly block the probe laser.With the increase of blocking width,a specifc blocking width corresponded to a light-passing widthΔdand a certain amount of voltage readingΔUin the detector.Then,the calibration parameter of the LGG system can be calculated.For the dynamic calibration,while one end of the incident bar was impacted with the striker bar,the LGG was used to monitor the motion of the other free end of the incident bar.The displacement of the free end of incident bar can be obtained from the incident and refected waves measured from the strain gauge glued on the incident bar with the following formula:

During the test,as the notch opens up,the amount of light passing through the specimen increases,leading to a higher voltage output from the detector.The voltage is linearly proportional to the gap width and thus the crack surface displacement can be reduced. The detailed experimental procedures using the LGG system in the SHPB testing are presented in Section 5.4.

Fig.13.Schematics of the LGG system(after Chen et al.,2009).

4.3.Digital image correlation(DIC)

With the progress of advanced image processing methods (Siviour et al.,2011),high-speed calculation and high-speed camera,the DIC technique has become a promising and popular tool for brittle materials in high loading rate tests(Siviour and Grantham, 2009;Sutton et al.,2009;Zhang and Zhao,2013a;Gao et al., 2014).On one hand,this technique can be applied to experiments with a broad feld range from microscale to feld scale.On the other hand,adopting the high-speed camera with the high spatial and temporal resolution,the DIC technique can also be applied to a wide range of loading rates(Zhang and Zhao,2013a).

Asanon-contactandopticalfull-feldmeasurementmethod,the DIC technique is easy to be applied and provides satisfactory resolution of the displacement feld.The DIC method deals with a reference image recorded before deformation and a series of deformed images recorded after deformation.The basic principle of DIC is to track and match the same pixel points located in various deformedimages(asshowninFig.14).Generally,insteadoftracking a single pixel,a square reference subset or subimage (2N+1)×(2N+1)centered at the considered point is chosen and tracked in the deformed images using selected correlation function such as zero-normalized cross-correlation(ZNCC)(Bornert et al., 2009;Pan et al.,2009;Rastogi and Hack,2012;Amiot et al.,2013). The purpose of DIC algorithms is to fnd the displacement of the center of each subimage.By optimizing the correlation coeffcient, the location of a subimage in the deformed image is found and the displacement components of this subset center can be determined. The corresponding point P′(x′,y′)after deformation related to the coordinate P(x,y)in reference image can be calculated as

where u,v are the displacement components of the subset center point O in x,y directions,respectively;Δx andΔy are the distances from point P to point O;and∂u/∂x,∂u/∂y,∂v/∂xand∂v/∂yare the gradients of displacement components for the subset shown in Fig.14.By optimizing the correlation function,the peak position of the distribution of correlation coeffcient can be searched and thus the horizontal displacementuand the vertical displacementvcan be determined.If the same tracking procedure is repeated on the other points of interest,full-feld displacements of the zone of interest(ZOI)are obtained.Then,the full-feld strains can be computed from the full-feld displacement.Finally,other parameters,e.g.stress,fracture toughness,and fracture velocity,can be calculated from the full-feld strains(Hild and Roux,2006;Avril et al.,2008;Pan et al.,2009;Rastogi and Hack,2012;Gao et al., 2014).

The SHPB experimental setup for DIC measurement is shown in Fig.15,which mainly includes a striker,an incident bar,a transmitted bar,an absorption bar and a high-speed camera.The incident wave signal was used to synchronize the high-speed framing camera and the fash light in the tests.The focus of high-speed camera was adjusted manually under focused mode to obtain images with optimal quality.The captured images were processed frst to enhance image qualityand then used for post-analysis using a program to obtain the surface deformation characteristics(e.g. displacement and strain felds,onset of fracture).

With the DIC technique,the SHPB tests were performed to determine dynamic properties of rocks(Zhang and Zhao,2013a, 2013b;Gao et al.,2014).The displacement and strain felds during the whole process were frst determined using DIC method.The location of the crack tip,the fracture initiation toughness,the fracture propagation toughness,the fracture energy,the dynamic tensile strength,and the dynamic uniaxial compressive strength were subsequently calculated using the deformation felds.The DIC method also provides much more information on the fracture propagation process and the reliable full-feld strain felds in the specimens under dynamic loads(Zhang and Zhao,2013a).

4.4.Moiré methods

Moiré techniqueshavebeen introduced to measure the displacement felds of specimens.Dynamic Moiré techniques have also been developed to measure the critical time of dynamic fracture and wave and fracture propagation in rock samples(Daniel and Rowlands,1975;Yu and Zhang,1995;Zhang et al.,1999).

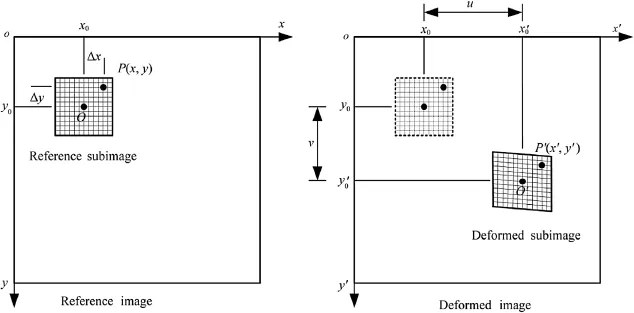
Fig.14.Schematics of reference and deformed subsets(after Gao et al.,2014).

Fig.15.Schematics of the SHPB testing system with high-speed camera(after Gao et al.,2014).

The confguration of dynamic Moiré method is shown in Fig.16. Two optical gratings were mounted to each side of the specimen separated by the main crack plane.The centers of both gratings were installed on the same section of the tip of the pre-machined crack.During dynamic fracture,the COD increases with time.Then, the value of COD can be recorded from the relative movement of the two gratings.Once the crack approaches the critical state,the speed of the crack open displacement(SCOD)reaches an extreme value.This moment is considered to be the critical time of dynamic fracture,which can be determined by the curve of the SCOD with time obtained by experimental results(Yu and Zhang,1995).

The magnitude of signal recorded from the two optical gratings on the specimen changes periodically.According to the operating principles of the optical gratings,one period of the signal represents a constant displacement in which the two gratings move relatively to each other.The total displacement represents the COD. Then the data of the COD with time can be obtained and thus the SCOD with time can be derived from the COD.The values of the critical time of dynamic fracture measured by the dynamic Moiré method can be determined and the corresponding fracture toughness can also be calculated(Zhang et al.,1999).Because the measurements are inferred from the gratings,the inertial effect of the gratings is assumed to be negligible.

4.5.Caustics method

The caustics method has been employed to investigate dynamic fracture of transparent materials(Field et al.,2004;Ravi-Chandar, 2004)and opaque material with refective surface(Yang et al., 2009).The caustics method for transparent materials requires mirror surface fnish of the specimen,which is hard for rocks. Therefore,this caustics system is not applicable for rock materials (Field et al.,2004;Zhang and Zhao,2014).A refective dynamic caustics system is shown in Fig.17.This system is employed with an impact load system,a multi-spark high-speed camera and a light to electric signal transducer.The high-speed camera system contains a 4×4 array point light source,feld lenses,a half-refective mirror, and a 4×4 array camera.The output aperture of the spark gapshould be small enough to generate a point light source for obtaining the caustic spot.The light from each spark is frst refected by the mirror surface of the specimen.It then enters into the camerawhere the caustic images are obtained.A time delaycontrol circuit was applied to synchronize the impact load with the sparks (Yang et al.,2009).

Fig.16.Schematics of the dynamic Moiré technique.(1)Rock specimen;(2)optical gratings;(3)He-Ne laser;(4)optical conductive fber;(5)photo-multiplier;(6)transient recorder;and(7)high-voltage power(after Zhang et al.,1999).

Fig.17.Schematics of experimental optical system for refected caustics.S-light source,F-feld lenses,M-half-refective mirror,L-camera,R-reference plane(after Yang et al., 2009).

With the caustic image,the location of crack tip during crack propagation can be accurately determined.Hence,the crack growth length and the crack growth velocity can be measured at each time instance.Besides,according to the caustic patterns of crack tip propagation in mode I,values of the dynamic stress intensity factor (SIF)can be determined as follows(Yang et al.,2009):

whereDmaxis the maximum transverse diameter of the caustic at the crack tip;ηis a convergence factor for incident light,η=Z1/ (Z1+Z0),Z0is the distance between the specimen plane and the image plane,Z1is the distance from the reference plane to the focus;dis the effective thickness of the specimen;ζis the dynamic optical constant;andF(v)is a velocity correction factor.

It is noted that the caustic method is based on singular term of the dynamic stress feld around a crack.For a fast propagation fracture,more terms are necessary to describe the stress feld and thus error of the caustic method would be signifcant(Xia et al., 2006).

4.6.Photoelastic coating method

The photoelastic coating method extends photoelastic method to measure the surface full-feld stress on opaque materials.The photoelasticcoatingtechniqueconsistsofalightsource,asetofrefection polarizer sheets,birefringent coatings and a camera.This method requires elaborate and well-polished surface of the specimen.Since a thin sheet of photoelastic material is glued directly to the wellpolished surface of materials with a refective cement,the photoelastic coating will deform with the material.Thus,in the coating,the strainfeldwillbeproduced,representingthestrainfeldofmaterials. By employing a set of refection polarizer sheets,the isochromaticfringe patterns can be recorded and thus used to determine the crack propagation and dynamic parameters of rock material.

A qualitative investigation of wave and crack tip propagation in marble specimen has been performed by Daniel and Rowlands (1975).However,the failure of a continuous birefringent coating on specimen may cause error since the coating failure may not represent the fracture of material.To address this problem,a split birefringent coating can be glued on the both sides of the anticipated path of the crack(Zhang and Zhao,2014).

4.7.Dynamic infrared thermography

Using the energy dissipation and temperature variation due to bulk dynamic deformation and fracture,the infrared thermography can transform the thermal energy emitted by specimen in the infrared band spectrum into a visible image.Shi et al.(2007) employed thermal infrared(TIR)imager to monitor the transient process of marble plates impacted by a high-speed striker.By using thermal infrared radiation camera,the thermal infrared radiation energy can easily be measured since there is a distinct variation in temperature due to impact.The results show that there is a critical impact velocity at which target thermography is regular and centrally symmetrical and this method might be extended to analyze the fracture and strain feld for rock materials under dynamic loading.

5.Dynamic testing methods for rocks

5.1.Dynamic compression tests

The compression tests of SHPB are based on two fundamental assumptions:(i)1D elastic wave propagation in the bars and(ii) homogeneous deformation of the sample(Kolsky,1953).The assumption of 1D stress wave propagation is ensured by using long bars,and the elasticity of the bar deformation is guaranteed throughout the test bylimiting the impacting velocityof the striker. The homogeneity of the sample deformation is affected mainly by two factors:inertial effects(i.e.the axial inertial effect and the radial inertial effect)and the interfacial friction effect.

5.1.1.Inertia effects and slenderness ratio

For high strain rate tests,inertial effect becomes more signifcant,which has to be reduced or eliminated to carry out valid and precise dynamic tests.The inertial effect attributes to the apparentstress and the size of the specimens(Field et al.,2004).The ideal slenderness ratio(i.e.the length to diameter ratio)of the sample has long been studied because it plays a major role in the inertial effects during the dynamic SHPB test.Based on the synthetic analysis of both axial and radial inertia effects,Davies and Hunter (1963)suggested an optimal slenderness ratio ofL/D= 3ν/2, whereLis the length of the cylindrical sample,andνis the Poisson’s ratio of the testing material.This suggested slenderness ratio has been frequently used to design the sample geometry for metals (Meng and Li,2003).To limit the inertial effects associated with stress wave loading,the slenderness ratio of samples cannot be too large.When SHPB is frst introduced to the dynamic testing community,the incident wave is in rectangular shape with a sharp rising edge and high oscillation,it is harder to minimize the axial inertial effects because it takes longer time for the sample to reach stress equilibrium.However,with developed pulse shaping technique(Frew et al.,2001,2002),even a relative long compressive sample can easily obtain stress equilibrium,thus reducing the axial inertial effects to a negligible amount.For the radial inertia effect, signifcant progress has been accomplished in experimental tests (Zhang et al.,2009),theoretical investigations(Forrestal et al., 2007)and numerical simulations(Li and Meng,2003;Li et al., 2009;Lu et al.,2010).These studies demonstrate that inertialinduced radial confnement makes a large contribution to the enhancement of compressive strength when the strain rate is greater than the critical transition value,and the radial inertial effect is proportional toD2s,whereDsis the diameter of sample.A review of radial inertial effect on the compression behavior of concrete was presented by Bischoff and Perry(1991).

5.1.2.Friction effect

Friction effect is another major concern in SHPB test.As early as SHPB was frst introduced as a useful dynamic testing tool,it was realized that the interfacial friction on both ends of the sample may affect the testing results(Kolsky,1949,1953).When the sample is loaded by the compressive stress wave in the SHPB test,it expands radially due to the Poisson’s effect.If the sample/bar interfaces are notsuffciently lubricated,the resulting interfacial friction force can be signifcant.This friction force infuences the accuracy of the testingresultsby applyingadynamicconfnementtothe compressive specimen,whose stress state should be uniaxial by assumption.This additional sample stress can yield pseudo rate effects of the material(Scheyet al.,1982),e.g.Shewmon and Zackay (1961)mistakenly concluded that the aluminum alloy was a rate sensitive material because they glued the sample on the bars during their tests.In addition,the sample is no longer deforming uniformly because of this dynamic confnement(Narayanasamy and Pandey,1997),whose effect is the largest on the ends and diminishes toward the center of the specimen.Bell(1966)examined the distribution of stress and strain in the SHPB tests and found that there exists marked discrepancy between the measured strain from SHPB data reduction and the strain directly measured from the sample surface.With the fnite difference method,Bertholf and Karnes(1975)simulated SHPB tests on samples with three types of slenderness ratios and interfacial frictions to investigate both inertial effects and interface friction effects.They drew the same conclusions as Bell(1966)that without enough lubrication at the boundary interfaces,the stress state in the sample is inhomogeneous and big deviation of measurement occurs inevitably. Malinowski and Klepaczko(1986)presented a united analytic and numerical approach to investigate inertia and friction effects in SHPB tests on annealed aluminum with consideration of energy balance.They concluded that proper treatment of frictional effects along with inertia is crucial for the determination of accurate material response during plastic deformation.Some researchers have performed experiments on ring specimens and have suggested that the friction effect can be well reduced(Hartley et al.,2007;Zhang et al.,2009;Alves et al.,2012).Gray(2000)stated that friction can be reduced by minimizing the area mismatch between the specimen and bars(DS≈0.8DB).Meng and Li(2003)revisited the combined effects of slenderness ratio and the interface friction numerically.Lubrication is recommended to minimize the friction effect,but cannot eliminate the friction effect.

To limit the friction effect,the slenderness ratio of a compressive sample should be large enough.This can be manifested from a recommended slenderness ratio of 2 or larger for static compressive tests of rocks by the ISRM(Bieniawski and Bernede,1979).On the other hand,the slenderness ratio should be short enough to limit the inertia effects.Thus,an optimal slenderness ratio is needed to minimize both the inertial effects and the friction effect (Xia,2012).

5.1.3.Dynamic uniaxial compression method

Dynamic compression is the most common test using SHPB.The histories of stressσ(t),strain ε(t)and strain rate˙ε（t）within the sample in the dynamic compression tests(Fig.18)can be derived as (Kolsky,1949):

whereAis the area,andA0is the initial area of the sample. Assuming that the stress equilibrium condition or uniform deformation prevails during dynamic loading(i.e.P1=P2or εi+εr=εt) in Eq.(8),Eq.(8)can be rewritten as

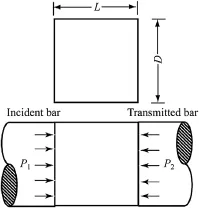
Fig.18.The sample in the compression test using SHPB(after Dai et al.,2010b).

To avoid end effect,the sample with slenderness ratio of 2 or larger is normally used in static compression tests.As discussed above,the slenderness ratio has been a fundamental issue in dynamic compression tests with SHPB because it has a majorinfuence on the axial inertia effects for the tests.Shorter samples facilitate dynamic stress equilibrium and are thus preferred.The higher the slenderness ratio of the sample,the higher the axial inertial effects,and the lower the relative radial inertial effects(also the friction effects).

In conventional SHPB tests,a rectangular incident wave is generated by a direct impact of the striker to the free end of the incident bar.This incident wave features a very sharp rising part with signifcant oscillations.Thus,for standard SHPB method,the recommended slenderness ratio is from 0.5 to 1(Gray,2000). However,for brittle solids like rocks with small failure strain,the sample may fail immediately from its end when it is impacted by the incident bar.Hence,the pulse shaping technique has been widely utilized for SHPB testing on brittle materials such as rocks. With the pulse shaping technique,the striker impacts the pulse shapers right before the incident bar,generating a non-dispersive ramp pulse propagating into the incident bar and thus facilitating the dynamic stress equilibrium in the specimen(Frew et al.,2001, 2002).Under stress equilibrium,the stress gradient vanishes,and inertial effects induced by stress wave propagation are thus minimized.Xia et al.(2008)used the C11000 copperdisc in combination with a small rubber disc together as the shaper to transform the incident wave from a rectangular shape to a ramped shape.Fig.19 shows the dynamic stress in a typical dynamic compression test.It is shown that the time-varying stresses on both sides of the samples match with each other before the peak point is reached during the dynamic loading.The sample is thus in a state of dynamic stress equilibrium.It is also noted that the resulting stress on either side of the sample also features a linear portion before the peak,thus facilitating a constant loading rate via˙σ=k1A/A0.The parameterk1in the equation is illustrated in Fig.19.Since there is no stress gradient in the sample(dynamic stress equilibrium has achieved), the axial inertial effect is thus negligible.

Without the axial inertial effect for brittle materials in SHPB tests,the effect of the slenderness ratio on dynamic compressive strength of rock-like materials has also been studied under the dynamic stress equilibrium(Dai et al.,2010b).As shown in Fig.20, there are no signifcant differences of strengths from samples with selected slenderness ratios.For dynamic compression tests on rocks,it can be concluded that with bar/sample interfaces fully lubricated and thus with axial inertial effects minimized,the slenderness ratio has little infuence on the testing results within the range of 0.5-2.Therefore,the samples with a slenderness ratio of 1 are recommended in dynamic compression tests of rocks for convenience since it is diffcult to hold shorter samples during sample fabrication.In the ISRM suggested methods for rock dynamic compression,both slenderness ratios of 0.5 and 1 are acceptable(Zhou et al.,2012).

Fig.19.Dynamic stresses on both ends of disc specimen tested using a modifed SHPB with careful pulse shaping(after Dai et al.,2010b).In,Re,Tr denote incident,refected and transmitted wave,respectively.

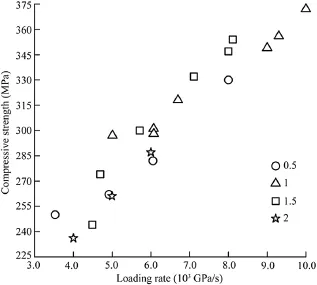
Fig.20.Dynamic compressive strengths with loading rates measured from rock samples with varying slenderness ratio of 0.5,1,1.5 and 2(after Dai et al.,2010b).

To manifest the friction effect on the measured strength,the samples with three different friction boundaries on the bar/sample interfaces for the sample slenderness ratio of 1 were used by Dai et al.(2010b):fully lubricated with vacuum grease,dry and bonded.The bonded bar/sample interface completely restricts the motion of the rock surfaces on the barand is believedtoprovide the maximum dynamic confnement to the sample.Fig.21 illustrates the trend of the rate effects of compressive strength under these three boundary friction conditions with dynamic stress balance on both ends of the sample and a constant loading rate.Samples with bar/samples interfaces fully lubricated yield the lowest measured compressive strength while the samples with bonded interfaces own the highest.Thus,the friction effect in dynamic compressive tests on rocks is signifcant.The measured compressive strength increases with increasing friction involved in the tests.To obtain the actual dynamic compressive response of rocks,the bar/sample interfaces should be suffciently lubricated.

Fig.21.Dynamic compressive strengths with loading rates measured from rock samples(L/D=1)with three interfacial friction boundaries(after Dai et al.,2010b).

With three types of lubricated bar/sample interfaces,the recovered samples from the tests with the data points ofA,BandCin Fig.21 show the quite different damage levels,although the samples in these three typical tests were approximately subjected to the same incident wave.With bar/sample interfaces fully lubricated,the samples are completely fragmented into small pieces, featuring a typical splitting failure mode.This failure mode confrms 1D stress states during the dynamic tests.In contrast,with friction constrain at the boundary interfaces,the splitting is constrained signifcantly and the recovered samples feature a shear cone.It can be concluded that without proper lubrication,the measured strength values will be over-estimated and the failure mode will also be quite different.

5.2.Dynamic tension test

For rock materials,dynamic tension tests can be approximately categorized into two approaches:direct tension(Howe et al.,1974; Goldsmith et al.,1976;Huang et al.,2010a)and indirect tension (Klepaczko and Brara,2001;Wu et al.,2005;Schuler et al.,2006; Dai et al.,2008;Kubota et al.,2008;Wang et al.,2009;Zhou et al.,2012).For dynamic direct tension method,the specimen is subjected to dynamic tensile load which is directly generated by SHTB.The dynamic indirect tension method includes Brazilian disc (BD)method(Zhou et al.,2012),semi-circular bend(SCB)method (Dai et al.,2008)and spalling method(Klepaczko and Brara,2001; Wu et al.,2005;Kubota et al.,2008;Erzar and Forquin,2010).

5.2.1.Dynamic direct tension method

In order to generate directly dynamic tensile loading in specimen,the tensile versions of Kolsky bar system have been designed.The early design of dynamic tension experiments was a hollow tube,inside which incident and transmitted bars with a specimen sandwiched in between are placed(Hauser,1966; Harding and Welsh,1983)(Fig.22a).The principle of this device is to convert the external axial compression impact in external tube into tension wave in incident bar via the external tube where the Kolsky bar system is placed.This approach was just an extension of a compression version of Kolsky bar system and directly utilized the launching system of a compression bar system.However,since the whole setup was inside a solid tube,it is inconvenient for instrumentation(e.g.strain gauge)and direct observation of the specimen deformation.Then,a new confguration with top-hat specimen was proposed by Lindholm and Yeakley(1968),where a top-hat specimen is placed between the solid incident bar and the hollow transmission tube(Fig.22b). When the compression stress wave in the incident bar arrives at the specimen,a tensile load is produced on the specimen gauge section and a compression stress wave is transmitted into the transmitted tube.The advantage of this design is that the specimen does not need to be attached to the bar ends.Nicholas(1981) introduced a way to use only the compression bar system to achieve tensile experiments(Fig.22c).The modifcations include (i)the specimen which is threaded into the incident bar and transmitted bar,and(ii)a rigid collar placed over the specimen. The function of rigid collar allows the initial compression wave to pass through the collar without virtually touching the specimen and most of the initial compression energy is transferred into the transmitted bar.The transmitted compression wave is refected to be a tensile wave,and propagates back to load the specimen only because the collar cannot support tensile load.However,in this design,the specimen with the collar will inevitably deform when subjected to the initial compression wave.

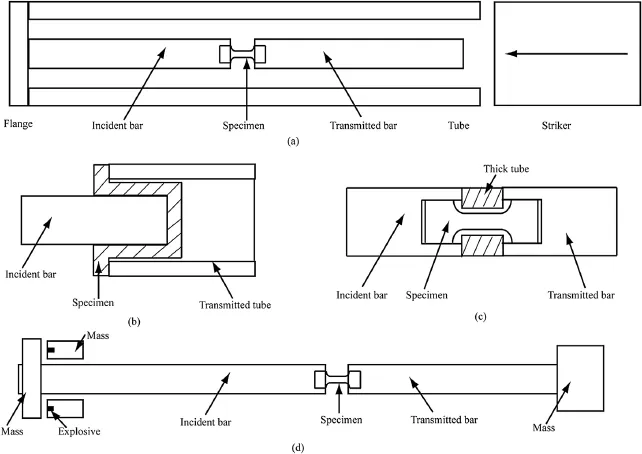
Fig.22.Schematics of four types of dynamic direct tension methods.

The most effcient loading method for Kolsky tension bar is direct tension.The frst way is to store elastic energy bystretching a section of incident bar in tension(Staab and Gilat,1991;Cadoni et al.,2009).A clamp is used to divide the pre-stressed and stress free section in the incident bar.Suddenly releasing or breaking theclamp can release the stored energy and produce tensile stress waves which load dynamically on the specimen in form of tension. Nevertheless,it is diffcult to control this sudden release of energy. The second way of direct tension loading is to impact a fange at the end of the incident bar.A rotating disk with an impact hammer is an approach to strike the fange(Kawata et al.,1979;Li et al.,1993). The hammer,which is released by a controller at a certain speed, impacts on the block which is linked with the incident bar by a fxed metal bar.This fxed metal bar is then fractured by stretching, which generates a tensile stress wave in the incident bar.Albertini and Montagnani(1974)used both a rapid fracture of a clamp in a pre-stressed bar and an explosive loading device to produce a tensile pulse into the incident bar(Fig.22d).Goldsmith et al.(1976) employed a ballistic impact to generate a tensile pulse.In this design,a short platewas attached toone end of theincident barand a ball was shot at the plate using a gas gun placed next to the bars. The tensile pulse in the bar may be accompanied by the bending wave which was generated by the asymmetric loading.

Another direct tension loading is to utilize a tubular striker to impact the fange of the incident bar.Sliding freely on the incident bar,the tube impacts on the fange attached to the end of the incident bar,producing a tensile stress wave(Ogawa,1984).The design is similar to the compression version of Kolsky bar except the tube striker and connection between the specimen and bars, and becomes the standard design of modern SHTB.

The SHTB system for measuring the dynamic tensile strength is shown in Fig.23,which consists of a striker tube,an incident bar,a transmitted bar,and two absorption bars.The stress pulse is measured by two strain gauges,which are mounted on the incident bar and the transmitted bar,respectively.For ductile material,the screw thread connection was widely utilized to employ the tension specimen in the bar system.This connection method usually induces inevitable gaps between specimen and bars,which causes multiple mini-impacts in the gaps and thus results in oscillations in stress wave and signifcanterror in data reduction.Thus,epoxyglue is used to attach the specimen to the incident bar and the transmitted bar,which signifcantly improves the quality of the waves. Two types of rock specimens for direct tensile test were designed: dumbbell-shaped specimen(Fig.24a)(Huang et al.,2010a)and bone-shaped specimen(Fig.24b)(Howe et al.,1974;Goldsmith et al.,1976).

The tensile force on both ends of the specimen can be calculated by Eq.(1)and the histories of stress,strain and strain rate can be obtained from Eq.(9).In order to achieve dynamic force equilibrium,the pulse shaping technique was used during dynamic loading.Fig.25 shows a typical tensile force without and with the pulse shaper,whereT1andT2are the tensile force on both ends of the specimen,respectively.Without the pulse shaper,the force mismatch betweenT1andT2exists,which induces error for tensile strength.However,with the pulse shapers,the dynamic force balance is achieved during entire loading period and the inertial effects thus can be eliminated.Since the impact surface is the crosssection of tube,two copper discs are placed symmetrically on the incident fange.The striker tube impacts the two copper discs prior to the incident fange.The deformation of two copper discs generates a smooth rising tensile pulse propagating into the incident bar.

Fig.26 shows the tensile strength values of Laurentian granite increasing with the increase of the loading rate.This trend is characterized by a linear ftting in Fig.26.

The nominal surface energy of Laurentian granite can be calculated by fracture energy and the area of the new surface.The fracture energy can be derived from the difference of the energies carried by the incident,refected and transmitted waves.Fig.27 illustrates that the surface energy increases with the loading rate. The physical mechanism of this loading rate dependence is of the same nature as the loading rate dependence of the fracture energy for the same rock(Huang et al.,2010a).The increases of the surface roughness and volumetric damage of materials adjacent to the fracture plane mainly contribute to the increase of fracture energy.

5.2.2.Dynamic indirect tension method

For dynamic direct tension methods discussed above,there are several limitations:(i)the requirement of alignment is very strict to avoid bending;(ii)the complex shape of the specimen for avoiding pre-mature failure leads to high cost of sample preparation;(iii)a proper high strength epoxy glue is required for joining the sample to the bar.The dynamic indirect tension methods not only providealternative to overcome the diffculties of dynamic direct tension methods,but also are convenient for instrumentation.

Fig.23.Schematics of an SHTB system and thex-tdiagram of stress waves propagation in SHTB(after Huang et al.,2010a).

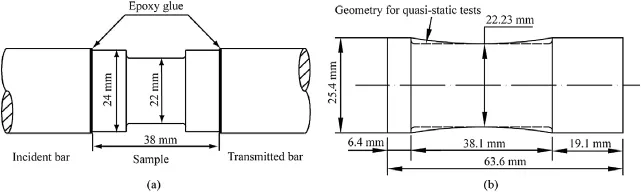
Fig.24.Schematics of two types of dynamic direct tension samples(unit:mm).

(1)Brazilian disc(BD)method

SHPB has also been adopted to conduct indirect tension tests for measuring the tensile strength of brittle solids like rocks.The BD method is based on the fact that the rock is much weaker in tension than in compression and thus the diametrically loaded rock disc specimen fails due to the tension along the loading diameter near the center.The BD specimen in the SHPB system is shown schematically in Fig.28a,where the sample disc is sandwiched between the incident bar and the transmitted bar.Provided a quasi-static state has been achieved in the sample during the test,the dynamic tensile strength is determined by the following equation (Iqbal et al.,2008):

whereσtis the tensile strength,Pfis the load when the failure occurs,andBis the disc thickness.Under quasi-static state,Pfcoincides with the maximum loading to the sample.

The conventional SHPB tests were conducted using the BD method on marbles(Wang et al.,2006)and argillites(Cai et al., 2007).These attempts followed the pioneer work on dynamic BD tests of concretes using SHPB(Ross et al.,1989,1995;Tedesco et al., 1989).The details of major development on the BD method using SHPB were reviewed by Zhang and Zhao(2014).

Fig.25.Dynamic force balance of SHTB test(a)without and(b)with the pulse shaping technique(after Huang et al.,2010a).

The BD method has been suggested by the ISRM as a recommended method for static tensile strength measurement of rocks (Bieniawski and Hawkes,1978).Using the BD method,Zhao and Li (2000)measured the dynamic tensile properties of granite using a hydraulic loading system.For quasi-static and low-speed BD tests, it is reasonable to use the standard static equation to calculate the tensile strength.For dynamic BD tests conducted with SHPB featuring stress wave loading,the application of the quasi-static equation to the data reduction is also verifed by numerical simulations(Hughes et al.,1993;Zhu and Tang,2006)and experimental methods(Gomez et al.,2001;Xia et al.,2011;Zhang and Zhao, 2013a).The condition under which the static analysis is valid is the satisfaction of dynamic force balance in dynamic BD tests. Gomez et al.(2001)utilized photoelastic method to obtain the photoelastic fringe patterns of Homalite-100 disc samples under both quasi-static and dynamic loading conditions.Both photoelastic fringe patterns showed that the stress equilibrium condition of disc samples is satisfed.Zhang and Zhao(2013a)employed DIC to gain high-speed image and dynamic strain felds of BD specimen of Fangshan marble,which demonstrates that the stress equilibrium on both ends of BD is also satisfed.Xia et al.(2011)investigated the stress equilibrium of BD specimens in the SHPB test using high-speed camera and numerical simulations.Fig.29 illustrates the time-varying forces in a typical test without pulse shaping and with careful pulse shaping technique.Without the pulse shaping, the generated incident wave is a square compressive stress wavewith a sharp rising edge,which inevitably introduces high frequency oscillations.Thus,the dynamic forces on both ends of the sample vary signifcantly and have a sizeable distinction betweenP1andP2.However,with the careful pulse shaping,it is evident that the time-varying forces on both sides of the samples are almost identical before the peak point is reached during the dynamic loading.The resulting force on either side of the sample also features a linear portion before peak,thus facilitating a constant loading rate via˙σ=2k2/（πDB）,where the parameterk2is illustrated in Fig.29.

Fig.26.Dynamic tensile strength of Laurentian granite(after Huang et al.,2010a).

Fig.27.Nominal surface energy of Laurentian granite as a function of the loading rate (after Huang et al.,2010a).

For avalid Brazilian test,the disc sample should break frst along the loading direction somewhere near the center of the disc (Shewmon and Zackay,1961;Hudson et al.,1972).To verify this,Xia et al.(2011)used a high-speed camera to monitor the fracture processes of the BD test.The failure process of the BD test without and with pulse shaping is shown in Fig.30.Without pulse shaping, the frst breakage emanates from the incident side of the sample after the incident wave arrives at the bar/sample interface.Soon after that,damages also occur from the transmitted side of the sample.Thus,the splitting of the disc is triggered by the damages at the loading points and then expands to the center of the disc.Since the cracking of the BD initiates from the loading ends,not from somewhere near the center of the disc,the working principle of a BD test is violated and the standard equation(Eq.(10))is invalid for reducing the tensile strength from the tensile stress history at the disc center.With pulse shaping,the BD sample achieves force balance.In sharp contrast to the images from the non-pulse shaped BD tests,this disc cracks near the center,then the fracture propagates bilaterally to the loading ends.The next two frames illustrate the splitting trajectory of the sample;and the disc specimen is split completely into two fragments approximately along the center line of the sample(Fig.30).Because the splitting of the disc initiates near the center,the tensile strength can be determined as long as we can accurately determine the tensile stress of the disc at failure.

Moreover,for conventional dynamic compression tests with SHPB or direct tension tests with SHTB,the samples are cylindrical and thus the force balance at the ends ensures the stress equilibrium throughout the sample.However,the disc is 2D;the force balance on the boundaries does not necessarily ensure dynamic equilibrium within the entire sample.A further comparison of the stress history at a point of interest from full dynamic analysis with that from quasi-static analysis is necessary.The histories of the stress components,σx(in tension)andσy(in compression),at the disc center(potential failure spot)for dynamic and quasi-static fnite element analyses are compared in Fig.31a and b,respectively.The stress states at the disc center from both quasi-static and dynamic data reductions match with each other.Hence the quasistatic analysis with the far-feld loading measured as input can accurately represent the stress history in the sample provided the force balance on the sample ends,and the standard BD equation (Eq.(10))can be used to reduce the tensile strength.

In quasi-static BD tests,although the BD sample may fracture before the peak load is reached,the difference between the peak load and the failure load may be smaller if a servo-controlled material testing machine is used and the transverse expansion of the disc is used as the controlling variable(Shewmon and Zackay,1961; Hudson et al.,1972).In dynamic BD tests using SHPB,there is no way to control the load using a feedback system,thus the mismatch of the measured peak load and the failure load can be signifcant. Fig.32 shows the signal of the strain gauge mounted on the position at 10 mm distance from the center of the BD sample,compared with the transmitted force for a test featuring high loading rate.It can be concluded that the tensile stress at the fracture onset(namely tensile strength)is much lower than the peak stress determined from the far-feld loading.The reason for this phenomenon lies in the sample test confguration.For an ideal BD test, the fracture will initiate at the center of the sample along the loading axis.At the fracture onset,the sample is still in contact with the two loading platens.The load can thus still increase until the sample is completely split into two halves.From part of the strain energy release from the fracture,the two halves will get transverse velocities to separate from each other.The two halves may rotate and lose contact with the platen during the separation process, resulting in unloading.

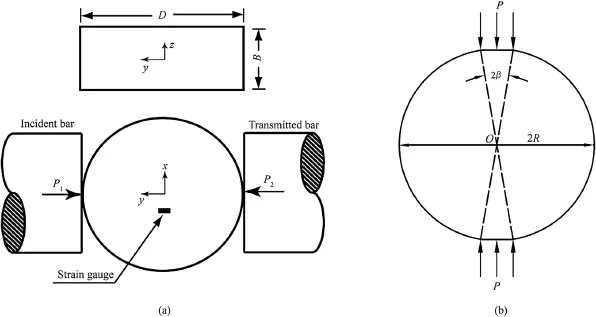
Fig.28.Schematics of Brazilian disc and fattened Brazilian disc.

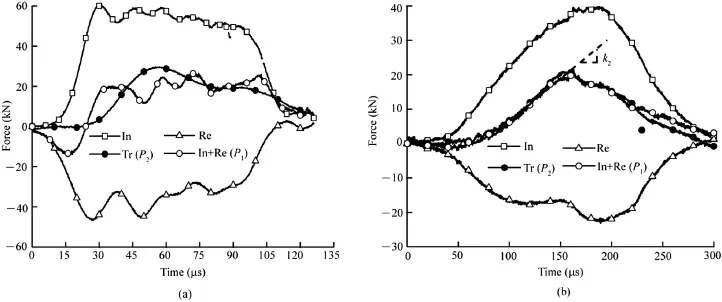
Fig.29.Dynamic forces on both ends of disc specimen tested using a modifed SHPB:(a)without pulse shaping and(b)with careful pulse shaping(after Dai et al.,2010b).

The post-mortem failure patterns of BD samples in SHPB tests generally consist of two types:shear failure and tensile failure (Zhang and Zhao,2013a;Zhou et al.,2013).The tensile failure is the main axial crack parallel to the impact direction,dividing the sample into two pieces.The shear failure zones are at the contact points of BD,which are more signifcant with the increase of loading rate.As shown above,for a valid dynamic BD test,the failure should start from the center of the disc.The shear failure is then a result of secondary fractures due to further compression between the bar and the cracked disc as demonstrated by the highspeed camera snapshots.However,due to misunderstanding of the failure process,fattened BD method was proposed to prevent the shear failure zone as shown in Fig.28b(Wang et al.,2009).The principle of the fattened BD method is similar as that of BD method.However,as discussed,there is no need to prevent the shear failure as long as the initial failure starts from the center of the disc,and this approach has also other limitations(Yu et al., 2009).

(2)Semi-circular bend(SCB)method

SCB was also used in SHPB to measure the tensile strength of Laurentian granite(Dai et al.,2008,2010a)The SCB specimen in the SHPB system is shown schematically in Fig.33 and the insert of Fig.34.The pulse shaping technique was employed to achievedynamic force balance and momentum-trap technique was used to attain single-pulse loading.

Fig.30.High-speed video images of two typical dynamic Brazilian tests.Top four images:Brazilian test without pulse shaping;Bottom four images:Brazilian test with careful pulse shaping(after Xia et al.,2011).

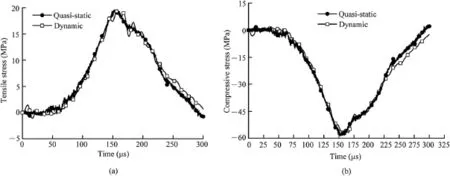
Fig.31.(a)Tensile stressσxand(b)compressive stressσyhistories at the Brazilian disc center from both dynamic and quasi-static fnite element analyses in a typical SHPB Brazilian test with pulse shaping(after Xia et al.,2011).

Provided a quasi-static state has been achieved in the sample during the test,using a dimensional argument,the equation for calculating the tensile stress atOis(Dai et al.,2010a):

whereP(t)is the time-varying load recorded in the test,Sis the span of the supporting pins,andRis the radius of the disc.The dimensionless stressY(S/(2R))can be calibrated using fnite element analysis.The dynamic tensile strength measured by the SCB method is also called fexural strength,and the fexural tensile strengthσfis taken as the maximum tensile stress in the history of σ(t)and the corresponding loading rate is measured from the slope of the pre-peak linear portion of the curve.The reason why strengths measured using the SCB method are higher than those by the BD is initially explained using a non-local failure model(Dai et al.,2010a).Since the dynamic force equilibrium is satisfed in all SCB tests,the non-local failure approach should work for dynamic SCB and BD tests.This theory states that the material fails when the local stress averaged over a distanceδalong the prospective fracture path,σ,reaches the tensile strength,σt(Lajtai,

Fig.32.Tensile stress history with the strain gauge singal for detecting failure onset (after Xia et al.,2011).

1972;Car∫ter,1992;Van de Steen and Vervoort,2001): σ=（1/δσdl,where l0is a characteristic material length σ δ scale,andis the tensile stress distributing over.Numerical methods were applied to calculate σfor a given sample geometry. The tensile stress gradient(the ratio of the tensile stress along the prospective fracture path,σ,to the tensile stress at the failure spot, σm(also the maximum tensile stress in the sample)along the prospective fracture path of SCB sample was calculated numerically with fnite element analysis,and then the relation between σand σmcan be found.Thus,at the critical state,the fexural tensile strength,σf,is equal toσmand the tensile strength,σt,from BD test is equal to σ.The relation betweenσfandσtcan be established. Using this relation and non-local failure theory,the tensile strength σtcan be derived from the measured dynamic fexural strengthσf(Dai et al.,2010a).Dai et al.(2010a)demonstrated that the corrected dynamic tensile strengths from fexural strengths have a good agreement with those measured from the dynamic BD tests (shown in Fig.34).The rate dependence of dynamic tensile strength for Laurentian granite is demonstrated in Fig.34(Dai et al.,2010a). Besides,the simulated fracture pattern from fnite-discrete element method agreed well with that from the recovered specimen(Dai et al.,2010a).However,the results obtained from the SCB test is the fexural strength,which is different from the tensile strength from the BD method(Zhang and Zhao,2014).

(3)Spalling method

The spalling method on SHPB is based on the refection of elastic wave in a cylindrical bar(Fig.35).A compressive wave propagates into a cylindrical specimen and is refected as a tension wave at the free end of specimen.Since the tensile strength of rock is muchlower than its compressive strength,the refected tension wave causes the failure of rock specimen.

Fig.33.Schematics of the SCB method.

Fig.34.Rock tensile strength of Laurentian granite measured using BD and SCB methods in SHPB system(after Xia,2012).

The spalling method is widely used to obtain the tensile strength of brittle materials(Klepaczko and Brara,2001;Wu et al., 2005;Kubota et al.,2008;Erzar and Forquin,2010).However,the spalling method has some limitations:(i)the incident compressive wave may infuence the specimen properties before the tensile wave;(ii)the 1D stress state is diffcult to be ontained;(iii)the stress wave attenuates in the rock materials.

5.3.Dynamic shear tests

Shear strength is an important material parameter for rocks.The dynamic shear strength of Barre granite was frstly determined using solid cylindrical specimens in torsional split Hopkinson bar (Goldsmith et al.,1976).Then,the torsional split Hopkinson bar with thin-walled tubes was utilized to obtain the pure shear strength,as shown in Fig.36a(Lipkin et al.,1977,1979).The details of torsional split Hopkinson bar can be found in the ASM handbook (Gilat,2000).Although the torsional split Hopkinson bar overcomes the friction and lateral inertia effects(Gilat,2000),it is diffcult to prepare the thin-walled specimens and mount them on the bars.Therefore,several other methods have been developed to perform the dynamic shear tests,e.g.compression shear method (Rittel et al.,2002),punch shear method(Zhao et al.,1998;Huang et al.,2011a),and a split Hopkinson pressure shear bar(SHPSB) system(Zhao,2011).

The compression shear method was used for large strain test in SHPB.The SHPSB system consists of a wedge-shaped end incident bar and two transmitted bars,using quartz transducers and an optical system to obtain shear strength and shear strain.Dynamic punch shear method is widely used to measure dynamic shear strength and to study adiabatic shear band of materials.Zhao et al. (1998)employed the punch shear tests to measure the shear strength of Bukit Timah granite at loading rates of 10-104MPa/s using a pneumatic-hydraulic machine,which can neglect the wave propagation effects.Huang et al.(2011a)developed a dynamic punch shear method in SHPB to measure the dynamic shear strength of rocks(Fig.36b).

Fig.35.Dynamic tension tests by the spalling method.

Conventional punch shear systems for static tests have two types of punch head:the cylindrical punch head and the block punch heads.For dynamic tests,the incident bar plays the role of punch head,thus usually an annular holder is adopted(Li et al., 2002;Dabboussi and Nemes,2005;Qu et al.,2005).In the dynamic design,the sample assembly is composed of a front cover,a disc sample and a rear supporter(Fig.36b).The purpose of the front cover is to reduce the bending force during test and to prevent additional damage to the specimen after test.The inner diameter of holder is 0.4 mm larger than that of bars.ATefon adaptor is used to connect the rear holder to the transmitted bar(Huang et al.,2011a). The hole in the rear supporter recovers the sample after the shear test.

When the tests are under force equilibrium condition,i.e.P1=P2,the punch shear stress in samples is then calculated using the following equation:

whereτis the punch shear stress,andPis the loading force.The maximum value ofτis considered as the punch shear strength of the testedsample.The loading rate is determined as the slope of the punch shear stress curve.

Dynamic punch experiments on Longyou sandstone were conducted at different loading rates to investigate the rate effect on tensile strength.All tested samples were punched into a ring and a plug as shown in Fig.37.

The variation in the punch shear strength as a function of the loading rate is illustrated in Fig.38.It is evident from the fgure that the strengths of Longyou sandstone increasing with loading rates have been achieved.

5.4.Dynamic fracture tests

Dynamic fracture is frequently encountered in various geophysical processes and engineering applications(e.g.earthquakes,airplane crashes,projectile penetrations,rock bursts and blasts).These processes are governed by material dynamic fracture parameters,such as initiation fracture toughness,fracture energy, propagation fracture toughness,and average fracture velocity. Therefore,accurate determination of these fracture parameters is crucial for understanding mechanisms of dynamic fracture.

Under quasi-static loading conditions,the existing studies on material fracture are mainly focused on the initiation fracture toughness measurement.Initiation fracture toughness is defned as the material resistance to crack reactivation.Special sample geometries have been developed for initiation fracture toughness measurements for brittle solids like ceramics and rocks,which are different from the standard methods of fracture tests developed for metals.The ISRM recommended four suggested methods with four types of core-based specimens for determining the initiation fracture toughness of rock under quasi-static loads:chevron bend(CB) and short rod(SR)specimens method(Ouchterlony,1988),cracked chevron notched Brazilian disc(CCNBD)specimen method(ISRM, 1995),and NSCB specimen method(Kuruppu et al.,2014).

Fig.36.Schematics of(a)the torsional split Hopkinson bar(Gilat,2000;Zhang and Zhao,2014)and(b)the sample assembly for dynamic punch shear(after Xia,2012).

Since Bieniawski(1968)introduced the fracture dynamics of rock,various investigations have indicated that the fracture behavior of rocks under dynamic loading is remarkably different from that under quasi-static loading.Klepaczko et al.(1984) originally performed the wedge loaded compact tension(WLCT) method with the SHPB to measure the dynamic initiation fracture toughness.In their tests,the friction and stress equilibrium was discussed and the results demonstrate that the dynamic initiation fracture toughness of coal is about 13 times higher than the quasistatic value.Tang and Xu(1990)tried to measure the dynamic fracture toughness of rocks using single edge notched bending (SENB)method in three-point impact test with a single Hopkinson bar.The SENB method with a single Hopkinson bar was extensively discussed by Jiang and Vecchio(2009).Moreover,Nakano et al. (1994)introduced cracked straight through Brazilian disc(CSTBD) method to evaluate the dynamic fracture toughness and SIF of ceramic under mode I and mixed mode I/II loading conditions. Dong et al.(2004,2006)theoretically analyzed the CSTBD method and utilized this method to obtain the fracture behavior of polymethyl methacrylate(PMMA).The CSTBD method was subsequently modifed to fatten BD type and employed to determine the dynamic fracture toughness and SIF of rock materials under mode I and mixed mode I/II loading conditions(Wang et al.,2011a). Furthermore,Lambert and Ross(2000)developed a holed-notched cylinder fracture(HNCF)specimens with SHPB to obtain the dynamic fracture toughness of concrete.Finite element analysis verifed the experimental confguration and ultra-high-speed digital photography was synchronized with the fracture process to validate the experimental technique as a tool in determining the dynamic fracture toughness of quasi-brittle materials.The results show that the effective fracture toughness increases signifcantly with the loading rate.

Fig.37.(a)Typical tested and untested samples.(b)The ring and plug produced by the punch shear test(after Huang et al.,2011a).

The SR method was extended to dynamic fracture toughness testing with the SHPB technique by Zhang et al.(1999,2000).The results show that the maximum value of dynamic fracture toughness of Fangshan gabbro and Fangshan marble is about 20 and 40 times higher than the quasi-static value,respectively.However,the stress equilibrium condition is violated due to the stress wave loading and non-uniform deformation.Recently,the CCNBD method(Iqbal et al.,2008;Dai et al.,2010c),cracked chevron notched semi-circular bend(CCNSCB)method(Dai et al.,2011)and NSCB method(Chen et al.,2009;Dai et al.,2010d;Huang et al., 2011b;Zhang and Zhao,2013a)were extended to measure the dynamic fracture toughness and strain feld of brittle materials.

There are totally eight methods for dynamic initiation fracture toughness tests using the SHPB:WLCT,SENB,CSTBD,HNCF,SR, CCNBD,CCNSCB and NSCB methods.The NSCB method using the SHPB technique is an ISRM suggested method(Zhou et al.,2012).A summary of classic dynamic testing methods for the dynamic fracture properties of rock-like materials using split Hopkinson bar system is presented in Table 1.For brittle materials,the experimental methods of dynamic fracture toughness using the SHPB have been discussed by Ravi-Chandar(2004),Jiang and Vecchio (2009),and Zhang and Zhao(2014),but there is no systematic discussion of the experimental procedures of these methods.

Fig.38.Punch shear strength of Longyou sandstone vs.test loading rate(after Huang et al.,2011a).

Table 1A summary of classic dynamic testing methods for the dynamic fracture properties of rock materials using split Hopkinson bar system.

It should be noted that the dynamic fracture toughness and SIF in rock testing are determined by deformation feld measurement (strain gauge/caustics/high-speed DIC)(Nakano et al.,1994;Wang et al.,2010,2011a;Zhang and Zhao,2013a)or quasi-static fracture formulas(Klepaczko et al.,1984;Tang and Xu,1990;Zhang et al., 1999;Chen et al.,2009;Dai et al.,2010c,2010d,2011;Lambert and Ross,2000;Zhang and Zhao,2013a).The former is recommended to evaluate the processes of crack initiation and propagation,while the latter is a measurement of stress state,which can be conveniently obtained from incident,refected and transmitted pulses in the SHPB tests.

It is worth mentioning that the prerequisite that the evolution of dynamic SIF and the fracture toughness can be calculated by quasistatic fracture formulas is that the dynamic force balance is roughly achieved(Owen et al.,1998).Without the dynamic force equilibrium,the measured crack tip SIF history using a three-point bending confguration loaded by a drop weight did not synchronize with the load histories at supports due to inertial effect under high loading rate(Böhme and Kalthoff,1982).To facilitate dynamic force equilibrium and thus minimize inertial effect,the pulse shaping technique was employed to conduct dynamic fracture tests with the SHPB(Weerasooriya et al.,2006;Jiang and Vecchio,2007). The fracture sample istherefore in aquasi-staticstate of deformation.

The crack fracture velocity,dynamic fracture energy and the propagation fracture toughness of materials are directly related to the energy consumption during dynamic failures.For transparent polymers or polished metals,those properties could be readily measured with optical methods(Owen et al.,1998;Xia et al.,2006). For rocks,several methods to measure these fracture properties are also reported in the literature,e.g.the NSCB/CCNBD/CCNSCB method with LGG system was used to measure the crack fracture velocity,the dynamic fracture energy and the propagation fracture toughness(Chen et al.,2009;Dai et al.,2010c,2011);the NSCB method with crack gauge and/or DIC method was applied for obtaining the crack fracture velocity and the dynamic fracture energy(Bertram and Kalthoff,2003;Zhang and Zhao,2013b);the SR specimen with high-speed camera was utilized to analyze the dynamic fracture energy(Zhang et al.,2000).

5.4.1.NSCB method

NSCB test was adopted to measure dynamic fracture parameters of rocks(Chen et al.,2009).The NSCB specimen has the semicircular shape and it is made by splitting the rock disc into two halves,followed by machining a notch from the center of the disc perpendicular to the diametrical cut.Fig.39 shows the sandwiched NSCB fracture sample in the SHPB system and the LGG system.

A fundamental prerequisite for fracture testing via this NSCB specimen is the fabrication of a sharp crack.A notch was frst made in the semi-circular rock disc and then sharpened with a diamond wire saw to achieve a tip.For rocks with average grain size of 0.5 mm and larger,the radius of the tip is smaller than the thickness of naturally formed cracks in this rock.This will lead to a valid fracture toughness measurement(Lim et al.,1994).Compared to coarse-grained rocks,it is diffcult for fner-grained rocks to make a sharp enough crack tip.

Based on the ASTM Standard E399-90(2002)for rectangular three-point bending sample,a similar equation for calculating the SIF for mode I fracture in the NSCB specimen was proposed(Chen et al.,2009):

whereais the crack length.The dimensionless geometric functionY(a/R)depends on the crack geometry,and can be calculated with a standard fnite element software package(e.g.ANSYS).Fracture toughnessKICis obtained at the maximum load.

In a conventional SHPB test,without the pulse shaper,impact of the striker on the incident bar generates a square incident stress wave with a large fuctuation of dynamic force on the incident side.With a pulse shaper,the incident wave is shaped to a ramp pulse and the dynamic forces on both ends of the specimen are balanced.

The measured crack surface opening displacement(CSOD)of the NSCB specimen by the LGG,strain gauge signal and the transmitted force with the pulse shaper is illustrated in Fig.40.There is a single peak pointAin the transmitted force and only one troughBsignal is registered by the strain gauge.Thus,the fracture initiation time is designated by the unique troughB.Because the peak transmitted force is attained only 4μs after the measured fracture onset,it is demonstrated that the peak far-feld load matches with the fracture onset with negligibly small time difference.The small time difference between them can be partially interpreted as follows.The load on the specimen increases with the incident pulse before it reaches the peak.At the fracture onset,release waves are emitted from the crack tip at the sound speed of the rock material. The frst release wave takes time to reach the supporting pins due to the distance between the crack tip and the supporting pin.Thus, the small time difference occurs,leading to a negligibly small error in the fracture toughness.

Fig.39.Schematics of NSCB specimen in the SHPB system with LGG system(after Chen et al.,2009).

With a 2D geometric confguration,the dynamic force balance on the boundaryof the NSCB sample does notnecessarilyguarantee the dynamic stress equilibrium in the entire specimen.Thus,the comparison between the SIF evolution obtained from the dynamic fnite element analysis and the result from a quasi-static analysis is evaluated(shown in Fig.41).The evolutions of SIF from both static and dynamic methods match reasonably well,and the quasi-static equation is thus valid for determining the fracture toughness in SHPB test with pulse shaper.

Therefore,with dynamic force balance in SHPB,the peak farfeld load coincides with the fracture onset and the maximum load corresponds to the failure load.The fracture toughness can thus be confdently deduced from the peak far-feld load by virtue of quasi-static equations.The inertial effects are eliminated since there is no global force difference in the specimen to induce inertial forces(Weerasooriya et al.,2006).Hence,fnite element analyses with the dynamic far-feld loading were conducted to obtain the local SIF at the crack tip for a given specimen geometry.Singular element(Barsoum,1977)is applied to the vicinity of the crack tip in meshing the fnite element model.The load is set as the boundary stresses at the left and right edges of the model plate while the lower edge of the model has the symmetric boundary condition. The resulting loading at the main crack is mode I.For a given loadP,KIcan be obtained from the fnite element analysis.

Fig.40.Comparison of CSOD and strain gauge signal on the specimen with the transmitted force of the NSCB specimen tested using pulse shaper(after Xia et al., 2011).

Moreover,a high-speed camera,which was placed perpendicular to the SHPB and specimen,was used to monitor the fracture initiation and propagation process as well as the trajectories of the fragments(Chen et al.,2009).The sequence of high-speed camera images shown in Fig.42 represents only the frames of representative features.The frst two images show the pre-fabricated notch and the crack opening can be barely seen.Next,the opening of the NSCB crack becomes visible.Then,the NSCB specimen is split completely into two fragments.The fragments then rotate about the contact point between the specimen and the incident bar.The measured rotation angle of the fragment indicates that the angular velocity of the fragments is almost constant during the period,and the fragments rotate around the axis along the loading point.

The energy conservation principle can be used to calculate the propagation fracture energy and fracture toughness,which were used with a high-speed camera to estimate the fragment residual velocities(Zhang et al.,2000).Zhang et al.(2000)estimated the kinetic energy of the fragments in SR test asK=0.5m（v21+v22）.The total energy absorbed by the sample can be calculated byWs=WIn-WRe-WTrsince the energy loss at the interfaces between the specimen and the bars can be negligible.Then,the fracture and damage energy can be obtained:WFD=Ws-K.Hence, in this NSCB test,the elastic energycarried bya stress wave is(Song and Chen,2006):

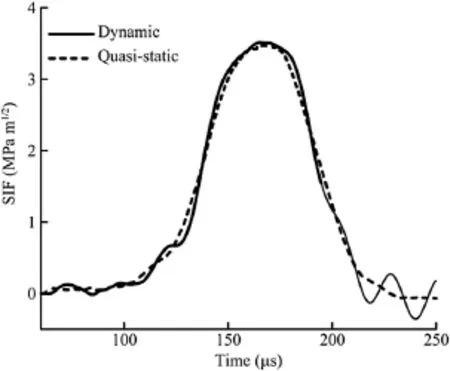
Fig.41.The evolution of SIF of the NSCB specimen with both quasi-static and dynamic analyses tested using pulse shaper(after Zhou et al.,2012).

Fig.42.Selected high-speed camera images showing the fracture and fragmentation of an NSCB specimen(after Chen et al.,2009).

The totalenergy absorbed by the specimen then is ΔW=WIn-WRe-WTr.Part of the total energy absorbed is used to create newcrack surfaces,called the total fracture energy(WG);and the other part remains in the fragments as the residue kinetic energy(K),i.e.ΔW=WG+K.For the rotating fragments,the moment of inertia isI,and the total rotational kinetic energy isK=Iω2/2, where the fragment angular velocityωis estimated from the CSOD data.The average propagation fracture energy isGc=WG/Ac,whereAcis the area of the crack surfaces created.The average dynamic propagation fracture toughness is

Here the plain strain condition is assumed.This method provides a promising way to estimate the dynamic propagation fracture toughness,which can also be used in the CCNBD method(Dai et al.,2010c)and CCNSCB method(Dai et al.,2011).Besides,the dynamic SIF was also estimated by using a chain of strain gauges positioned along the prospective crack propagation path(Zhang and Zhao,2013b).The measured dynamic fracture propagation toughness is about ten times higher than the dynamic initiation fracture toughness.

5.4.2.CCNBD method

The NSCB method requires a sharp notch,which is diffcult to be achieved for fne-grained rocks.To address this problem,a convenient way in the fracture test is to employ a sample with a V-shaped(or chevron)notch as suggested by the ISRM(Ouchterlony, 1988;ISRM,1995).TheV-shaped ligamentfacilitatescrack initiation emanating from the notch tip and thus avoids precracking in the brittle solids.Subsequently,for a V-shaped(or chevron)notch specimen,the crack propagates in a stable fashion until it reaches the critical crack length where the crack transfers to unstable growth.If the load is static,the load reaches its maximum at this critical crack length while the corresponding SIF has a minimum value.The V-shaped notch specimen has been conducted in the SHPB fracture test for rocks(Zhang et al.,1999, 2000)and ceramics(Weerasooriya et al.,2006).The quasi-static equation proposed in the ISRM(Ouchterlony,1988)method was employed to determine the fracture toughness without evaluating the stress state in the sample.

The CCNBD method has been suggested by the ISRM as one of static fracture toughness measurement methods.Among three standard ISRM specimens(Ouchterlony,1988;ISRM,1995),the CCNBD specimen owns special merits such as:much higher failure load,fewer restrictions on the testing apparatus,larger tolerance on the specimen machiningerror,simpler testingprocedure and lower scatter of test results(ISRM,1995).This CCNBD method has been widely used(Dwivedi et al.,2000;Iqbal and Mohanty,2007).It has also been employed for dynamic fracture toughness measurement in the SHPB.

Fig.43 shows the schematics of the SHPB system and the LGG system.The geometry of the CCNBD sample is shown in Fig.44.The CCNBD specimen is produced by two symmetric cuts on the ends,a rock disc perpendicular to the end and through one diametrical direction.The basic assumption of the method is that the fractures initiate and propagate symmetrically from the two tips of the ligaments.As compared with the NSCB method,the CCNBD method can be applied to fne-grained rocks,for which it is very diffcult to fabricate sharp notches(Dai et al.,2010c).

With the pulse shaping technique in dynamic CCNBD tests,the dynamic forces on both loading ends of the sample are almost identical throughout the dynamic loading period,and the inertial effects are thus eliminated because there is no global force difference in the specimen to induce inertial force.Then,a quasi-static state of the specimen has been achieved during the SHPB test, the initiation fracture toughnessKICof CCNBD specimen is determined by the ISRM suggested method(ISRM,1995):

Fig.43.Schematics of CCNBD specimen in the SHPB system and LGG system(after Dai et al.,2010c).

wherePmaxis the measured maximum load,Ym*inis the minimum value ofY*,andY*is the dimensionless SIF and can be determined in advance by numerical calibrations according to the following equation:

As a critical factor for determining fracture toughness,Ym*incorresponds to the dimensionless SIF at the critical dimensionless crack lengthαm(αm=am/R,amis the critical crack length),where the load is maximum.

For a given CCNBD sample confguration,the critical dimensionless SIF,Ym*in,can be found by the ISRM suggested method (ISRM,1995).However,the corresponding critical dimensionless crack length,αm,is not explicitly documented(ISRM,1995).A fnite element analysis is used to determine the critical dimensionless crack length,αm,and the corresponding dimensionless SIF,Ym*in(Fig.45).

Fig.44.The CCNBD specimen in an SHPB system,whereRis the radius of the disc,Bis the thickness of the disc,Rsis the radius of the diamond saw for making notch,ais the length of crack,a0is the initial half-length of chevron notch,anda1is the fnal half-length of chevron notch(after Dai et al.,2010c).

Fig.45.The calculated dimensionless SIF varying with the dimensionless crack length α(after Dai et al.,2010c).

Then,the fracture energy can be calculated in a similar way as described in Section 5.4.1.The only difference lies in the calculation of the residual kinetic energyKin the two cracked fragments.In the CCNBD test,the sample is cracked completely into two half discs after the crack propagates through the sample.The experiments indicate that the failure of the specimen is symmetric.Consequently,the movement of fragments is translation motion without rotation,and thus the total kinetic energy was calculated by adding the translational kinetic energy of the two fying fragments.The kinetic energyKfor CCNBD test can be calculated withK=mvt2/2, wheremis the mass of the specimen,vtis the translationvelocityof the fragments,which can be deduced from the CSOD history data measured by the LGG system.

Fig.46 shows the CSOD measured by the LGG system as well as the strain gauge signal mounted on the sample,compared with the transmitted force(P2)in the SHPB test.With dynamic force balance, the transmitted forceP2can be regarded as the loading to the sample,similar to the quasi-static case.The strain gauge signal of the sample surface is used to detect the fracture initiation and propagation.The fracture initiation from the notch tip will result in a decrease in the strain gauge signal,denoted as pointCin Fig.46. This fracture initiation coincides with the turning pointAin the sustaining loadP2.After this instant,to further drive the propagation of the crack,the load has to increase until the peak pointB.At this instant,the crack reaches the critical crack length(with dimensionless crack lengthαm)and the unloading starts due to transition of crack growth from stable to unstable.The peak of the loading corresponds to the moment that the crack reaches the critical crack length.The delay in time between pointsBandDattributes to the time that the frst release wave propagates from the crack tip to the transmitted end of the specimen.It is noted also that the measured CSOD curve by the LGG system exhibits an obvious linear segment after pointE.The slope of this linear segment indicates constant departure velocity of the two fractured fragments.The pointEthus designates the complete separation of the two fragments of the CCNBD specimen.

Fig.46.LGG measured CSOD and strain gauge signal of the CCNBD sample surface, compared with the transmitted force in the SHPB test with pulse shaping(after Dai et al.,2010c).

The dynamic fracture process of the CCNBD specimen in the SHPB test can be divided into four stages,separated by three vertical lines through pointsA,B,andE(denoted by I-IV in Fig.46). The elastic deformation of the CCNBD specimen dominates stage I. At the end of stage I,the crack initiates from the notch tip,and propagates until the crack reaches the critical crack lengthαm(stage II).PointBdesignates the transition of stable to unstable crack propagation.During stage II,the crack propagates stably; while in stage III,the crack propagates unstably.Finally,the sample is cracked completely into two half fragments in stage IV fying away from each other.

The measured fracture initiation toughness values by the dynamic CCNBD method are compared with those obtained from dynamic NSCB tests in Fig.47.The fracture initiation toughness is quite consistent with the measured results by the NSCB.

5.4.3.CCNSCB method

As shown in Fig.48,the CCNSCB specimen is a combination of the NSCB specimen and the CCNBD specimen.The CCNSCB method is advantageous in that it does not need a sharp pre-crack as in the NSCB method and involves only one fracture(Dai et al.,2011).Just like the CCNBD method,the CCNSCB method can be applied to fnegrained rocks.In the CCNBD method,it is assumed that the two fractures should initiate at the same time and propagate symmetrically.Thisassumption can be easily violated due to inhomogeneities in the rock sample and misalignment.The CCNSCB method overcomes this problem by involving only one fracture.

The geometric detail of the CCNSCB specimen is shown in Fig.48.The CCNSCB specimen is sandwiched between the incident and transmitted bars.Rock cores are frst drilled from the rock blocks and then sliced to obtain disk samples.All disk samples are polished afterwards resulting in a surface roughness variation of less than 0.5%of the sample thickness.By diametrical cutting,half disc samples are subsequently made from the full discs.A diamond impregnated blade saw is used to fabricate the notch near the diametric cut of the half discs.A strain gauge is cemented on the sample surface to monitor the fracture initiation and propagation during the test(Jiang et al.,2004).

Fig.47.Comparison of the initiation toughness from CCNBD-SHPB and NSCB-SHPB methods(after Xia et al.,2011).

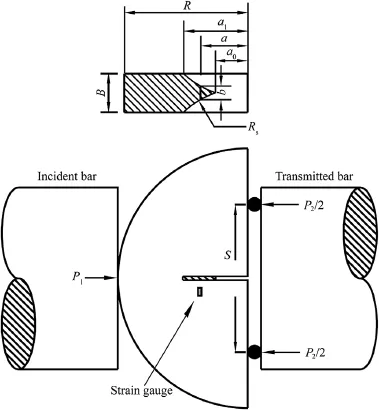
Fig.48.Schematic of the CCNSCB specimen in the SHPB system,whereSis the distance between the two supporting pins(after Dai et al.,2011).

Provided a quasi-static state of the specimen has been achieved during the SHPB test with careful pulse shaping,the fracture properties can be reduced using a quasi-static data analysis based on the theory of linear elastic fracture mechanics(Dai et al.,2010d). Similar to the calculation equation suggested by the ISRM for the NSCB specimen and the CCNBD specimen(ISRM,1995;Zhou et al., 2012),the initiation fracture toughness,KIC,of CCNSCB specimen can be determined as

It is noted that this formula is different from that proposed before(Dai et al.,2011).Since there is only one design of the sample dimension,the result is independent of the form of the formula.

The dynamic fracture toughness values measured by the CCNSCB method for Laurentian granite are compared with those by the CCNBD method(Fig.49).There are two fracture toughnesses in the fgure:propagation fracture toughness and initiation fracture toughness.The initiation fracture toughness is the commonly used fracture toughness.The propagation fracture toughness is equal to the SIF of a propagating fracture,which characterizes the material resistance against a dynamically propagating fracture.The propagation fracture toughness may vary with the loading rate or the fracture velocity(Bertram and Kalthoff,2003).

5.5.Dynamic testing methods at various temperatures

Temperature is one of the main factors affecting the mechanical properties of rock materials,and it plays a signifcant role in many engineering practices.Experimental results show that the temperature markedly infuences the compressive strength,tensile strength and fracture toughness of rock materials(Paterson and Wong,2005).Under quasi-static loading,the strength of rock material decreases with temperature.The effects of temperature and loading rate on rock strength and rock fracture toughness are also investigated.

Fig.49.Comparison of the initiation fracture toughness and the average propagation fracture toughness from the CCNSCB method with those from the CCNBD method (after Dai et al.,2011).

The study of Perkins et al.(1970)demonstrated that the stiffness and strength of porphyritic tonalite increase with increasing strain rate and decreasing temperature.Lindholm et al.(1974)utilized the SHPB to measure the uniaxial compressive strength of Dresser basalt with ambient temperatures of up to 527°C and obtained an equation with respect of the ambient temperature,the strain rate, and the fow stress.Zhang et al.(2001)measured the dynamic fracture toughness of Fangshan gabbro and Fangshan marble under high ambient temperatures and room temperatures with an SR specimen in the SHPB system.Theyconcluded that the temperature has a limited infuence on the dynamic fracture toughness of such rocks within the limited temperature range(up to 330°C).Li et al. (2010)conducted the SHPB experiment to investigate the dynamic strength of siltstone under temperatures from 20°C to 300°C.The results show that the dynamic peak strength of siltstone increases with the increase of temperature.However,the strength of siltstone decreases with the increase of temperature when the temperature is over 100°C.Fang et al.(2012)performed the SHPB experiment to obtain the compressive strength of slat rock under temperatures from 40°C to 80°C.The result shows that the compressive strength decreases as the temperature increases under the high strain rate of 400 s-1.Liu and Xu(2013)carried out the SHPB experiment with high temperature device to study the uniaxial compressive strength of marble.The results demonstrate that the peak stress fuctuates slightly between 25°C and 400°C but decreases nearly linearly when the temperature is over 400°C.

The SHPB experimental setup with high temperature device is shown in Fig.50,which mainly includes a striker,an incident bar,a transmitted bar,an absorption bar and a furnace.After the specimen was mounted on the SHPB system,a furnace started to heat the specimen at a desired heating/cooling rate.The temperature in the furnace could be automaticallycontrolled with a high precision. As soon as the temperature in the furnace reached the assigned value,the temperaturewas keptfora short period sothat thewhole specimen from the outside to the inside could be heated/cooled to the appointed temperature(Li et al.,2010;Fang et al.,2012).Then the striker bar was launched,and the specimen was tested under a dynamic loading condition.In order to achieve dynamic force equilibrium,the pulse shaping technique was used during dynamic loading.The forces on both ends of the specimen can be calculated by Eq.(1)and the strength or fracture properties of specimen arethen obtained.After the test,the specimen was collected and cooled down in the air.Since the temperature gradient in bars generally infuences wave propagation and induces the errors to the rock strain rate,rock temperature and time,the wave propagation in the bars has to be corrected during data reduction(Zhang and Zhao,2014).

Fig.50.Schematics of an SHPB system with high temperature device(Li et al.,2010;Fang et al.,2012).

Another method is to study the effect of heat treatment on the mechanical properties of rock materials.Yin et al.(2012)performed the dynamic NSCB tests with the SHPB system to measure the dynamic fracture toughness of Laurentian granite with different temperatures.Except for a control group of samples without thermal treatment,the samples were thermally treated at 100°C, 250°C,450°C,600°C,and 850°C.The thermal treatment was carried out in a servo-controlled electrical furnace with a designed heating/cooling speed,which is suffciently slow to avoid cracking due to thermal shock.The ultrasonic P-wave velocity of samples are changed after the thermal treatment since the heating introduces damage to rocks in the form of micro-cracks and the ultrasonic P-wave velocity of rocks is sensitive to microfractures induced by thermaltreatment.Experimentalresultsshow thatfracture toughness increases with the loading rate but decreases with the temperature.However,when the temperature is below 250°C or above 450°C,the dependence of dynamic fracture toughness on the temperature is different from that on other temperatures, which can be explained by the physical processes at the microscopic level of the rock due to heating.At temperatures below 250°C,the thermal expansion of grains leads to an increase in the toughness of the rock(Yin et al.,2012).At temperatures above 450°C,the sources of weakness such as grain boundaries and phase transition of silicon are depleted,as a result the decrease in fracture toughness is not as signifcant as that in other temperature ranges.

5.6.Dynamic testing method for rocks with water

The water saturation plays a signifcant role in the strengths of rock materials.Many investigations have been performed to determine the strength of rocks under different saturation conditions(Colback and Wild,1965;Burshtein,1969;Hawkins and McConnell,1992).To achieve different levels of saturation in specimens,artifcial wetting of the rock specimens is utilized.For dry rock specimens,they were dried to constant weight in a thermostat at 105°C for at least two days.Air-dried specimens were obtained by prolonging retention in the open air at room temperature.To prepare various degrees of saturated specimens,they were placed in water or in box containing moist sawdust and kept for 2-10 days to increase the moisture content.Rock specimens, which readily swell after absorbing moisture,were kept in sawdust for 2-3 days and then placed in sealed desiccators for 3-4 days to ensure the distribution of moisture throughout the specimen was uniform.The saturation levels were monitored and measured by weighing the specimen.The moisture contents of the specimens can be determined by drying the saturated specimen to constant weight(Burshtein,1969).These results demonstrated that the uniaxial compressive strength of rocks signifcantly decrease from dry to fully saturated condition.Under different loading rates,the water saturation also has an effect on the tensile strength(Han, 2003;Huang et al.,2010b),triaxial strength(Han,2003;Li and Reddish,2004),spalling strength(Lou,1994;Ogata et al.,2004) and point loading strength(Broch,1979).

A number of mechanisms have been proposed to explain the strength reduction with the variation of water saturation,such as pore pressure increase,reduction in friction(Grgic et al.,2005), physical deterioration(Han,2003),chemical interaction with the rock matrix(Ahrens and Rubin,1993),capillary tension decrease (Hawkins and McConnell,1992;Han,2003),and stress corrosion (Hadizadeh and Law,1991).

Huang et al.(2010b)used the BD specimen in the SHPB system to measure the tensile strength of Longyou sandstone with different loading rates and water saturations.The pulse shaping technique was employed to generate a non-dispersive ramp pulse propagating into the incident bar,thus achieving the dynamic force balance.Then,the forces on both ends of the specimen can be calculated by Eq.(1)and the tensile strength of the BD specimen can be obtained by Eq.(10).

Fig.51 shows that the tensile strength for both dryand saturated sandstones increases with loading rate.The saturated sample has stronger rate dependence than the dry sample(the slopes of the linear ftting curves).This difference is caused by the water content since the dry and saturated samples have the same skeleton strength.For concretes,the rate dependence of tensile strength mainly attributes to the viscous cohesive stressσvof free water in the pores(Zheng and Li,2004).

Based on the principle of softening factor,Sf,which was introduced by Jumikis(1983)to describe the water weakening of the compressive strength of rocks,the tensile softening factor,Sft,is defned as

Fig.51.Tensile strength results for dry and saturated Longyou sandstones(after Huang et al.,2010b).

Fig.52.The rate dependence of tensile softening factor of Longyou sandstones(after Huang et al.,2010b).

whereσdtis the tensile strength of the dry rock,andσstis the tensile strength of the saturated rock.

Fig.52 shows the tensile softening factorunder different loading rates.The tensile softening factor is observed to decrease with the loading rate.

6.Conclusions

At high strain rate,the SHPB system is widely used to carry out experimental studies of dynamic properties of rocks.Several loading techniques have been developed for dynamic rock tests using SHPB.First,it is crucial toensure the dynamic force balance in dynamic rock tests.Fordynamic compressive tests,this condition is also called dynamic stress equilibrium and it is recognized as the prerequisite for this material testing method.For other testing methods,this dynamic force balance condition leads to quasi-static stress analysis.Without this condition,a combined experimentalnumerical method has to be used,which is rather tedious in practice and the accuracy is not guaranteed.The pulse shaping technique was proposed to slow down the loading rate and thus to achieve dynamic force balance.Another problem in conventional SHPB tests is that the specimen will be subjected to multiple loading due to the refection of the wave at the impact end of the incident bar.A momentum-trap technique was proposed to ensure single pulse loading and thus enable valid post-mortem analysis of the recovered specimen and assessment of the damage of the samples.Then,since engineering structures are generally under triaxial loading,studies on dynamic tests with multi-axial or confnement loading are important.The multi-axial loading techniques are designed for SHPB tests for rocks.The remaining task is the fne tuning of the design to accommodate the measurements of different rock dynamic properties.

In terms of measurement techniques for SHPB system,noncontact optical methods have been widely utilized to obtain accurate and quantitative data across a wide range of length and time scale.With the advent and development of high-speed photography,the optical techniques discussed in this review have been widely extended to dynamic rock tests at high strain rate.Among these methods(i.e.X-ray micro CT,LLG,DIC,Moiré,caustics,photoelastic coating,dynamic infrared thermography),the DIC technique is a promising way to obtain the high resolution full-feld strain information in high strain rate tests,and X-ray CT and other micro-measurements are also effective reconstruction methods for investigating dynamic damage evolution and dynamic failure of rocks in multi-scale.

Because of the recent advances of SHPB techniques,signifcant progress has been made in the quantifcation of various rock dynamic properties.Methods for measuring dynamic compressive strength,dynamic tensile strength,dynamic fexural(bending) strength,dynamic shear strength,and dynamic fracture toughness are eitherimproved orproposed and validated.Dynamic compression method,dynamic Brazil test,and NSCB method were adopted by the ISRM as suggested methods for dynamic rock compression,tension,and fracture methods,respectively,in 2012 by its Commission on Rock Dynamics(2007-2011).Other methods are good candidates for new suggested methods,and developing dynamic rock testing methods is the main objective of the new ISRM Commission on Rock Dynamics(2011-2015).It is noted that some of these dynamic method share the same sample geometries as their static counterparts and some do not.The choice of different geometries is to facilitate data reduction,sample preparation,and experimentation for the dynamic tests.

In the dynamic compression tests,the length to diameter ratio is not as strict as in conventional tests,owing to the utilization of pulse shaping technique.The length to diameter ratio ranging from 0.5 to 1 is acceptable.In the dynamic tension tests,the dynamic SCB method measures the fexural tensile strength,which is higher than the tensile strength measured by the BD method.This can be explained using the non-local failure theory.Besides,the dynamic punch shear test is suitable for measuring dynamic shear strength of rocks.Moreover,three methods for quantifcation of the dynamic fracture toughness of rocks are mainly discussed.The NSCB method is easy to be applied and suitable for coarse-to intermediategrained rocks.The CCNBD and the CCNSCB methods are applicable to fne-grained rocks.Compared with the CCNBD method,the CCNSCB method is advantageous because only one fracture is involved.The methods for studying the effect of temperature and water saturation are discussed as well.Some typical results are presented.

In summary,the SHPB system can be employed to effectively determine the dynamic properties of rocks.However,dynamic testing methods using SHPB system should be carefully assessed and should satisfy the fundamental assumptions of the measurement methods,including dynamic force balance,valid failure pattern and stress distribution.

Confict of interest

The authors wish to confrm that there are no known conficts of interest associated with this publication and there has been no signifcant fnancial support for this work that could have infuenced its outcome.

Acknowledgments

The authors acknowledge the support by the Natural Sciences and Engineering Research Council of Canada(NSERC)through the Discovery Grant No.72031326.

Ahrens TJ,Rubin AM.Impact-induced tensional failure in rock.Journal of Geophysical Research 1993;98(E1):1185-203.

Albertini C,Montagnani M.Testing techniques based on the split Hopkinson bar. Ispra,Italy:EURATOM;1974.

Alves M,Karagiozova D,Micheli GB,Calle MAG.Limiting the infuence of friction on the split Hopkinson pressure bar tests by using a ring specimen.International Journal of Impact Engineering 2012;49:130-41.

Amiot F,Bornert M,Doumalin P,Dupré JC,Fazzini M,Orteu JJ,Poilâne C,Robert L, Rotinat R,Toussaint E,Wattrisse B,Wienin JS.Assessment of digital image correlation measurement accuracy in the ultimate error regime:main results of a collaborative benchmark.Strain 2013;49(6):483-96.

ASM.High strain rate tension and compression tests.In:Kuhn H,Medlin D,editors. ASM handbook.Mechanical testing and evaluation,vol.8.Ohio,USA:ASM International;2000.p.429-46.

ASTM Standard E399-90.Standard test method for plane strain fracture toughness of metallic materials.In:ASTM ed.Annual book of ASTM standards.West Conshohocken,Pennsylvania,USA:ASTM International;2002.p.413-44.

Avril S,Bonnet M,Bretelle AS,Grédiac M,Hild F,Ienny P,Latourte F,Lemosse D, Pagano S,Pagnacco E,Pierron F.Overview of identifcation methods of mechanical parameters based on full-feld measurements.Experimental Mechanics 2008;48(4):381-402.

Barla G,Zhao J.Special issue:rock dynamics and earthquake engineering.Rock Mechanics and Rock Engineering 2010;43(6):655-960.

Barsoum RS.Triangular quarter-point elements as elastic and perfectly-plastic crack tip elements.International Journal for Numerical Methods in Engineering 1977;11(1):85-98.

Bell JF.An experimental diffraction grating study of the quasi-static hypothesis of the split Hopkinson bar experiment.Journal of the Mechanics and Physics of Solids 1966;14(6):309-27.

Bertholf LD,Karnes CH.Two-dimensional analysis of the split Hopkinson pressure bar system.Journal of the Mechanics and Physics of Solids 1975;23(1):1-19.

Bertram A,Kalthoff JF.Crack propagation toughness of rock for the range of low to very high crack speeds.Key Engineering Materials 2003;251-252:423-30.

Bésuelle P,Viggiani G,Lenoir N,Desrues,Bornert M.X-ray micro CT for studying strain localization in clay rocks under triaxial compression.Advances in X-ray Tomography for Geomaterials 2010;118:35-52.

Bieniawski ZT.Fracture dynamics of rock.International Journal of Fracture Mechanics 1968;4(4):415-30.

Bieniawski ZT,Bernede MJ.Suggested methods for determining the uniaxial compressive strength and deformability of rock materials.International Journal ofRockMechanicsandMiningSciencesandGeomechanicsAbstracts 1979;16(2):138-40.

Bieniawski ZT,Hawkes I.Suggested methods for determining tensile strength of rock materials.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts 1978;15(3):99-103.

Bischoff PH,Perry SH.Compressive behaviour of concrete at high strain rates. Materials and Structures 1991;24(6):425-50.

Böhme W,Kalthoff JF.The behavior of notched bend specimens in impact testing. International Journal of Fracture 1982;20(4):R139-43.

Bornert M,Brémand F,Doumalin P,Dupré JC,Fazzini M,Grédiac M,Hild F,Mistou S, Molimard J,Orteu JJ,Robert L,Surrel Y,Vacher P,Wattrisse B.Assessment of digital image correlation measurement errors:methodology and results. Experimental Mechanics 2009;49(3):353-70.

Broch E.Changes in rock strength by water.In:Proceedings of the 4th international congress on rock mechanics.Rotterdam:A.A.Balkema;1979.p.71-5.

Burshtein LS.Effect of moisture on the strength and deformability of sandstone. Journal of Mining Science 1969;5:573-6.

Cadoni E,Albertini C.Modifed Hopkinson bar technologies applied to the high strain rate rock tests.In:Zhou YX,Zhao J,editors.Advances in rock dynamics and applications.New York,USA:CRC Press;2011.p.79-104.

Cadoni E,Solomos G,Albertini C.Mechanical characterisation of concrete in tension and compression at high strain rate using a modifed Hopkinson bar.Magazine of Concrete Research 2009;61(3):221-30.

Cai M,Kaiser PK,Suorineni F,Su K.A study on the dynamic behavior of the Meuse/ Haute-Marne argillite.Physics and Chemistry of the Earth,Parts A/B/C 2007;32(8-14):907-16.

Carter BJ.Size and stress gradient effects on fracture around cavities.Rock Mechanics and Rock Engineering 1992;25(3):167-86.

Chen W,Ravichandran G.An experimental technique for imposing dynamic multiaxial-compression withmechanicalconfnement.ExperimentalMechanics 1996;36(2):155-8.

Chen W,Ravichandran G.Dynamic compressive failure of a glass ceramic under lateral confnement.Journal of the Mechanics and Physics of Solids 1997;45(8): 1303-28.

Chen W,Ravichandran G.Failure mode transition in ceramics under dynamic multiaxial compression.International Journal of Fracture 2000;101(1-2):141-59.

Chen WW,Song B.Split Hopkinson(Kolsky)bar:design,testing and applications. New York,USA:Springer;2010.

Chen W,Lu F,Cheng M.Tension and compression tests of two polymers under quasi-static and dynamic loading.Polymer Testing 2002;21(2):113-21.

Chen R,Xia K,Dai F,Lu F,Luo SN.Determination of dynamic fracture parameters using a semi-circular bend technique in split Hopkinson pressure bar testing. Engineering Fracture Mechanics 2009;76(9):1268-76.

Chen WW,Hudspeth MC,Claus B,Parab ND,Black JT,Fezzaa K,Luo SN.In situ damage assessment using synchrotron X-rays in materials loaded by a Hopkinson bar.Philosophical Transactions of the Royal Society of London Series A: Mathematical,Physical and Engineering Sciences 2014;372(2015).http:// dx.doi.org/10.1098/rsta.2013.0191.

Christensen RJ,Swanson SR,Brown WS.Split-Hopkinson-bar tests on rock under confning pressure.Experimental Mechanics 1972;12(11):508-13.

Colback PSB,Wild BL.The infuence of moisture content on the compressive strength of rock.In:Proceedings of the 3rd Canadian rock mechanics symposium.Toronto,Canada;1965.p.65-83.

Costin LS.Static and dynamic fracture behaviour of oil shale.In:Freiman SW, Fuller ER,editors.Fracture mechanics for ceramics,rock and concrete,ASTM STP 745.Pennsylvania,USA:American Society for Testing and Materials;1981. p.169-84.

Curran DR,Seaman L,Shockey DA.Dynamic failure of solids.Physics Reports-Review Section of Physics Letters 1987;147(5-6):253-388.

Dabboussi W,Nemes JA.Modeling of ductile fracture using the dynamic punch test. International Journal of Mechanical Sciences 2005;47(8):1282-99.

Dai F,Xia K,Luo SN.Semicircular bend testing with split Hopkinson pressure bar for measuring dynamic tensile strength of brittle solids.Review of Scientifc Instruments 2008;79(12):123903-6.

Dai F,Xia KW,Tang LZ.Rate dependence of the fexural tensile strength of Laurentian granite.International Journal of Rock Mechanics and Mining Sciences 2010a;47(3):469-75.

Dai F,Huang S,Xia K,Tan Z.Some fundamental issues in dynamic compression and tension tests of rocks using split Hopkinson pressure bar.Rock Mechanics and Rock Engineering 2010b;43(6):657-66.

Dai F,Chen R,Iqbal MJ,Xia K.Dynamic cracked chevron notched Brazilian disc method for measuring rock fracture parameters.International Journal of Rock Mechanics and Mining Sciences 2010c;47(4):606-13.

Dai F,Chen R,Xia K.A semi-circular bend technique for determining dynamic fracture toughness.Experimental Mechanics 2010d;50(6):783-91.

Dai F,Xia K,Zheng H,Wang YX.Determination of dynamic rock Mode-I fracture parameters using cracked chevron notched semi-circular bend specimen.Engineering Fracture Mechanics 2011;78(15):2633-44.

Daniel IM,Rowlands RE.On wave and fracture propagation in rock media.Experimental Mechanics 1975;15(12):449-57.

Davies RM.A critical study of the Hopkinson pressure bar.Philosophical Transactions of the Royal Society of London Series A:Mathematical,Physical and Engineering Sciences 1948;240(821):375-457.

Davies EDH,Hunter SC.The dynamic compression testing of solids by the method of the split Hopkinson pressure bar.Journal of the Mechanics and Physics of Solids 1963;11(3):155-79.

Desrues J,Viggiani G,Besuelle P.Advances in X-ray tomography for Geomaterials. Newport Beach,USA:Iste Publishing Company;2006.

Dong S,Wang Y,Xia Y.Stress intensity factors for central cracked circular disk subjected to compression.Engineering Fracture Mechanics 2004;71(7-8): 1135-48.

Dong S,Wang Y,Xia Y.A fnite element analysis for using Brazilian disk in split Hopkinson pressure bar to investigate dynamic fracture behavior of brittle polymer materials.Polymer Testing 2006;25(7):943-52.

Dwivedi RD,Soni AK,Goel RK,Dube AK.Fracture toughness of rocks under sub-zero temperature conditions.International Journal of Rock Mechanics and Mining Sciences 2000;37(8):1267-75.

Ellwood S,Griffths LJ,Parry DJ.Materials testing at high constant strain rates. Journal of Physics E:Scientifc Instruments 1982;15(3):280.

Erzar B,Forquin P.An experimental method to determine the tensile strength of concrete at high rates of strain.Experimental Mechanics 2010;50(7):941-55.

Fang Q,Ruan Z,Zhai C,Jiang X,Chen L,Fang W.Split Hopkinson pressure bar test and numerical analysis of salt rock under confning pressure and temperature. Chinese Journal of Rock Mechanics and Engineering 2012;31(9):1756-65(in Chinese).

Feng XT,Chen SL,Zhou H.Real-time computerized tomography(CT)experiments on sandstone damage evolution during triaxial compression with chemical corrosion.International Journal of Rock Mechanics and Mining Sciences 2004;41(2):181-92.

Field JE,Walley SM,Proud WG,Goldrein HT,Siviour CR.Review of experimental techniques for high rate deformation and shock studies.International Journal of Impact Engineering 2004;30(7):725-75.

Forquin P,Gary G,Gatuingt F.A testing technique for concrete under confnement at high rates of strain.International Journal of Impact Engineering 2008;35(6): 425-46.

Forquin P,Safa K,Gary G.Infuence of free water on the quasi-static and dynamic strength of concrete in confned compression tests.Cement and Concrete Research 2010;40(2):321-33.

Forrestal MJ,Wright TW,Chen W.The effect of radial inertia on brittle samples during the split Hopkinson pressure bar test.International Journal of Impact Engineering 2007;34(3):405-11.

Frantz CE,Follansbee PS,Wright WJ.New experimental techniques with the split Hopkinson pressure bar.In:8th international conference on high energy rate fabrication.San Antonio,Texas,USA;1984.p.17-21.

Frew DJ,Forrestal MJ,Chen W.A split Hopkinson pressure bar technique to determine compressive stress-strain data for rock materials.Experimental Mechanics 2001;41(1):40-6.

Frew DJ,Forrestal MJ,Chen W.Pulse shaping techniques for testing brittle materials with a split Hopkinson pressure bar.Experimental Mechanics 2002;42(1):93-106.

Frew DJ,Akers SA,Chen W,Green ML.Development of a dynamic triaxial Kolsky bar.Measurement Science and Technology 2010;21(10):105704.

Gama BA,Lopatnikov SL,Gillespie JW.Hopkinson bar experimental technique:a critical review.Applied Mechanics Reviews 2004;57(4):223-50.

Gao G,Huang S,Xia K,Li Z.Application of digital image correlation(DIC)in dynamic notched semi-circular bend(NSCB)tests.Experimental Mechanics 2014.http:// dx.doi.org/10.1007/s11340-014-9863-5.

Gary G,Bailly P.Behaviour of quasi-brittle material at high strain rate:experiment and modelling.European Journal of Mechanics-A/Solids 1998;17(3):403-20.

Gerlach R,Sathianathan SK,Siviour C,Petrinic N.A novel method for pulse shaping of split Hopkinson tensile bar signals.International Journal of Impact Engineering 2011;38(12):976-80.

Gilat A.Torsional Kolsky bar testing.In:Kuhn H,Medlin D,editors.ASM handbook. Mechanical testing and evaluation,vol.8.Ohio,USA:ASM International;2000. p.505-15.

Gilat A,Schmidt TE,Walker AL.Full feld strain measurement in compression and tensile split Hopkinson bar experiments.Experimental Mechanics 2009;49(2): 291-302.

Goldsmith W,Sackman JL,Ewerts C.Static and dynamic fracture strength of Barre granite.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts 1976;13(11):303-9.

Gomez JT,Shukla A,Sharma A.Static and dynamic behavior of concrete and granite in tension with damage.Theoreticaland Applied FractureMechanics 2001;36(1):37-49.

Gong JC,Malvern LE.Passively confned tests of axial dynamic compressive strength of concrete.Experimental Mechanics 1990;30(1):55-9.

Gray GT.Classic split-Hopkinson pressure bar testing.In:Kuhn H,Medlin D,editors. ASM handbook.Mechanical testing and evaluation,vol.8.Ohio,USA:ASM International;2000.p.1027-67.

Gray GT,Blumenthal WR.Split-Hopkinson pressure bar testing of soft materials.In: Kuhn H,Medlin D,editors.ASM handbook.Mechanical testing and evaluation, vol.8.Ohio,USA:ASM International;2000.p.1093-114.

Grgic D,Giot R,Homand F,Giraud A.Effect of suction on the mechanical behaviour of iron ore rock.International Journal for Numerical and Analytical Methods in Geomechanics 2005;29(8):789-827.

Hadizadeh J,Law RD.Water-weakening of sandstone and quartzite deformed at various stress and strain rates.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts 1991;28(5):431-9.

Han G.Rock stability under different fuid fow conditions[PhD Thesis].Waterloo, Canada:University of Waterloo;2003.

Harding J,Welsh LM.A tensile testing technique for fbre-reinforced composites at impact rates of strain.Journal of Materials Science 1983;18(6):1810-26.

Harding J,Wood EO,Campbell JD.Tensile testing of materials at impact rates of strain.Journal of Mechanical Engineering Science 1960;2(2):88-96.

Hartley RS,Cloete TJ,Nurick GN.An experimental assessment of friction effects in the split Hopkinson pressure bar using the ring compression test.International Journal of Impact Engineering 2007;34(10):1705-28.

Hauser FE.Techniques for measuring stress-strain relations at high strain rates. Experimental Mechanics 1966;6(8):395-402.

Hawkins AB,McConnell BJ.Sensitivity of sandstone strength and deformability to changes in moisture-content.Quarterly Journal of Engineering Geology and Hydrogeology 1992;25(2):115-30.

Hild F,Roux S.Digital image correlation:from displacement measurement to identifcation of elastic properties-A review.Strain 2006;42(2):69-80.

Hopkinson B.A method of measuring the pressure produced in the detonation of high explosives or by the impact of bullets.Philosophical Transactions of the Royal Society of London Series A:Mathematical,Physical and Engineering Sciences 1914;213(497-508):437-56.

Howe SP,Goldsmith W,Sackman JL.Macroscopic static and dynamic mechanical properties of Yule marble.Experimental Mechanics 1974;14(9):337-46.

Huang S,Chen R,Xia KW.Quantifcation of dynamic tensile parameters of rocks using a modifed Kolsky tension bar apparatus.Journal of Rock Mechanics and Geotechnical Engineering 2010a;2(2):162-8.

Huang S,Xia K,Yan F,Feng X.An experimental study of the rate dependence of tensile strength softening of Longyou sandstone.Rock Mechanics and Rock Engineering 2010b;43(6):677-83.

Huang S,Feng XT,Xia K.A dynamic punch method to quantify the dynamic shear strength of brittle solids.Review of Scientifc Instruments 2011a;82(5):053901.

Huang S,Luo SN,TatoneBSA,Xia K.Dynamicfracture testsofpolymethylmethacrylate using a semicircular bend technique.Journal of Mechanics of Materials and Structures 2011b;6(6):813-26.

Huang S,Xia K,Zheng H.Observation of microscopic damage accumulation in brittle solids subjected to dynamic compressive loading.Review of Scientifc Instruments 2013;84(9):093903.

Hudson JA,Brown ET,Rummel F.The controlled failure of rock discs and rings loaded in diametral compression.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts 1972;9(2):241-8.

Hudspeth M,Claus B,Dubelman S,Black J,Mondal A,Parab N,Funnell C,Hai F, Qi ML,Fezzaa K,Luo SN,Chen W.High speed synchrotron X-ray phase contrast imaging of dynamic material response to split Hopkinson bar loading.Review of Scientifc Instruments 2013;84(2):025102.

Hughes ML,Tedesco JW,Ross CA.Numerical analysis of high strain rate splittingtensile tests.Computers and Structures 1993;47(4-5):653-71.

Iqbal MJ,Mohanty B.Experimental calibration of ISRM suggested fracture toughness measurement techniques in selected brittle rocks.Rock Mechanics and Rock Engineering 2007;40(5):453-75.

Iqbal M,Mohanty B,Xia K.Dynamic tensile strength and mode-I fracture toughness in granitic rocks.In:Proceedings of the 11th international congress and exposition.Orlando,Florida,USA;2008.p.1-8.

International Society for Rock Mechanics(ISRM)Commission on Testing Methods. Suggested method for determining mode I fracture toughness using cracked chevron notched Brazilian disc(CCNBD)specimens.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts 1995;32(1): 57-64.

Jia L,Chen M,Jin Y.3D imaging of fractures in carbonate rocks using X-ray computed tomography technology.Carbonates and Evaporites 2014;29(2): 147-53.

Jiang FC,Vecchio KS.Experimental investigation of dynamic effects in a two-bar/ three-point bend fracture test.Review of Scientifc Instruments 2007;78(6): 063903.

Jiang FC,Vecchio KS.Hopkinson bar loaded fracture experimental technique:a critical review of dynamic fracture toughness tests.Applied Mechanics Reviews 2009;62(6):060802-39.

Jiang FC,Liu RT,Zhang XX,Vecchio KS,Rohatgi A.Evaluation of dynamic fracture toughnessKIdby Hopkinson pressure bar loaded instrumented Charpy impact test.Engineering Fracture Mechanics 2004;71(3):279-87.

Jumikis AR.Rock mechanics.Clausthal,Germany:Trans.Tech.;1983.

Kawakata H,Cho A,Kiyama T,Yanagidani T,Kusunose K,Shimada M.Threedimensional observations of faulting process in Westerly granite under uniaxial and triaxial conditions by X-ray CT scan.Tectonophysics 1999;313(3):293-305.

Kawata K,Hashimoto S,Kurokawa K,Kanayama N.A new testing method for the characterisation of materials in high-velocity tension,mechanical properties at high rates of strain.In:Harding J,editor.Institute of Physics conference series No.47.Oxford,UK:Taylor&Francis Group;1979.p.71-80.

Klepaczko JR,Brara A.An experimental method for dynamic tensile testing of concrete by spalling.International Journal of Impact Engineering 2001;25(4): 387-409.

Klepaczko JR,Bassim MN,Hsu TR.Fracture toughness of coal under quasi-static and impact loading.Engineering Fracture Mechanics 1984;19(2):305-16.

Kolsky H.An investigation of the mechanical properties of materials at very high rates of loading.Proceedings of the Royal Society A:Mathematical,Physical and Engineering Sciences 1949;B62(11):676-700.

Kolsky H.Stress waves in solids.Oxford,UK:Clarendon Press;1953.

Krafft JM,Sullivan AM,Tipper CF.The effect of static and dynamic loading and temperature on the yield stress of iron and mild steel in compression.Proceedings of the Royal Society of London Series A:Mathematical and Physical Sciences 1954;221(1144):114-27.

Kubota S,Ogata Y,Wada Y,Simangunsong G,Shimada H,Matsui K.Estimation of dynamic tensile strength of sandstone.International Journal of Rock Mechanics and Mining Sciences 2008;45(3):397-406.

Kuruppu MD,Obara Y,Ayatollahi MR,Chong KP,Funatsu T.ISRM-suggested method for determining the mode I static fracture toughness using semi-circular bend specimen.Rock Mechanics and Rock Engineering 2014;47(1):267-74.

Lajtai EZ.Effect of tensile stress gradient on brittle fracture initiation.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts 1972;9(5):569-78.

Lambert DE,Ross CA.Strain rate effects on dynamic fracture and strength.International Journal of Impact Engineering 2000;24(10):985-98.

Li QM,Meng H.About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test.International Journal of Solids and Structures 2003;40(2):343-60.

Li Y,Ramesh KT.An optical technique for measurement of material properties in the tension Kolsky bar.International Journal of Impact Engineering 2007;34(4): 784-98.

Li Z,Reddish D.The effect of groundwater recharge on broken rocks.International Journal of Rock Mechanics and Mining Sciences 2004;41(3):280-5.

Li M,Wang R,Han MB.A Kolsky bar:tension,tension-tension.Experimental Mechanics 1993;33(1):7-14.

Li XB,Lok TS,Zhao J,Zhao PJ.Oscillation elimination in the Hopkinson bar apparatus and resultant complete dynamic stress-strain curves for rocks.International Journal of Rock Mechanics and Mining Sciences 2000;37(7):1055-60.

Li ZH,Bi XP,Lambros J,Geubelle PH.Dynamic fber debonding and frictional pushout in model composite systems:experimental observations.Experimental Mechanics 2002;42(4):417-25.

Li XB,Zhou ZL,Lok TS,Hong L,Yin TB.Innovative testing technique of rock subjected to coupled static and dynamic loads.International Journal of Rock Mechanics and Mining Sciences 2008;45(5):739-48.

Li QM,Lu YB,Meng H.Further investigation on the dynamic compressive strength enhancement of concrete-like materials based on split Hopkinson pressure bar tests.Part II:numerical simulations.International Journal of Impact Engineering 2009;36(12):1335-45.

Li XB,Yin TB,Zhou ZL,Hong L,Gao K.Study of dynamic properties of siltstone under coupling effects of temperature and pressure.Chinese Journal of Rock Mechanics and Engineering 2010;29(12):2377-84(in Chinese).

Lim IL,Johnston IW,Choi SK,Boland JN.Fracture testing of a soft rock with semicircular specimens under three-point bending.Part 1-mode I.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts 1994;31(3):185-97.

Lindholm U.Some experiments with the split hopkinson pressure bar.Journal of the Mechanics and Physics of Solids 1964;12(5):317-35.

Lindholm US.High strain rate tests.In:Bunshah RF,editor.Techniques of metals research.Measurement of mechanical properties,vol.5.New York,USA:Wiley Interscience;1971.p.199-271.

Lindholm US,Yeakley LM.High strain-rate testing:tension and compression

. Experimental Mechanics 1968;8(1):1-9.

Lindholm US,Yeakley LM,Nagy A.The dynamic strength and fracture properties of Dresser basalt.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts 1974;11(5):181-91.

Lipkin J,Grady DE,Campbell JD.Dynamic fow and fracture of rock in pure shear.In: The 18th US symposium on rock mechanics(USRMS).USA:Keystone;1977. p.77-80.

Lipkin J,Schuler KW,Parry T.Dynamic torsional failure of limestone tubes.In:The 2nd conference on mechanical properties of material at high rates of strain.UK: Oxford;1979.p.101-10.

Liu S,Xu J.Study on dynamic characteristics of marble under impact loading and high temperature.International Journal of Rock Mechanics and Mining Sciences 2013;62:51-8.

Lou W.Dynamic fracture behaviour of dry and waterlogged granites.Explosion and Shock Waves 1994;14(3):249-54.

Lu YB,Li QM,Ma GW.Numerical investigation of the dynamic compressive strength of rocks based on split Hopkinson pressure bar tests.International Journal of Rock Mechanics and Mining Sciences 2010;47(5):829-38.

Luo SN,Jensen BJ,Hooks DE,Fezzaa K,Ramos KJ,Yeager JD,Kwiatkowski K, Shimada T.Gas gun shock experiments with single-pulse X-ray phase contrast imaging and diffraction at the advanced photon source.Review of Scientifc Instruments 2012;83(7):073903.

Malinowski JZ,Klepaczko JR.A unifed analytic and numerical approach to specimen behavior in the split Hopkinson pressure bar.International Journal of Mechanical Sciences 1986;28(6):381-91.

Malvar LJ,Ross CA.Review of strain rate effects for concrete in tension.ACI Materials Journal 1998;95(6):735-9.

Malvern LE,Jenkinds DA,Tang T,McLure S.Dynamic testing of laterally confned concrete.In:Micromechanics of failure of quasi brittle materials.Amsterdam, Netherlands:Elsevier Applied Science;1991.p.343-52.

MatsushimaT,UesugiK,Nakano T,TsuchiyamaA.Visualizationofgrain motion inside a triaxial specimen by micro X-ray CT at SPring-8.Advances in X-ray Tomography for Geomaterials 2006. http://dx.doi.org/10.1002/ 9780470612187.ch24.

Mees F,Swennen R,Van Geet M,Jacobs P.Applications of X-ray computed tomography in the geosciences,215.London:Geological Society;2003.Special Publications,(1):1-6.

Meng H,Li QM.Correlation between the accuracy of a SHPB test and the stress uniformity based on numerical experiments.International Journal of Impact Engineering 2003;28(5):537-55.

Mohr D,Gary G,Lundberg B.Evaluation of stress-strain curve estimates in dynamic experiments.International Journal of Impact Engineering 2010;37(2):161-9.

Nakano M,Kishida K,Yamauchi Y,Sogabe Y.Dynamic fracture initiation in brittle materialsundercombined mode I/IIloading.JournaldePhysiqueIV 1994;04(C8).C8-C695-C8-C700.

Narayanasamy R,Pandey KS.Phenomenon of barrelling in aluminium solid cylinders during cold upset-forming.Journal of Materials Processing Technology 1997;70(1-3):17-21.

Nemat-Nasser S.Introduction to high strain rate testing.In:Kuhn H,Medlin D, editors.ASM handbook.Mechanical testing and evaluation,vol.8.Ohio,USA: ASM International;2000.p.427-8.

Nemat-Nasser S,Isaacs JB,Starrett JE.Hopkinson techniques for dynamic recovery experiments.Proceedings of the Royal Society of London Series A:Mathematical and Physical Sciences 1991;435(1894):371-91.

Nicholas T.Tensile testing of materials at high rates of strain.Experimental Mechanics 1981;21(5):177-85.

Nie X,Song B,Ge Y,Chen W,Weerasooriya T.Dynamic tensile testing of soft materials.Experimental Mechanics 2009;49(4):451-8.

Ogata Y,Jung W,Kubota S,Wada Y.Effect of the strain rate and water saturation for the dynamic tensile strength of rocks.In:Itoh S,Hokamoto K,Fujita M,editors. Materials science forum,vols.465-466.Switzerland:Trans.Tech.Publications Inc;2004.p.361-6.

Ogawa K.Impact-tension compression test by using a split-Hopkinson bar.Experimental Mechanics 1984;24(2):81-6.

Otani J,Obara Y.X-ray CT for geomaterials:soils,concrete,rocks.Lisse,Netherlands: Swets&Zeitlinger;2004.

Ouchterlony F.Suggested methods for determining the fracture toughness of rock. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts 1988;25(2):71-96.

Owen DM,Zhuang S,Rosakis AJ,Ravichandran G.Experimental determination of dynamic crack initiation and propagation fracture toughness in thin aluminum sheets.International Journal of Fracture 1998;90(1-2):153-74.

Paliwal B,Ramesh KT,McCauley JW,Chen M.Dynamic compressive failure of AlON under controlled planar confnement.Journal of the American Ceramic Society 2008;91(11):3619-29.

Pan B,Qian K,Xie H,Asundi A.Two-dimensional digital image correlation for inplane displacement and strain measurement:a review.Measurement Science and Technology 2009;20(6):062001.http://dx.doi.org/10.1088/0957-0233/20/6/ 062001.

Parab ND,Claus B,Hudspeth MC,Black JT,Mondal A,Sun J,Fezzaa K,Xiao X, Luo SN,Chen W.Experimental assessment of fracture of individual sand particles at different loading rates.International Journal of Impact Engineering 2014;68:8-14.

Paterson MS,Wong TF.Experimental rock deformation:the brittle feld.2nd ed. Berlin Heidelberg,Germany:Springer-Verlag;2005.

Peirs J,Verleysen P,Van Paepegem W,Degrieck J.Determining the stress-strain behaviour at large strains from high strain rate tensile and shear experiments.International Journal of Impact Engineering 2011;38(5):406-15.

Perkins RD,Green SJ,Friedman M.Uniaxial stress behavior of porphyritic tonalite at strain rates to 103/second.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts 1970;7(5):527-35.

Pierron F,Forquin P.Ultra-high-speed full-feld deformation measurements on concrete spalling specimens and stiffness identifcation with the virtual felds method.Strain 2012;48(5):388-405.

Qu JB,Dabboussi W,Hassani F,Nemes J,Yue S.Effect of microstructure on static and dynamic mechanical property of a dual phase steel studied by shear punch testing.ISIJ International 2005;45(11):1741-6.

Ramesh KT.High rates and impact experiments.In:Sharpe WN,editor.Springer handbook of experimental solid mechanics.New York,USA:Springer;2008. p.929-60.

Ramesh KT,Narasimhan S.Finite deformations and the dynamic measurement of radial strains in compression Kolsky bar experiments.International Journal of Solids and Structures 1996;33(25):3723-38.

Rastogi PK,Hack E.Optical methods for solid mechanics:a full-feld approach.New York,USA:John Wiley&Sons;2012.

Ravi-Chandar K.Dynamic fracture.London,UK:Elsevier Science;2004.

Ravichandran G,Subhash G.Critical appraisal of limiting strain rates for compression testing of ceramics in a split Hopkinson pressure bar.Journal of the American Ceramic Society 1994;77(1):263-7.

Raynaud S,Fabre D,Mazerolle F,Geraud Y,Latiere HJ.Analysis of the internal structure of rocks and characterization of mechanical deformation by a nondestructive method:X-ray tomodensitometry.Tectonophysics 1989;159(1-2): 149-59.

Renter JA.Applications of computerized tomography in sedimentology.Marine Georesources&Geotechnology 1989;8(3):201-11.

Rittel D,Lee S,Ravichandran G.A shear-compression specimen for large strain testing.Experimental Mechanics 2002;42(1):58-64.

Rome J,Isaacs J,Nemat-Nasser S.Hopkinson techniques for dynamic triaxial compression tests.In:Gdoutos E,editor.Recent advances in experimental mechanics.Netherlands:Springer;2004.p.3-12.

Ross CA,Thompson PY,Tedesco JW.Split-Hopkinson pressure-bar tests on concrete and mortarin tension and compression.ACIMaterialsJournal 1989;86(5):475-81.

Ross CA,Tedesco JW,Kuennen ST.Effects of strain-rate on concrete strength.ACI Materials Journal 1995;92(1):37-47.

Schey JA,Venner TR,Takomana SL.The effect of friction on pressure in upsetting at low diameter-to-height ratios.Journal of Mechanical Working Technology 1982;6(1):23-33.

Schuler H,Mayrhofer C,Thoma K.Spall experiments for the measurement of the tensile strength and fracture energy of concrete at high strain rates.International Journal of Impact Engineering 2006;32(10):1635-50.

Shan R,Jiang Y,Li B.Obtaining dynamic complete stress-strain curves for rock using the split Hopkinson pressure bar technique.International Journal of Rock Mechanics and Mining Sciences 2000;37(6):983-92.

Shewmon PG,Zackay VF.Response of metals to high velocity deformation.New York,USA:Interscience Publishers Inc.;1961.

Shi W,Wu Y,Wu L.Quantitative analysis of the projectile impact on rock using infrared thermography.International Journal of Impact Engineering 2007;34(5):990-1002.

Siviour CR,Grantham SG.High resolution optical measurements of specimen deformation in the split Hopkinson pressure bar.The Imaging Science Journal 2009;57(6):333-43.

Siviour CR,Arthington MR,Wielewski E,Petrinic N.Increasing data from high rate characterization experiments using optical reconstruction.APS Shock Compression of Condensed Matter Meeting Abstracts 2011;1426(1):438-41.

Song B,Chen W.Loading and unloading split Hopkinson pressure bar pulse-shaping techniques for dynamic hysteretic loops.Experimental Mechanics 2004;44(6): 622-7.

Song B,Chen W.Energy for specimen deformation in a split Hopkinson pressure bar experiment.Experimental Mechanics 2006;46(3):407-10.

Staab GH,Gilat A.A direct-tension split Hopkinson bar for high strain-rate testing. Experimental Mechanics 1991;31(3):232-5.

Subhash G,Ravichandran G,Gray GT.Split-Hopkinson pressure bar testing of ceramics.In:Kuhn H,Medlin D,editors.ASM handbook.Mechanical testing and evaluation,vol.8.Ohio,USA:ASM International;2000.p.1114-34.

Sutton MA,Orteu JJ,Schreier H.Image correlation for shape,motion and deformation measurements:basic concepts,theory and applications.New York,USA: Springer;2009.

Tang C,Xu X.A new method for measuring dynamic fracture-toughness of rock. Engineering Fracture Mechanics 1990;35(4-5):783-91.

Tedesco JW,Ross CA,Brunair RM.Numerical analysis of dynamic split cylinder tests. Computers&Structures 1989;32(3-4):609-24.

Toutlemonde F,Gary G.Dynamic behavior of concrete:experimental aspects.In: Mazars J,Millard A,editors.Dynamic behavior of concrete and seismic engineering.Washington D.C.,USA:Wiley-ISTE;2009.p.1-54.

Van de Steen B,Vervoort A.Non-local stress approach to fracture initiation in laboratory experiments with a tensile stress gradient.Mechanics of Materials 2001;33(12):729-40.

Van Geet M,Swennen R,Wevers M.Quantitative analysis of reservoir rocks by microfocus X-ray computerised tomography. Sedimentary Geology 2000;132(1-2):25-36.

Viggiani G,Lenoir N,Bésuelle P,Di Michiel M,Marello S,Desrues J,Kretzschmer M. X-ray microtomography for studying localized deformation in fne-grained geomaterials under triaxialcompression.ComptesRendus Mécanique 2004;332(10):819-26.

Vinegar HJ.X-ray CT and NMR imaging of rocks.Journal of Petroleum Technology 1986;38(3):257-9.

Vinegar HJ,De Waal JA,Wellington SL.CT studies of brittle failure in Castlegate sandstone.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts 1991;28(5):441-50.

Walley SM.Historical review of high strain rate and shock properties of ceramics relevant to their application in armour.Advances in Applied Ceramics 2010;109(8):446-66.

Wang QZ,Li W,Song XL.A method for testing dynamic tensile strength and elastic modulusofrockmaterialsusingSHPB.PureandApplied Geophysics 2006;163(5-6):1091-100.

Wang QZ,Li W,Xie HP.Dynamic split tensile test of fattened Brazilian disc of rock with SHPB setup.Mechanics of Materials 2009;41(3):252-60.

Wang QZ,Zhang S,Xie HP.Rock dynamic fracture toughness tested with holedcracked fattened Brazilian discs diametrically impacted by SHPB and its size effect.Experimental Mechanics 2010;50(7):877-85.

Wang QZ,Feng F,Ni M,Gou XP.Measurement of mode I and mode II rock dynamic fracture toughness with cracked straight through fattened Brazilian disc impacted by split Hopkinson pressure bar.Engineering Fracture Mechanics 2011a;78(12):2455-69.

Wang S,Zhang MH,Quek ST.Effect of specimen size on static strength and dynamic increase factor of high-strength concrete from SHPB test.Journal of Testing and Evaluation 2011b;39(5).http://dx.doi.org/10.1520/JTE103370.

Weerasooriya T,Moy P,Casem D,Cheng M,Chen W.A four-point bend technique to determine dynamic fracture toughness of ceramics.Journal of the American Ceramic Society 2006;89(3):990-5.

Wu H,Zhang Q,Huang F,Jin Q.Experimental and numerical investigation on the dynamic tensile strength of concrete.International Journal of Impact Engineering 2005;32(1-4):605-17.

Xia K.Status of characterization of strength and fracture properties of rocks under dynamic loading.In:Singh PK,Sinha A,editors.Rock fragmentation by blasting: proceedings of the 10th international symposium on rock fragmentation by blasting.CRC Press;2012.p.41-51.

Xia K,Chalivendra VB,Rosakis AJ.Observing ideal“self-similar”crack growth in experiments.Engineering Fracture Mechanics 2006;73(18):2748-55.

Xia K,Nasseri MHB,Mohanty B,Lu F,Chen R,Luo SN.Effects of microstructures on dynamic compression of barre granite.International Journal of Rock Mechanics and Mining Sciences 2008;45(6):879-87.

Xia K,Dai F,Chen R.Advancements in Hopkinson pressure bar techniques and applications to rock strength and fracture.In:Zhou Y,Zhao J,editors.Advances in rock dynamics and applications.Boca Raton,Florida,USA:CRC Press/A.A. Balkema;2011.p.35-78.

Yang RS,Yue ZW,Sun ZH,Xiao TS,Guo DM.Dynamic fracture behavior of rock under impact load using the caustics method.Mining Science and Technology (China)2009;19(1):79-83.

Yin TB,Li XB,Xia K,Huang S.Effect of thermal treatment on the dynamic fracture toughness of Laurentian granite.Rock Mechanics and Rock Engineering 2012;45(6):1087-94.

Yu Y,Zhang ZX.Determining critical time of rock dynamic fracture by dynamic Moire method.Journal of University of Science and Technology Beijing 1995;2(2):109-13.

Yu Y,Zhang JX,Zhang JC.A modifed Brazilian disk tension test.International Journal of Rock Mechanics and Mining Sciences 2009;46(2):421-5.

Yuan F,Prakash V,Tullis T.Origin of pulverized rocks during earthquake fault rupture.Journal of GeophysicalResearch: Solid Earth (1978-2012) 2011;116(B6).http://dx.doi.org/10.1029/2010JB007721.

Yun TS,Jeong YJ,Kim KY,Min KB.Evaluation of rock anisotropy using 3D X-ray computed tomography.Engineering Geology 2013;163:11-9.

Zhang QB,Zhao J.Determination of mechanical properties and full-feld strain measurements of rock material under dynamic loads.International Journal of Rock Mechanics and Mining Sciences 2013a;60:423-39.

Zhang QB,Zhao J.Effect of loading rate on fracture toughness and failure micromechanisms in marble.Engineering Fracture Mechanics 2013b;102:288-309.

Zhang QB,Zhao J.A review of dynamic experimental techniques and mechanical behaviour of rock materials.Rock Mechanics and Rock Engineering 2014;47(4): 1411-78.

Zhang ZX,Kou SQ,Yu J,Yu Y,Jiang LG,Lindqvist PA.Effects of loading rate on rock fracture.InternationalJournalofRockMechanicsand MiningSciences 1999;36(5):597-611.

Zhang ZX,Kou SQ,Jiang LG,Lindqvist PA.Effects of loading rate on rock fracture: fracture characteristics and energy partitioning.International Journal of Rock Mechanics and Mining Sciences 2000;37(5):745-62.

Zhang ZX,Yu J,Kou SQ,Lindqvist PA.Effects of high temperatures on dynamic rock fracture.InternationalJournalofRockMechanicsand Mining Sciences 2001;38(2):211-25.

Zhang M,Wu HJ,Li QM,Huang FL.Further investigation on the dynamic compressive strength enhancement of concrete-like materials based on split Hopkinson pressure bar tests.Part I:experiments.International Journal of Impact Engineering 2009;36(12):1327-34.

Zhao J.An overview of some recent progress in rock dynamics research.In: Zhou YX,Zhao J,editors.Advances in rock dynamics and applications.Boca Raton,Florida,USA:CRC Press/A.A.Balkema;2011.p.5-33.

Zhao H,Gary G.On the use of SHPB techniques to determine the dynamic behavior of materials in the range of small strains.International Journal of Solids and Structures 1996;33(23):3363-75.

Zhao J,Li HB.Experimental determination of dynamic tensile properties of a granite.InternationalJournalofRock Mechanicsand Mining Sciences 2000;37(5):861-6.

Zhao J,Li HB,Zhao YH.Dynamics strength tests of the Bukit Timah granite. Geotechnical Research Report NTU/GT/98-2.Singapore:Nanyang Technological University;1998.

Zhao J,Zhou YX,Hefny AM,Cai JG,Chen SG,Li HB,Liu JF,Jain M,Foo ST,Seah CC. Rock dynamics research related to cavern development for ammunition storage.Tunnelling and Underground Space Technology 1999;14(4):513-26.

Zhao J,Zhou YX,Xia KW.Advances in rock dynamics modelling,testing and engineering.In:The 12th ISRM international congress on rock mechanics.Beijing, China;2012.p.147-54.

Zheng D,Li QB.An explanation for rate effect of concrete strength based on fracture toughness including free water viscosity.Engineering Fracture Mechanics 2004;71(16-17):2319-27.

Zhou YX,Xia K,Li XB,Li HB,Ma GW,Zhao J,Zhou ZL,Dai F.Suggested methods for determining the dynamic strength parameters and mode-I fracture toughness of rock materials.International Journal of Rock Mechanics and Mining Sciences 2012;49:105-12.

Zhou ZL,Zou Y,Li XB,Jiang YH.Stress evolution and failure process of Brazilian disc under impact.Journal of Central South University 2013;20(1):172-7.

Zhu WC,Tang CA.Numerical simulation of Brazilian disk rock failure under static and dynamic loading.International Journal of Rock Mechanics and Mining Sciences 2006;43(2):236-52.

Dr.Kaiwen Xia is currently an associate professor at the Department of Civil Engineering of the University of Toronto.He obtained both his B.S.and M.S.degrees from the University of Science and Technology of China in 1994 and 1998,majored in Explosion Mechanics.Dr.Xia fnished his Ph.D.degree at the California Institute of Technology in 2005,with major in Mechanical Engineering and minor in Geophysics.After a year working as a postdoctoral research fellow at the Brown University,he joined the University of Toronto in 2006 as an assistant professor and was promoted and granted the tenure in 2012.Dr.Xia’s research is focused on dynamic response of materials and dynamic fractures.His academic contributions include the discovery of supershear earthquakes in the laboratory, systematic study of spontaneous fractures and the development of a series of dynamic testing methods for rocks. He was the key member in the Commission on Rock Dynamics of the International Society for Rock Mechanics (ISRM-CRD)from 2007 to 2011,and championed the drafting of the frst three dynamic testing methods of rocks.He is currently the chair of ISRM-CRD from 2011 to 2015,leading a group of international experts on rock dynamics to develop more ISRM suggested methods for characterizing dynamic rock properties.To date,Dr.Xia has published 40 SCI journal papers,3 book chapters,and numerous conference abstracts and other papers.Among these publications,two frst-authored papers on supershear earthquakes were published onScience.

*Corresponding author.Tel.:+1 4169785942;fax:+1 4169786813.

E-mail address:kaiwen.xia@utoronto.ca(K.Xia).

Peer review under responsibility of Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.

1674-7755©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

http://dx.doi.org/10.1016/j.jrmge.2014.07.008

Split Hopkinson pressure bar(SHPB) Dynamic tests

Rock dynamic properties

Loading rate