Some modifcations to the process of discontinuous deformation analysis

Full length article

Some modifcations to the process of discontinuous deformation analysis

Yong Yua,*,Jianmin Yinb

aSchool of Mechanics and Engineering,Southwest Jiaotong University,Chengdu,Sichuan 610031,China

bYangtze River Scientifc Research Institute,Wuhan,Hubei 430010,China

A R T 1 C L E 1 N F O

Article history:

Received 19 June 2014

Received in revised form

1 December 2014

Accepted 2 December 2014

Available online 24 December 2014

Discontinuous deformation analysis(DDA) Open-close iteration

Contact force

Vertex-vertex contact

Angle bisector

Augmented Lagrangian method(ALM)

This paper presents a modifed method of discontinuous deformation analysis(DDA).In the presented method,open-close iteration may not be needed,small penetration is permitted among blocks,and springs are added between contacting block pairs only when a penetration takes place.The three contact patterns(i.e.sliding,locking and opening)in original DDA method are not involved,and the recognition of these contact patterns and treatment of transformation among patterns are not required either, signifcantly saving the computing time.In a convex to concave contact,there are two candidate entrance edges which may cause uncertainty.In this case,we propose the angle bisector criterion to determine the entrance edge.The spring stiffness is much larger than Young’s modulus in the original DDA,however we fnd that the correct results can still be obtained when it is much smaller than Young’s modulus.Finally, the penetrations by using penalty method and augmented Lagrangian method are compared.Penetration of the latter is 1/4 of the former.The range of spring stiffness for the latter is wider than the former, being 0.01-1 of the former.Both methods can lead to correct contact forces.

©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

1.Introduction

Discontinuous deformation analysis(DDA)pioneered by Shi (1988)is a numerical method which is parallel to continuumbased analysis methods,such as fnite element method(FEM), boundary element method(BEM).It has been the research focus in investigating the kinematics of blocky rock masses since its establishment in 1988.During the past two decades,great achievements have been made on DDA developments,and many efforts have been carried out to validate and improve its performance(MacLaughlin and Doolin,2006).Among them,the drawback of block expanding due to rigid body rotation has been overcome(Ke,1995;MacLaughlin and Sitar,1996;Cheng and Zhang,2000);higher order displacement function was proposed to consider the variable strain of blocks(Koo et al.,1995;Hsiung, 2001;Wang et al.,2007);contacts between blocks have been modeled by using an augmented Lagrangian method(ALM)instead of the penalty method originally proposed by Shi(Lin et al.,1996; Ning et al.,2009);an alternative scheme for the corner-corner contact was suggested(Bao and Zhao,2010,2012);and signifcant developments have been achieved in the research of threedimensional(3D)DDA(Yeung et al.,2007;Beyabanaki et al., 2008,2009;Keneti et al.,2008;Liu et al.,2009;Wu,2010).

The open-close iteration is an important step and also a diffculty in DDA.The original DDA method conducts 5 iterations at each time step,which means that the global equations will be solved for 5 times within one time step.So the computation workload is much heavy.Moreover,there is few reports illustrating the detailed process of open-close iteration.

Bao and Zhao(2010)showed that the contact reference edges in the corner-corner contact are not unique,and it may lead to an indeterminate state in the numerical analysis.In this case,the original DDA method cannot correctly simulate the process of block movement.The approach proposed by Bao and Zhao(2010,2012) to deal with this issue is to add a spring between the moving corner and target corner,then to remove the spring after the frst open-close iteration.

In the original DDA method,the contact situations are classifed into three patterns,i.e.opening,sliding and locking,and relevant operations are needed for the transformation among the patterns. Moreover,the penalty number is always much greater than the Young’s modulus.

A modifed method of DDA is proposed in this study.It can improve the classic DDA in the following aspects:(i)open-close iteration could be omitted and correct results can still be achieved,meaning that the computing speed can be improved;(ii)indetermination in corner-corner contact is solved with a simplifed approach;(iii)there is no need to distinguish the three contact patterns and the transformations among them,therefore such modifed method can be much simplifed and computation can be speeded up;and(iv)stiffness in penalty method and ALM can be less than the Young’s modulus while correct contact force can still be obtained.

2.Modifcation to DDA simulation process

In the original DDA method,the formulae of the complete frst order approximation are adopted to calculate block displacements (u,v)at any point(x,y).When the rotation angle accumulates,block volume will expand.To solve this problem,precise formulae of the displacement for rotation should be adopted.Followed by Ke (1995),the rotation angle is replaced with the sine of rotation angle in the displacement variables of blocki.Accordingly,the displacement matrixTiis changed,and the stiffness and force terms in the global equations due to line load and inertia force should take the modifed forms.Detailed information can be found in Ke(1995).

Blocks are not allowed to penetrate each other in the original DDA theory.Therefore,normal and shear springs are added in block system.This process is called penalty method.To ensure no penetration and no tensile force existing among blocks,open-close iteration must be carried out within every time step.However, the penetration among blocks could not be zero no matter how high the stiffness of spring is.In fact,the contact forces between two adjacent blocks are provided by springs in penalty method.If the contact forces are not zero,the penetration could not be zero either.So,if small penetrations are permitted to exist among blocks,no open-close iteration is needed in DDA simulation.

In the original DDA process,contact patterns between adjacent blocks,such as opening,sliding and locking,should be recognized and recorded at each time step so that springs can be added to or removed from these blocks.In the modifed method,contact detection among block system is performed at every time step,so the recognition of contact patterns will not be necessary.This will make the DDA process simpler and time-saving.

The modifed DDA process can be summarized as the following steps:

(1)Input block geometry data,including each vertex’s sequence number and coordinate,each block’s sequence number,and then draw the graphics of blocks.

(2)Input physico-mechanicalproperties,such as Young’s modulus,Poisson’s ratio,density,friction angle,cohesion of joint material,and initial velocity.

(3)Input parameters for computing control,including length of time step,total simulation time,maximum displacement in one step,critical distance for separating vertex-vertex(V-V) contact and vertex-edge(V-E)contact,stiffness of normal and tangential springs.

(4)Set coeffcient matrix K and matrix of free terms F in global equation to zero.

(5)Treat the fxed displacements in block system(generally zero, i.e.fxed points).

(6)Add body force-induced sub-matrices to global equations.

(7)Add elastic sub-matrices to global equations.

(8)Add inertia force-induced sub-matrices to global equations.

(9)Add other sub-matrices.

(10)Detect contacts among block system,and fnd the invading vertices and entrance edges.Only add normal and tangential springs or friction sub-matrices to global equations while invading takes place.

(11)Solve the global equations KD=F,whereDis the block displacement.

(12)Calculate the displacement of vertices according to block displacementD.

(13)Update block coordinates,and draw blocks’geometry.

(14)Accumulate the time of simulation.

(15)Reduce the time interval for next time step if the maximum displacement in current time step is reached.

(16)Go to step 4 if the accumulated time is less than total simulation time.

(17)The end of program.

Block initial coordinates can be acquired by the following way: number all the vertices in the block system,and save all the coordinates of the vertices in a matrix;then input each block’s sequence number in counter-clockwise;in the end,fnd out each block’s vertex coordinates.

Fig.1 shows an example without iteration,in which a block is sliding from rest along an incline.The block and incline are two right-angled isosceles triangles with edge lengths being 3 m and 10 m,respectively.Two vertices at the bottom of incline are fxed. The material properties for both blocks are as follows:Young’s modulusE=50 GPa,Poisson’s ratioν=0.2,mass density for unit thicknessM=2.7×103kg/m2,acceleration of gravityg=9.8 m/s2. Simulation parameters are as follows:time intervaldt=0.001 s, spring stiffness(penalty number)p=1 GPa(notep＜E),total time for simulationtotaltime=1 s,maximum displacement in a time stepstep_limit=0.01 m,the critical distance for separating V-V contact and V-E contactcritdis=0.005 m.

When the friction angleφis less than 45°,the analytical solutions of displacementsuandvinxandydirections are as follows:

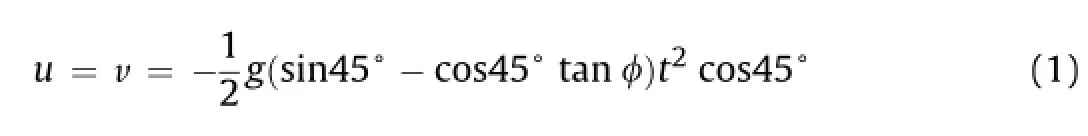
wheretis the sliding time.

Displacementsuandvof pointAin sliding block forφ=0°-45°andt=1 s are calculated and compared with analytical solutions, as shown in Table 1.It can be seen that the relative error is 0.06%-0.66%.

3.Open-close iteration and contact stiffness determination

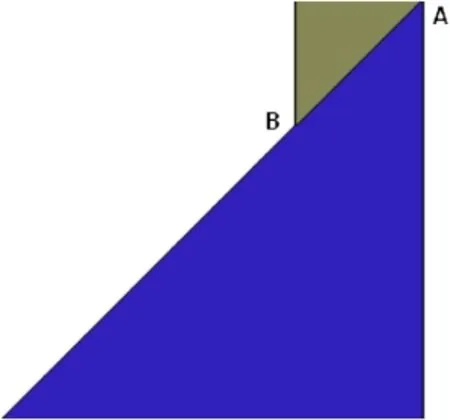
Fig.1.Single block on an incline.

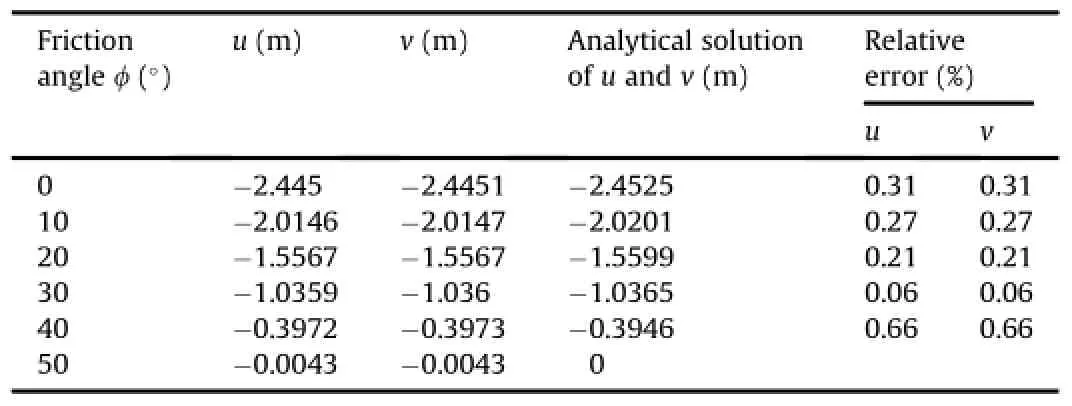
Table 1Displacements of pointAin Fig.1 versus friction angle without open-close iteration.

In some condition,open-close iterations may be needed.In that case,a loop from step 10 to step 12 described in Section 2 is necessary.The number of loop is the number of iteration.Openclose iteration is a diffcult issue in DDA,and no details are given in DDA theory.

We succeeded in conducting open-close iterations by the following procedure:

(1)Before iteration,all sub-matrices except the ones derived from normal and tangential springs should be added to the global equations.Supposing the coeffcient matrix and matrix of free terms in global equations are K0and F0,respectively,we can compute block displacement,update block coordinates,and mark blocks’new positions as position 0.

(2)Detect penetration among blocks for blocks at position 0.If any penetration occurs,add normal and tangential springs(or friction)sub-matrices to the global equations.Supposing the coeffcient matrix is K1,and the matrix of free terms is F1,solve the displacements of block,then update blocks’position,and mark it as position 1.Now,the frst iteration is fnished.

(3)For the second iteration,detect penetration among blocks at position 1,and add spring sub-matrices to K0and F0(if add spring sub-matrices to K1and F1,it would mean that the matrices derived from volume force,inertia force,etc.will be exerted more than one time,which is obviously wrong.After that,repeat this process,and add spring sub-matrices to K0and F0in each iteration.In original DDA code,there are 5 iterations in one time step.

In the original DDA theory,the spring stiffnesspis 10-100 times of Young’s modulus.However,we found that the value of spring stiffness as 1/50 of the Young’s modulus can also obtain the correct simulation result if Young’s moduli of all blocks are the same,the number of blocks is small,and the size of block is in the same magnitude,as shown in Fig.1.This is due to the global equations in this case which do not appear abnormal.For the example in Fig.1, as long as the spring stiffnesspis not too large or too small compared with block Young’s modulus,there is no difference between the results of 1 iteration and 6 iterations.Both of them are very close to theoretical solutions(0.7352 m).The relative error is less than 0.5%(Table 2).

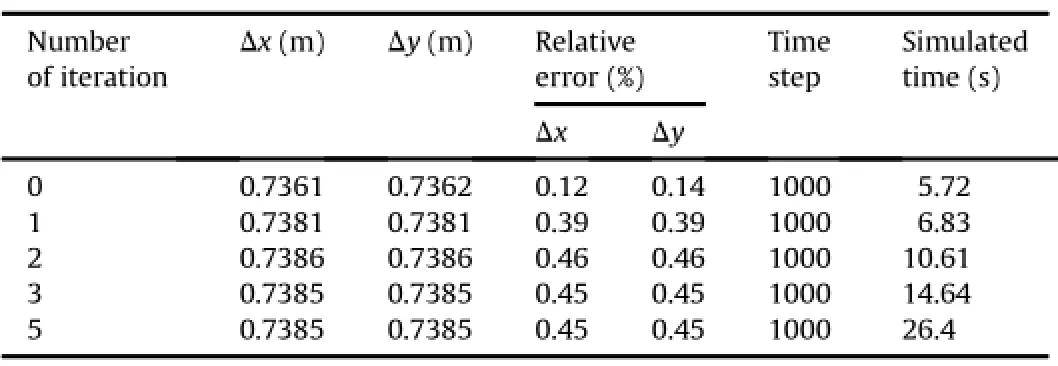
Table 2Displacements of pointAin Fig.1 versus iteration(φ=35°).

4.Procedure of contact detection

The contact of blocks in DDA is divided into two categories,i.e. V-V contact and V-E contact.The aim of contact detection is to fnd out all these two contacts,and to determine the invading vertices and the entrance edges.

A certain pair of invading vertex and entrance edge may belong to V-V contact or V-E contact.The original DDA theory fails to distinguish it.In this modifed method,these two categories of contacts are defned according to the following criterion:(i)if the distance between vertices of any two blocks is less than a critical valuecritdisand the two blocks penetrate each other,then the V-V contact occurs;(ii)if the block vertex invades into another block and the distance between the invading vertex and the nearest vertex in the invaded block is greater than critical distancecritdis, the V-E contact occurs.

For both V-V contact and V-E contact,only when the penetration takes place,we can add normal and tangential springs between the invading vertices and entrance edges,i.e.adding the spring sub-matrices to K and F.If the tangential force is larger than the friction,add the friction matrix only to the matrix F.

Once the invading vertices in V-E contact are determined,the entrance edges must be found out.Usually,the shortest distance method is adopted to determine the entrance edge,i.e.the edge of the invaded block with nearest distance to the invading vertex is the entrance edge.However,only when the displacement is small, the shortest distance criterion can lead to reasonable results.

In DDA simulation,one may encounter such a situation:for the same contact problem,it can be taken as either V-V contact or V-E contactandtheentranceedgemaynotbethesameone.Asshownin Fig.2,verticesAandBpenetrate each other.If it is taken as V-E contact,the entrance edge isBFaccording to the shortest distance criterion.But thisisnottrue,becausetheentranceedgeshouldbeBEandAD.The solution to this probleminBaoandZhao(2012)is to use the trajectory of the vertexAto fnd the entrance edge when the movingvertexinvadesintothetargetblock.However,thismethodis feasible only when vertexAin previous step is outside the target block.ToavoidthewrongchoiceofentranceedgeinthecaseofFig.2, twomeasurescanbeadoptedintheprogram,thefrstistosetcritical distance not too short because the V-V contact theory is more rigid than that of V-E contact;the second is to reduce the vertex displacement during a time step by using a small time interval.

Two concave vertices cannot form a contact,so only two situations are considered in contact detection:contact between two convex vertices,and contact between a convex vertex and a concave vertex.When a convex vertex penetrates a concave one, two edges of the target vertex may be the entrance edge,as shown in Fig.3 where the invading vertexAis within the range of the opposite angle∠CBEof the concave vertex∠FBD.In this case,the shortest distance criterion cannot lead to correct simulation result (Bao and Zhao,2010).The solution of the original DDAtheory tothis case is to add a spring to both edges of the concave.However,this method is not always true,for it would cause the block’sunreasonable rotation called as the“locking phenomenon”(Bao and Zhao,2012).

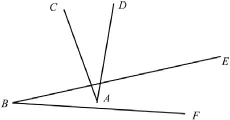
Fig.2.V-V contact or V-E contact?

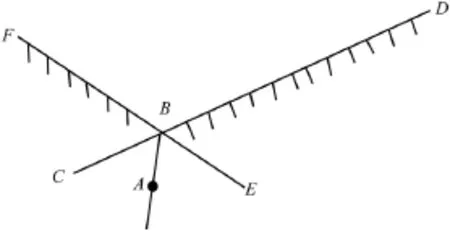
Fig.3.Angle bisector criterion.

To solve this problem,the angle bisector criterion is adopted to determine the entrance edge,i.e.to compare∠FBAand∠ABDshown in Fig.3.If the former is small,FBis the entrance edge;if the latter is small,BDis the entrance edge;and if these two angles are equal,bothBDandFBare entrance edges.

This angle bisector criterion is also applicable to the contact of two convex vertices.In that case,it has the same essence as the shortest distance criterion.Therefore,the shortest distance criterion is actually replaced by the angle bisector criterion in the modifed method.

5.Augmented Lagrangian method

The penalty method was originally used in the DDA method to enforcecontactconstraints atblockinterfaces,andthecontactforce was also calculated with the penetration depth.However,many researchersfound that the accuracy of the contact solution depends highlyonthechoice of thepenaltynumberandtheoptimal number cannot be explicitly found beforehand.Lin et al.(1996)proposed an ALM to overcome the above disadvantage.The essential concept behind the ALM is to use both a penalty numberpand a Lagrange multiplierλ(λrepresents the contact force)to iteratively calculate the contact force until the distancedof penetration of one block into the other is below a minimum tolerance and the residual force between block contacts is also below another minimum tolerance. An updated value ofλcan be written as follows:

Based on the principle of the minimum potential energy,submatrices derived from springs and contact forces should be added to the global equations,and the relevant formulae can be found in Lin et al.(1996).

We simulate again the example of block sliding along incline with ALM,as indicated in Fig.1.The parameters are the same as the example in Section 2,except the friction angleφbeing 35°.When the spring stiffnesspis 107Pa and 109Pa,respectively,displacements of vertexAof the sliding block after 2-5 iterations are listed in Table 3.The analytical solution of displacement is 0.736 m.Therelative errors are also listed in the table.From the results,we fnd that even whenp=E/5000 reliable results can still be achieved.

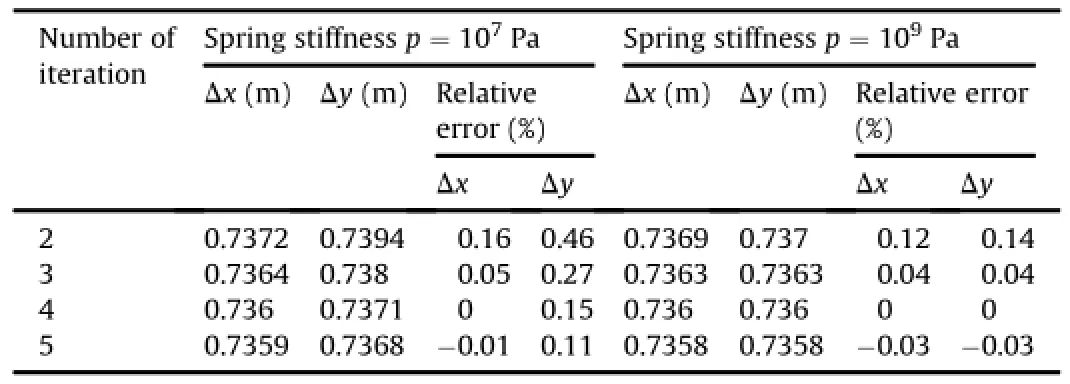
Table 3Displacement of vertexAversus iterations by using ALM.

Fig.4.Forces acting on a sliding block.

From Eq.(2),we know that the essential of ALM is to separate contact force from spring force.The sum of contact force and spring force of iterationkis the contact force of iterationk+1.After several iterations,the spring force and the penetrating depth will become very small.So the penetrating depth after iterations can represent the tolerance of ALM.

Contact forces acting on a rectangle sliding along an incline has been analyzed by Yeung(1991).For the block of right-angledisosceles triangle with edge length of 3 m in Fig.1,the contact forces can be derived in the same way.Distributed forces along edgeABinclude normal contact force and sliding friction force. They are represented by four forces acting at verticesAandB,as shown in Fig.4.NAandfAare the equivalent normal and friction forces acting at vertexA,whileNBandfBare those at vertexB.Fis the inertial force.Gis the gravity.From the equilibrium equations of the sliding block,we can get:

ForM=2.7×103kg/m2andφ=35°,the analytical solutions of normal contact forces are as follows:NA=3.2258× 104N,NB=5.1902×104N.

ALM and penalty method with and without open-close iteration are adopted respectively in this modifed DDA method.The penetrating depths and normal contact forces are listed in Table 4.The analytical solutions ofΔxAandΔyAare both 0.736 m,and those of normal contact forces for verticesAandBare 3.2258×104N and 5.1902×104N,respectively.From Table 4,we know that ALM is better than penalty method in displacement calculation and in contact force calculation except the case ofp=107Pa.For the spring stiffness ofp=109Pa,the penetrating depths obtained by ALM are about 1/4 of those by penalty method.We also fnd that penalty method without iteration provides almost the same results as penalty method with iteration.

6.Validation examples

6.1.Example 1

As shown in Fig.5a,there are two isosceles triangle blocks which touch each other at a point.The bottom block is fxed.Thisexample is simulated by using the original DDA code.At the 240th step,the V-V contact pair is locked,and the upper block rotates anticlockwise(Fig.5b).Until the 300th step,the upper block begins to slide along the lower block(Fig.5c).These behaviors do not conform to ideal or practical situation.Since in ideal situation,the upper block can stay balance,and in practical situation the upper block would not rotate around a fxed vertex.

Table 4Penetrating depths and normal contact forces obtained by ALM and penalty method.

To validate the modifed method,an example using angle bisector criterion is presented in Fig.6.There are two isosceles triangle blocks in the system and the bottom block is fxed.This is a modifed example of Bao and Zhao(2010).The infuence of gravity is concerned.The simulation shows that the upper block can stay motionless at any time.

6.2.Example 2

Fig.7 presents a complex example for the modifed DDA.In this example,10 blocks rest along a double incline.These blocks begin to slide under the action of gravity.The contact relationships among the block system are much complex.Fortunately,the simulation result is reasonable.It means that this example verifes the ability of the modifed DDA method.

Fig.5.Results of simulation by using the original DDA code.

Fig.6.Example of two isosceles triangle blocks.

7.Conclusions

The modifed DDA method and the complete simulation process presented in this paper can omit open-close iterations and does not need to recognize the contact patterns and the transform among them,making the simulation quick and simplifed.For the contact with invading vertexon the angle bisector,two springs are added to both edges of the target vertex,so that the DDA code can correctly treat this special V-V contact.For both ALM and penalty method, the spring stiffness can be smaller than Young’s modulus;and in ALM,the penetrating depths can be signifcantly less than those of penalty method.

Blocks are temporarily separated in this study.For jointed rock mass,if a proper criterion such as Mohr-Coulomb theory is implemented into the friction matrix,the modifed DDA method can simulate the fracture process of rock mass.

Fig.7.Simulation of 10 blocks sliding along a double incline.

Confict of interest

The authors wish to confrm that there are no known conficts of interest associated with this publication and there has been no signifcant fnancial support for this work that could have infuenced its outcome.

Acknowledgments

This work is supported by CRSRI Open Research Program(No. CKWV2014206/KY)and the National Basic Research Program of China(No.2011CB710603).

Bao H,Zhao Z.An alternative scheme for the corner-corner contact in the twodimensional discontinuous deformation analysis.Advances in Engineering Software 2010;41(2):206-12.

Bao H,Zhao Z.The vertex-to-vertex contact analysis in the two-dimensional discontinuousdeformation analysis.Advancesin Engineering Software 2012;45(1):1-10.

Beyabanaki SAR,Jafari A,Biabanaki SOR,Yeung MR.Nodal-based three-dimensional discontinuous deformation analysis(3-D DDA).Computers and Geotechnics 2009;36(3):359-72.

Beyabanaki SAR,Mikola RG,Hatami K.Three-dimensional discontinuous deformation analysis(3-D DDA)using a new contact resolution algorithm.Computers and Geosciences 2008;35(3):346-56.

Cheng YM,Zhang YH.Rigid body rotation and block internal discretization in DDA analysis.International Journal for Numerical and Analytical Methods in Geomechanics 2000;24(6):567-78.

Hsiung SM.Discontinuous deformation analysis(DDA)withnth order polynomial displacement functions.In:Elsworth D,Tinucci JP,Heasley KA,editors.Rock mechanics in the national interest,Proceedings of the 38th US Rock Mechanics Symposium.Rotterdam,Washington,DC:A.A.Balkema;2001.p.1437-44.

Ke TC.Modifcation of DDA with respect to rigid body rotation.In:Li JC,Wang CY, Sheng J,editors.Proceedings of the 1st International Conference on analysis of discontinuous deformation.Chungli,Taiwan,China:National Central University;1995.p.260-73.

Keneti AR,Jafari A,Wu JH.A new algorithm to identify contact patterns between convex blocks for three-dimensional discontinuous deformation analysis. Computers and Geotechnics 2008;35(5):746-59.

Koo CY,Chern JC,Chen S.Development of second order displacement function for DDA.In:Li JC,Wang CY,Sheng J,editors.Proceedings of the 1st International Conference on analysis of discontinuous deformation.Chungli,Taiwan,China: National Central University;1995.p.91-108.

Lin CT,Amadei B,Jung J,Dwyer J.Extensions of discontinuous deformation analysis for jointed rock masses.International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts 1996;33(1):671-94.

Liu J,Geng QD,Kong XJ.A fast common plane identifcation algorithm for 3D contact problems.Computers and Geosciences 2009;36(1-2):41-51.

MacLaughlin MM,Doolin DM.Review of validation of the discontinuous deformation analysis(DDA)method.International Journal for Numerical and Analytical Methods in Geomechanics 2006;30(4):271-305.

MacLaughlin MM,Sitar N.Rigid body rotations in DDA.In:Salami MR,Banks D, editors.Proceedings of the 1st International Forum on DDA and simulations of discontinuous media.Berkeley,California,USA:TSI Press;1996.p.620-36.

Ning YJ,Yang J,Ma GW,Chen PW.Contact algorithm modifcation of DDA and its verifcation.In:Ma GW,Zhou YX,editors.Analysis of discontinuous deformation:new developments and applications.Singapore:Nanyang Technological University;2009.

Shi GH.Discontinuous deformation analysis-a new numerical model for the statics and dynamics of block systems.PhD Thesis.Berkeley:University of California;1988.

Wang XB,Ding XL,Lu B,Wu AQ.DDA with higher order polynomial displacement functions for large elastic deformation problems.In:Proceedings of the 8th International Conference on the analysis of discontinuous deformation,Beijing, China;2007.p.89-94.

Wu JH.Compatible algorithm for integrations on a block domain of any shape for three-dimensional discontinuous deformation analysis.Computers and Geotechnics 2010;37(1-2):153-63.

Yeung MR,Jiang QH,Sun NA.A model of edge-to-edge contact for threedimensional discontinuous deformation analysis.Computers and Geotechnics 2007;34(3):175-86.

Yeung MR.Application of Shi’s discontinuous deformation analysis to the study of rock behavior.PhD Thesis.Berkeley:University of California;1991.

Yong Yu obtained his BSc degree in mining engineering from Xi’an University of Architecture and Technology in 1990 and his PhD in rock mechanics from the University of Science and Technology Beijing in 1996.After a six-year period of working in the Rock Foundation Division at the Yangtze River Scientifc Research Institute in Wuhan,he has been working in School of Mechanics and Engineering of Southwest Jiaotong University since 2002.From November 2008 to November 2009,he worked as a visiting scholar in the Department of Civil and Architecture Engineering at Royal Institute of Technology(KTH),Stockholm,Sweden.He has published about 30 technical journal papers in English or Chinese.His contribution in rock mechanics was a modifed Brazilian test.His research interests cover the whole feld of rock mechanics,but are currently concentrated on discontinuous deformation analysis(DDA).

*Corresponding author.Tel.:+86 13551017371.

E-mail address:yuyong2000@126.com(Y.Yu).

Peer review under responsibility of Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.

1674-7755©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

http://dx.doi.org/10.1016/j.jrmge.2014.12.001