Review of methods for predicting in situ volume change movement of expansive soil over time

Hana H.Adem,Sai K.Vanapalli

Department of Civil Engineering,University of Ottawa,Ottawa,Ontario,Canada

1.Introduction

Expansive soils absorb large quantities of water after rainfall or due to local site changes(such as leakage from water supply pipes or drains),becoming sticky and heavy.Conversely,they can also become stiff when dry,resulting in shrinking and cracking of the ground.This hardening-and-softening is known as ‘shrink-swell’behavior(Jones and Jefferson,2012).When supporting lightly loaded structures,the effect of significant changes in moisture content on soils with a high shrink-swell potential can be severe.Hence,it is important to provide tools for practitioners to reliably estimate the volume change behavior of expansive soils in field.Significant advances were made during the last half-a-century towards prediction of the heave and the shrink related volume change behavior of expansive soils.The focus of most of the prediction methods proposed in the literature however has been towards estimating the maximum heave potential which occurs when the soil attains the saturation condition.Rao et al.(2011),Vanapalli and Lu(2012),and Vanapalli and Adem(2012)summarized a number of methods for the prediction of heave potential of soil.These methods are valuable;however,they do not provide information of soil movements in the field over time.The soil moisture changes due to environmental changes or other factors have a significant influence on the soil movement changes with time.For this reason,information related to the soil movement over time is of practical interest for both the reliable design of foundations for structures on expansive soils and the assessment of pre-wetting and controlled wetting mitigation alternatives for expansive soils.

Research particularly in the past fifteen years has been directed by various investigators to propose methods for the prediction of the soil movement over time(e.g.Alonso et al.,1999;Briaud et al.,2003;Vu and Fredlund,2004,2006;Zhang,2004;Wray et al.,2005;Overton et al.,2006;Nelson et al.,2007;Adem and Vanapalli,2013).Briaud et al.(2003)suggested that any method developed to predict the movement of expansive soils over time must include two components:(i)the range of water content or soil suction fluctuations as a function of time within the active zone depth;and(ii)the constitutive law that links the soil state variables(i.e.water content,soil suction,or mechanical stress)to the volume change movement of the soil.The current methods of the prediction of soil movement over time can be classified into three categories based on the state variables used in their constitutive laws:(i)consolidation theory-based methods that use the matric suction and the net stress as state variables(i.e.extending the two independent stress state variables concept proposed by Fredlund and Morgenstern(1977)),(ii)water content-based methods that use the soil water content as a state variable,and(iii)suction-based methods that use the matric suction as a state variable.

The aim of this paper is to review the state-of-the-art of methods for predicting the in situ volume change movement of expansive soil with respect to time.The current prediction methods are succinctly summarized and critically reviewed.

2.Consolidation theory-based methods

The volume change behavior of an unsaturated soil primarily involves two processes,i.e.the transient water flow process and the soil volume change process.These two processes are linked to each other by the coupled consolidation theory of unsaturated soils.The rigorous formulation for consolidation(i.e.volume change)of unsaturated soils requires the continuity equation coupled with the equilibrium equations(Fredlund and Hasan,1979;Dakshanamurthy and Fredlund,1980;Lloret and Alonso,1980;Dakshanamurthy et al.,1984;Lloret et al.,1987;Fredlund and Rahardjo,1993;Wong et al.,1998;Vu and Fredlund,2002).These equations require constitutive relations for the volume change of unsaturated soils as well as flow laws for fluid phases(air and water phases).The volume change constitutive relations/models for unsaturated soils fall into two categories,i.e.elastic models and elastoplastic models.The elastic models relate strain increments to increments of net stress and matric suction.Such models have been proposed by Fredlund and Morgenstern(1976)and Lloret et al.(1987).The elastoplastic constitutive models have been also developed for unsaturated soils.One of the first elastoplastic constitutive models developed for unsaturated soils was the Barcelona Basic Model(BBM)(Alonso et al.,1990),which was based on the theoretical framework proposed by Alonso et al.(1987).The concept allows the reproduction of many important features of unsaturated soil behavior,such as collapse upon wetting,and is the basis upon which most other elastoplastic models have been developed.Those volume change constitutive models adopt the idea of two independent stress variables,i.e.the net stressσ-uaand the soil matric suction ua-uw,whereσis the total normal stress,uais the pore air pressure,and uwis the pore water pressure.

2.1.Methods based on elastic constitutive models

Several researchers(Biot,1941;Coleman,1962;Matyas and Radhakrishna,1968; Barden et al.,1969; Aitchison and Woodburn,1969;Brackley,1971;Aitchison and Martin,1973;Fredlund and Morgenstern,1976,1977;Lloret et al.,1987)developed volume change constitutive relationships based on the assumption that the soil is elastic in nature for a large range of loading conditions.Two constitutive relationships have been suggested for describing the deformation state of unsaturated soils.One constitutive relationship has been formulated for soil structure(in terms of void ratio or volumetric strain)and the other constitutive relationship has been formulated for water phase(in terms of degree of saturation or water content).

By assuming that the soil behaves as an incrementally isotropic,linear elastic material(i.e.an incremental procedure using small increments of stress-strain can be used to apply the linear elastic formulation to a non-linear stress versus strain relationship(Fredlund and Rahardjo,1993)),the soil structure constitutive relation associated with the volumetric strain can be written as

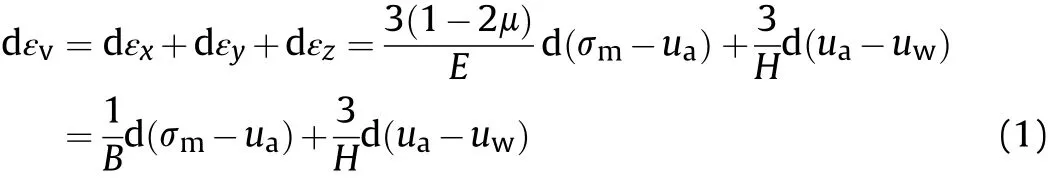
where εvis the volumetric soil strain; εx,εy,and εzare the normal strains in the x-,y-,and z-directions,respectively;σmis the mean total normal stress,and σm=(σx+ σy+ σz)/3,in which σx,σy,and σzare the normal stresses in the x-,y-,and z-directions,respectively;μ is the Poisson’s ratio;E is the modulus of elasticity for the soil structure with respect to a change in net normal stress;H is the modulus of elasticity for the soil structure with respect to a change in matric suction;and B is the bulk modulus of soil.

The constitutive equation for the water phase defines the water volume change in the soil element for any change in the total stress and matric suction.By assuming that water is incompressible,the constitutive equation for the water phase can be formulated as a linear combination of the stress state variables changes as follows(Fredlund and Morgenstern,1976):

where Vwis the volume of water in the soil element;V0is the initial overall volume of soil element;σx-ua,σy-ua,and σz-uaare the net normal stresses in the x-,y-,and z-directions,respectively;Ewis the water volumetric modulus associated with a change in net normal

stress;and Hwis the water volumetric modulus associated with a change in matric suction.

Fredlund and Morgenstern(1976)also provided the following constitutive relationships for volume change of soil structure and water phase in a compressibility form:where ms1and ms2are the coefficients of total volume change with respect to a change in net normal stress and a change in matric suction,respectively;mw1and mw2are the coefficients of pore water volume change with respect to a change in net normal stress and a change in matric suction,respectively.The coefficients of total volume changes can be calculated from constitutive surfaces for void ratio and water content of soil.

Comparing Eqs.(1)and(2)with Eqs.(3)and(4),the relationships among the volume change coefficients are written as follows:

In a three-dimensional(3D)consolidation problem,there are five unknowns of deformation and volumetric variables to be solved.These unknowns are the soil displacements in the x-,y-,and z-directions,the water volume change,and the air volume change.The soil displacements are used to compute the total volume change of soil.The five unknowns can be obtained from three equilibrium equations for the soil structure and two continuity equations(water and air phase continuities).However,the pore air pressure is generally assumed to be atmospheric and remains unchanged during the consolidation process.In this case,only the stress equilibrium condition and the water flow continuity need to be considered in the analysis.

(1)Equilibrium equations for soil structure

The stress state for an unsaturated soil element should satisfy the following equilibrium condition:whereσij,jis the component of the net total stress tensor,bjis the component of body force vector.

The strain-displacement equation for soil structure of an unsaturated soil is given as follows:

where εijis the component of the strain tensor,uiis the component of soil displacement in thei-direction.

By substituting the strain-displacement equation(Eq.(7))and the stress-strain relationship(Eq.(1))into the equilibrium equation(Eq.(6)),the differential equations for soil structure for general 3D problems can be written as

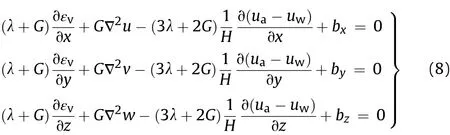
whereGis the shear modulus,andG=E/[2(1+μ)];u,v,andware the displacements in thex-,y-,andz-directions,respectively;bx,by,andbzare the body forces in thex-,y-,andz-directions,respectively;λ= μE/[(1+ μ)(1-2μ)];∇2= ∂2/∂x2+ ∂2/∂y2+ ∂2/∂z2.

(2)Water continuity equation

The water continuity equation for unsaturated soils,assuming that water is incompressible and deformations are incrementally in finitesimal,can be written as(Freeze and Cherry,1979)

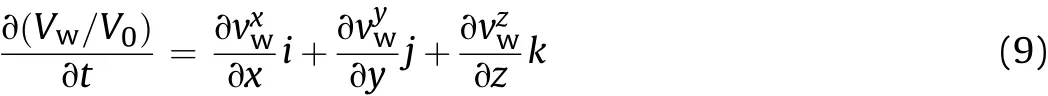
where ∂(Vw/V0)/∂tis the net flux of water per unit volume of the soil,tis the time,andvw=vxwi+vywj+vzwkis the Darcy’s flux which relates to the hydraulic head(i.e.pressure head plus elevation head)using Darcy’s law:

wherevwiis the Darcy’s flux in thei-direction,kwiis the hydraulic conductivity in thei-directionwhich is a function of matric suction,ρwis the density of water,gis the gravitational acceleration,andYis the elevation.

The differential equation for water phase(Eq.(11))was derived by substituting the time derivative of the water phase constitutive equation(Eq.(2)or(4))and Darcy’s law(Eq.(10))into the water phase continuity equation(Eq.(9))(Fredlund and Hasan,1979):

wherekxw,kyw,andkzware the hydraulic conductivity functions in thex-,y-,andz-directions,respectively.

Eq.(11)was further derived by extending Biot’s consolidation theory for saturated soils(Biot,1941).Eq.(1)(or Eq.(3))was solved for d(σm-ua)in terms of dεvand d(ua-uw).The term d(σm-ua)was then substituted into Eq.(2)(or Eq.(4))(Fredlund and Rahardjo,1993).The volumetric water content variation can be expressed as

Eqs.(8)and(13)together are the differential equations for the coupled consolidation for unsaturated soils that can be used to predict the volume change behavior of unsaturated expansive soils(Fredlund and Rahardjo,1993).

2.1.1.Vu and Fredlund(2004)method

Vu and Fredlund(2004)extended the general consolidation theory of unsaturated soils and proposed a method for the prediction of one-dimensional(1D),two-dimensional(2D),and 3D soil heave over time.The governing equations for soil structure(Eq.(8))and for water phase(Eq.(13))were solved numerically using uncoupled and coupled analyses.In the uncoupled analysis,Eq.(8)was solved independently from Eq.(13).A general-purpose partial differential equation solver(FlexPDE)was used to obtain the uncoupled solution.First,the distribution of soil matric suction over time for specified boundary conditions was determined.Then,the soil heave due to the applied boundary conditions and the change in matric suction was calculated.However,in the coupled analysis,the governing equations were solved simultaneously using a finite element computer program(COUPSO)(Pereira,1996).The analysis results include soil heave and matric suction changes obtained during the transient process.The uncoupled solutions can be achieved with a relative ease than the coupled solutions,because the non-linear functions of soil properties involved in water flow or stress deformation process are considered to be independent of one another.

A case history of a fl oor slab of a light industrial building located in Regina,Saskatchewan,Canada,was used by Vu and Fredlund(2004)to test the validity of their prediction method.Fig.1 provides the comparison between the soil heave predicted by Vu and Fredlund(2004)at various matric suction conditions over time and the total heave measured by Yoshida et al.(1983)at the surface of the slab.The total heave predicted under the steady state condition agrees well with the measured heave.

Vu and Fredlund(2006)investigated the challenges encountered by Vu and Fredlund(2004)to characterize the void ratio at low net normal stresses and/or low matric suctions.Extremely low elastic moduli are possible for low net normal stresses or low matric suctions which contribute to unreasonably large soil movements.These challenges were overcome by providing a continuous,smooth void ratio constitutive surface based on the soil swelling indices obtained from the conventional oedometer tests.Two typical volume change problems,water leakage from a pipe under a fl exible cover and water in filtration at the ground surface,were solved by Vu and Fredlund(2006)using both the coupled and uncoupled analyses.It was suggested that an uncoupled analysis may be adequate for most heave predictionproblems.However,the coupled analysis provides a more rigorous understanding of the swelling behavior of expansive soils.

The prediction method presented in Vu and Fredlund(2004,2006)was validated using Regina expansive clay.The predicted results were in a reasonable agreement with the measured values.The method focused on the prediction of soil heave corresponding to a short-term condition.The soil shrinkage corresponding to a long-term condition was neglected.Determination of the coefficients of volume change ms1,ms2,mw1,and mw2requires the void ratio and water content constitutive surface to be constructed.Those constitutive surfaces were obtained from the consolidation tests or triaxial tests with suction control.However,such tests are time consuming and require advanced laboratory equipment which is expensive.

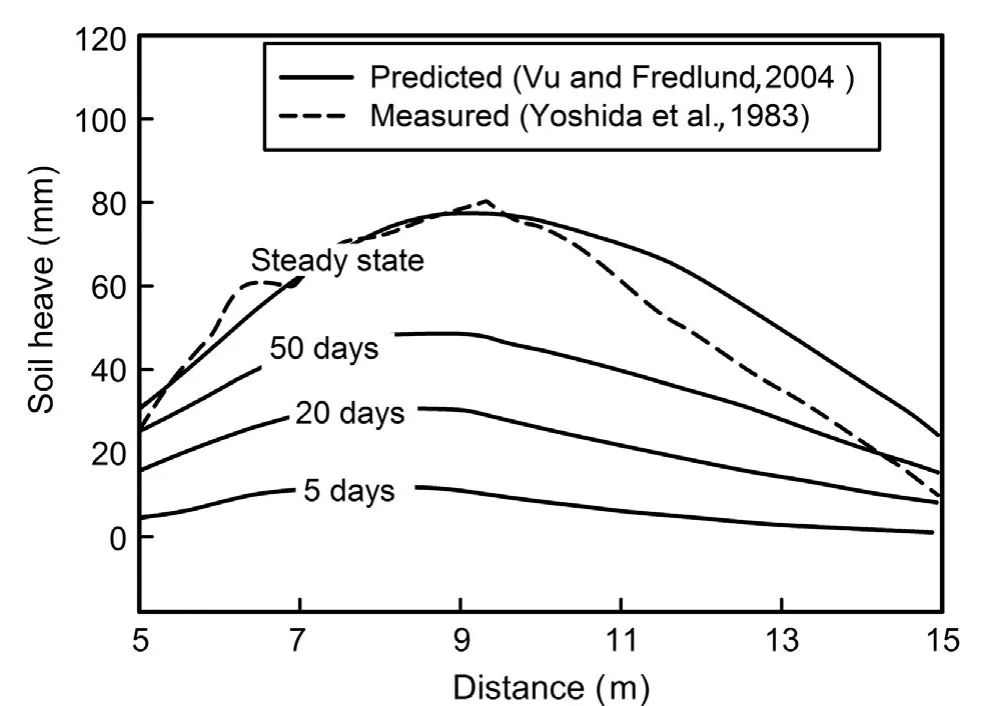
Fig.1.Measured and predicted heaves at the surface of the slab(modified after Vu and Fredlund(2004)).

2.1.2.Zhang(2004)method

Unsaturated soils attain saturated condition under different scenarios;however,researchers were unable to provide a unified theoretical framework for both saturated and unsaturated soils.Several investigators provided the coupled consolidation theory for saturated and unsaturated soils,separately.The concept of the constitutive surfaces,however,has been provided only for unsaturated soils because of the following reasons(Zhang et al.,2005):(i)volume change theory for saturated soils is well established through the research work of Terzaghi(1936)and Biot(1941).Both Terzaghi(1936)and Biot(1941)have suggested using the consolidation curve and have not used the constitutive surfaces for saturated soils;(ii)many researchers use a single stress state variable(i.e.the effective stress)for interpreting the behavior of saturated soils.

Zhang(2004)provided the coupled consolidation for both saturated and unsaturated soils in a unified manner using the constitutive surfaces.Thermodynamic analogue was used to explain the coupled consolidation process for saturated and unsaturated soils following Terzaghi’s1D consolidation theory(Terzaghi,1943)for saturated soils.The differential equation of Terzaghi’s consolidation theory is identical to the differential equation for non-stationary 1D flow of heat through isotropic bodies.The loss of water(consolidation)corresponds to the loss of heat(cooling)and the absorption of water(swelling)to an increase of heat content of a solid body(Zhang,2004).In other words,the pore water pressure corresponds to the temperature while the water content to the heat energy per unit mass.The coupled consolidation theory for saturated and unsaturated soils includes the differential equations for soil structure and water phase.The differential equation for soil structure is given in Eq.(8).However,to derive the differential equation for water phase,it was assumed that the continuity equation for the water phase is similar to that for heat transfer(i.e.using thermodynamics principles).As a consequence,the differential equation for water phase can be written in terms of specific water capacity of a soil(i.e.the volume of water required decreasing unit mass of soil by 1 kPa of matric suction):whereρdis the dry unit mass of a soil and Cwis the specific water capacity of a soil.

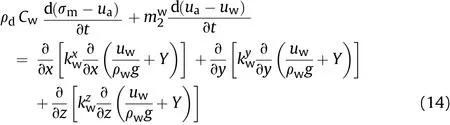
Eqs.(8)and(14)are the differential equations for the coupled hydro-mechanical stress(consolidation)problem for unsaturated soils.However,by using the constitutive surfaces proposed by Zhang(2004)for saturated and unsaturated soils,Eqs.(8)and(14)can also be used for saturated soils as a special case.Two stress state variables(i.e.total stress and pore water pressure)were used for saturated soils in order to develop the constitutive surfaces for both saturated and unsaturated soil mechanics in a unified system with smooth transition.

Close examination shows Eqs.(13)and(14)are the same;the left sides of both equations are the volumetric water content variation and the right sides represent the net water flow into the soil element.Eq.(14)can be used to simulate the water generation by the heat generation based on the thermodynamic analogue.Consequently,some already well-established commercial software packages(e.g.Abaqus,SUPER,and ANSYS)for solving those coupled thermal stress problems can be modified for solving the complicated coupled consolidation problems related to geotechnical engineering(Zhang,2004).

For the simulation of volume change behavior of the soils,the coupled hydro-mechanical stress analysis was used and the thermodynamic part was corresponding to the water phase continuity of the soil.By applying initial and boundary conditions and using one of the finite element methods to solve the differential equations of the coupled consolidation theory(Eqs.(8)and(14)),the net stress and the matric suction can be calculated.The calculated net stress and the matric suction were used as an initial condition for the next step.This simulation technique can be continuously performed to predict the soil movement over time.

Zhang(2004)modeled a site in Arlington,Texas,USA,extending the coupled consolidation theory of saturated-unsaturated soils for estimation of the soil movement over time.Four full-scale spread footings,referred to as RF1,RF2,W1,and W2,constructed on expansive soils of the Arlington site were modeled over a period of 2 years.Factors that influence the movements of expansive soils such as the daily weather data and the vegetation were considered for this field construction site.Abaqus/standard program was used for the simulation of the soil movement at the Arlington site based on several models,including the coupled consolidation theory for saturated-unsaturated soils,potential and actual evapotranspiration estimation by using daily weather data,theories for the simulation of the soil-structure interaction at the soil-slab interface.The soildomain considered in the simulation was 10 m×10 m×4 m(length×width×height).Three different material properties were considered in the modeling,which include a concrete footing(2 m×2 m×0.6 m),dark gray silty clay(with a depth of 0-1.8 m),and brown silty clay(with a depth of 1.8-4 m).The same site was also modeled by Briaud et al.(2003)to investigate the damage caused by expansive soils to both concrete and asphalt pavements.More details of the Arlington site are available in Briaud et al.(2003)and Zhang(2004).

Fig.2 shows the average values of the predicted soil movements at the four corners of the modeled footing,the measured movements of the four footings,and the average values of the measured movements of the footings over the two-year period.The comparison of the predicted movements with the measured movements of each footing did not lead to as good a comparison as that based on the average values of the measured movements of the four footings.This could be attributed to the fact that regular measurements of soil movement can vary significantly while the average measurements are more representative of the actual variation in the movement of the soil site(Zhang,2004).

Zhang(2004)methodisacomprehensiveapproachfor modeling the water flow and the soil movement over time.Complex numerical solutions in finite element computer programs are required in this approach to address the analogy between the thermal and hydraulic problems.The use of constitutive surfaces in this approach contributed to using a unified system for the first time to simulate the volume change behavior of expansive soils under both saturated and unsaturated conditions.However,there are limitations to apply the 3D constitutive surface model in practice.The proposed constitutive surfaces have been developed based on testing soils under conditions not typically experienced in the field such as shrinkage or matric suction test at no normal stress,or a consolidation test at saturated conditions.Also,conventional laboratories are not equipped to conduct shrinkage tests or matric suction tests which are required for constructing the constitutive surface of unsaturated soils.These tests are time consuming that require sophisticated laboratory equipment and trained personnel.

2.2.Methods based on elastoplastic constitutive models

The elastic models developed for predicting the volume change of unsaturated soils are relatively easy to implement within numerical analysis;however,there are some limitations.The most important limitation is that there is no distinction between reversible and irreversible strains,which means that they can only be used in problems that involve only monotonic loading and unloading(Wheeler and Karube,1996).Consequently,a variety of elastoplastic constitutive models have been introduced and studied(e.g.Alonso et al.,1987,1990;Karube,1988;Gens and Alonso,1992;Kohgo et al.,1993;Modaressi and Abou-Bekr,1994;Cui et al.,1995;Delage and Graham,1995;Kato et al.,1995;Wheeler and Sivakumar,1995;Bolzon et al.,1996;Blatz and Graham,2003;Chiu and Ng,2003;Wheeler et al.,2003;Tamagnini,2004;Thu et al.,2007;Sheng et al.,2008).Lloret and Alonso(1980)established that the constitutive models based on the concept of elastoplasticity provide a better understanding and explanation of expansive soil behavior;in particular,those features concerning stress path dependency and soil collapse upon wetting.Alonso et al.(1990)proposed an elastoplastic constitutive model for unsaturated soils(i.e.BBM).The BBM can be regarded as potentially one of the most comprehensive formulations since it incorporates both swelling and collapse behaviors of unsaturated soil in a unified comprehensive manner(Thomas and He,1998).The model was formulated within the framework of hardening plasticity using two independent stress variables:the net stress and the soil matric suction.The model was fully described in Alonso et al.(1990).Only succinct details will therefore be summarized here.

The BBM is characterized by two yield curves whose hardening laws are controlled by total plastic volumetric deformation(Fig.3).For isotropic stress conditions,the two yield surfacesF1,F2are de fined in terms of the following stress variables:net mean stressp=(σ1+ σ2+ σ3)/3-ua,deviator stressq= σ1- σ3,and matric suctions=ua-uw.The first,known as the loading collapse(LC)yield surface,is related to irreversible compression that can occur on an increase of load(loading strains)or decrease of suction(collapse strains):

Fig.2.Soil movement predicted by Zhang(2004)method and the soil movements measured at the Arlington site over two years(modified after Zhang(2004)).

whereMis the slope of the critical state line as indicated in Fig.3,psis the parameter related to the effect of suction on the cohesion of the soil,andp0is the preconsolidation stress at the current value of suction.In Eq.(15),the parameterspsandp0depend on the suction,which are de fined as follows:

Fig.3.Yield surface of Barcelona basic model(BBM)(modified after Alonso et al.(1990)).

wherekis the parameter describing the increase in cohesion with suction;p*0is the preconsolidation stress at zero suction(saturated condition);pcis the reference stress;κis the normal swelling index;and λ(s)and λ(0)are the compression indices of the soil at the current value ofsand at the saturated condition(s=0),respectively.λ(s)varies with suction according to:

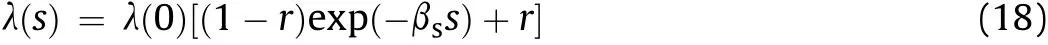
whereβsandrare the soil parameters.Withp0andpsvarying with suction,Eq.(15)describes a family of elliptical yield curves associated with different suction values.

The second yield equation,known as the suction increase(SI)yield surface(Fig.3),is related to the irreversible compression that can occur on increase of suction(drying):

wheres0is the maximum previously attained value of the suction.

Changes of stress and suction within the yield surfaces are accompanied by recoverable deformations.For convenience,it is assumed that the soil is elastic and isotropic within the yield surfaces.The elastic component of volumetric strain is given by

whereκsis the suction swelling index,eis the void ratio,andpatmis the atmospheric pressure(i.e.101.3 kPa).

Once the net mean stresspreaches the yield valuep0,the plastic component of volumetric strain caused by yielding on the LC yield surface is given by

Similarly,with an increase in suction,if the yield locuss=s0is reached,the following plastic volumetric strain caused by yielding on the SI yield surface will be induced:

Irreversible deformations control the position of the LC and SI yield surface through Eqs.(21)and(22).This type of hardening implies an independent motion of both yield curves in the(p,s)stress space.However,some experimental evidence suggests a de finite coupling between them(Alonso et al.,1990).A simple way to couple both yield curves results if their position is controlled by the total plastic volumetric deformation,dεpv=dεpvs+dεpvp.Then,from Eqs.(21)and(22)the hardening laws are proposed as follows:

The BBM is considered to be a suitable model for unsaturated soils and is thus implemented by Abed(2008)into the PLAXIS finite element code(Vermeer and Brinkgreve,1995)to predict the movements of expansive soils underneath a trial wall built in Barakat site in Sudan.The wall was made of brick with a length of 1.2 m and a height of 1.9 m above the ground level.The foundation depth was 0.6 m.The field study was originally carried out by Saeed(2004)in order to investigate the effect of soil replacement on the wall vertical movement.The soil was exposed to two successive wetting-drying cycles for a period of about 18 months.Abed(2008)implemented the numerical analysis for a wall(the wall with no replacement)to simulate the behavior of expansive soil itself.The BBM was used as a constitutive model in the analysis.The numerical analyses involve transient unsaturated flow as well as deformation analyses.As the approach was based on uncoupled analysis,the unsaturated ground water flow was first estimated and the resulted suction fields were used for deformation estimations.The PLAXFLOW finite element code(Brinkgreve et al.,2003)was used to simulate the unsaturated ground water flow and to determine the suction variation with time.The transient flow calculations for the in filtration and evaporation processes are very helpful.By applying transient boundary conditions,the variation of a suction pro file with time can be simulated.According to Saeed(2004),the soil was always soaked with water during wetting phase,suggesting an in filtration rate equal to the saturated soil permeability(ksat=0.02 m/d).A high evaporation rate of 10 mm/d was applied during the drying phase to account for the observed severe shrinkage.The initial condition of suction was generated using the PAXFLOW code.The solution was uncoupled in the sense that ground water calculations were performed first.During the simulation,the PLAXFLOW code saved the suction values for each time step.After the flow calculation being done,the PLAXIS code used the suction values for the deformation analysis.The equilibrium was solved and the internal variables were updated for each time step.Fig.4 shows that the calculated deformations are in a good agreement with the measured data for the period of time under consideration,covering a series of drying and wetting cycles.The results clearly show the possibility of simulating the movement of unsaturated expansive soil using finite element method with a suitable constitutive model.However,it should be always emphasized on the comprehensive understanding of the constitutive model being used and its limitations(Abed,2007).

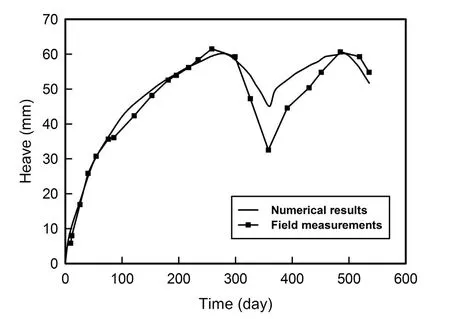
Fig.4.Comparison of the calculated soil movement beneath a trail wall versus the measured data(modified after Abed,2007).

Alonso et al.(1990)and Gens and Alonso(1992)stated that the BBM provides a simple representation of swelling,but is unable to reproduce the large swelling strain exhibited by expansive soils.The model allows only for small reversible swelling in elastic zone.It is therefore intended for use with partially saturated soils of moderate to low plasticity,such as sandy clays,clayey sands and silts,and granular soils.Other models were quickly developed that,while keeping the same core of basic assumptions,sought to improve some of shortcomings of the original BBM.Gens and Alonso(1992)extended the BBM for unsaturated highly expansive clays.The extended framework takes explicitly into account the interaction between a capillary-controlled macrostructure and a microstructure where physicochemical and other phenomena occurring at particle level take place.The distinction between the macrostructure and microstructure provided the opportunity to take into account the dominant phenomena that affect the behavior of each structure in a consistent way.The framework for expansive soils proposed by Gens and Alonso(1992)was based on the combination of the existing classical elastoplastic model(i.e.BBM)with the behavior of active clayey minerals in simple configurations with the purpose of describing the basic features of real expansive soil behavior.Alonso et al.(1999)performed a series of modifications and developments on the framework proposed by Alonso et al.(1990)and Gens and Alonso(1992)to propose an enhanced model,called Barcelona Expansive Model(BExM).Based on the definition of two coupling functions that express the ratio between the microstructural strain and the macrostructural plastic strain,the model allows a good representation of the phenomena of stress-suction path dependency and swelling-shrinkage fatigue during cycles.Comparison with experimental tests performed in a suction-controlled oedometer apparatus shows the ability of the model to capture well the qualitative trends of the data and to adjust them quantitatively in a satisfactory way(Alonso et al.,1999).The validity of the framework,however,needs to be tested by comparing its quantitative predictions with reported results of field tests on expansive soils.

3.Water content-based methods

The soil movement due to environmental changes over time is related to soil suction changes.However,water content is more reliably and easily measured than matric suction and may be sufficient for predicting soil movement(Marr et al.,2004).This section reviews the current water content-based methods for predicting the soil movement as a function of the change in water contentover time.

3.1.Briaud et al.(2003)method

Briaud et al.(2003)proposed a method for estimating the vertical movement(shrink/swell)of the ground surface due to variations in soil water content over time.The soil water content is used as a governing parameter;the range and the depth of water content variations can be estimated from a combination of experiences,databases,observations,and calculations.The shrink test is suggested to obtain the relationship between the change in water content and the volumetric strain induced.Fig.5 shows the typical relationship of water content versus volumetric strain obtained from the shrink test.This relationship can be approximated by a straight line with the slope being the shrink-swell modulus Ew.The ground surface movement for a given timeΔH can be calculated in terms of the shrink-swell modulus and the shrinkage ratio f(i.e.the ratio of the vertical strain to the volumetric strain)using the following equation:

Fig.5.Soil water content versus volumetric strain obtained from the shrink test(modified after Briaud et al.,2003).

where n is the number of soil layers,Hiis the thickness of the ith soil layer,andΔwiis the change in water content as a function of time for the ith layer.More details of this method are available in Briaud et al.(2003).

This shrink test-water content method was evaluated by comparing the predictions with the measurements of the soil movement at the four full-scale spread footings(i.e.RF1,RF2,W1,and W2)constructed in the Arlington site(the same site modeled by Zhang,2004).Specimens were taken at the site during the two year period and data including water content and shrink-swell modulus were measured.Fig.6 shows the comparison between the soil movements predicted by Briaud et al.(2003)method and the measured movements of footings over two years.A better simulation of the field soil movements was achieved using Zhang(2004)method in comparison to Briaud et al.(2003)method.

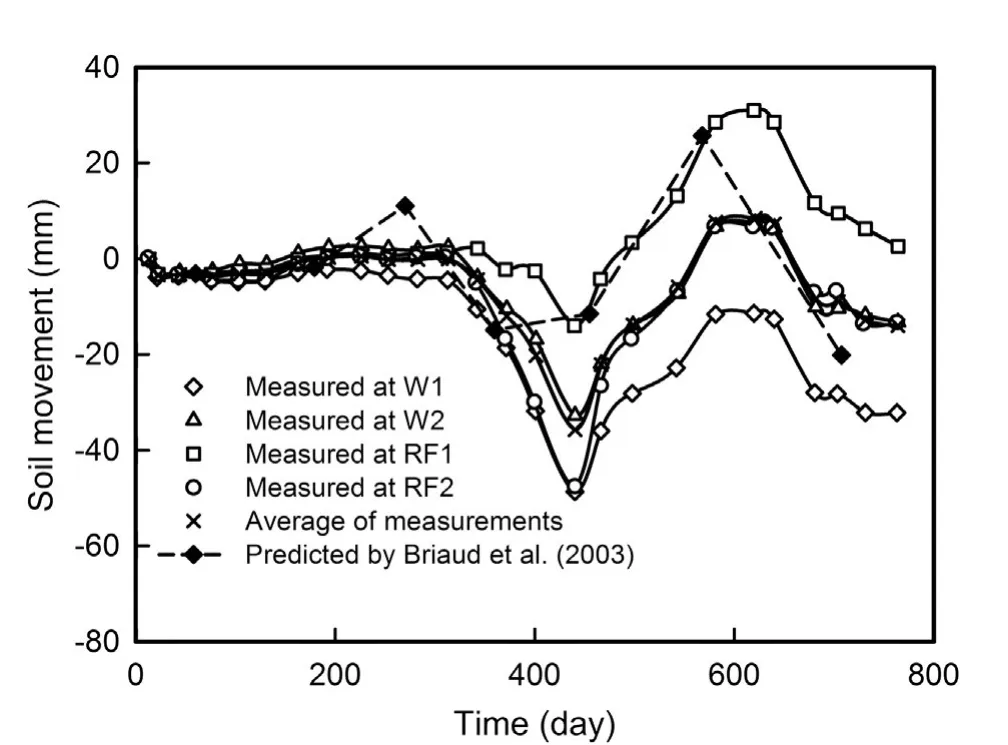
Fig.6.Soil movements predicted by Briaud et al.(2003)method and the measured soil movements at the Arlington site over two years(modified after Briaud et al.,2003).

The advantage of Briaud et al.(2003)method,however,is its capability to predict both the soil swelling and soil shrinkage simultaneously.This method is based on the information of water content which is both reliable and simple to measure in comparison to the soil suction.The constitutive law is obtained from shrink tests on site-specific specimens instead of correlations to the index properties.However,the method is an uncoupled analysis where only the influence of moisture variation is considered.In addition,when the soil is highly fractured,the shrink test is difficult to perform.Another drawback is that any theoretical consideration must make use of the soil-water characteristic curve(SWCC)to transform the governing equations from suction-based equations to water content-based equations(Briaud et al.,2003).

3.2.Overton et al.(2006)method

Overton et al.(2006)presented an approach for predicting the free field heave of expansive soils over time based upon the migration of the wetting front through a soil profile.Analyses of the migration of the wetting front were conducted using the commercial software VADOSE/W(Geo-Slope,2005).VADOSE/W is a finite element program that can be used to model both saturated and unsaturated flows in response to the changes in atmospheric conditions while considering in filtration,precipitation,surface water runoff and ponding,plant transpiration and actual evaporation,and heat flow.The free field heave,which will occur at the ground surface if no stress is applied,is a fundamental parameter in this approach.The free- field heave was predicted using the oedometer method outlined in Nelson and Miller(1992).The general equation for calculating the free field heave is whereρis the free- field heave,CHis the heave index,ziis the thickness of the ith soil layer,σ′fis the in situ effective stress state at the midpoint of the soil layer for the conditions under which heave is being computed,andσ′cvis the swelling pressure from the constant-volumetric oedometer test.

The heave index CHrepresents a relationship between the percent swell that will occur in a soil specimen and the vertical stress applied at the time of inundation.CHcan be determined from the consolidation-swell test and the constant-volume test.Typical results for both types of oedometer tests are shown in Fig.7.In the constant-volume test,the percent swell corresponding to the particular value of inundation stress σ′ishown is%S.At an inundation pressure ofσ′cv,the percent swell is zero.Thus,points B and D fall on the line representing the desired relationship betweenσ′iand%S.This relationship is a straight line(i.e.BD)on a semilogarithmic plot and the slope of that line is CH.

Fig.7.Determination of heave index(modified after Nelson et al.,2007).

The points B and D can be respectively obtained from the consolidation-swell test and the constant volume test.However,this is not practical because it is almost impossible to obtain two identical soil specimens from the field(Nelson et al.,2012).For reliable determination of,Nelson et al.(2006)suggested that several consolidation-swell tests at different inundation pressures along with one constant volume oedometer test would be required.Such an approach is rigorous,but difficult to extend in routine engineering practice.Therefore,to facilitate the use of Eq.(26)and to determine both%S andfrom a single oedometer test,a relationship was developed by Nelson et al.(2006)between the swell pressure from consolidation-swell test,,and the swell pressure from constant volume oedometer test,

The rationale behind Eq.(28)is that the value ofmust fall betweenandby proportionality defined by the value ofλ(Nelson et al.,2012).Nelson et al.(2006)suggested that a reasonable value ofλfor the clay soil in the Front Range area of Colorado,USA,is 0.6.However,the actual value ofλto be used for a soil should be determined specifically.Recently,Nelson and Chao(2014)also developed another relationship(Eq.(29))to relatetobased on observed behavior of expansive soil in oedometer tests:where m is the parameter depending on the particular soil,its expansive nature,and other properties of the soil.

By assuming various values of swelling pressure and percent swell,the maximum free field heave and the depth of potential heave can be calculated.The amount of the heave at any point in a soil profile is a function of the amount by which the water content has increased.The relationship between heave and volumetric water content for a soil can be determined from oedometer tests conducted in a laboratory.For soils that are not fully wetted,the percent swell and the swelling pressure will be less than those measured after the saturation in oedometer tests.Therefore,in calculating soil heave,those values must be corrected for the actual volumetric water content.

The free field heave with respect to time is computed by multiplying the total heave potential(i.e.maximum free heave from Eq.(26))at each soil layer by a heave factor obtained from the heave potential and volumetric water content relationship.The values of the volumetric water content are obtained from VADOSE/W at each time step.The relationship between heave potential and volumetric water content for a soil is determined from oedometer tests.Overton et al.(2006)extended this approach on soil profiles in the Denver area of Colorado with good and poor drainage.Chao et al.(2006)also used this approach to investigate the effect of irrigation practices,poor drainage conditions,deep wetting from underground sources,and dipping bedrock on the heave variations over time.The results showed significant variation in the predicted values of heave potential versus time due to the effect of those factors.

Realistic estimates of the time rate of the migration of the wetting front and the resulting time rate of soil heave can be obtained by Overton et al.(2006)method for only ideal conditions.Such ideal scenarios are only possible where sites have homogenous soil profiles with minimal macroscale fracturing or cracking,and/or where the principal direction of heave is perpendicular to the ground surface.However,if site-specific analyses have not been performed to accurately determine the rate of migration of the wetting front and the resulting time rate of heave,the entire depth of heave potential should be assumed wet during the life of a structure(i.e.maximum heave potential should be considered)(Overton et al.,2006).In addition,the experimental determination of the free- field heave using oedometer tests is both time consuming and difficult to conduct.Some downsides to oedometer tests are related to the extremely long time period required for achieving the equilibrium condition and the difficulty to simulate the in situ conditions(e.g.drainage conditions and lateral pressures).Another drawback of the Overton et al.(2006)method is that it does not give any indication of possible shrinkage.

4.Suction-based methods

Most researchers in the geotechnical engineering field since 1960s described the moisture movement in unsaturated soils in terms of soil suction(e.g.Richards,1965;Lytton and Kher,1970;Mitchell,1979;Pufahl and Lytton,1992;Fredlund,1997;Wray,1998;Fredlund and Vu,2001).Richards(1974)suggested that the soil suction can be used to represent the state of the soil water much more effectively than the water content for two reasons.Firstly,soil suction is primarily controlled by the soil environment and not by the soil itself,and it typically does not exhibit discontinuous trends.The soil suction profile tends towards an equilibrium value at a particular depth under a particular climatic condition while water content is highly sensitive to the soil material variables(e.g.soil type,clay content,soil density,and soil structure).Secondly,the correlation of soil parameters(i.e.permeability or hydraulic conductivity,diffusivity,and shear strength)with water content is poor unless other soil properties such as density and clay content are considered,but these parameters can be conveniently correlated with soil suction.

In suction-based methods,the movement associated with volume change of expansive soils can be evaluated by measuring the present in situ suction condition and estimating(or predicting)possible future suction condition under a certain environment.The basic concept of those methods is that the volume change of unsaturated soils(usually void ratio or vertical strain)is proportional to the suction variation within the range of field conditions.

4.1.Wray et al.(2005)method

Wray et al.(2005)developed a computer program SUCH(it is named from SUCtion Heave)to predict the soil moisture changes and the resulting soil surface movements(heave/shrink),particularly under covered surfaces.The SUCH program includes two models:(i)a moisture flow model for estimating the movement of water through unsaturated expansive soils based on the diffusion equation developed by Mitchell(1979),and(ii)a volume change model developed by Wray(1997)for estimating the vertical soil movement(heave/shrink)associated with the change in soil suction over time.

The Mitchell’s transient suction diffusion equation in 3D takes the form of

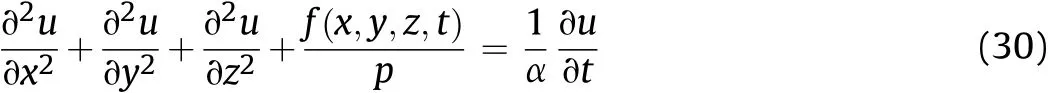
where u is the total soil suction expressed in pF units(1 kPa=0.1×10pF),αis the diffusion coefficient(mm2/s)which can be measured in the laboratory(Mitchell,1979)or calculated from empirical equations(McKeen and Johnson,1990;Bratton,1991;Lytton,1994),p is the unsaturated permeability(mm/s),and f(x,y,z,t)is the internal source of moisture.SUCH program is written in FORTRAN language,utilizing the finite difference technique to solve the transient suction diffusion equation(Eq.(30)).Two main sets of information must be given:(i)the initial condition,i.e.the initial value of suction at each node in the soil mass;and(ii)the boundary conditions,i.e.the values of suction on the boundaries of the soil mass at each time step.Then,the moisture flow model can be used to determine the distribution of soil suction in the soil mass over time.

After the determination of suction distribution through the unsaturated expansive soil mass,the resulting vertical soil movement at each nodal point associated with the change of soil suction over time can be estimated.Suction-based model(Eq.(31))developed by Wray(1997)was used for the estimation of the resulting soil movements:whereΔHi,j,kis the incremental volume change(heave/shrink)at grid point(i,j,k)over the increment thickness Δz; Δz is the incrementthickness in the z-direction over which heave or shrink occurs;γhi,j,kis the suction compression index at grid point(i,j,k),McKeen(1980),Lytton(1994),and Wray(1997)presented different methods to estimate the value ofγhi,j,k;ΔpFi,j,kis the change of total soil suction expressed in pF units at grid point(i,j,k),andΔpPi,j,kis the change of soil overburden over the increment thicknessΔz at grid point(i,j,k).The vertical movement of each nodal point at the top surface of the soil mass was calculated by summation of the vertical movements of the nodal points on the vertical line passing through that surface point extending from the top to the bottom of the active zone of the soil mass(Wray et al.,2005).

Wray et al.(2005)method was validated using well documented field studies,chosen to cover widely varying climatic and soil conditions,that are located in USA and Saudi Arabia.Two sites,i.e.Amarillo test site and College Station test site,located in Texas,USA,were selected to represent a 3D problem(Wray,1989).The College Station site and the Amarillo site properties are similar.The only exception is that the College Station site represents a wet climate while the Amarillo site was selected to represent a dry climate.SUCH model was used for the two sites to estimate soil suction changes throughout the soil mass and the vertical soil movement at monthly intervals over a period of 5 years(from August,1985 to July,1990).Al-Ghatt test site in Saudi Arabia(Dhowian et al.,1985)was also selected to represent a 2D problem,and was modeled over a period of 36 weeks.Comparisons were made between the estimated and the measured soil surface movements at several locations for the investigated field studies.For example,Fig.8 shows the predicted and measured monthly surface movements at 1.8 m outside slab edge along longitudinal axis for the Amarillo site.

The results of the SUCH model have shown moderate to good correlation with the reported field measurements of soil suction and the associated soil movements for the three sites(Wray et al.,2005).However,the application of the SUCH model to practical problems depends on the quantitative expression of the model parameters(i.e.the diffusion coefficient,the active zone depth,and the suction compression index)and the initial and boundary conditions.In SUCH model,the initial soil suction value information is required for each nodal point.For this reason,it is a challenge to reliably measure field suctions especially in expansive soils.Also,the results of the validation process revealed that Mitchell’s diffusion equation for soil suction(Eq.(30))needs to be modified to model the moisture movements in unsaturated fissured soils(soil cracks mechanism upon wetting).

4.2.Adem and Vanapalli(2013)method

Recently,Adem and Vanapalli(2013)proposed a simple method for predicting the vertical movements of unsaturated,expansive soils with respect to time.This method is referred to as modulus of elasticity based method(MEBM).The MEBM integrates Fredlund and Morgenstern(1976)constitutive equation for soil structure(Eq.(3))along with the soil-atmosphere model VADOSE/W(Geo-Slope,2007)to predict the variation of soil movement over time.The MEBM has been developed based on the assumption that the soil is an isotropic,linear elastic material,and the influence of the mechanical stress on the volume change of expansive soil underlying lightly loaded structures is insignificant and neglected.Hence,Eq.(3)was simplified for 1D problems and related the vertical movement of expansive soil with the matric suction changes and the associated modulus of elasticity.The total vertical soil movementΔh at any depth can be calculated by whereΔ(ua-uw)is the change in matric suction.

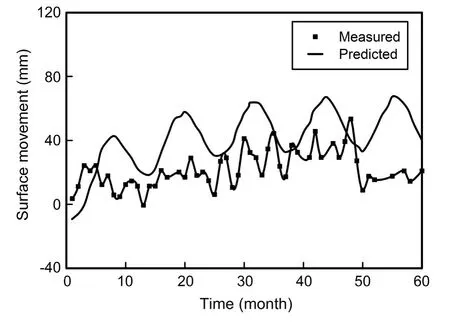
Fig.8.Predicted and measured monthly surface movements at 1.8 m outside slab edge along longitudinal axis at Amarillo site(modified after Wray et al.,2005).

Fig.10.The predicted heaves using Adem and Vanapalli(2013)method and the results of Vu and Fredlund(2004)under the center of the slab(modified after Adem and Vanapalli,2013).

Since it is necessary to define a value for Poisson’s ratio,Eq.(32)infers that the matric suction variations in the active zone depth and the associated modulus of elasticity are the key parameters to calculate the vertical soil movements(heave/shrink)over time.The matric suction variations within the active zone depth were estimated using the soil-atmosphere model VADOSE/W.Oh et al.(2009)proposed a semi-empirical model for coarse-grained soils for predicting the variation of modulus of elasticity with respect to matric suction using the SWCC as a tool.The semi-empirical model was proposed by extending similar concepts that were followed for the prediction of the shear strength(Vanapalli et al.,1996;Ye et al.,2010)and bearing capacity(Vanapalli and Mohamed,2007)of unsaturated soils.

Recently,Adem and Vanapalli(2015a)have extended this model for estimating the modulus for unsaturated expansive soils.The strength of this semi-empirical model lies in its use of conventional soil properties that include the SWCC and the soil modulus of elasticity under saturated condition Esat:where Eunsatis the elasticity modulus of soil under unsaturated conditions;Esatis the elasticity modulus of soil under saturated condition;S is the degree of saturation;and α,β are the fitting parameters.It was suggested thatα=0.05-0.15 andβ=2 provide reasonable modeling of the volume change behavior of expansive soils(Adem and Vanapalli,2015a).

Table 1Case studies modeled using the MEBM.

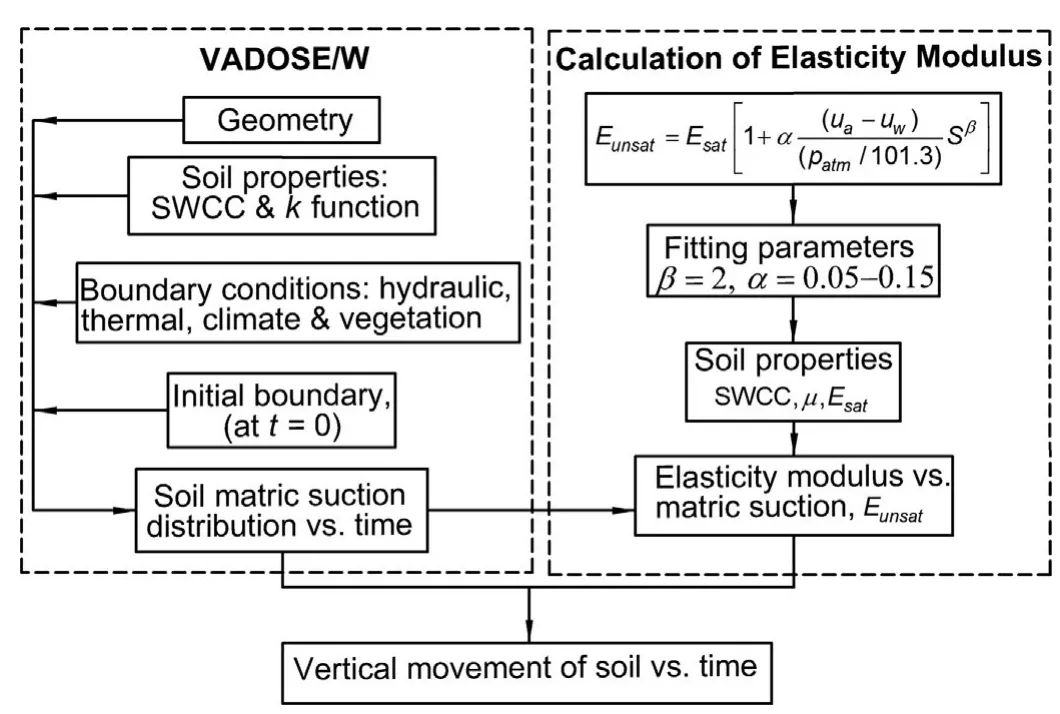
Fig.9.Flowchart for the step-by-step procedure of the MEBM.

Table 2Summary of the current methods for predicting the in situ volume change movement of expansive soils over time.

Once the matric suction variations within the active zone depth and the corresponding modulus of elasticity are determined,the soil movements can be estimated with respect to time using Eq.(32).Fig.9 shows the step-by-step procedure of the MEBM for predicting the vertical movements of unsaturated,expansive soils with respect to time.Table 1 summarizes four case studies from different regions in Canada and China that were used for testing the validity of the MEBM for the prediction of soil movement over time.These case studies were chosen to be representative of a variety of site conditions.The modeling details of these case studies using the MEBM are available in Vanapalli and Adem(2012,2013),Adem and Vanapalli(2013,2015b).Comparisons were provided between the results from the MEBM and the published results for the investigated case studies.For example,Fig.10 shows reasonable comparisons between the predicted heaves using the proposed MEBM and the heaves published in Vu and Fredlund(2004)for a light industrial building in Regina,Saskatchewan,Canada(Vanapalli and Adem,2013).

The MEBM is a relatively simple and promising method that can be used in engineering practice for predicting the long-term vertical movements of unsaturated expansive soils considering all the environmental factors.These predictions can be made using only the initial matric suction/water content data and the results from fairly routine geotechnical laboratory tests.However,the MEBM is uncoupled analysis where only the influence of matric suction variation on the volume change of unsaturated expansive soils is considered.In addition,the semi-empirical model(Eq.(33))was used to obtain the unsaturated modulus of elasticityas a function of only the matric suction,neglecting the influence of mechanical stress changes.However,to conduct a reliable estimation of the soil movements,it is often desirable to effectively describe the soil modulus of elasticity as a function of its influencing parameters.Adem and Vanapalli(2014)successfully used the dimensional analysis to propose a dimensionless model for estimating the modulus of elasticity of unsaturated expansive soils.The state of hydration of soil expressed in terms of the matric suction and the degree of saturation,the level of compaction and the confinement described by the initial void ratio and the confining stress,respectively,are considered to form the dimensionless parameters towards reliably estimating the soil modulus of elasticity.Validation of the dimensionless model was conducted using the experimental results of triaxial shear tests for different expansive soils.The semi-empirical model(Eq.(33))can be reliably used in practice for pavements and lightly loaded residential structures.However,the proposed dimensionless model can be used for all scenarios of loading conditions(both lightly and heavilyloaded structures)with a greater degree of confidence for estimating the modulus of elasticity of unsaturated expansive soils.

5.Conclusions

State-of-the-art of methods for predicting the vertical movements of unsaturated expansive soils subjected to environmental changes over time is reviewed in this paper.The prediction methods that are available in the literature are classified into three main categories,i.e.consolidation theory-based methods,water content-based methods,and suction-based methods.These methods are critically reviewed in terms of their predictive capacity in association with their strengths and limitations to assist the practicing engineers.Table 2 summarizes the key information of the methods.The review presented in this paper highlights the need for simple and efficient methods that can be easily used in conventional engineering practice to reliably predict the expansive soil movements with respect to environmental changes over time.

Conflict of interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Acknowledgment

The first author gratefully acknowledges her appreciation to the Libyan ministry of higher education and scientific research,which funded her PhD research program.The second author thanks the support from NSERC for his research programs.

Abed AA.Numerical simulation of a trial wall on expansive soil in Sudan.Plaxis Bulletin 2007;No.21:14-8.

Abed AA.Numerical modeling of expansive soil behavior[PhD Thesis].Stuttgart,Germany:Stuttgart University;2008.

Adem HH,Vanapalli SK.Elasticity moduli of expansive soils from dimensional analysis.Geotechnical Research 2014;1(2):60-72.

Adem HH,Vanapalli SK.Prediction of the modulus of elasticity of compacted unsaturated expansive soils.International Journal of Geotechnical Engineering 2015.http://dx.doi.org/10.1179/1939787914Y.0000000050[in press].

Adem HH,Vanapalli SK.Soil-environment interactions modeling for expansive soils. Environmental Geotechnics 2015. http://dx.doi.org/10.1680/envgeo.13.00089[in press].

Adem HH,Vanapalli SK.Constitutive modeling approach for estimating the 1-D heave with respect to time for expansive soils.International Journal of Geotechnical Engineering 2013;7(2):199-204.

Aitchison GD,Martin R.A membrane oedometer for complex stress-path studies in expansive clays.In:Proceedings of the 3rd international conference on expansive soils,Haifa.Jerusalem:Jerusalem Academic Press;1973.p.83-8.

Aitchison GD,Woodburn JA.Soil suction in foundation design.In:Proceedings of the 7th international conference on soil mechanics and foundation engineering,Mexico City;1969.p.1-8.

Alonso EE,Gens A,Josa A.A constitutive model for partially saturated soils.Géotechnique 1990;40(3):405-30.

Alonso EE,Gens A,Hight DW.Special problem soils.In:Proceedings of the 9th European conference on soil mechanics and foundation engineering,Dublin;1987.p.1087-146.

Alonso EE,Vaunat J,Gens A.Modeling the mechanical behavior of expansive clays.Engineering Geology 1999;54(1-2):173-83.

Barden L,Madedor AO,Sides GR.Volume change characteristics of unsaturated clay.Journal of the Soil Mechanics and Foundation Division,ASCE 1969;95:33-52.

Biot MA.General theory for three-dimensional consolidation.Journal of Applied Physics 1941;12(2):155-64.

Blatz JA,Graham J.Elastic-plastic modeling of unsaturated soil using results from a new triaxial test with controlled suction.Géotechnique 2003;53(1):113-22.

Bolzon G,Schre fler BA,Zeinkiewicz OC.Elastoplastic soil constitutive laws generalised to partially saturated states.Géotechnique 1996;46(2):279-89.

Bratton WL.Parameters for predicting shrink/heave beneath slab-on-ground foundations over expansive clays[PhD Thesis].Lubbock,Texas,USA:Texas Tech University;1991.

Briaud JL,Zhang X,Moon S.The shrink test-water content method for shrink and swell prediction.Journal of Geotechnical and Geoenvironmental Engineering 2003;129(7):590-600.

Brinkgreve RBJ,Al-Khoury R,Van Esch J.PLAXFLOW user manual.Rotterdam,the Netherlands:A.A.Balkema;2003.

Brackley IJA.Partial collapse in unsaturated expansive clay.In:Proceedings of the 5th regional conference for Africa on soil mechanics foundation and engineering,Luanda,Angola;1971.p.23-30.

Coleman JD.Stress/strain relations forpartly saturated soils.Géotechnique 1962;12(4):348-50.

Chao KC,Overton DD,Nelson JD.The effects of site conditions on the predicted time rate of heave.In:Proceedings of the unsaturated soils conference.Reston,Virginia,USA:American Society of Civil Engineers;2006.p.2086-97.

Chiu CF,Ng CWW.A state-dependent elastoplastic model for saturated and unsaturated soils.Géotechnique 2003;53(9):809-29.

Cui YJ,Delage P,Sultan N.An elastoplastic model for compacted soils.In:Proceedings of the 1st international conference on unsaturated soils,UNSAT-95,Paris.Rotterdam,the Netherlands:A.A.Balkema;1995.p.703-9.

Dakshanamurthy V,Fredlund DG.Moisture and air flow in an unsaturated soil.In:Proceedings of the 4th international conference on expansive soils.Reston,Virginia,USA:American Society of Civil Engineers;1980.p.514-32.

Dakshanamurthy V, Fredlund DG, Rahardjo H. Coupled three-dimensional consolidation theory of unsaturated porous media.In:Proceedings of the 5th international conference on expansive soils,Adelaide,South Australia;1984.p.99-104.

Delage P,Graham J.Mechanical behavior of unsaturated soils:understanding the behavior of unsaturated soils requires reliable conceptual models.In:Proceedings of the 1st international conference on unsaturated soils,UNSAT-95,Paris.Rotterdam,the Netherlands:A.A.Balkema;1995.p.1223-56.

Dhowian AW,Erol O,Youssef AF.Evaluation of expansive soils and foundation methodology in the Kingdom of Saudi Arabia.Research Report No.AT-5-88-3,CANCST.1985.

Fredlund DG.An introduction to unsaturated soil mechanics.In:Unsaturated soil engineering practice,geotechnical special publication.Reston,Virginia,USA:American Society of Civil Engineers;1997.p.1-37.

Fredlund DG,Hasan JU.One-dimensional consolidation theory:unsaturated soils.Canadian Geotechnical Journal 1979;16(3):521-31.

Fredlund DG,Morgenstern NR.Constitutive relations for volume change in unsaturated soils.Canadian Geotechnical Journal 1976;13(3):261-76.

Fredlund DG,Morgenstern NR.Stress state variables for unsaturated soils.Journal of Geotechnical Engineering Division,ASCE 1977;103(GT5):447-66.

Fredlund DG,Rahardjo H.Soil mechanics for unsaturated soil.New York,USA:John Wiley&Son,Inc.;1993.

Fredlund DG,Vu HQ.Prediction of volume change in an expansive soil as a result of vegetation and environmental changes.In:Geotechnical Special Publication,vol.115.Reston,Virginia,USA:American Society of Civil Engineers;2001.p.24-43.

Freeze RA,Cherry JA.Groundwater.Englewood Cliffs,New Jersey,USA:Prentice-Hall Inc.;1979.

Gens A,Alonso EE.A framework for the behavior of unsaturated expansive clays.Canadian Geotechnical Journal 1992;29(6):1013-32.

Geo-Slope.GEO-STUDIO VADOSE/W software package for seepage analysis,Version 6.16.Calgary,Alberta,Canada:Geo-Slope International Ltd.;2005.

Geo-Slope.Vadose zone modeling with VADOSE/W 2007:an engineering methodology.3rd ed.Calgary,Alberta,Canada:Geo-Slope International Ltd.;2007.Ito M,Hu Y.Prediction of the behavior of expansive soils.In:Proceedings of the 2011 Pan-Am CGS conference,Toronto,Ontario;2011.p.1-8.

Jones LD,Jefferson I.Expansive soils.In:Burland J,editor.ICE manual of geotechnical engineering,Vol.1:geotechnical engineering principles,problematic soils and site investigation.London,UK:ICE Publishing;2012.

Karube D.New concept of effective stress in unsaturated soil and its proving test.In:Donaghe RT,Chaney RC,Silver ML,editors.Proceedings of the advanced triaxial testing of soil and rock.West Conshohocken,Pennsylvania,USA:American Society for Testing and Materials;1988.p.539-52.

Kato S,Matsuoka H,Sun DA.A constitutive model for unsaturated soil based on extended SMP.In:Proceedings of the 1st international conference on unsaturated soils,UNSAT-95,Paris.Rotterdam,the Netherlands:A.A.Balkema;1995.p.739-44.

Kohgo Y,Nakano M,Miyazaki T.Theoretical aspects of constitutive modeling for unsaturated soils.Soils and Foundations 1993;33(4):49-63.

Lloret A,Alonso EE.Consolidation of unsaturated soils including swelling and collapse behavior.Géotechnique 1980;30(4):449-77.

Lloret A,Gens A,Batlle F,Alonso EE.Flow and deformation analysis of partially saturated soils.In:Hanrahan ET,Orr TLL,Widdis TF,editors.Proceedings of the 9th European conference on soil mechanics and foundation engineering,Dublin.Rotterdam,the Netherlands:A.A.Balkema;1987.p.565-8.

Lytton RL.Prediction of movement in expansive clays.In:The settlement’94 conference,College Station,Texas,geotechnical special publication,ASCE.Reston,Virginia,USA:American Society of Civil Engineers;1994.p.1827-45.

Lytton RL,Kher RK.Prediction of moisture movement in expansive clays.Research Report No.118-3.Austin,Texas,USA:Center for Highway Research,University of Texas at Arlington;1970.

Marr SA,Gilbert RB,Rauch AF.A practical method for predicting expansive soil behavior.In:Geotechnical special publication,ASCE.Reston,Virginia,USA:American Society of Civil Engineers;2004.p.1144-52.

Matyas EL,Radhakrishna HS.Volume change characteristics of partially saturated soils.Géotechnique 1968;18(4):432-48.

McKeen RG.Field studies of airport pavements on expansive clay.In:Proceedings of the 4th international conference on expansive soils,Denver;1980.p.242-61.McKeen RG,Johnson LD.Climate-controlled soil design parameters for mat foundations.Journal of Geotechnical Engineering 1990;116(7):1073-94.

Mitchell PW.The structural analysis of footings on expansive soil.Research Report No.1.Adelaide,Australia:Kenneth W.G.Smith and Associates;1979.

Modaressi A,Abou-Bekr N.Constitutive model for unsaturated soils:validation on a silty material.In:Proceedings of numerical methods in geotechnical engineering,Manchester;1994.p.91-6.

Nelson JD,Chao KC.Relationship between swelling pressures determined by constant volume and consolidation-swell oedometer tests.In:Khalili N,Russell AR,Khoshghalb,editors.Proceedings of unsaturated soils:research&applications,Sydney,Australia.London,UK:Taylor and Francis Group;2014.p.891-6.

Nelson JD,Miller DJ.Expansive soils:problems and practice in foundation and pavement engineering.New York,USA:Wiley;1992.

Nelson JD,Chao KC,Overton DD.De finition of expansion potential for expansive soil.In:Proceedings of the 3rd Asian conference on unsaturated soils,Nanjing,China.Beijing,China:Science Press;2007.p.1-6.

Nelson JD,Reichler DK,Cumbers JM.Parameters for heave prediction by oedometer tests.In:Proceedings of the 4th international conference on unsaturated soils,Carefree,Arizona.Reston,Virginia,USA:American Society of Civil Engineers;2006.p.951-61.

Nelson JD,Chao KC,Overton DD,Schaut RW.Calculation of heave of deep pier foundations.SEAGS and AGSSEA Geotechnical Engineering Journal 2012;43(1):12-25.

Ng CWW,Zhan LT,Bao CG,Fredlund DG,Gong BW.Performance of an unsaturated expansive soil slope subjected to artificial rainfall in filtration.Géotechnique 2003;53(2):143-57.

Oh WT,Vanapalli SK,Puppala AJ.Semi-empirical model for the prediction of modulus of elasticity for unsaturated soils.Canadian Geotechnical Journal 2009;46(8):903-14.

Overton DD,Chao KC,Nelson JD.Time rate of heave prediction for expansive soils.In:Proceedings of the GeoCongress 2006,Atlanta,Georgia.Reston,Virginia,USA:American Society of Civil Engineers;2006.p.1-6.

Pereira JHF.Numerical analysis of the mechanical behavior of collapsing earth dams during first reservoir filling[PhD Thesis].Saskatchewan,Saskatoon,Canada:University of Saskatchewan;1996.

Pufahl DE,Lytton RL.Temperature and suction profiles beneath highway pavements:computed and measured.In:Transportation research record 1307.Washington,D.C.,USA:Transportation Research Board;1992.p.268-76.

Rao BH,Venkataramana K,Singh DN.Studies on the determination of swelling properties of soils from suction measurements.Canadian Geotechnical Journal 2011;48(3):375-87.

Richards BG.Measurement of the free energy of soil moisture by the psychrometric technique using thermistors.In:Aitchison GD,editor.Proceedings of the symposium on moisture equilibria and moisture changes in soils beneath covered areas.Sydney,Australia:Butterworths;1965.p.39-46.

Richards BG.Behavior of unsaturated soils.In:Lee IK,editor.Soil mechanics-new horizons.New York,USA:Elsevier;1974.p.112-57[chapter 4].

Saeed IMA.Evaluation of improvement techniques for strip foundation on expansive clay soils in Gezira[PhD Thesis].Khartoum,Sudan:University of Khartoum;2004.

Sheng D,Fredlund DG,Gens A.A new modeling approach for unsaturated soils using independent stress variables.Canadian Geotechnical Journal 2008;45(4):511-34.

Tamagnini R.An extended Cam-clay model for unsaturated soils with hydraulic hysteresis.Géotechnique 2004;54(3):223-8.

Terzaghi K.The shear resistance of saturated soils.In:Proceedings of the 1st international conference on soil mechanics and foundation engineering,Cambridge,MA;1936.p.54-6.

Terzaghi K.Theoretical soil mechanics.New York,USA:Wiley;1943.

Thomas HR,He Y.Modeling the behavior of unsaturated soil using an elastoplastic constitutive model.Géotechnique 1998;48(5):589-603.

Thu TM,Rahardjo H,Leong EC.Elastoplastic model for unsaturated soil with the incorporation of soil-water characteristic curve.Canadian Geotechnical Journal 2007;44(1):67-77.

Vanapalli SK,Adem HH.Estimation of the 1-D heave in expansive soils using the stress state variables approach for unsaturated soils.In:Proceedings of the 4th international conference on problematic soils,Wuhan,China;2012.p.1-15.

Vanapalli SK,Adem HH.Estimation of the 1-D heave of a natural expansive soil deposit with a light structure using the modulus of elasticity based method.In:Proceedings of the 1st Pan-American conference on unsaturated soils,Colombia.London,UK:CRC Press;2013.p.1-14.

Vanapalli SK,Mohamed FMO.Bearing capacity of model footings in unsaturated soils.In:Proceedings of the experimental unsaturated soil mechanics.Berlin,Germany:Springer-Verlag;2007.p.483-93.

Vanapalli SK,Lu L.A state-of-the art review of 1-D heave prediction methods for expansive soils.International Journal of Geotechnical Engineering 2012;6(1):15-41.

Vanapalli SK,Fredlund DG,Pufahl DE,Clifton AW.Model for the prediction of shear strength with respect to soilsuction.Canadian Geotechnical Journal 1996;33(3):379-92.

Vu HQ,Fredlund DG.Using volume change indices for two-dimensional swelling analysis.In:Proceedings of the 55th Canadian geotechnical and 3rd joint IAHCNC and CGS groundwater specialty conferences,Niagara Falls,Ontario,Canada;2002.p.505-11.

Vu HQ,Fredlund DG.The prediction of one-,two-,and three-dimensional heave in expansive soils.Canadian Geotechnical Journal 2004;41(4):713-37.

Vu HQ,Fredlund DG.Challenges to modeling heave in expansive soils.Canadian Geotechnical Journal 2006;43(12):1249-72.

Vermeer PA,Brinkgreve R.PLAXIS finite element code for soil and rock analysis.Rotterdam,the Netherlands:A.A.Balkema;1995.

Wheeler SJ,Karube D.Constitutive modeling.In:Alonso EE,Delage P,editors.Proceedings of the 1st international conference on unsaturated soils.Rotterdam,the Netherlands:A.A.Balkema;1996.p.1323-56.

Wheeler SJ,Sharma RJ,Buisson MSR.Coupling of hydraulic hysteresis and stress strain behavior in unsaturated soils.Géotechnique 2003;53(1):41-54.

Wheeler SJ,Sivakumar V.An elastoplastic critical state framework for unsaturated soil.Géotechnique 1995;45(1):35-53.

Wong TT,Fredlund DG,Krahn J.A numerical study of coupled consolidation in unsaturated soils.Canadian Geotechnical Journal 1998;35(6):926-37.

Wray WK.Final Report.Mitigation of damage to structures supported on expansive soils,vol.1.Washington,D.C.,USA:National Science Foundation;1989.

Wray WK.Using soil suction to estimate differential soil shrink or heave.In:Unsaturated soil engineering practice,geotechnical special publication 68.Reston,Virginia,USA:American Society of Civil Engineers;1997.p.66-87.

Wray WK.Mass transfer in unsaturated soils:a review of theory and practices.In:Proceedings of the 2nd international conference on unsaturated soils,Beijing;1998.p.99-155.

Wray WK,El-Garhy BM,Youssef AA.Three-dimensional model for moisture and volume changes prediction in expansive soils.Journal of Geotechnical and Geoenvironmental Engineering 2005;131(3):311-24.

Ye W,Zhang Y,Chen B,Zhou X,Xie Q.Shear strength of an unsaturated weakly expansive soil.Journal of Rock Mechanics and Geotechnical Engineering 2010;2(2):155-61.

Yoshida RT,Fredlund DG,Hamilton JJ.The prediction of total heave of a slab-ongrade floor on Regina clay.Canadian Geotechnical Journal 1983;20(1):69-81.

Zhang X.Consolidation theories for saturated-unsaturated soils and numerical simulations of residential buildings on expansive soils[PhD Thesis].College Station,Texas,USA:Texas A&M University;2004.

Zhang X,Lytton RL,Briaud JL.Coupled consolidation theory for saturated unsaturated soils.In:Proceedings of the 3rd biot conference on poromechanics(Biot Centennial).Norman,Oklahoma,USA:University of Oklahoma;2005.p.323-30.