优化权重下平稳高斯序列的部分和与最大值的几乎处处中心极限定理

汪园芳，吴群英

（桂林理工大学理学院，广西 桂林 541004）

0 引言及定义

独立同分布的随机变量序列的部分和形式的几乎处处中心极限定理被Brosamler［1]和Schatte［2]首次引入并证明，其一般形式为：设X1,X2,…,Xn是一组独立同分布的随机变量序列，令和是常数数列，如果满足为分布函数，则对于G的任意连续点x都有

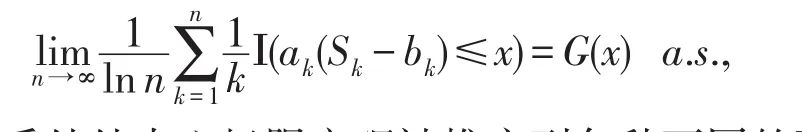
其中，Ⅰ(·)为示性函数.之后，几乎处处中心极限定理被推广到各种不同的形式.Fahrner［3]和Stadtmuller［3]以及Cheng［4]将部分和形式的几乎处处中心极限定理推广到最大值形式的几乎处处中心极限定理，其一般形式为：设X1,X2,…,Xn是一组独立同分布的随机变量序列，令和是常数数列，

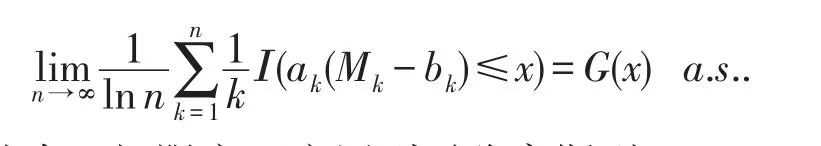
随后，Csaki等［5]将几乎处处中心极限定理应用到平稳高斯列，Dudzinski［6]将部分和形式的几乎处处中心极限定理推广到部分和与最大值的形式，笔者在文献［6]的基础上将权重从推广到并且证明了该权重下的几乎处处中心极限定理.

本文中，记X1,X2,…,Xn为平稳的高斯序列为示性函数为标准正态分布函数.an～bn表示当表示当n→∞时，存在c＞0使an≤cbn.

1 主要结果

定理设为平稳高斯序列，如果为正的慢变化函数，并且常数列满足存在0≤τ＜∞，使则有：对∀x,y∈ℝ,

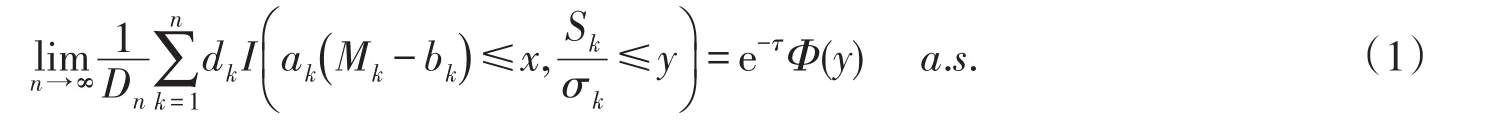
注1：对于dk有（1）式成立，则对满足（1）式也成立.

注2：当β=0时，Dudzinski证明出的定理结果是本文中定理的一个特例.

2 几个引理

引理1［7]设ξ1,ξ2,…为一组有界的随机变量序列，如果存在某ε＞0,使得引理2［6]在满足定理的情况下，对任意的x,y∈ℝ，存在γ＞0，当m＜n时有：

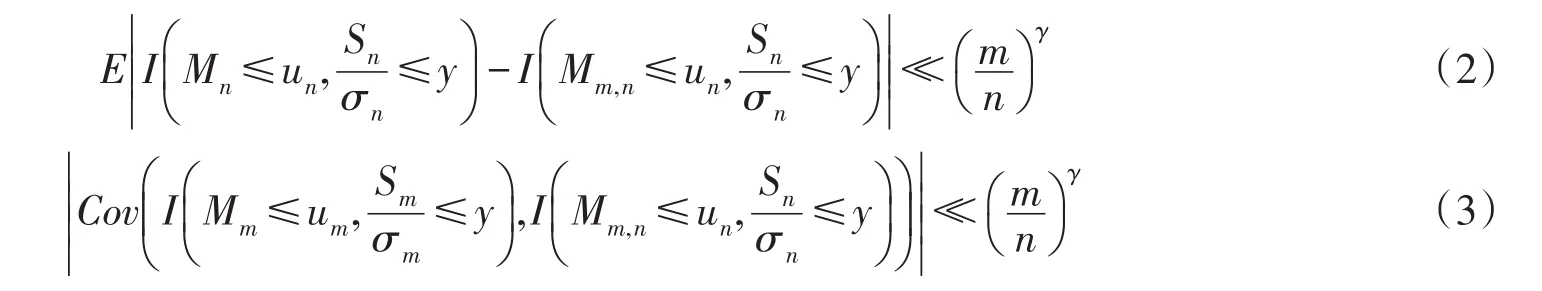
引理3［8]（正态比较引理） 设{ }Xn,n≥1是平稳高斯序列，rij=Cov(Xi,Xj)，则对任意的实数ui,i=1,2,…,n,有

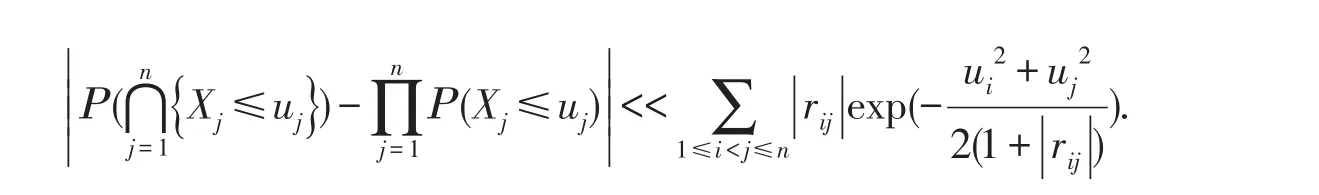
引理4［9]（Toeplitz引理） 设实数满足如果x=0并且实数阵列符合条件则有如果x≠0，则在上面的条件下，再加上这个条件，仍然有

3 定理的证明

变化函数，则对∀ε＞0，有当1≤i≤n时，则有

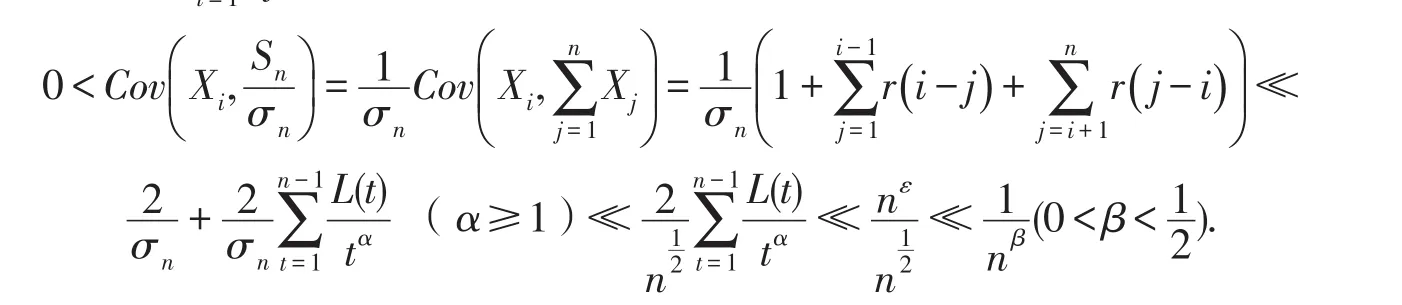
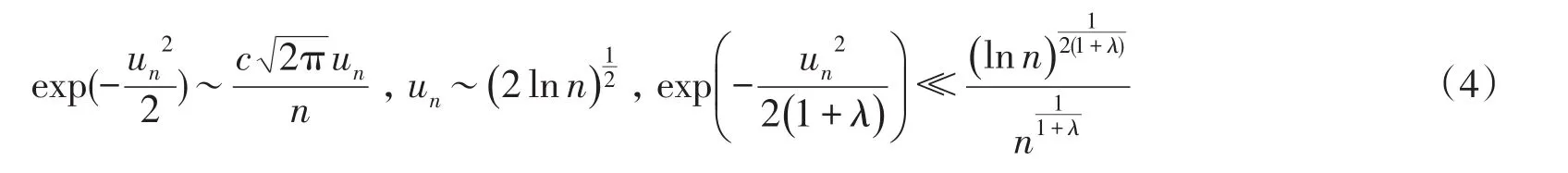
记Yn为一随机变量，与有相同的分布，且与( )X1,…,Xn独立，由引理 3及（4）式知，当时，则有

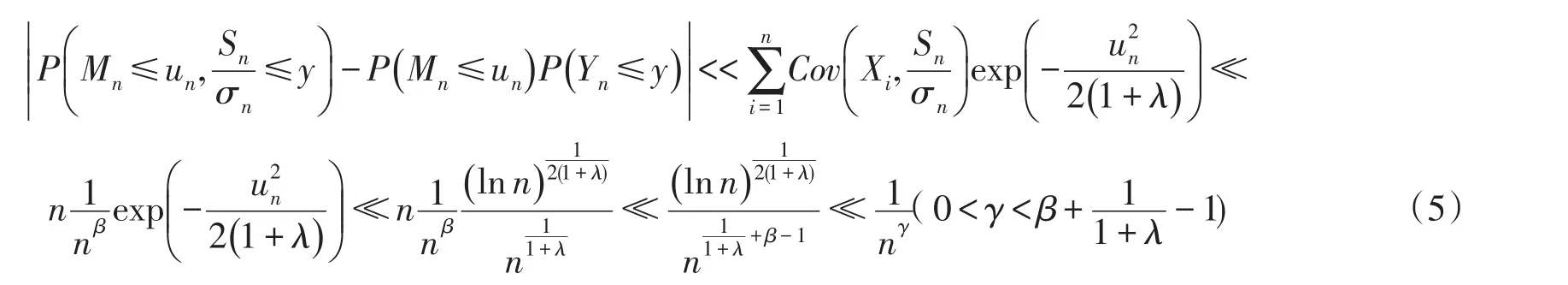
则由（5）式有：

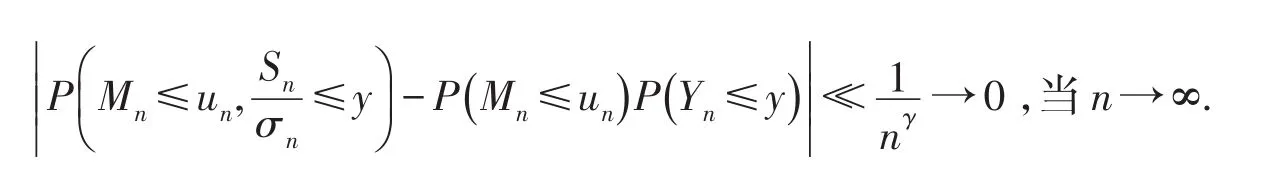
进一步地，再根据文献［8]有

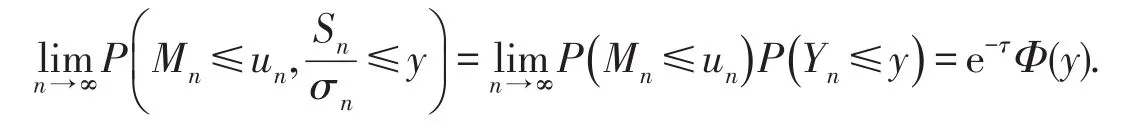
再由引理4有：

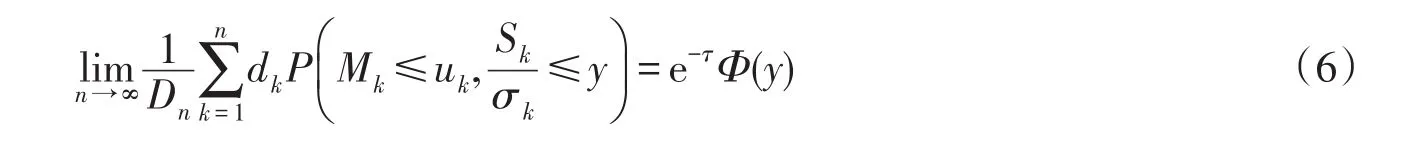
则要证明定理，只要证明

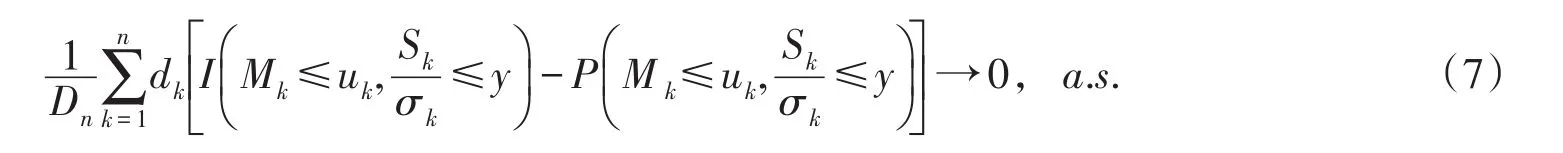
要证明（7）式，由引理1，只要证明存在某ε＞0,

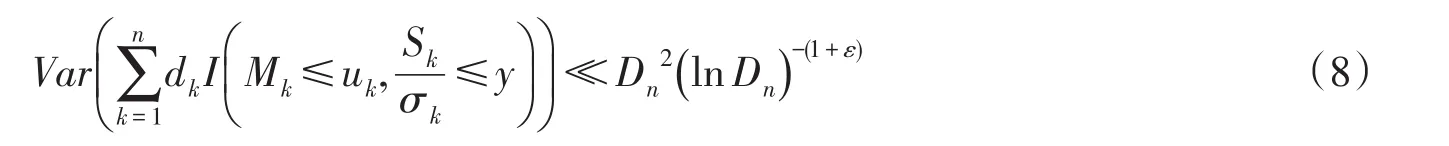
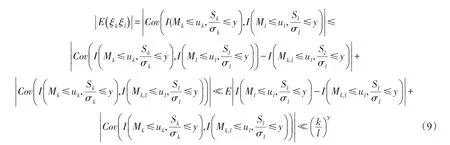
根据（9）式有

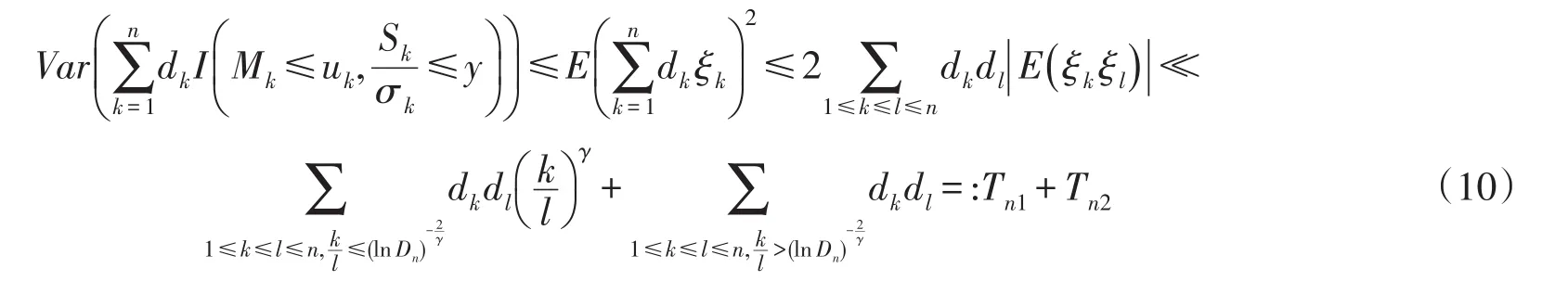
对于Tn1，有下面的估计：

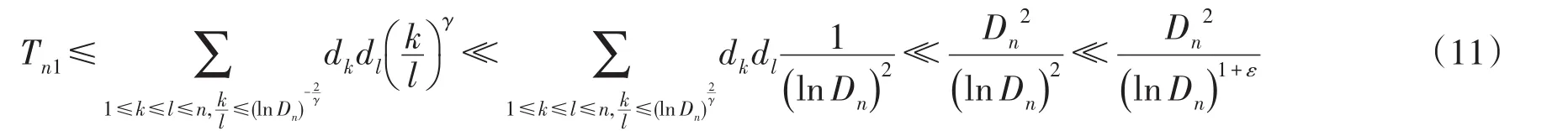
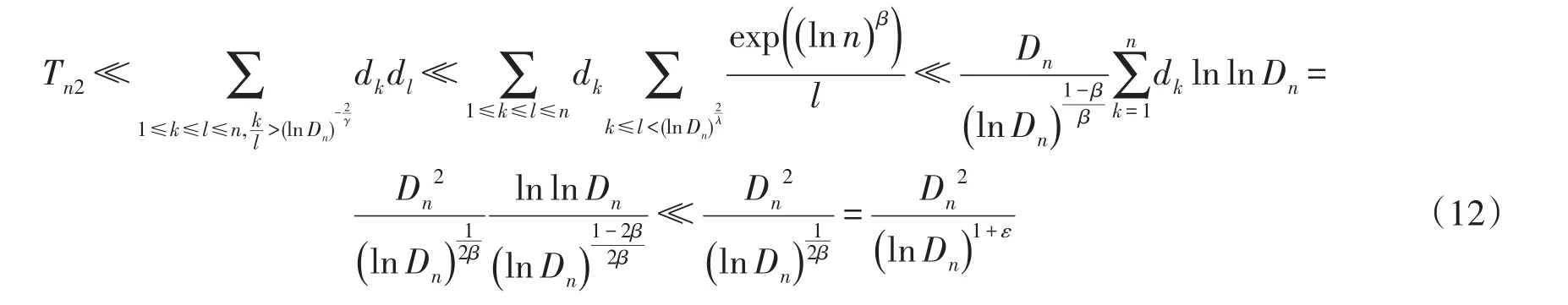
结合（10）～（12）式，证明了（8）式，则（7）式成立.最后由（6）式可知定理得证.

［1]Brosamler GA.An almoste very where central limit theorem［J].Math Proc Cambridge Philos Soc，1988，104:561-574.

［2]Schatte P.On strong versionsof the central limit theorem［J].Math Nachr，1988，137:249-256.

［3]Faharner I，Stadtmuller U.On almostsure centralmax-limit theorems［J].StatProbab Lett，1998，37:229-236.

［4]Cheng H，Peng L，QiYC.Almostsure convergence in extreme value theory［J].Math Nachr，1998，190:43-50.

［5]Csaki E，Gonchigdanzan K.Almostsure limit theorems for themaximum of stationary Gaussian Sequences［J].Statist Probab Lett，2002，58:195-203.

［6]Dudzinski M.The almost sure central limit theorems in the joint version for the maxima and sums of certain stationary Gaussian sequences［J].Statist Probab Lett，2008，78:347-357.

［7]WU Qunying.Almost sure central limit theory for products of sums of partial sums［J].Math Appl Chinese Univ，2012，27:169-180.

［8]Leadbetter M R，Lindgren G，Rootzen H.Extremes and related properties of random sequences and processes［M].New York:Springer，1983.

［9]吴群英.混合序列的概率极限理论［M].北京：科学出版社，2006.