一类三次多项式微分系统的相图
高静,刘娟
(1.广东白云学院基础教学部,广州 510450,2.广东财经大学数学与统计学院,广州 510320)
1 引言及主要结果
文献[1]中将系统

分为20类,其中一类为

其中b>0,研究系统(1)的原点O(0,0)是中心还是焦点的判别,并给出了中心的条件;还研究了当原点O(0,0)是中心,b=1时,系统的相图.
主要结果为以下定理:
定理1系统(1)有奇点O(0,0)且有以下结论:
1)当α+bγ>0时,O(0,0)为一阶不稳定细焦点;当α+bγ<0时,O(0,0)为一阶稳定细焦点.
2)当α+bγ=0但(α,γ)≠(0,0)时,若γ>0,则O(0,0)为二阶不稳定细焦点;若γ<0时,O(0,0)为二阶稳定细焦点.
3)当且仅当α=γ=0时,O(0,0)为中心.
定理2当原点O(0,0)是中心时,若b=1,系统(1)变为

则系统(2)的相图有3种,如图1.

图1 系统(2)的相图
2 定理1的证明
经非退化线性变换:
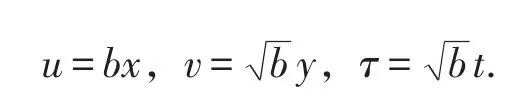
系统(1)化为

由文献[2]中给出的公式,奇点O(0,0)的前2阶焦点量为:
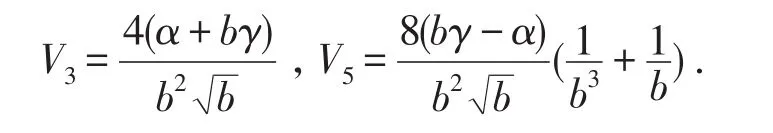
所以可以得到以下几种情况:
3)若V3=0且V5=0,即α=γ=0.所以当且仅当α=γ=0时,O(0,0)为中心.
3 定理2的证明
为了计算系统(2)的有限奇点[3-4],须求解方程组
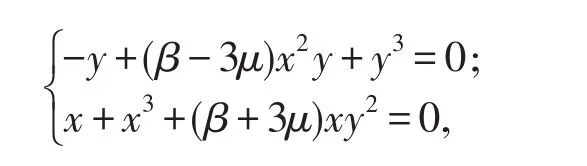
所以易算出系统有奇点O(0,0),A1(0,1),A2(0,-1).
当β2≠1+9μ2且1+9μ2-β2>0,β+3μ+1<0,β-3μ+1>0或1+9μ2-β2<0,β+3μ+1>0,β-3μ+1<0时还有奇点
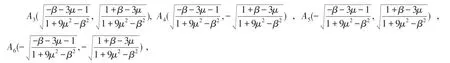
O(0,0)在任何情况下都是中心,后面的讨论中不再说明.
对于系统(2)有矩阵

所以奇点A1(0,1),A2(0,-1)对应矩阵均为其对应的特征方程为λ2=2(1+β+3μ),故当β+3μ>-1时,奇点A1(0,1),A2(0,-1)均为鞍点.
当β+3μ<-1时,奇点A1(0,1),A2(0,-1)一次近似为中心;当β+3μ=-1时,奇点A1(0,1),A2(0,-1)为高阶奇点.
当β+3μ=-1时,奇点A1(0,1),A2(0,-1)为高阶奇点,它们都属于相应的线性方程组的两个特征根都是零,但线性项系数不全为零.
对于奇点A1(0,1),令x1=x,y1=y-1,将原点移至A1(0,1),又注意到β=-3μ-1,并令2dt=dτ,则系统(2)化为

由y+P2(x,y)=0,解得隐函数

并有

同理可得,A2(0,-1)与A1(0,1)有相同的类型.
奇点A3,A6对应矩阵均为
若ak=-3μ>0即μ<0,则A1(0,1)为鞍点.
若ak=-3μ<0即μ>0;n=1,bn=-2(3μ+1)<0.
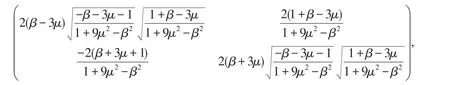
奇点A4,A5对应矩阵均为

通过计算它们的行列式均小于零,容易判断出A3,A4,A5,A6都为鞍点.
为了研究系统(2)无穷远处奇点的性态,要作Poincaré变换.


系统(4)在u轴(z=0)上有两个无穷远奇点
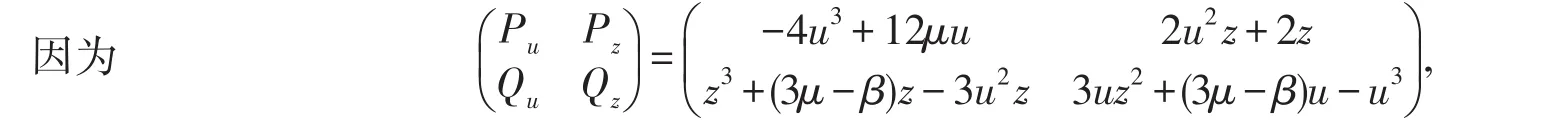

因此得到如下结论:
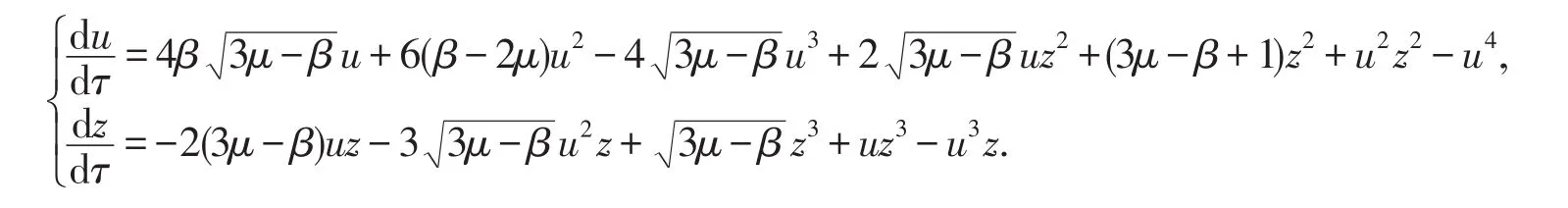
作变换(u,z)→(z,u),并除以4β3μ-β,上述系统化为
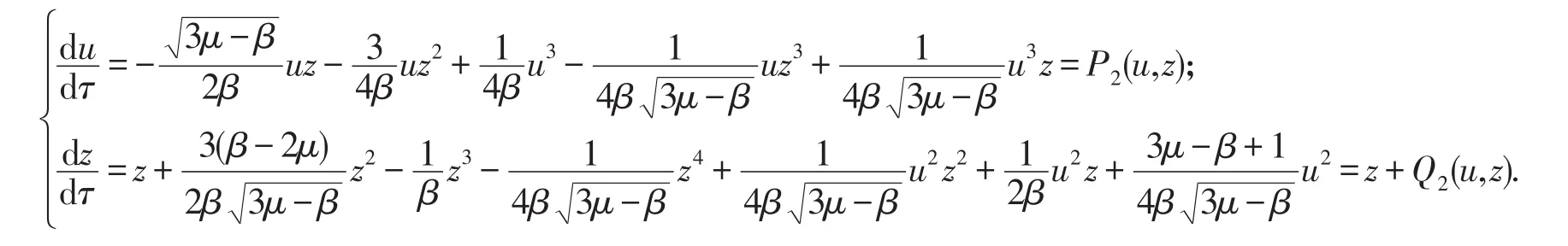
由z+Q2(u,z)=0,解得隐函数

并有
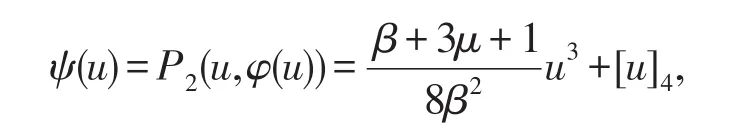
注意到4β3μ-β<0,此时奇点的稳定性恰好与系统(3)中的结论相反.于是有:
i)当β+3μ+1>0时是稳定结点.
iii)当β+3μ+1=0时,am=0,这种情况在后面的讨论并没有遇到,所以这里不在继续讨论.
同 理 可得:当β+3μ+1>0 时是 不 稳 定 结 点 ;当β+3μ+1<0 时 ,是鞍点;另外它的4条分界线分别沿方向和进入
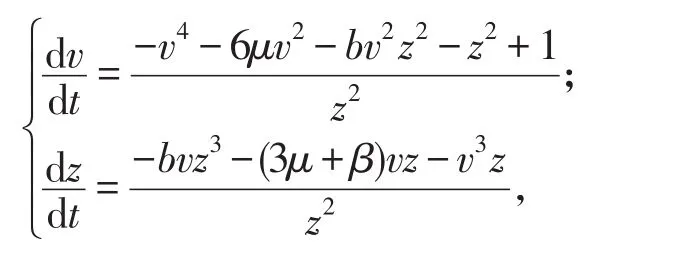

系统(5)在v-z平面的原点不是无穷远奇点.
注意到Z=0是系统(5)的解,故赤道由奇点和轨线连成.又因所以在Poincare圆盘上,在与B对应的奇点的轨线走向一致,在与C对应的奇点C′,C″的轨线走向一致.又因为对系统(2)有
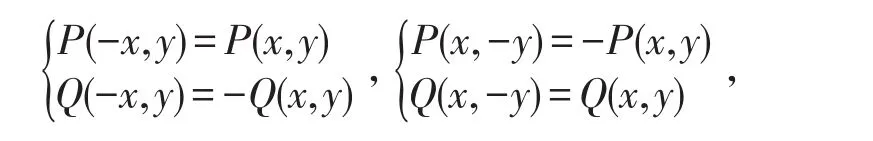
所以系统(2)关于x轴或y轴都对称,因而只要讨论第一象限的情况就可以了.
分两种情况讨论:

这时β=-1,μ=0,此时系统(2)变成
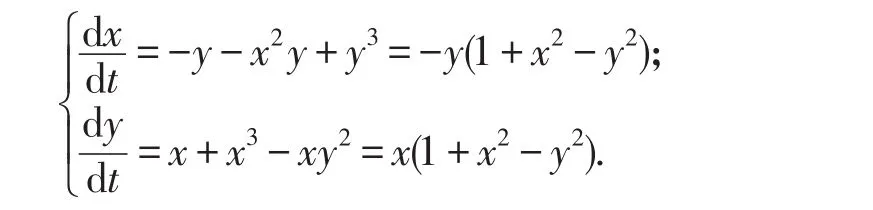
右端函数有公因子,故有无穷多个奇点在曲线y2-x2=1上,并且还有3个奇点O(0,0),A1(0,1),A2(0,-1).对于无穷远处,它在u轴上有两个无穷远点B(1,0),C(-1,0).这时A1(0,1),A2(0,-1),B(1,0),C(-1,0)都为高阶奇点.系统(2)有首次积分x2+y2=r2,r∈R.
根据以上分析,系统(2)的相图拓扑等价于图1(a).
这时系统(2)有首次积分:

积分因子
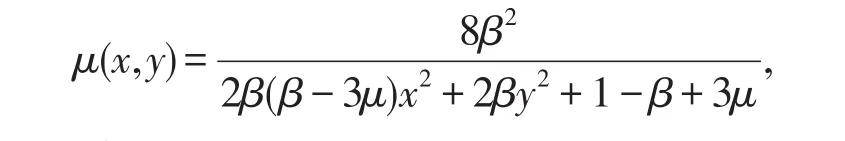
由文献[5]知,系统(2)在平面上不存在极限环,焦点和结点,它有3个奇点:O(0,0),A1(0,1),A2(0,-1).
分两种情况:
1)当β+3μ>-1时,奇点A1(0,1),A2(0,-1)均为鞍点;
2)当β+3μ<-1时,奇点A1(0,1),A2(0,-1)一次近似为中心,所以奇点A1(0,1),A2(0,-1)就是系统(2)的中心.
对于无穷远处,在u轴上有两个无穷远点
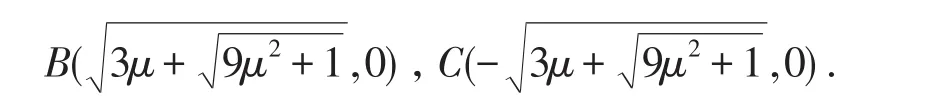
分两种情况:
B(为稳定结点为不稳定结点.
2)β=-9μ2+1.
当β+3μ>-1时为稳定结点为不稳定结点.
当β+3μ<-1时为鞍点,另外它的4条分界线分别沿方向和进入为鞍点,另外它的4条分界线分别沿方向和进入
综合以上分析,有两种情况:
1)当β+3μ>-1且时,都有A1(0,1),A2(0,-1)为鞍点为稳定结点,为不稳定结点.系统(2)的相图拓扑等价于图1(b).
2)当β+3μ<-1且时,这时所以这种情况是不成立的;
当β+3μ<-1且时,这时A1(0,1),A2(0,-1)为中心为鞍点.系统(2)的相图拓扑等价于图1(c).
系统(2)的奇点还有第三种情况
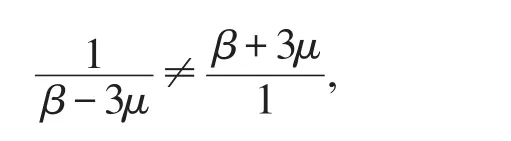
但较复杂,本文中没有涉及,这是努力的方向.
[1]Yang Xinan ,Zhang Jianfeng.Algebraic classification of polynomial systems in the plane[J].Ann of Diff Eqs,1990,6(4):463-480.
[2]刘一戎.一类平面三次系统的焦点量公式、中心条件与中心积分[J].科学通报,1986(2):85-87.
[3]张芷芬,丁同仁,黄文灶,等.微分方程定性理论[M].北京:科学出版社,2003.
[4]张锦炎,冯贝叶.常微分方程几何理论与分支问题[M].北京:北京大学出版社,2002.
[5]叶彦谦.极限环论[M].上海:上海科技出版社,1984.

