幂硬化对疲劳弹塑性弯曲裂纹塑性区的影响

杨大鹏，潘海洋，赵耀，李天匀

（1.郑州职业技术学院机械工程系，河南 郑州 450121；2.华中科技大学船舶与海洋工程学院，湖北 武汉 430074；3.郑州职业技术学院城市轨道交通系，河南 郑州 450121）①

0 引言

准静态轻微弯曲裂纹的摄动分析最早由Banichuk［1]、Goldstein和Salganik［2-3]完成.Cotterell和Rice［4]用同样方法得到了应力强度因子的简易表达式，研究了无限大平面中半无限裂纹的路径预测问题.Karihaloo等［5]、Sumi等［6-7]曾分别运用二阶、一阶摄动方法研究了无限大平面内受制于无穷远处多向拉应力的轻微弯曲裂纹的扩展问题.YoichiSumi等［8]已计算出任意远场边界条件、线弹性弯曲裂纹尖端应力强度因子的近似值.Wu［9]、Amestoy和Leblond［10]也求解出弯曲裂纹尖端应力强度因子与路径形状参数的近似解.

但是，关于弯曲裂纹扩展路径的研究均针对线弹性和理想塑性材料［11].关于疲劳载荷作用下幂硬化材料弹塑性弯曲裂纹的路径预测、硬化塑性区域内的应力场计算、硬化塑性区域范围的确定问题，科技工作者们至今尚少着手研究.在工程实际中，理想塑性材料并不存在，实际金属材料均具有幂硬化特性.因此，有必要研究幂硬化金属材料的断裂特性.本文中将运用二阶摄动方法对疲劳载荷作用下幂硬化材料弹塑性裂纹弯曲扩展问题进行研究，计算疲劳载荷作用下弯曲裂纹尖端硬化塑性区尺寸的最大值和变化幅值，从而更精确地服务于工程实际.

1 疲劳载荷作用下幂硬化材料弹塑性弯曲裂纹塑性区最大值和变化幅值的修正计算

1.1 弯曲裂纹尖端硬化塑性区边界应力状态分析由已有文献［12-16]可得弯曲裂纹尖端硬化塑性区边界应力的最大值为：σ1、σ2和σ3，其中n为材料的形变硬化指数，σs为材料的塑性屈服极限，σb为材料的抗拉强度，α、β、γ是弯曲裂纹形状参数，(KIP)max、(KIIP)max分别为硬化塑性区边界上的均布正应力σ1与剪应力σ2在假想弯曲裂纹尖端产生的I型、II型应力强度因子的最大值，ΔKIP、ΔKIIP分别为硬化塑性区边界上的均布正应力σ1与剪应力σ2在假想弯曲裂纹尖端产生的I型、II型应力强度因子的变化幅值，设kI与kII分别为I型、II型静态应力强度因子，T、bI与bII分别为准静态远场边界值决定的系数分别为弯曲裂纹尖端I型、II型应力强度因子的远区域渐进值分别表示弯曲裂纹尖端交变应力I型、II型强度因子的远区域渐进最大值，KI(f)、KII

(f)分别为弯曲裂纹尖端交变I型、II型应力强度因子的远区域渐进修正值分别表示弯曲裂纹尖端交变I型、II型应力强度因子的远区域渐进修正最大值.

式（3）、式（4）与式（5）中的负号表示弯曲裂纹尖端硬化塑性区边界上的正应力、剪应力的作用与外应力的作用是相反的.

硬化塑性区边界上的均布正应力σ1与剪应力σ2在假想弯曲裂纹尖端产生的I型、II型应力强度因子的最大值分别为（KIP）max、（KIIP）max，变化幅值分别为ΔKIP、ΔKIIP.于是，同理［14]可得：

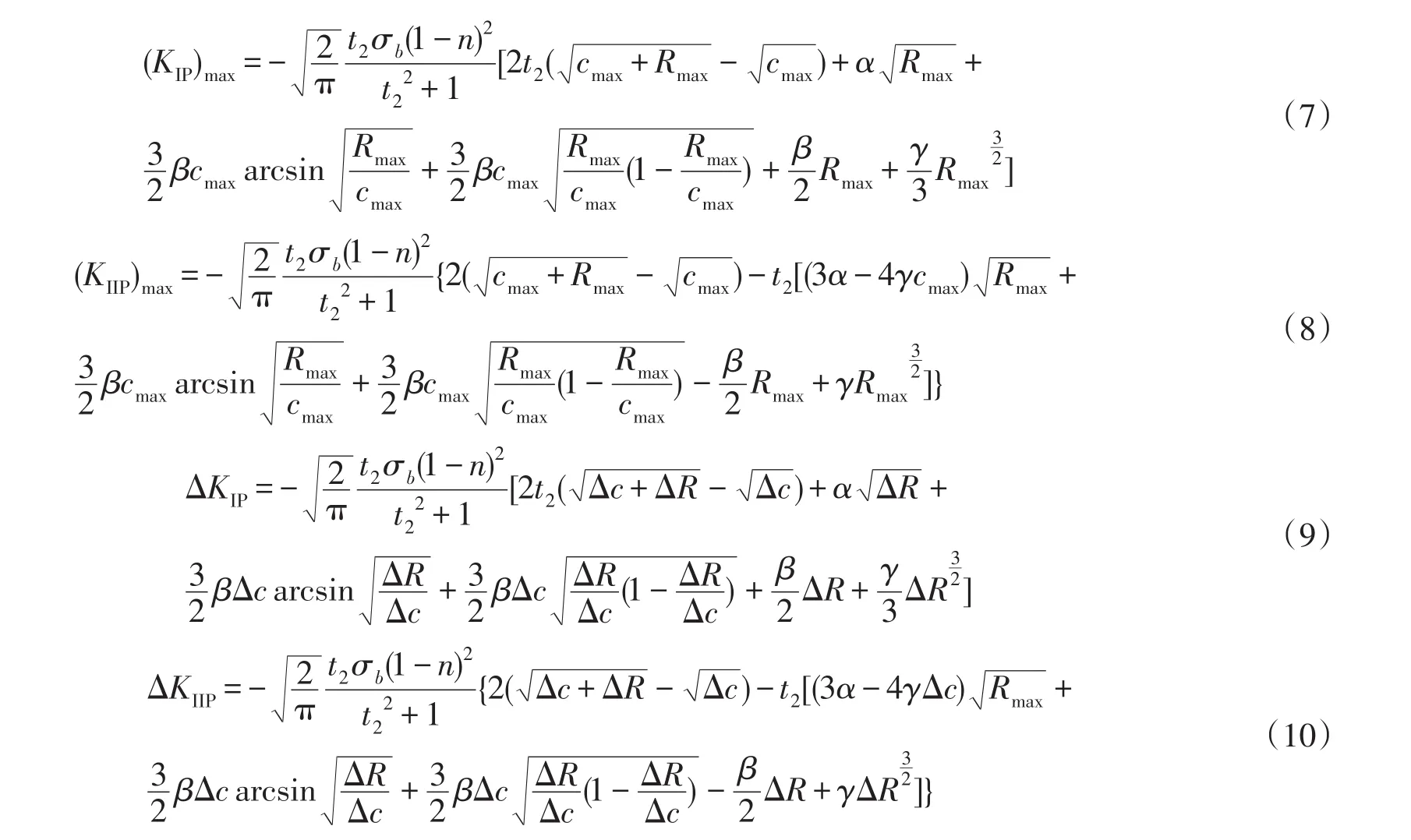
1.2 弯曲裂纹尖端硬化塑性区的最大值和变化幅值在裂纹直线部分延长线上投影长度的数值求解由文献［17]可得弯曲裂纹尖端硬化塑性区大小随疲劳载荷的增减而变化，外应力越大，塑性区越大，裂纹尖端硬化塑性区与弹性区循环交替变化.因为弯曲裂纹硬化塑性区的端点无奇异性，由文献［14]可得：

将式（7）、式（16）与式（17）代入式（11），再将式（9）、式（18）与式（19）代入式（12），并辅以式（15），用数值解法可以计算出弹塑性弯曲裂纹尖端硬化塑性区最大值和变化幅值在裂纹直线部分延长线上的投影长度.

1.3 弯曲裂纹尖端硬化塑性区最大值和变化幅值在裂纹直线部分延长线上投影长度的计算分析由文献［18]知：σ*=E(ε*)n，其中σ*为有效应力，ε*为有效应变.n为材料的硬化指数.对于一般金属材料，1 9≤n≤1 3.理想塑性材料的硬化指数为0，理想弹性材料的硬化指数为1.H是裂纹直线部分的长度，Rmax是弯曲裂纹尖端硬化塑性区最大值在裂纹直线部分延长线上的投影长度，ΔR是弯曲裂纹尖端硬化交变塑性区在裂纹直线部分延长线上的投影长度，a是弯曲裂纹在裂纹直线部分延长线上的投影长度，α0是弯曲裂纹的形状参数［22]，(σa)max是与裂纹直线部分垂直的外部作用应力的最大值，(σr)max是与裂纹直线部分平行的外部作用应力的最大值，σs是材料的屈服极限，E是材料的弹性杨氏模量.

基于弹塑性弯曲裂纹尖端硬化塑性区最大值和变化幅值在裂纹直线部分延长线上投影长度的数值解随弯曲裂纹形状参数的变化关系，分别作图如下：

图1 弯曲裂纹塑性区最大值投影长度随裂纹弯曲形状参数的变化关系

从图1可以看出，在同样外载荷作用下，相同的裂纹弯曲形状参数对应的弯曲裂纹塑性区最大值在裂纹直线部分延长线上的投影长度随着材料硬化指数不断增大而逐渐减小.具体减少的数量详见图1（a）到（e）.当n等速均匀增加时，硬化塑性区最大值的投影长度加速减少，减少的幅度越来越大.

从图2可以看出，在同样外载荷作用下，相同的裂纹弯曲形状参数对应的弯曲裂纹塑性区变化幅值在裂纹直线部分延长线上的投影长度随材料硬化指数不断增大而逐渐减小.当n等速均匀增加时，硬化塑性区变化幅值的投影长度加速减少，减少的幅度越来越大.还可以看出，当材料的硬化指数相同时，弯曲裂纹塑性区变化幅值在裂纹直线部分延长线上的投影长度随外载荷的不断减小而逐渐减小.

从图3可以看出，材料硬化指数越大，弯曲裂纹塑性区最大值于裂纹直线部分延长线上的投影长度随着外载荷的不断增大而增大的速度逐渐放慢.当硬化指数均匀增加时，弯曲裂纹塑性区最大值投影长度随着外载荷增大而增大的速度逐渐增加.

图2 弯曲裂纹塑性区变化幅值投影长度随裂纹弯曲形状参数的变化关系

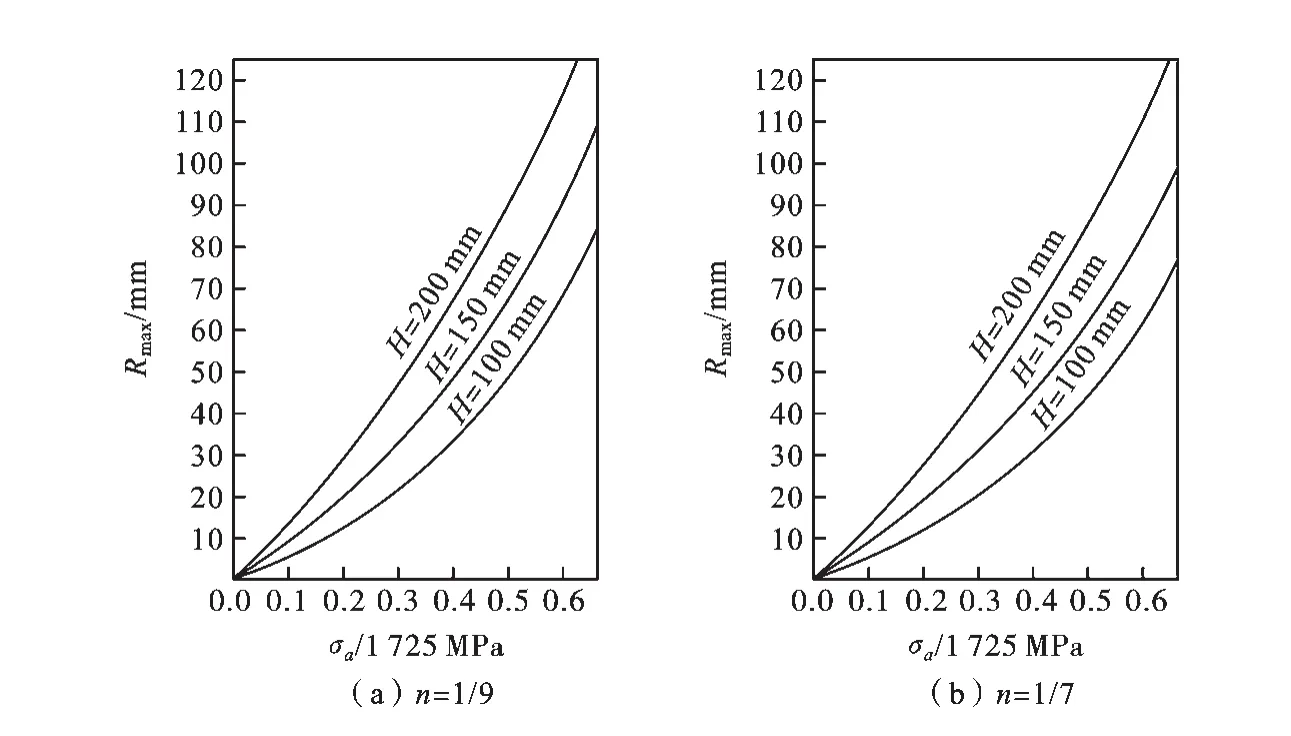
图3 弯曲裂纹塑性区尺寸最大值与外载荷之间的变化关系

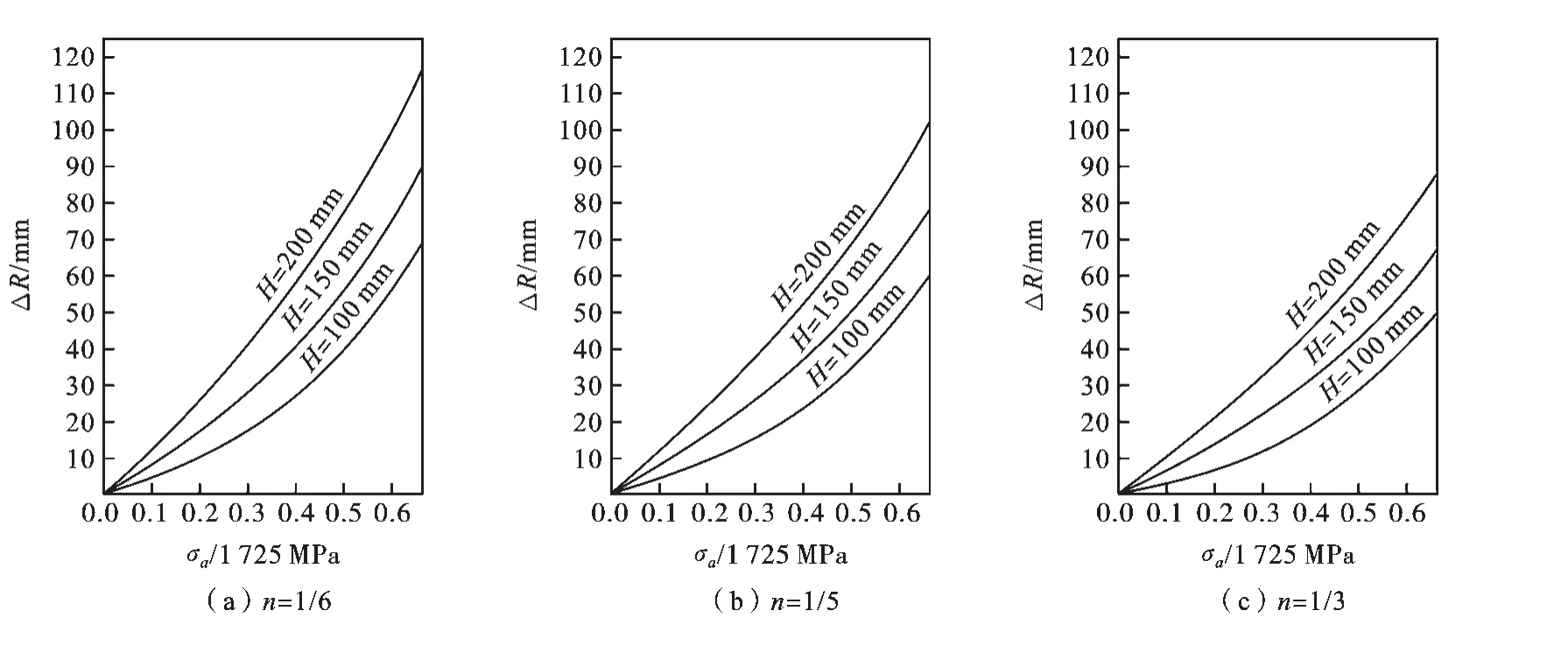
图4 弯曲裂纹塑性区尺寸变化幅值与外载荷之间的变化关系

从图4可以看出，材料硬化指数越大，弯曲裂纹塑性区变化幅值在裂纹直线部分延长线上的投影长度随着外载荷的不断增大而增大的速度逐渐放慢.当硬化指数均匀增加时，弯曲裂纹硬化塑性区变化幅值投影长度随着外载荷增大而增大的速度逐渐增加.

2 结论

1）计算得出疲劳载荷作用下弹塑性弯曲裂纹尖端硬化塑性区边界上任意一点的应力的最大值和变化幅值.

2）用数值解法计算得出弹塑性弯曲裂纹尖端硬化塑性区最大值和变化幅值在裂纹直线部分延长线上的投影长度，并作图分析硬化塑性区尺寸的最大值、变化幅值与材料硬化指数之间的变化关系.

3）弯曲裂纹尖端硬化塑性区最大值和变化幅值在裂纹直线部分延长线上的投影长度随材料硬化指数n的增大而减少，当n等速均匀增加时，硬化塑性区最大值和变化幅值的投影长度加速减少，减少的幅度越来越大.

［1]Banichuk N V.Determination of the form ofa curvilinear crack by smallpara meter technique［J].Izv，An SSSRMTT，1970，7（2）:130-137（in Russian）.

［2]Goldstein RV，Salganik R L.Plane problem of curvilinear cracks in an elastic solid［J].Izv，An SSSRMTT，1970，7（3）:69-82（in Russian）.

［3]Goldstein RV，Salganik R L.Brittle fracture of solids with arbitrary cracks［J].Int J Fracture，1974，10:507-523.

［4]Cotterell B，Rice JR.Slightly curved or kinked cracks［J].Int JFracture，1980，16:155-169.

［5]Karihaloo B L，Keer LM，NematN S，etal.Approximate description of crack Kinking and curving［J].JApplMech，1981，48:515-519.

［6]SumiY，Nemat-nasser S，Keer LM.On crack branching and curving in a finite body［J].Erratum，Int，JFracture，1984，24:159.

［7]Sumi Y.A note on the firstorder perturbation solution ofa straight crack with slightly branched and curved extension under a generalgeometric and loading condition［J].Engng Fracture Mech，1986，24:479-481.

［8]Yoichi Sumi，Member.A second order perturbation solution of a non-collinear crack and its application to crack path prediction ofbrittle fracture inweldment［J].JSNA Japan，1989，12:166.

［9]Wu CH.Explicit asymptotic solution for themaximum-energy-release-rate problem［J].Int J，Solids Structures，1979，15:561-566.

［10]Amestoy M，Leblond JB.On the criterion giving the direction of propagation of cracks in the Griffith theory［J].Comptes Rendus，301，1985（2）:969-972（in French）.

［11]Taylor D，Cornetti P，Pugno N.The fracturemechanics of finite crack extension［J].Engineering Fracture Mechanics，2005，72（7）:1021-1038.

［12]丁遂栋，孙利民.断裂力学［M].北京：机械工业出版社，1997：148-169.

［13]杨卫.宏微观断裂力学［M].北京：国防工业出版社，1995：65-70.

［14]杨大鹏，赵耀，白玲.准静载荷作用下的弹塑性微弯延伸裂纹塑性区［J].应用力学学报，2010，27（2）:401-405.

［15]杨大鹏，赵耀，白玲.准静载荷作用下的弹塑性微弯延伸裂纹张开位移［J].应用力学学报，2010，27（3）:574-578.

［16]胡志忠，曹淑珍.形变硬化指数与强度的关系［J].西安交通大学学报，1993，27（6）：71-76.

［17]汤卉，沙宇，张嘉振.不同加载条件压载荷对疲劳裂纹尖端塑性区的影响［J].机械工程师，2008（4）:88-89.

［18]陈篪.考虑到硬化的塑性区修正［J].力学学报，1975（2）:78-80.