一类利用Catas算子定义的p叶解析函数类
阚兴莉
(湖北工业大学商贸学院,湖北 武汉 430079)
0 引言
设A(p,n)表示在单位圆盘U={z∈C:|z|<1}内p叶解析且具有如下泰勒展开式
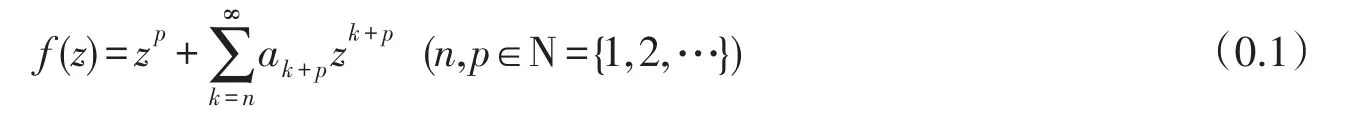
的函数族,并记A(1,1)=A,T(p,n)表示A(p,n)中由下式组成的函数集合:
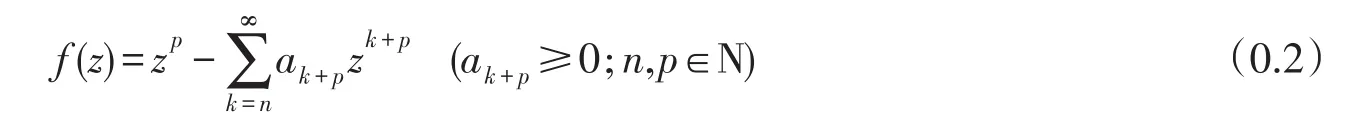
Darwish等[1]介绍了A(p,n)中的函数类β-UST(α,β,p,n):
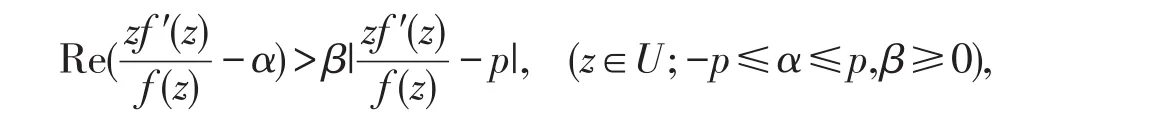
和β-UCV(α,β,p,n):
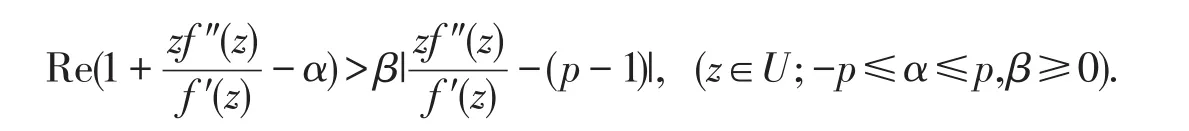
显然,f(z)∈β-UCV(α,β,p,n)当且仅当zf′(z)∈β-UST(α,β,p,n).对上述函数类中参数进行适当的赋值,可以得到以下函数类:
1)S(p,n,α)=β-UST(α,0,n,p),K(p,n,α)=β-UCV(α,0,p,n)由 Owa[2]引入并研究,S∗(p,α)=S(p,1,α),K∗(p,α)=K(p,1,α)分别称为α阶星象函数和α阶凸函数,由Patil和Thakare[3]引入并研究;
2)UST(α,β)=β-UST(α,β,1,1),UCV(α,β)=β-UCV(α,β,1,1)由 Bharathi等[4]引入并研究;UCV(0,β),UCV(0,1)分别由Goodman[5]和Kanas等[6]引入并研究.
对函数类A,Nishiwaki等[7]改变参数α和β的取值范围,引入了新的函数类MD(α,β):
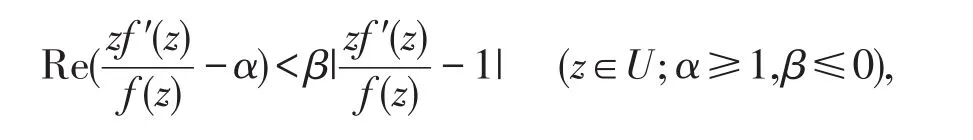
和ND(α,β):
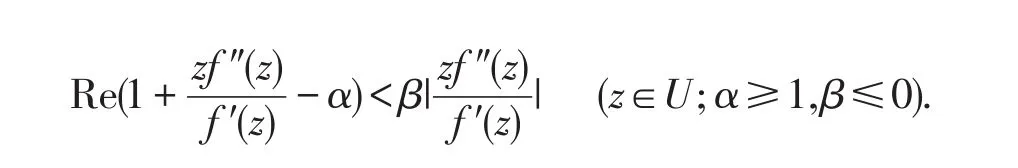
容易验证,f∈ND(α,β)当且仅当zf′∈MD(α,β).对于其他类型的函数类可参见文献[8-10].
设f∈A(p,n),η,λ,l≥0 ,Catas[11]定义了A(p,n)上的算子函数Ⅰp(η,λ,l)(称为Catas算子)为:
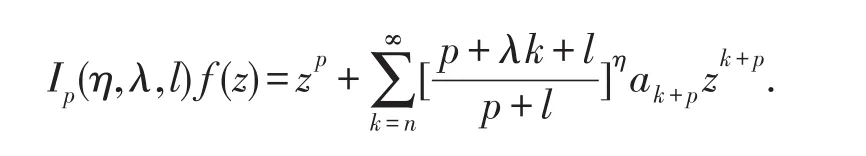
在Catas算子中对参数p,η,λ,l做适当的赋值,可以得到一些特殊形式的算子,具体参见文献[12-18].本文中利用Catas算子,定义一类新的函数类S(α,β,p,n,η,λ,l):
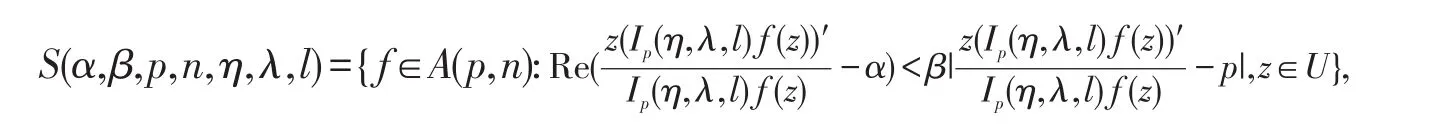
这 里α≥p,β≤0. 容 易 验 证 ,MD(α,β)=S(α,β,1,1,η,0,l). 为 下 面 叙 述 方 便 ,记S0(α,β,p,n)=S(α,β,p,n,η,λ,l),TS0(α,β,p,n)=S0(α,β,p,n)⋂T(p,n).笔者利用一些不等式的技巧研究函数类TS0(α,β,p,n)的系数不等式、星象半径、凸半径、极值点,推广了一些已有的结论.
1 系数不等式
定理1.1若由(0.1)式定义的函数f(z)∈A(p,n)满足下面不等式
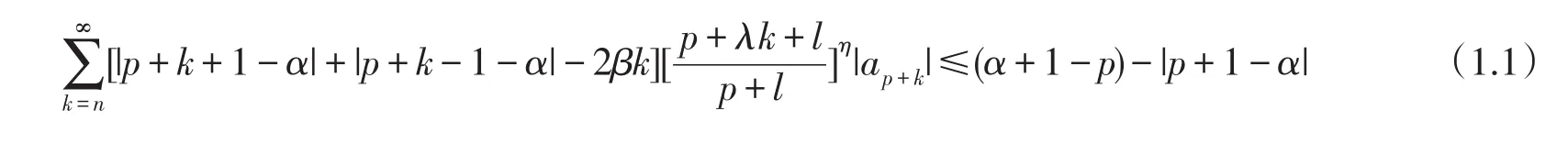
则f(z)∈S0(α,β,p,n).
定理1.1的证明为证明方便,假设
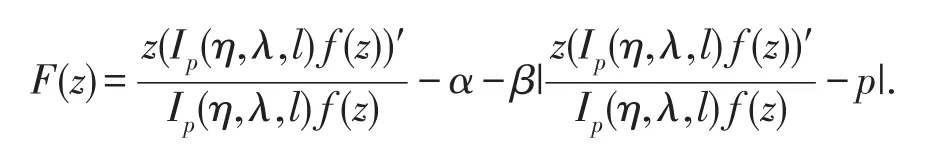
若则ReF(z)<0 ,即f(z)∈S0(α,β,p,n).又因为

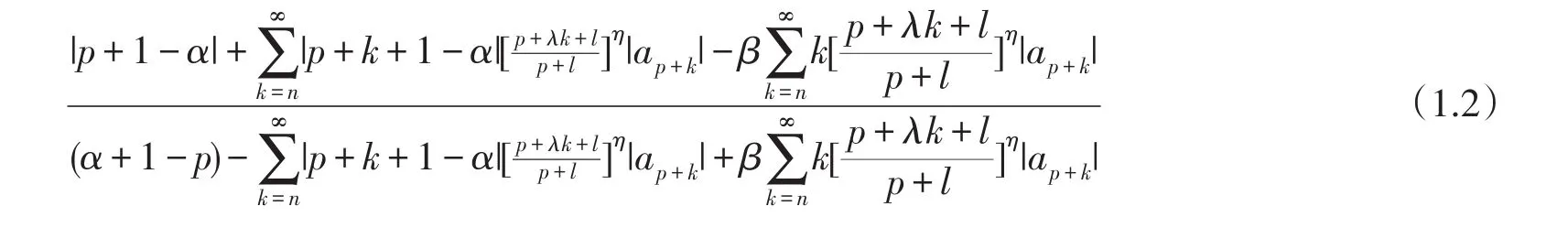
由于f(z)满足(1.1)式,将(1.1)式变形,得
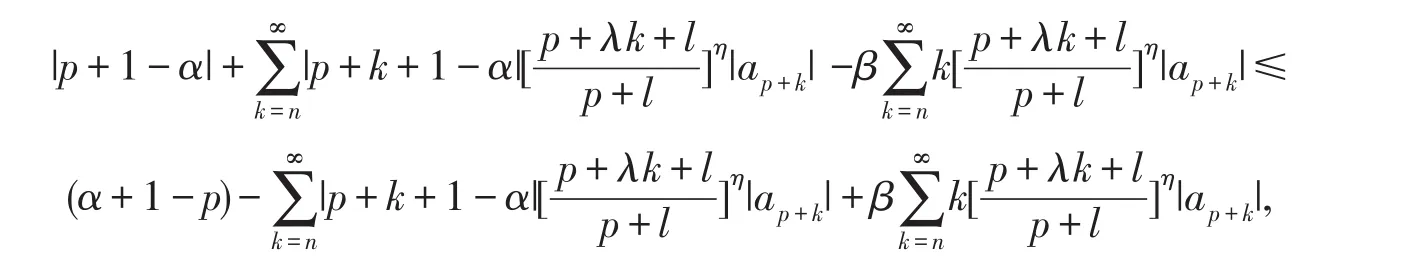
即(1.2)式的最后的一个表达式有上界1,所以f(z)∈S0(α,β,p,n),定理得证.
特别地,当p=1,n=1,λ=0时,有下面的推论成立.
推论1.2[7]若f(z)∈A,满足不等式
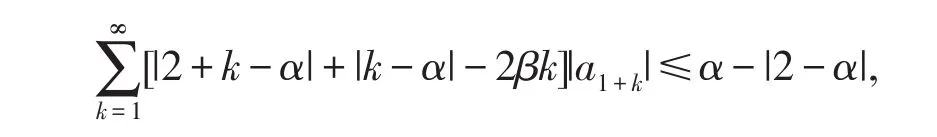
则f(z)∈MD(α,β).
推论1.3[7]若f(z)∈A,满足不等式
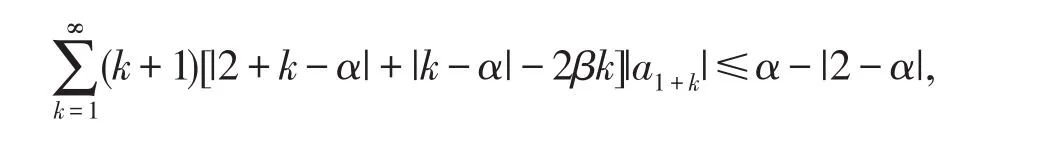
则f(z)∈ND(α,β).
推论1.4设f(z)∈TS0(α,β,p,n),则
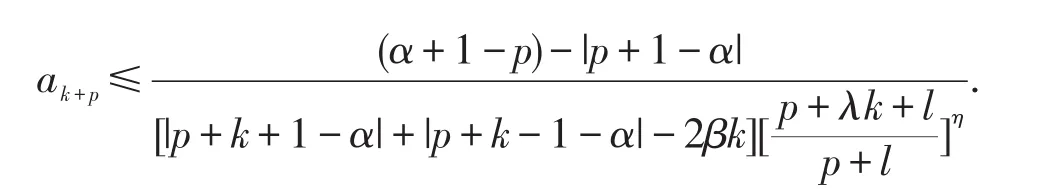
2 星象半径、凸半径
定理2.1设f(z)∈TS0(α,β,p,n),f(z)在|z|=r1上为δ(0≤δ<p)阶星象函数,这里
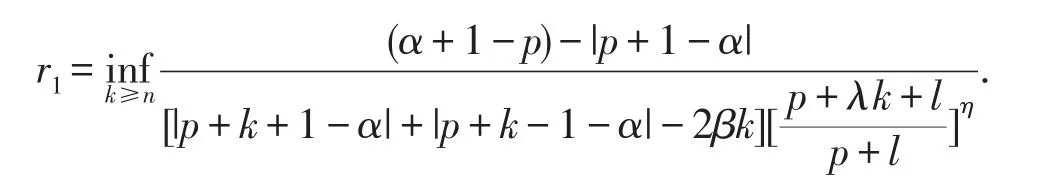
定理2.1的证明由星象函数的定义,为了得到结论,只需

而

因此,如果
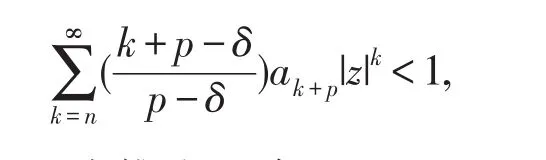
则(2.1)式成立.又由于f(z)∈TS0(α,β,p,n),由推论1.4知
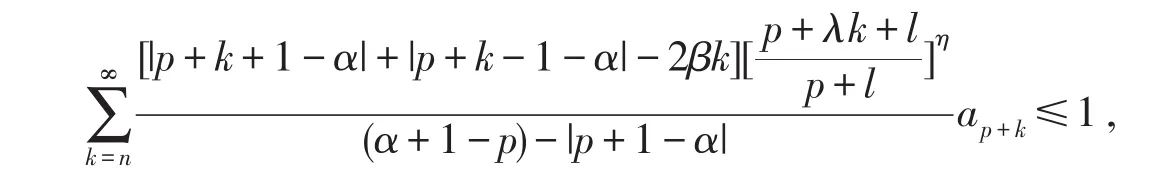
所以,只要不等式
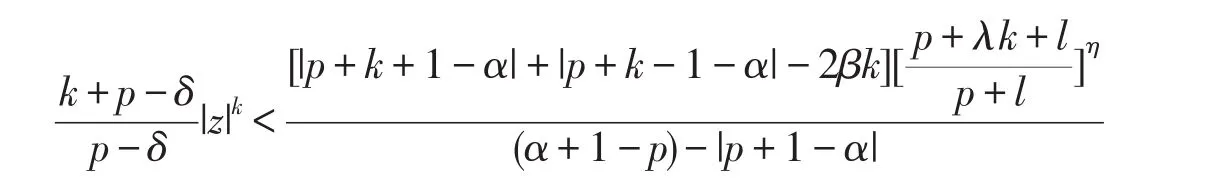
成立即可,上述不等式变形即为
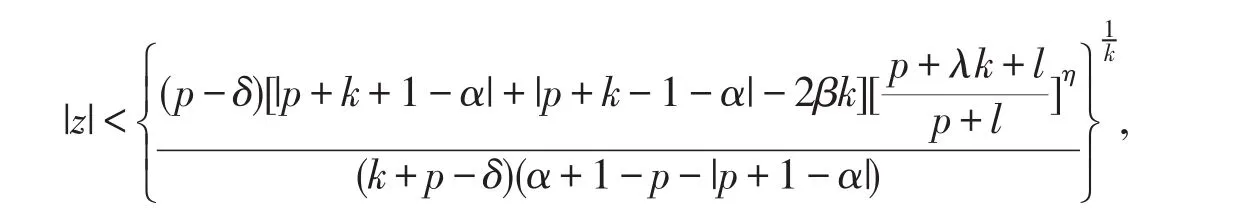
取
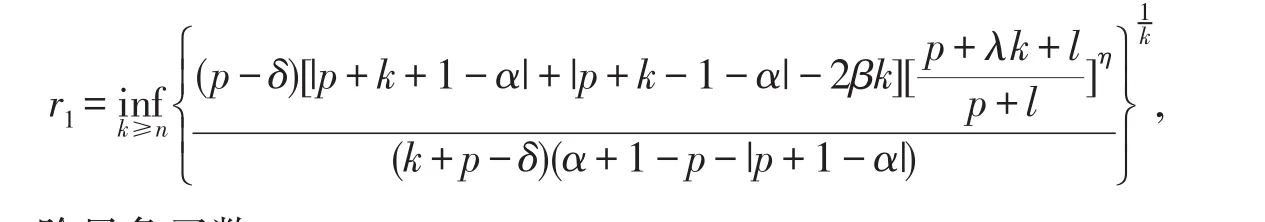
在|z|=r1上,f(z)为δ阶星象函数.
定理2.2 设f(z)∈TS0(α,β,p,n),f(z)在|z|=r2上为δ(0≤δ<p)阶凸函数,这里
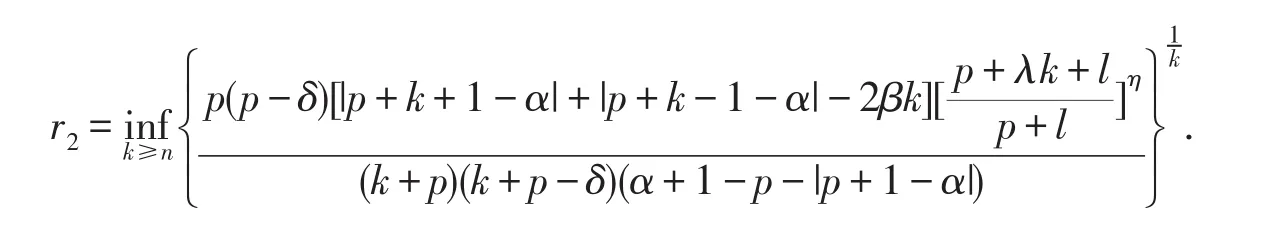
定理2.2的证明由凸函数的定义,为了得到结论,只需

而
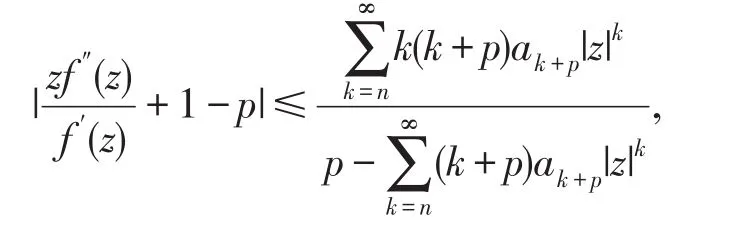
因此,如果
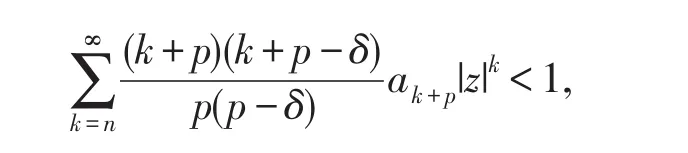
则(2.2)式成立.又由于f(z)∈TS0(α,β,p,n),由推论1.4,知
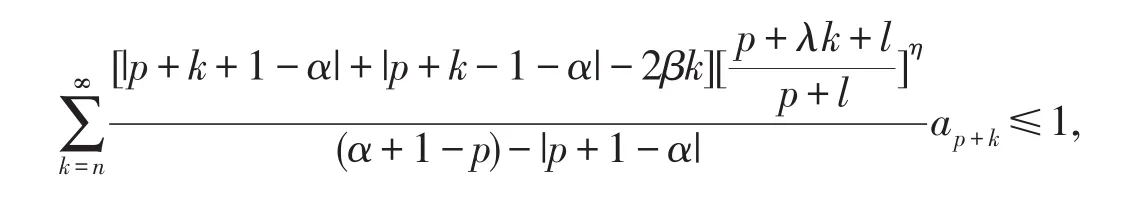
所以,只要不等式
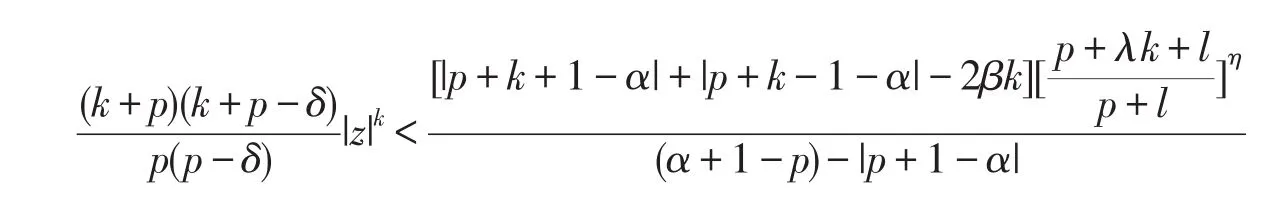
成立即可,上述不等式变形即为
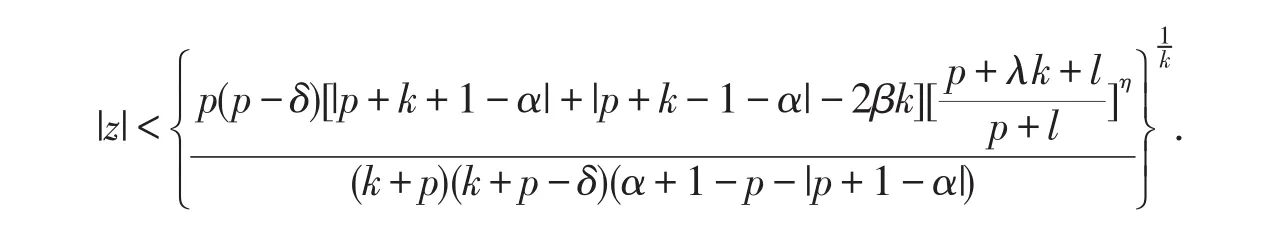
取
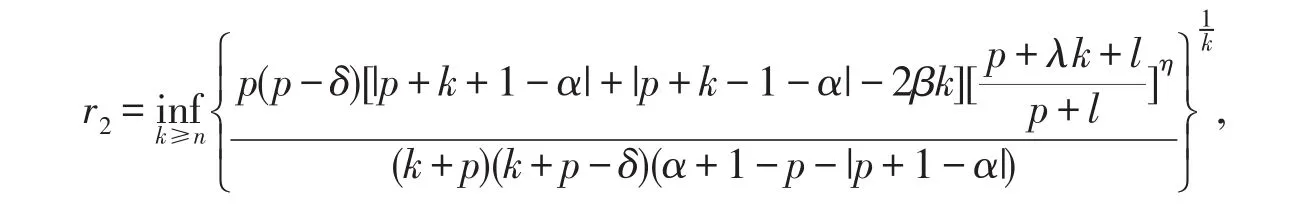
f(z)在|z|=r2上为δ(0≤δ<p)阶凸函数.
3 极值点
定理3.1设则f(z)∈当且仅当

这里
定理3.1的证明先证明充分性.假设
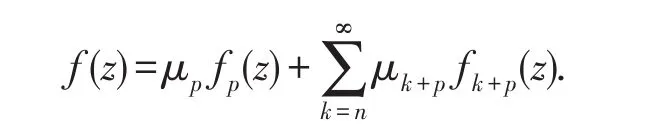
将fp(z),fk+p(z)代入f(z),得
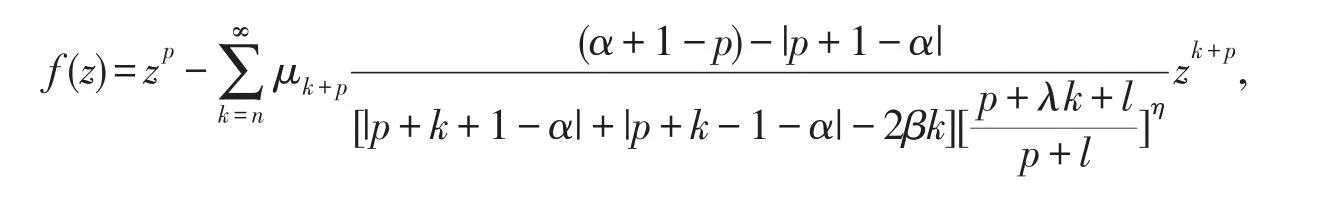
利用定理1.1知,
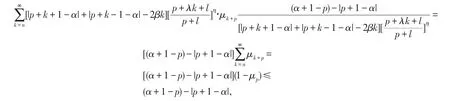
所以f(z)∈TS0(α,β,p,n).
再证明必要性.令f(z)∈TS0(α,β,p,n),因为
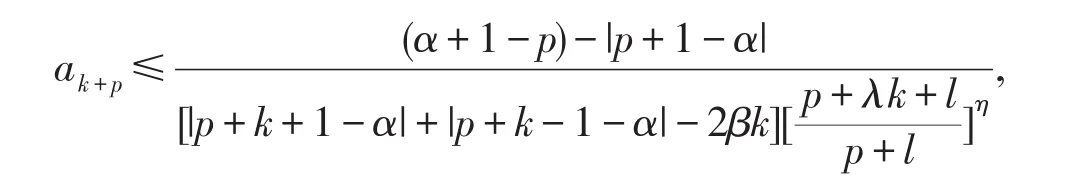
令
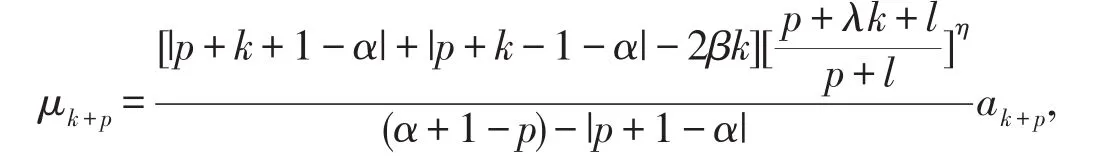
且
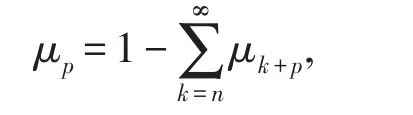
由于
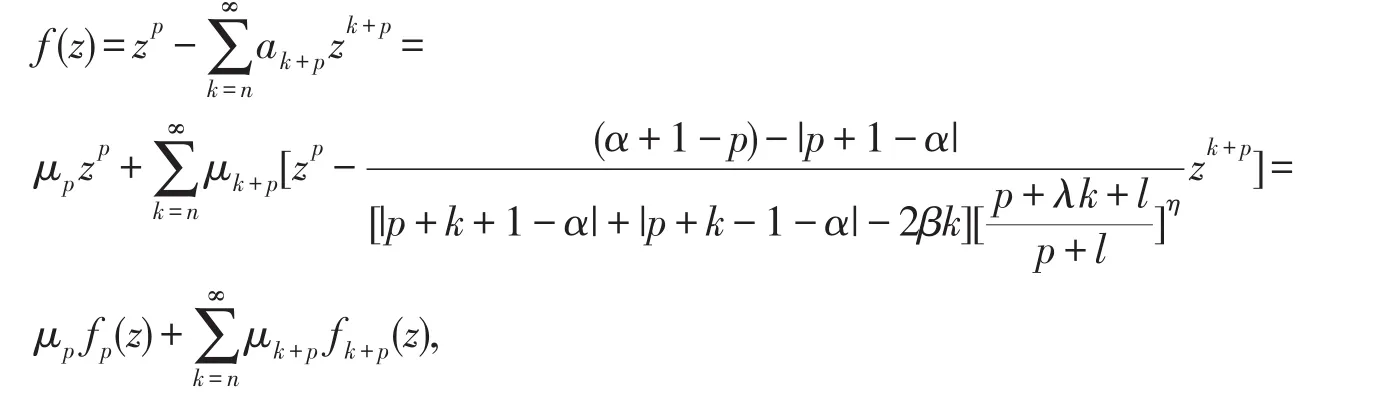
结论得证.
推论3.2TS0(α,β,p,n)的极值点由下列函数
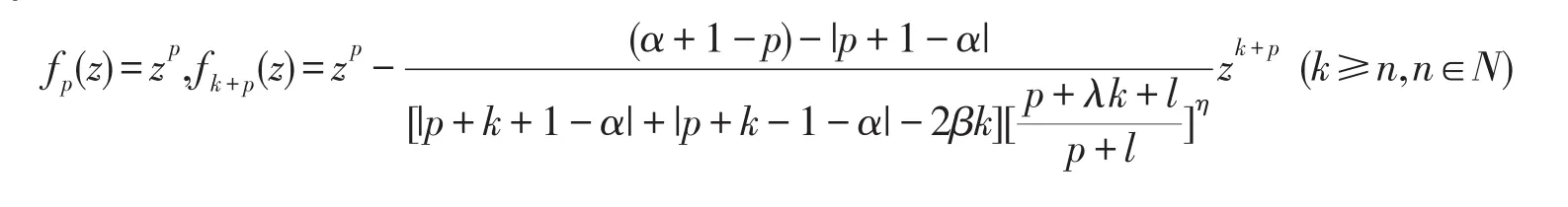
构成.
[1]Darwish H E,Magesh N.On certain subclasses of multivalent analytic functions involving the catas operator[J].Acta Universitatis Apulensis,2013,36:209-224.
[2]Owa S.Some properties of certainmultivalent functions[J].ApplMath Lett,1991,4(5):79-83.
[3]Patil D A,Thakare N K.On convex hulls and extreme points ofp-valent starlike and convex classeswith applications[J].BullMath Soc SciMath,1983,27(2):145-160.
[4]Bharati R,Parvatham R,Swaminathan A.On subclasses of uniformly convex functions and corresponding class of starlike functions[J].Tamkang JMath,1997,28(1):17-32.
[5]Goodman AW.On uniform ly convex functions[J].Ann Polon Math,1991,56(1):87-92.
[6]Kanas S,Wisniowska A.Conic regionsandk-uniform convexity[J].JComputApplMath,1999,105(1):327-336.
[7]Nishiwaki J,Owa S.Certain classes of analytic functions concerned with uniform ly starlike and convex functions[J].Appl Math Comput,2007,187:350-355.
[8]李小飞,熊良鹏.一类解析函数类的凸性[J].湖北大学学报:自然科学版,2014,36(2):166-169.
[9]赫小娜.解析函数族的近于凸性[J].湖北大学学报:自然科学版,2011,33(3):336-339.
[10]蔡振锋.一类近于凸函数子族的研究[J].湖北工业大学学报:自然科学版,2009,24(5):84-88.
[11]Catas A.On certain classes of p-valent functions defined bymultiplier transform presented paper[C].Proceedings of the International Symposium on Geometric Function Theory and Applications,Istanbul,Turkey,2007.
[12]Acu M,Owa S.Note on a class of starlike functions[C].Proceedings of the International Short JointWork on Study on Calculus Operators in Univalent Functions Theory,Kyoto,Japan,2006.
[13]Al-Oboudi FM.On univalent functionsdefined by a generalized Salagean operator[J].Int JMath Math Sci,2004,25:1429-1436.
[14]Catas A.Neighborhoods of a certain class of analytic functionswith negative coefficients[J].Banach JMath Anal,2009,3(1):111-121.
[15]Cho N E,Srivastava H M.Argument estimates of certain analytic functions defined by a class ofmultiplier transformations[J].Math ComputMode,2003,37:39-49.
[16]Cho N E,Kim TH.Multiplier transformations and strongly close-to-convex functions[J].Bull Korean Math Soc,2003,40(3):399-410.
[17]Kumar SS,Taneja H C,Ravichandran V.Classes ofmultivalent functions defined by Dziok-Srivastava linear operator and multiplier transformation[J].Kyungpook Math J,2006,46(1):97-109.
[18]Wang Z G,Xu N,Acu M.Certain subclasses ofmultivalent analytic functions defined bymultiplier transforms[J].Appl Math Comput,2010,216:192-204.

