不确定QoS信息下的web服务选择方法研究①

吴青林，周天宏

（1.郧阳师范高等专科学校计算机科学系，湖北 十堰 442000；2.武汉商学院信息工程系，湖北 武汉 430056）

0 引言

随着面向服务体系结构、云计算以及软件即服务等技术的发展，web服务发展成为面向服务体系结构软件的重要形式，已广泛应用到电子商务、教育、工业等多个领域.当前web服务数据迅速增长，用户对web服务的需求日益多样化，在服务的选择过程中不仅需要考虑web服务的功能属性，也需要考虑其非功能属性.在web服务环境中，当前国内外学者提出了一些基于QoS属性的web服务选择方法，大多数采用确定的QoS属性信息实现服务选择，而web服务处于开放的环境中，一些QoS指标受到网络环境变化、任务数等诸多外部因素的影响，以及服务用户应用上下文环境的复杂性和服务提供者资源调度的灵活性等特点，web服务的QoS值会发生变化，具有不确定性因素，以确定值的形式给出QoS属性无法准确描述web服务受开放环境的影响程度，不利于最优候选服务的选取［1-5].

如何在web服务选择过程中分析和量化不确定QoS信息已经成为web服务领域内迫切需要解决的关键问题，充分考虑不确定QoS信息对更加准确地实现web服务组合具有重要的意义.针对当前对web服务选择研究中对不确定QoS信息考虑不充分的问题，根据QoS属性描述内容和获取方式不同对QoS属性进行分类，并以此为基础提出一种不确定QoS信息下服务选择的方法.该方法采用有序加权平均（OWA）算子来实现区间数的确定化，使用联系数分析和量化web服务的模糊QoS属性，并通过实例验证该选择方法的有效性，进一步提高用户web服务选择的响应时间和用户满意度.

1 web服务的QoS属性描述

web服务QoS属性指标种类繁多，主要是描述完成业务目标的特征，根据其描述的内容和获取方式不同，可以将其分为基础性指标、运行性指标、历史性指标和专用属性指标，其分类结构图如图1所示［6-8]：

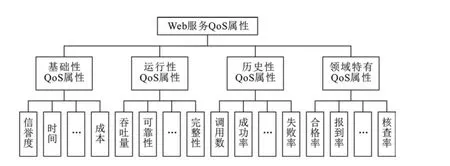
图1 web服务QoS属性结构图

1）基础性指标

基础性指标是指每个web服务都应该包括的通用指标，用户在进行服务选择时都需要考虑.主要包括成本、时间、信誉度等.基础性指标为web服务选择提供重要的判断依据.

2）运行性指标

运行性指标主要包括运行时的一些QoS属性，主要包括可见性、可访问性和完整性等服务运行性能的描述，在为web服务组合的服务选择中发挥重要的参考作用.

3）历史性指标

历史性指标主要是通过对web运行记录进行统计得到，如服务被调用次数、成功次数和失败次数等，这些由客户或目录服务统计的客观性服务质量，在服务选择中起到一定的参考作用.

4）领域特有指标

专用指标是指特定领域的服务所持有的服务质量指标.如产品类服务的“合格率”，天气类服务的“温度”等，web服务应当具有的领域特有指标一般通过领域本体来描述.

2 web服务QoS属性确定化

web服务的QoS属性的度量方法、量纲、表达方式等都不尽相同，具有多样化的特点.web服务QoS属性的多样性特征为web服务的选择增加了难度，需要对QoS属性进行确定化处理，以便更准确为抽象服务选择合适的web服务进行组合，该阶段对web服务组合具有重要作用.笔者根据QoS属性的描述方式，将不确定QoS属性分为区间型和模糊型，通过不同的处理方式分别将其确定化［9-12].

2.1 确定化思想决策思路是分别对区间型和语言型QoS属性提出解决方案，区间型QoS属性采用通过样本性质总体估计随机变化的QoS指标并通过有序加权平均（OWA）算子来实现QoS确定化，语言型QoS值数据模糊程度较高，通过转化成联系数的形式来刻画和分析web服务描述的确定与不确定联系.本文中提出的方法采用的联系数形式是:u=a+bi，其中a+b=1，a，b∈［0，1]，a表示同一度，b表示差异度，i为差异度系数，取值区是［-1，1]，当b=0时，联系数为一确定数，将联系数引入到web服务领域，能够很好地解决不确定QoS属性的web服务的选择问题.

2.2 区间型QoS属性处理

2.2.1 区间数的获取 当web服务的QoS属性值在一定的动态范围内随机变化时，采用样本的性质对随机变量总体性质进行估计，总体估计随机变化的QoS指标并通过有序加权平均（OWA）算子来实现QoS确定化，首先随机选取web服务的n次执行记录值，分别确定不同QoS指标值的样本向量，设web服务的其中一个QoS属性值的样本向量为：Qi={q1,q2,q3,…,qn}，通过（1）式和（2）式得到其样本值的数学期望

2.2.2 区间数的确定化 区间的确定化依据美国著名学者Yager提出的有序加权平均（OWA）算子来实现，其基本思想是对数据按顺序排列，通过数据所在位置进行加权再进行集结，以实现区间数不确定信息的融合，并将其转化成确定数.为了更好地描述区间数的确定化，将涉及到的基本区间单调函数COWA算子定义如下：

定义1设Q函数:［0，1]→［0，1]，性质为：①Q（0）=0；②Q（1）=1③如果x≥y，则Q（x）≥Q（y），则Q称为基本的区间单调函数.

定义2设xˉ=[xl,xu]为区间数，并且：

其中Q为基本区间函数，称fQ为连续区间间OWA算子，简称COWA算子.

本文中主要通过COWA算子实现区间QoS值的确定化，设Q（y）=yr（r≥0）时，COWA算子可以表示为（3）式:

当r取不同的值时对应不同的结果如（4）式：

2.3 模糊QoS属性确定化

2.3.1 将模糊型QoS值转换为三角模糊数 模糊型QoS属性通常分为语言型、等级型、是否型和决策型，设三角模糊数u=［aL，aM，aN]（0＜aL＜aM＜aN），则称u是一个三角模糊数，并且把aL、aN称为三角模糊数的下确界和上确界，称aM为三角模糊数的中值，称aN-aL为三角模糊数的取值区间.先将其转换为三角函数，其转换规则分别为：

1）语言型：如果ij是（0≤j≤m）为语言集i=＜i0，i1，i2，…，in＞的一个属性值，则转换成三角模糊数为（（j-1）/m，j/m，（j+1）/m）.

2）等级型：如果li（0≤i≤m）是有序等级集合L=＜L0，L1，…，Ln＞的一个属性值，则该属性的三角模糊数为＜li/lm，li/lm，li/lm＞.

3）是否型:是否型属性值包括“是”和“否”两种情况，如果值为“是”，则其三角模糊数可表示为＜1，1，1＞，如果其值为“否”则其三角模糊数表示为＜0，0，0＞.

4）决策型:如果n属性为决策模型的评价值，则0≤n≤1，则该决策值的三角模糊数为（n，n，n）.

2.3.2 数据采集及模糊数的确定化 选取n个用户的反馈值的中较大概率的评价值作为三角模糊数值，将三角函数值转化成确定数通过三元联系数的方法实现.

1）联系数的加法和乘法计算法则

①设u1=a1+b1i，u2=a2+b2i是两个联系数，则两个联系数之和u1+u2为u=a+bi，记作u=u1+u2=a1+a2+（b1+b2）i=a+bi.

② 设u1=a1+b1i，u2=a2+b2i是两个联系数，则两个联系数之积u1×u2是一个联系数u=a+bi，记作u=u1×u2=（a1+b1i）×（a2+b2i）=a1a2+（a1b2+a2b1+b1b2）i=a+bi.

2）将三角模糊数转化成u=a+bi型联系数的转换方法

设三角模糊数u=［aL，aM，aN]，转化后的联系数中的a=(aL+aM+aN)/3 ，b={[(aL-A)2+(aM-A)2+则三角模糊数转化后的联系数

3 基于联系数的web服务选择模型

在web服务选择决策模型中服务提供者将服务在UDDI注册中心注册，服务请求者提出服务请求，通过日志信息库和服务信息库获取相关信息，然后根据不同类型的QoS属性选取相应的处理方法，其web服务选择模型图如图2所示：

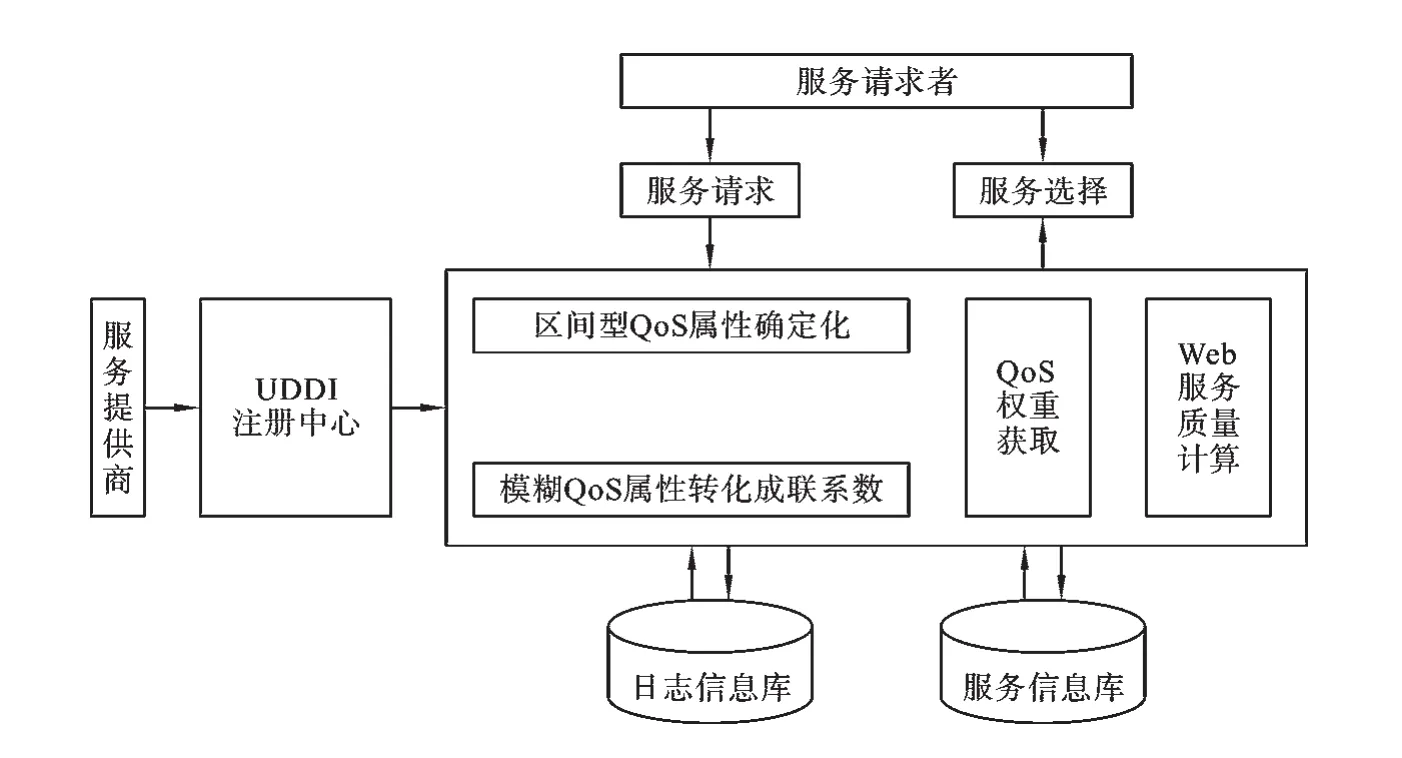
图2 web服务选择模型图

在该web服务选择模型中将web服务选择转化为一个多属性决策模型，具有相同功能的候选服务集合为获取的QoS属性并将其处理后的属性向量为q(si)={q1(si),q2(si),…,qm(si)}，其对应的属性权重为根据每个候选服务的QoS信息建立联系数决策矩阵，结合权重向量，即可计算出每个候选服务的服务质量，假设属性先经过规范化处理，属性值越大越好.则候选服务的质量计算分式为将上述公式模型利用三角模糊数表示即为：

其中i的取值范围为本文中根据比例取值原理取

4 实验

为了验证用户对本文中中推荐模型的有效性，在局域网中构建模拟环境，仿真实验的计算机配置是Pentium 3500MHz处理器，2G内存，win7操作系统，Matlab 8.1，模拟5个功能相同的服务，每个服务有4个质量属性，即响应时间（单位:ms），价格（单位:元），信任度和可用性.实验步骤如下：

1）分别调用候选服务30次，根据提出的方法计算区间型属性，选取较大概率数据作为模糊型属性，其质量属性区间和语言描述如表1所示：

表1 候选服务的服务质量的属性区间

2）根据表1的数据，用三角模糊数表示用语言描述的QoS值，语言描述集为：{很高，高，一般，较低，很低}，其属性矩阵如下：

3）根据本文中中提出确定化方法，将上述区间数和三角模糊数确定化，可得到确定化矩阵为:

4）先将上述数据进行标准化处理，并根据区间范围和三角模糊数转化成联系数的方法，对其进行标准化处理，建立联系数矩阵：

5）将三角模糊数转化成联系数的形式:

6）权重确定.QoS权重采用三角模糊数的形式表示，将其转化成联系数再参与计算，4个QoS属性的权重转换成联系数，其值分别为

7）综合QoS值.根据选择模型计算公式分别求出每个服务的质量联系数，结果分别为:

8）按照“i的比例取值原理”取值，计算综合值.

9）结果及分析.从以上综合值的排序，5个候选服务的质量排序为S3＞S5＞S4＞S1＞S2，本文中算法与多目标决策算法处理结果一致，并选择响应时间和用户满意度作为性能指标，将两种算法的性能进行对比.

①响应时间比较

本文中算法通过引入联系数，算法计算过程简单，其响应时间优于多目标决策算法，通过增加候选服务的数量个数，其响应时间保持平稳增加，没有发生明显的变化，两种算法的响应时间随服务数变化的比较如图3所示.

②用户满意比较

本文中提出的算法在候选服务数量小于30时，满意度与多目标决策算法大致相当，当候选服务数量大于30时准确性和用户满意度明显优于多目标决策算法，两种算法的满意度随候选服务数变化的比较如图4所示.

图3 响应时间对比

图4 用户满意度对比

5 小结

web服务QoS属性信息不确定性问题是web服务选择过程中迫切需要解决的关键问题，在已有研究成果的基础上，通过引入联系数的形式提出了web服务选择方法，实验证明该方法的可行性和有效性，在下一步的工作中，应该进一讨论如何将其应用于服务组合过程，提高服务组合的效率和准确性.

［1]温涛，李迎秋，盛国军，等.不确定信息下基于改进粒子群算法的web服务选择［J].吉林大学学报：工学版，2014，44

（1）:129-137.

［2]康国胜，刘建勋.考虑QoS属性相关性的web服务选择［J].小型微型计算机系统，2014，35（4）:786-789.

［3]祝希路，王柏.基于不确定服务质量的服务选择算法［J].计算机集成制造系统，2011，17（11）:2532-2539.

［4]王红兵，孙文龙，王华兰.Web服务选择中偏好不确定问题的研究［J].计算机学报，2013，36（2）:275-286.

［5]文俊浩，秦佳，柳玲.一种在用户偏好不确定情况下的web服务选择方法［J].计算机应用研究，2010，27（6）:2147-2149.

［6]赵克勤.二元联系数A+Bi的理论基础与基本算法及在人工智能中的应用［J].智能系统学报，2008，3（6）:477-488.

［7]董九英，万树平.三角模糊数型多属性决策的灰色关联法［J].计算机工程与应用，2010，46（15）:196-199.

［8]孙禄，卢潇，韩毅娜.基于三角模糊数的多目标群决策方法［J].化工自动化及仪表，2010，37（11）:73-77.

［9]张成文，苏森，陈俊亮.基于遗传算法的QoS感知的web服务选择［J].计算机学报，2006，29（7）:1029-1038.

［10]贺春林，谢琪.基于协同过滤的个性化web 服务选择方法［J].计算机应用，2013，33（1）：239-242.

［11]舒振，陈洪辉，罗雪山.基于改进混合粒子群算法的服务动态选择方法［J].中南大学学报:自然科学版，2011（10）:3086-3094.

［12]付晓东，邹平等.QoS信息不确定情况下的web服务选择［C].第二十七届中国控制会议论文集:271-276.