基于多极小值粒子群的自适应运动估计算法①

江波，张正文，刘凌云

（湖北工业大学电气与电子工程学院，湖北 武汉 430068）

0 引言

运动估计能够减少视频序列时间冗余，是各类视频编码算法广泛采用的一项重要技术.运动估计占据了总运算量的60%以上，其性能决定视频编码的质量和效率.块匹配算法是目前大多数视频编码标准采用的一种运动估计算法.全搜索（FS）算法精度最高，但其计算复杂度高，难以实现实时应用.为了提高编码效率，许多快速运动估计算法先后被提出，如三步法（TSS）、新三步法（NTSS）［1]、菱形法（DS）、自适应十字模式搜索法（ARPS）［2]等.上述算法都提高了运算速度，但都基于相同的假设：在整个搜索窗中搜索最佳匹配块时，误差函数只有一个最小值，随着距离最佳匹配点越近，匹配误差呈现单调递减状态.该假设易导致快速搜索算法陷入局部最优解，影响视频编码质量.一些复杂的运动情况下，匹配误差函数呈现多极小值状态，这种假设不成立.

为了解决运动估计的全局最优问题，遗传算法（GA）和粒子群算法（PSO）被应用到运动估计.虽然遗传算法能够解决全局最优问题［3-4]，却存在收敛速度慢、计算复杂度高等缺点.相比于遗传算法，粒子群算法收敛速度快、计算复杂度低、全局搜索能力更好［5].但标准粒子群算法［6]也是假设搜索区域只存在一个极小值，将其应用到块匹配运动估计［7]，存在陷入局部最优、易早熟、迭代后期收敛速度慢问题.

针对上述算法的缺点，提出一种基于多极小值粒子群优化算法（MMPSO）［8]的自适应块匹配运动估计方法，利用MMPSO能够搜索到目标函数的多个极小值点的特性，对不同运动程度的块采用不同的迭代次数，实现快速收敛找到所有极小值匹配块，极大提高搜索精度.

1 多极小值粒子群优化算法

为了实现多峰误差曲面下的全局最优，刘文远等［8]提出了多极小值粒子群优化算法（multimiminum particle swarm optimization，MMPSO）.MMPSO假设目标函数的解空间区域内包含一个或多个极小值，粒子群中粒子的飞行方向不再只受某一个最小值粒子的影响，而是受到离该粒子最近的极小值粒子所在位置的影响.粒子的速度和位置更新为：

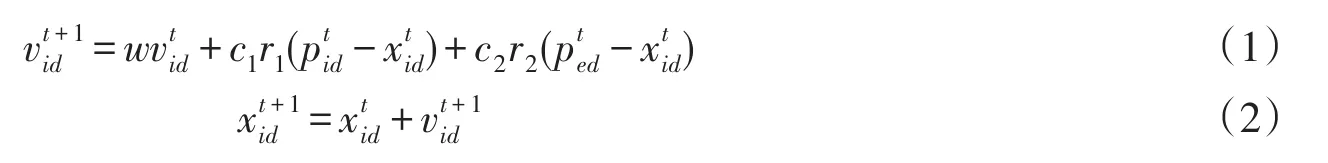
其中，w为惯性权值；d为搜索空间维数；t为粒子的迭代次数；vtid为粒子i第t次迭代时的速度；xtid为粒子i第t次迭代时的位置；c1、c2为学习因子；r1、r2为［0，1]之间均匀分布的随机数；ptid为粒子i寻找的最优解，即为个体极值；pted为离第i个粒子最近的极小值粒子第d维的位置坐标.

由于在MMPSO中粒子不受全局最优粒子位置的影响，而只受到距离该粒子最近的极小值粒子所在位置的影响，需要先找出上一代的极小值粒子，才能开始下一代的迭代.极小值粒子的具体寻找方法为:在离粒子i最近的的周围粒子中，将粒子i的适应值依次和周围粒子的适应值相比较，如果粒子i的适应值较大，则粒子i不是极小值粒子，继续选择其他粒子判断.如果第一个周围粒子的适应值较大，则继续判断粒子i周围的下一个粒子.如果粒子i的适应值小于等于粒子i周围每个粒子的适应值，那么粒子i就是一个极小值粒子.

2 基于MMPSO的自适应块匹配运动估计方法

2.1 粒子的定义和编码将块匹配方法中的宏块大小设为16*16，运动矢量的搜索范围为15*15.MMPSO算法中的粒子位置对应宏块运动矢量的水平和垂直分量Mv（xi，yi）.对搜索窗内点（x，y）相对于搜索窗中心的偏移进行编码.运动矢量的搜索窗范围和精度决定粒子的编码长度.编码方式采用Gray编码，由于Gray码相邻码字只有1位不同，在粒子迭代过程中容易移到相邻位置.单个坐标编码长度为［log2W+1]=5，总编码长度为L=10.因此，粒子Ci表示为：（xi，yi）T被编码成（xi，4，xi，3，xi，2，xi，1，xi，0，yi，4，yi，3，yi，2，yi，1，yi，0）T.其中W=max{sx，sy}；sx和sy分别为搜索窗的水平半径和垂直半径；xi，j=Gray（xi-x0）；yi，j=Gray（yiy0）；（x0，y0）T为搜索窗的中心位置坐标；xi，4和yi，4是运动偏移量的符号位.

2.2 定义适应度评价函数极小值粒子群优化算法采用适应度函数评价粒子的优劣，适应度大的粒子是最优值，而块匹配准则通常使用求和绝对误差SAD，误差值越小，块匹配精度越好.为使两者建立统一关系，采用当前匹配位置的Lagrangian代价函数［9]来计算适应度评价函数F（Ci）：

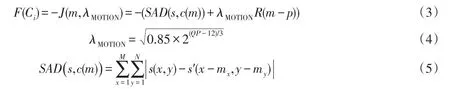
其中，SAD为M*N宏块的绝对误差和；m=（mx，my）T为运动矢量；p=（px，py）T为预测运动矢量；R（m-p）为编码运动矢量差所需码率；λMOTION为Lagrange算子；s表示原始宏块；s′表示运动矢量在参考帧中对应的预测宏块.通过（3）式计算每个粒子的适应度值，粒子对应位置的代价函数值越小，那么粒子适应度越高.

2.3 设定初代粒子在粒子群算法中，一般采用初代粒子随机产生的方法初始化种群.而在块匹配运动估计中，可以根据运动矢量特性选择初代粒子，从而提高搜索精确度和收敛速度.由于运动矢量具有以下特性：首先，运动矢量具有中心偏移特性，运动偏移大多数限制在搜索窗中心附近.其次，相邻的运动宏块具有相似性，可利用已经编码相邻宏块的运动矢量来预测当前宏块的运动矢量MVp，如图1所示，黑色块为当前等待匹配宏块.当前宏块的预测运动矢量为：MVp=（MV1+MV2+MV3）/3［10].

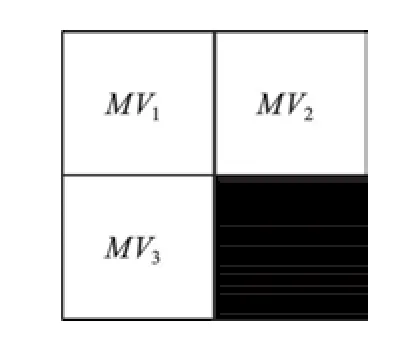
图1 运动矢量预测

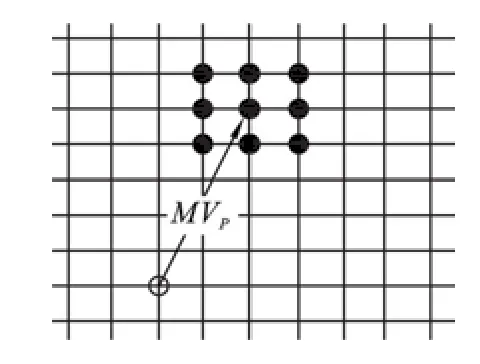
图2 初始种群位置分布

根据运动矢量以上两个特性选取MVp及其周围8个点作为初代粒子，如图2所示.

2.4 自适应运动强度视频序列中的运动强度各有差异，运动越剧烈，差异越大.对参考帧的运动幅度的标准差MⅠ进行量化处理，可以得到评估当前帧运动强烈程度的运动强度量化值MⅠ.

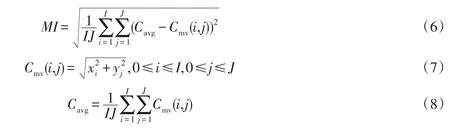
其中，Ⅰ和J为P帧中x和y方向上4*4块的个数；MⅠ为P帧运动幅度的标准差；Cmv（i，j）为P帧（i，j）块处的运动幅度；Cavg为P帧中4*4块的平均运动幅度；xi和yj为（i，j）块在x和y方向上的运动矢量.根据对标准视频序列中典型片段的分析［11]，运动强度量化值MⅠ小于40属于低运动强度；40到80之间属于中等运动强度；大于80属于高运动强度.对运动宏块进行自适应运动估计，减少搜索点数，提高运算效率.

2.5 迭代结束条件

1）粒子达到最大迭代次数Gmax时，粒子停止迭代，最终解为当代中最优解.为了研究迭代次数对搜索结果的影响，选取New、Coastguard和Football3个不同运动程度的序列代表，实验结果如图3所示.

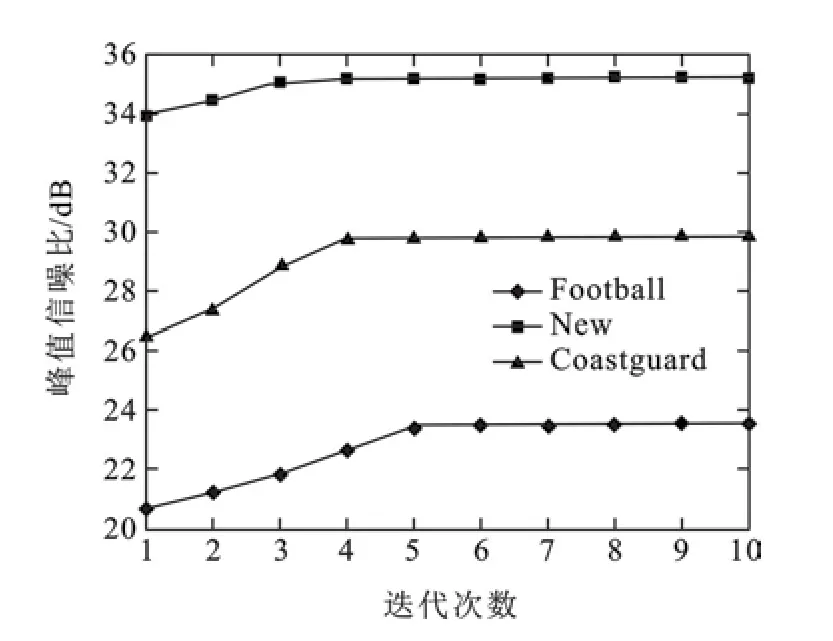
图3 不同运动强度的迭代次数与峰值信噪比

由图3实验可知，对于低运动强度的序列New、中等运动强度的序列Coastguard和高运动强度的序列Football，迭代次数Gmax分别达到3、4、5以后，PSNR值变化不大.迭代次数越大，搜索点数越多，因此可以根据图像运动复杂度确定Gmax，MⅠ＜40时，Gmax=3；40≤MⅠ≤80时，Gmax=4；MⅠ＞80时，Gmax=5.

2）粒子中含有满足运动估计块匹配条件的个体，个体粒子相应匹配位置的SAD值小于阀值ε，粒子停止迭代.不同运动强度的阀值也不同，MⅠ＜40时，ε=512；40≤MⅠ≤80时，ε=768；MⅠ＞80时，ε=1 024.

2.6 算法流程

1）计算当前宏块的预测运动矢量MVp，选取MVp及其周围的8个点作为初代粒子.

2）根据参考帧计算当前块的运动强度量化值MⅠ，确定粒子最大迭代次数Gmax.

3）计算粒子Ci的适应度F（Ci），判断当前位置的SAD值是否满足匹配条件.若满足SAD＜ε，转步骤8）；否则转步骤4）.

4）根据当前粒子的位置和适应值寻找当代粒子中的极小值粒子位置Ped.

5）根据极小值粒子的位置判断距离当前更新粒子最近的极小值粒子，并根据（1）式和（2）式更新这个粒子的速度和位置.

6）若达到最大迭代次数Gmax，转步骤8），否则转步骤7）.

7）根据（1）式和（2）式更新每个粒子的速度和位置，转步骤3）.

8）结束迭代，输出所有极小值粒子的大小及位置.

9）比较所有极小值粒点，最小的那个极小值点所对应的宏块即为最佳匹配宏块.

3 实验结果及分析

为验证算法的性能，选取了5种具有代表性的快速搜索算法FS、TSS、DS、GA和PSO进行实验.选取的宏块大小为16*16，搜索范围为15*15，当前帧与参考帧的帧间隔取为2帧.实验选取了5个图像序列的前100帧：低空间细节且运动缓慢的序列New（CIF，352*288，100帧）、中等空间细节且运动缓慢的序列Salesman（QCIF，176*144，100帧）和Coastguard（CIF，352*288，100帧）、高等细节且运动剧烈的序列Football和Tennis（SIF，352*240，100帧）.实验结果如图4、表1、表2所示.

图4显示的是Football视频序列每一帧中各算法与FS算法的PSNR差值.由图可以看出，TSS等算法与FS算法的PSNR差值变化较大，视频中运动变化大的部分陷入局部最优.而MMPSO算法具有较好的全局搜索特性，有效避免了局部最优，视频质量波动较小.

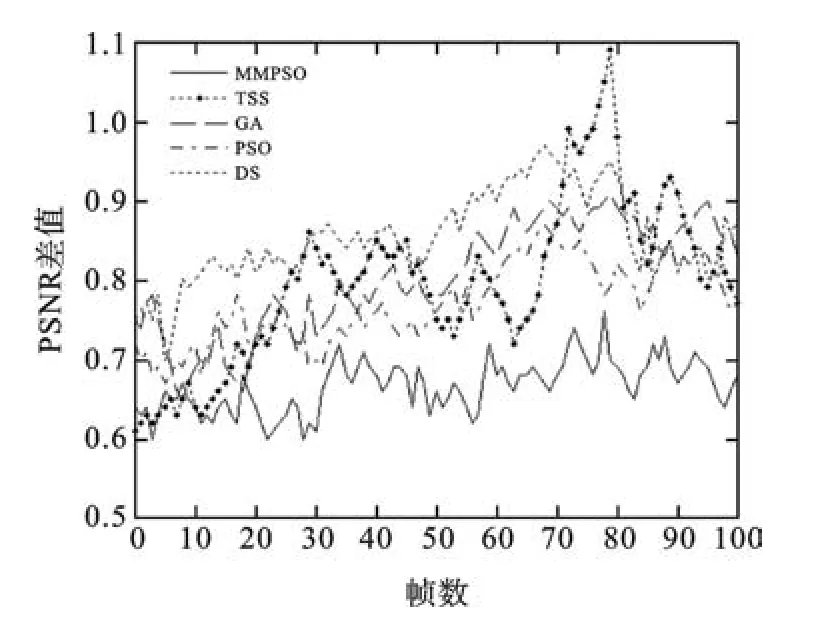
图4 各算法与FS算法的PSNR差值

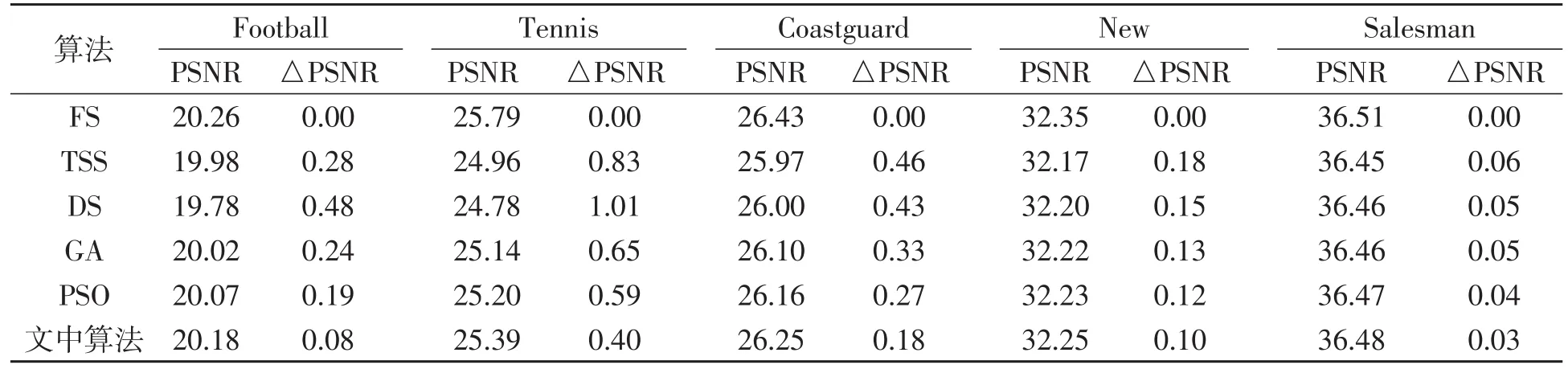
表1 6种算法平均PSNR值比较 dB

由表1可以看出，对于运动平缓的序列，这5种算法与FS算法的PSNR差值很小，因为大部分运动矢量分布在原点周围，单峰误差曲面假设成立.而对于运动中等和运动剧烈的序列，TSS、DS与FS的差值明显变大，因为大部分运动矢量远离原点，匹配误差呈现多峰值状态，单峰值误差曲面假设不成立，导致算法陷入局部最优.而GA和PSO具有全局搜索特性，PSO略优于GA，搜索精度都优于TSS和DS.

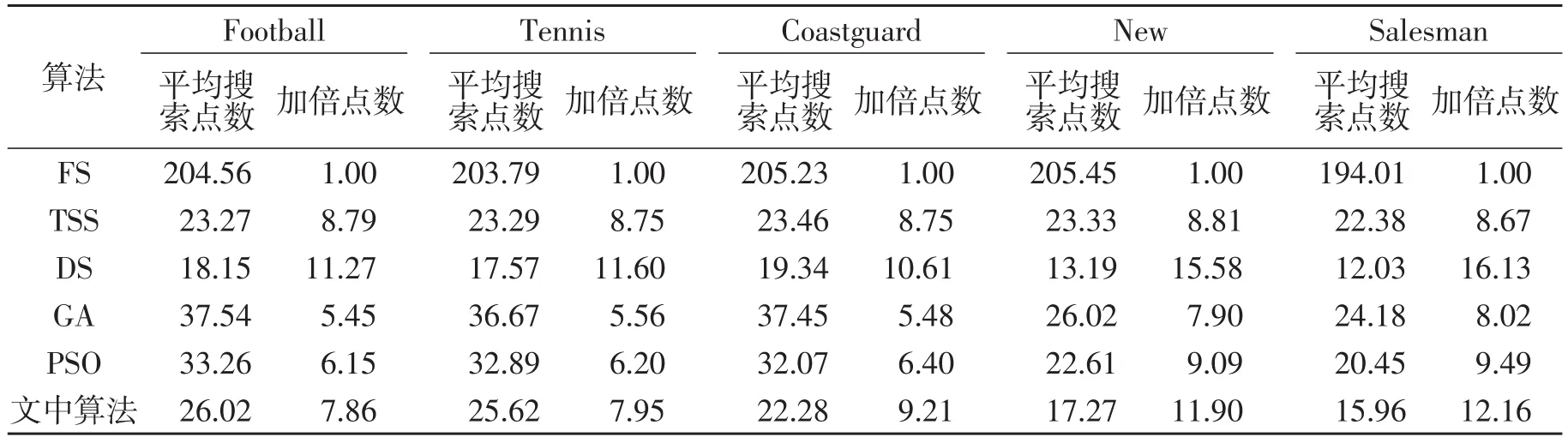
表2 6种算法平均每块搜索点数比较 次/像素

由表2可以看出，对于不同运动程度的序列，DS的搜索点数最少，TSS和DS算法的搜索点数波动不大，但算法的搜索精度低.GA算法的计算复杂高，导致各类视频序列的搜索点数增加，均高于TSS和DS.PSO算法的搜索点数比GA略有降低，但对于运动剧烈的视频序列，如Football和Tennis，其搜索点数还是很大，接近DS搜索点数的2倍.

综合考虑算法的搜索性能和计算复杂度，可以看出，对于运动平缓的New序列，以及运动中等的Salesman和Coastguard序列，MMPSO算法的搜索点数接近DS.而对于运动剧烈的Football和Tennis系列，MMPSO算法的搜索点数略有增加，接近TSS.对于各类运动强度的视频序列，在牺牲少量搜索速度的情况下，搜索精度大幅度提高，接近FS.

将多极小值粒子群优化算法应用到块匹配运动估计中，充分利用了其全局搜索、收敛速度快以及算法复杂度低的特点，并对不同运动程度的宏块采取自适应处理，避免了以往快速搜索算法容易陷入局部最优和早熟收敛的缺点.实验表明对于各类视频序列，MMPSO算法不仅保持了与TSS、DS相当的搜索速度，而且搜索精度明显提高，接近FS.但从实验数据分析可知，该算法的搜索速度有待提高.总之，MMPSO算法的整体性能优于以往快速搜索算法，适应不同运动情况下的视频编码需求.

［1]LIRenxiang，ZENG Bing，LIU Ming.A new three-step search algorithm for block motion estimation［J].IEEE Trans on Circuitsand System for Video Technology，1994，4（4）:438-442.

［2]SHENOLIKARPC，NAROTESP.Differentapproaches formotion estimation［C]//IEEEConference on Control，Automation，Communication and Energy Conservation，Tamilnadu，India，2009.

［3]CHOW K H K，LIOU M L.Genetic motion search algorithm for video compression［J].IEEE Trans Circuits Syst Video Technol，1993，3（6）:440-445.

［4]XU T B，CHENW D.A fast adaptive statistical genetic motion search algorithm for H.264/AVC［C]//IEEE Conference on Advanced Information Networkingand Application，Vienna，Austria，2006:553-558.

［5]EBERHARTR C，SHIY.Comparison between genetic algorithms and particle swarm optimization［C]//Proc IEEE Int Conf Evol Comput，Anchorage，AK，1998:611-616.

［6]KENNEDY J，EBERHARTR.Particle swarm optimization［C].IEEE International Conference on Neural Networks，Perth，Australia，1995:1942-1948.

［7]NIYAZI SORKUNLU，UGUR SAHIN，FERAT SAHIN.Block matching with particle swarm optimization for motion estimation［J].IEEE International Conferenceon Systems，Man，and Cybernetics，2013，13（16）:1306-1311.

［8]刘文远，郭香军.多极小值粒子群优化算法［J].小型微型计算机系统，2013，34（2）:351-355.

［9]LIZ，TOURAPISAM.Motion estimation with entropy coding considerations in H.264/AVC［C]//IEEEConference on Image Processing，San Diego，CA，2008:2140-2143.

［10]CHUN-HO CHEUNG and LAI-MAN PO.A novel cross-diamond search algorithm for fast block motion estimation［J].IEEE Transactionson Circuits and Systems for Video Technology，2002，12（12）:1168-1177.

［11]郭晓珉，姚睿，刘智跃，等.利用运动强度判据的高效自适应运动估计算法［J].中国图象图形学报，2012，17（4）:504-511.

［12]候志荣，吕振肃.基于MATLAB的粒子群优化算法及其应用［J].计算机仿真，2003，20（10）:68-70.