广义分式规划的对偶性

李向有，张庆祥

（延安大学数学与计算机学院 陕西 延安 716000）

0 引言

B-(p,r)不变凸函数[1]是一类重要的不变凸函数，很多学者利用这一函数研究了大量凸规划，得到了许多重要结论[2-6].但是这些文章只是利用B-(p,r)不变凸函数研究了常规的单目标规划问题，并且研究内容有很大的重合，Anurag Jayswal[7]研究了极大极小分式规划问题，对文献[8-9]中的相关结论进行了推广.上述文献都是利用B-(p,r)不变凸函数，研究相应的规划问题，没有对B-(p,r)不变凸函数进行推广.极大极小分式规划是凸规划里的一个重要研究内容，如文献[8-11]中利用不同的凸函数研究了相应极大极小分式规划问题最优性和对偶性问题.在上述文章的基础上，定义了一类新的广义凸函数：B-(p,r,a)不变凸函数、B-(p,r,a)不变拟凸函数、B-(p,r,a)不变伪凸函数，这些函数是对B-(p,r)不变凸函数的重要推广，并用这些函数研究了极大极小分式规划问题，在更弱的凸性下，对文献[8-11]中的相关结论进行了更大的推广，得到了一些重要结果.

1 基本定义

实值函数f:Rn→R是局部Lipschitz的，若对任意x∈Rn，存在一个正数k和x的邻域N()x，对任意y,z∈N(x)，使得‖f(y)-f(z)‖ ≤k‖y-z‖.

若函数f为局部Lipschitz的，那么函数f:X→R在x沿方向d的Clarke广义方向导数和Clarke广义方向梯度分别定义为：

定义1设非空开集X⊂Rn,f:X→R是X上的Lipschitz函数，p,r是任意非零实数，u∈X,若∀x∈X，存在向量函数η:X×X→Rn，函数b:X×X→R+，a:X×X→R，使得对∀ξ∈∂f(u)有：

成立，则称f在u点为关于函数η的B-(p,r,a)不变凸函数.

定义2设非空开集X⊂Rn,f:X→R是X上的Lipschitz函数，p,r是任意非零实数，u∈X,若∀x∈X，存在向量函数η:X×X→Rn，函数b:X×X→R+，a:X×X→R，使得对∀ξ∈∂f(u)有：

成立，则称f在u点为关于函数η的B-(p,r,a)不变拟凸函数.

定义3设非空开集X⊂Rn,f:X→R是X上的Lipschitz函数，p,r是任意非零实数，u∈X,若∀x∈X，存在向量函数η:X×X→Rn，函数b:X×X→R+，a:X×X→R，使得对∀ξ∈∂f(u)有：

成立，则称f在u点为关于函数η的B-(p,r,a)不变伪凸函数.

2 对偶性

考虑如下的分式规划问题：

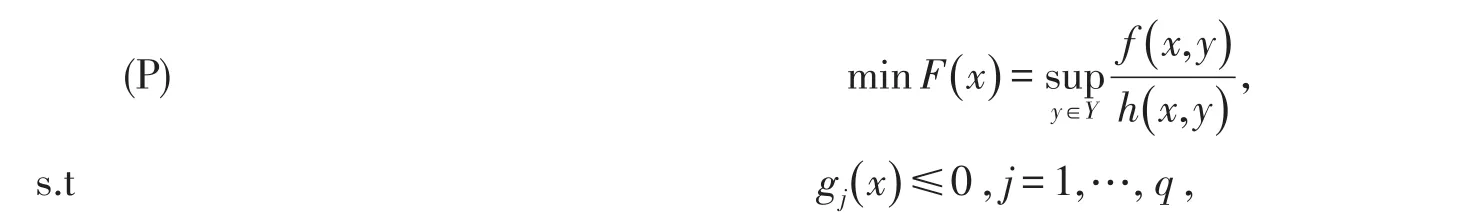
其中:x∈D⊆Rn，Y是Rm中的紧子集，f(.,.):Rn×Rm→R是Lipschitz函数且f(x,y) ≥0，h(.,.):Rn×Rm→R是Lipschitz函数，h(x,y) ＞0，g(.):Rn→Rp是 Lipschitz函数.J={1,2,…,q}，

K=现提出如下Mond-Weir对偶问题

这里H(s,λ,μ,y)表示满足条件(1)～(3)的 (z,λ,μ,y)的集合，如果H(s,λ,μ,y)是空集，则规定它的上确界为-∞.

定理1（弱对偶定理）假设

1)x,(z,s,λ,μ,yˉ)分别是（P），(FD)的可行解；

3)b0(x,z)＞0,b1(x,z)＞0 且a(x,z)+c(x,z)≥0,则

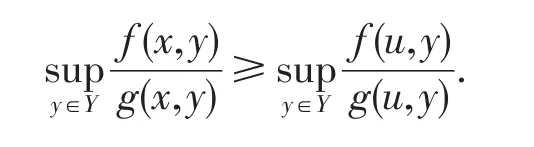
定理 1 的证明因为x,(z,s,λ,μ,yˉ)分别是（P），(FD)的可行解，所以有又b1(

x,z)＞0故有

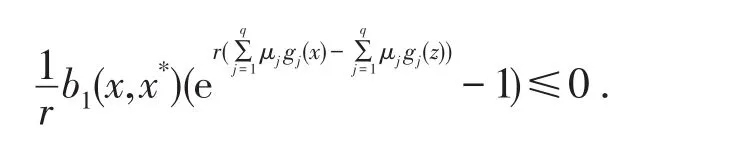
定理2（强对偶定理）假设

1)x0是（P）的最优解，∂gj(x0),j∈J(x0)线性无关，(z,s,λ,μ,yˉ)是(FD)的最优解；

2)ϕ(x)=在z处为关于函数η,b0的B-( )p,r,a不变伪凸函数，在z处为关于函数η,b1的B-( )p,r,a不变凸函数；

3)b0(x,z)＞0,b1(x,z)＞0且a(x,z)+c(x,z)≥0.则（P）和(FD)的最优值相等.

证明类似于文献[6]中定理3的证明.

定理3（严格逆对偶定理）假设

1)x0是（P）的最优解，∂gj(x0),j∈J(x0)线性无关，(z,s,λ,μ,yˉ)是(FD)的最优解；

2)ϕ(x)=在z处为关于函数η,b0的B-( )p,r,a不变凸函数，在z处为关于函数η,b1的B-(p,r,a)不变拟凸函数；

3)b0(x,z)＞0,b1(x,z)＞0且a(x,z)+c(x,z)＞0.

则x0=z，即z也是（P）的最优解.

定理3的证明假设由于x0≠z,则由定理2可得（P）和(FD)的最优值相等.

又在z处为关于函数η，b1的B-( )p,r,a不变拟凸函数，故∃τj∈∂gj(z),使得

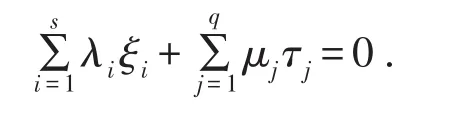
由（5-6）式和a(x,z)+c(x,z)≥0，可得

又ϕ(x)=在z处为关于函数η，b0的B-( )p,r,a不变凸函数，故

即有

于是存在i0，使得故有

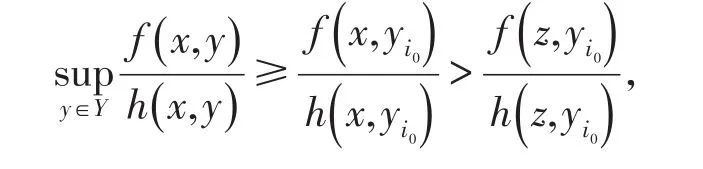
而这与定理2结论矛盾.

[1]Antczak T.A class of B -(p,r) invex functions and mathematical programming[J].J Math Anal Appl，2003，286:187-206.

[2]Liang Zhian，Zhang Zhenhua.The efficiency conditions and duality for uniform invex multiobjective program[J].OR Transactions，2009，13(1): 44-50.

[3]Zhang Ying，Zhu bo，Xu yingtao.A class of Lipschitz B -(p,r) -invex functions and nonsmooth programming[J].OR Transactions，2009，13(1): 61-71.

[4]Antczak T.Generalized B -(p,r) -invexity functions and nonlinear mathematical programming[J].Numerical functional Analysisand Optimazation，2009，30:1-22.

[5]孙玉华，张艳.B-(p,r)不变凸规划问题的最优性讨论[J].辽宁师范大学学报，2005，28(2):139-142.

[6]李向有，张庆祥.广义Ⅰ型函数的对偶性条件[J].贵州大学学报，2014，31(2):22-24.

[7]Anurag Jayswal.Non-differentiable minimax fractional programming with generalized α - univexity[J].Journal of computationaland applized mathematic，2008，214:121-135.

[8]Liu J C ，Wu C S . On minimax fractional optimality conditions with Invex[J]. J Math Anal Appl，1998，219:21-35.

[9]Liu JC ，Wu CS ，Shen R L.Duality for fractional minimax programming[J].Optimization，1997，41:117-133.

[10]Kim D S，Kim SJ.Optimality and duality for a class of nondifferentiable multiobjective fractional programming problem[J].J Math Anal Appl，2006，305:227-229.

[11]Soghra Nobakhtian.Optimality and duality for nonsmooth multiobjective fractional programming with mixed constraints[J].J Glob Optim，2008，41:103-115.