动车组旋修周期验证研究*

丁阳喜，唐玉杰，朱韶光，董孝卿，张现锋，王先亮

（1 华东交通大学，江西南昌330013；2 北京纵横机电技术开发公司，北京100081；3 中国铁道研究科学院 机车车辆研究所，北京100081；4 青岛四方庞巴迪铁路运输设备有限公司，山东青岛266111）

动车组旋修周期验证研究*

丁阳喜1，唐玉杰1，朱韶光2，董孝卿3，张现锋4，王先亮1

（1 华东交通大学，江西南昌330013；2 北京纵横机电技术开发公司，北京100081；3 中国铁道研究科学院 机车车辆研究所，北京100081；4 青岛四方庞巴迪铁路运输设备有限公司，山东青岛266111）

为验证某型动车组30万km旋修周期的合理性，对一个旋修周期内的动车组实测车轮进行磨耗分析，并将实测车轮外形输入到已建立的动力学模型中，计算动车组系统临界速度、构架横向稳定性、车体平稳性、曲线通能力等动力学性能，并参照相关标准进行评价。结果表明：车轮磨耗、等效锥度随运行里程增加变化平缓；运行31万km后车轮踏面与钢轨接触状态良好；所计算动力学性能均满足标准要求。从而验证某型动车组30万km里旋修周期的合理性。

旋修周期；动车组；30万km

动车组车轮磨耗会影响轮轨接触关系，显著影响运行的安全性、平稳性、舒适度，文献［1-3］均研究了实测磨耗踏面对动车组动力学性能的影响。为了改善轮轨接触关系，确保动车组安全、舒适地运营，铁路部门采用车轮旋修的方法进行维护，即对已偏离标准设计的车轮外廓进行旋修，以期恢复车轮与钢轨良好的接触状态。科学合理的旋修是保证动车组安全、舒适、经济运行的前提，国内外很多学者［4-6］都对此进行了研究。因我国动车组车型各异、线路众多，各运营动车组的磨耗状态也不尽同，文献［4］在长期对我国高速动车组的振动性能与磨耗状态进行大量跟踪测试的基础上，提出了旋修策略，即包括旋修周期制定与车轮踏面外形设计。旋修周期与动车组运行的安全性、平稳性、经济性密切相关，若车轮旋修周期过长，会导致车轮与钢轨接触状态恶化，降低乘坐舒适性，甚至会危及行车安全；若旋修周期过短，车轮踏面旋修频繁，旋修工作量大，车轮使用寿命短，经济性差。目前国内学者正在对既有运营线路上的动车组进行大量磨耗跟踪试验，优化旋修周期。

某型动车组在运营中出现了较为严重的车体晃动情况，旋修周期也无法达到30万km。在修改了车轮外形与优化减振器参数后，车体晃动情况消失，需要进一步确定车轮旋修周期以确保动车组安全、舒适、经济地运行。为此，对该型不同车号的多列动车组进行了多次磨耗跟踪试验［7］，文章以其中的某动车组M c2车为对象，就试验过程中采集的磨耗数据进行分析，再将实测车轮外形输入到已建立的动力学模型中，考察动车组的临界速度、轮重减载率、脱轨系数、轮轴横向力等，并与相关标准对比，从而验证动车组30万km旋修周期的合理性。

1　车轮磨耗分析

长期跟踪的某动车组自旋修后，已安全运营31.3万km。在此期间，进行了长达8次的磨耗跟踪试验，对整列动车组所有车轮进行测量，文中选取Mc2车的全部车轮外形，从踏面与轮缘随运行里程的变化规律、等效锥度随运行里程的变化规律两个角度来说明旋修周期内的车轮磨耗情况，从而验证动车组30万km旋修周期的合理性。

Mc2车一位轮对左轮和右轮旋修后实测踏面外形与运行31万km里后实测踏面外形对比如图1所示，红色轮廓线表示旋修后踏面，黑色轮廓线表示运行31k m里后踏面。图1显示：动车组运行31万km后滚动圆附近（70±20）mm处有明显的凹型磨耗，轮缘也有磨耗，Mc2车其他位轮对车轮均有此情况［7］。

该车所有车轮踏面与轮缘的磨耗量平均值随运行里程的变化规律如图2（a）。该车运行31万km之后，车轮踏面累计磨耗量平均值为1.22 mm，轮缘累计磨耗量平均值为1.00 mm；踏面和轮缘每10万km的平均磨耗分别为0.39 mm和0.32 mm。踏面与轮缘磨耗量在6万km之前快速增加，此后随运行里程增加缓慢增加，且两者趋势近似。在12万km之前轮缘磨耗速率高于车轮踏面磨耗速率，12万km以后，踏面磨耗速率高于轮缘磨耗速率。由上述分析可知：在此期间车轮踏面与轮缘磨耗随运行里程增加变化平缓，没有出现剧烈磨耗现象。

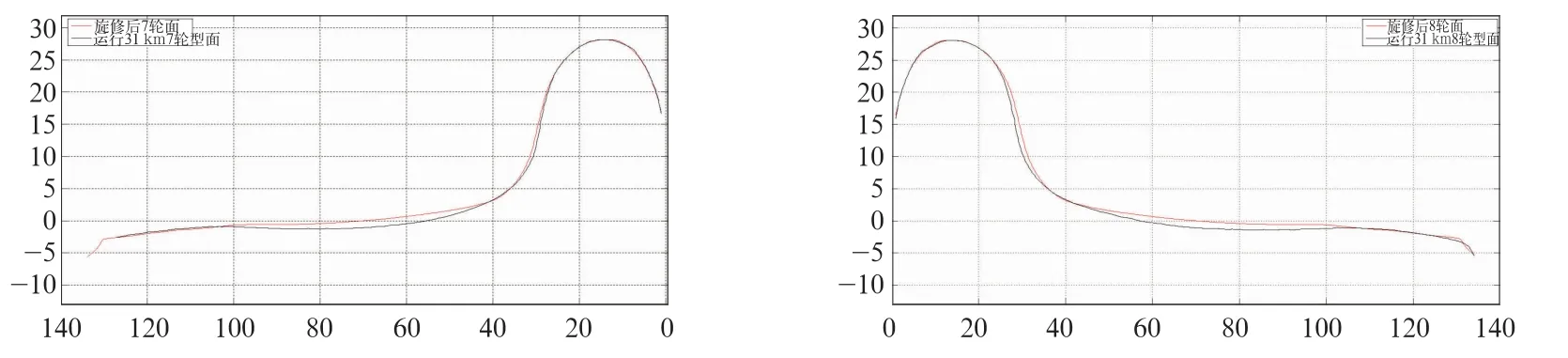
图1　Mc2车一位轮对左轮和右轮旋修后与运行31万km后实测踏面外形对比

等效锥度是轮轨接触中重要的几何参数，影响着动车组的动力学性能，若其值过小会导致动车组运用过程中出现晃车现象，其值过大会引起动车组构架横向振动报警现象［8］。轮轨接触会出现连续地磨耗现象，造成各里程对应下的等效锥度不断变化。图2（b）为轮对横移3mm处，Mc2车4个轮对等效锥度的平均值随运行里程的变化规律。由图可知：轮对横移3mm处等效锥度平均值随运行里程的增加呈现先增加后减小的趋势；该动车组运行31万km后轮对横移3mm的等效锥度平均值为0.19，在此跟踪周期内，最大值仅为0.22。参照UIC518［9］规定：速度小于等于200km/h，等效锥度λ≤0.4，等效锥度在此期间符合标准要求。由上述分析可知：在此期间等效锥度随运行里程的增加变化平缓，没有出现剧烈变化，动车组满足30万km的旋修要求。

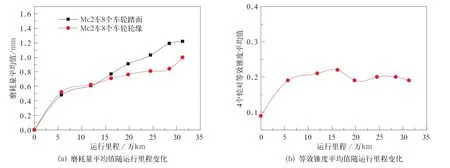
图2　磨耗量与等效锥度随运行里程变化

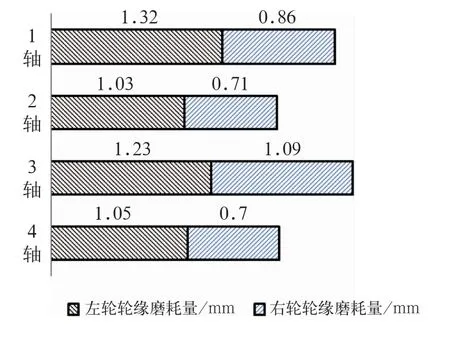
图3　Mc2车轮缘累计磨耗

在跟踪过程中发现，该动车组轮缘有偏磨现象。图3为Mc2车运行31万km之后4个车轴左轮轮缘与右轮轮缘累计磨耗量。1轴左轮轮缘与右轮轮缘磨耗量相差最大，为0.46 mm；3轴左轮轮缘与右轮轮缘磨耗量相差最小，为0.14 mm。左轮轮缘磨耗量均大于右轮轮缘磨耗量，但两者差值较小，即轮缘偏磨现象不严重。

2　接触分析

车轮与钢轨接触几何关系在跟踪周期内随着运行里程增加不断变化。选取Mc2车的一位轮对分析，旋修后和运行31万km后的车轮与钢轨轨接触关系如图4。旋修后左轮与右轮滚动圆半径相差仅为0.1mm，车轮主要在踏面滚动圆附近与轨顶内侧接触，接触点对称，分布均匀；运行31万km后左轮与右轮滚动圆半径相差为0.5mm，车轮主要在踏面滚动圆两侧与轨顶接触，且踏面滚动圆附近处接触稀疏，接触点分布不对称，说明该处形成的凹形磨耗对轮轨接触有影响。运行31万km后的车轮与钢轨接触虽没有刚旋修时接触状态好，但没有出现接触点剧烈跳跃现象，磨耗范围由踏面滚动圆附近向两侧扩大，车轮踏面磨耗趋向均匀，对提高车轮运用寿命有意义。

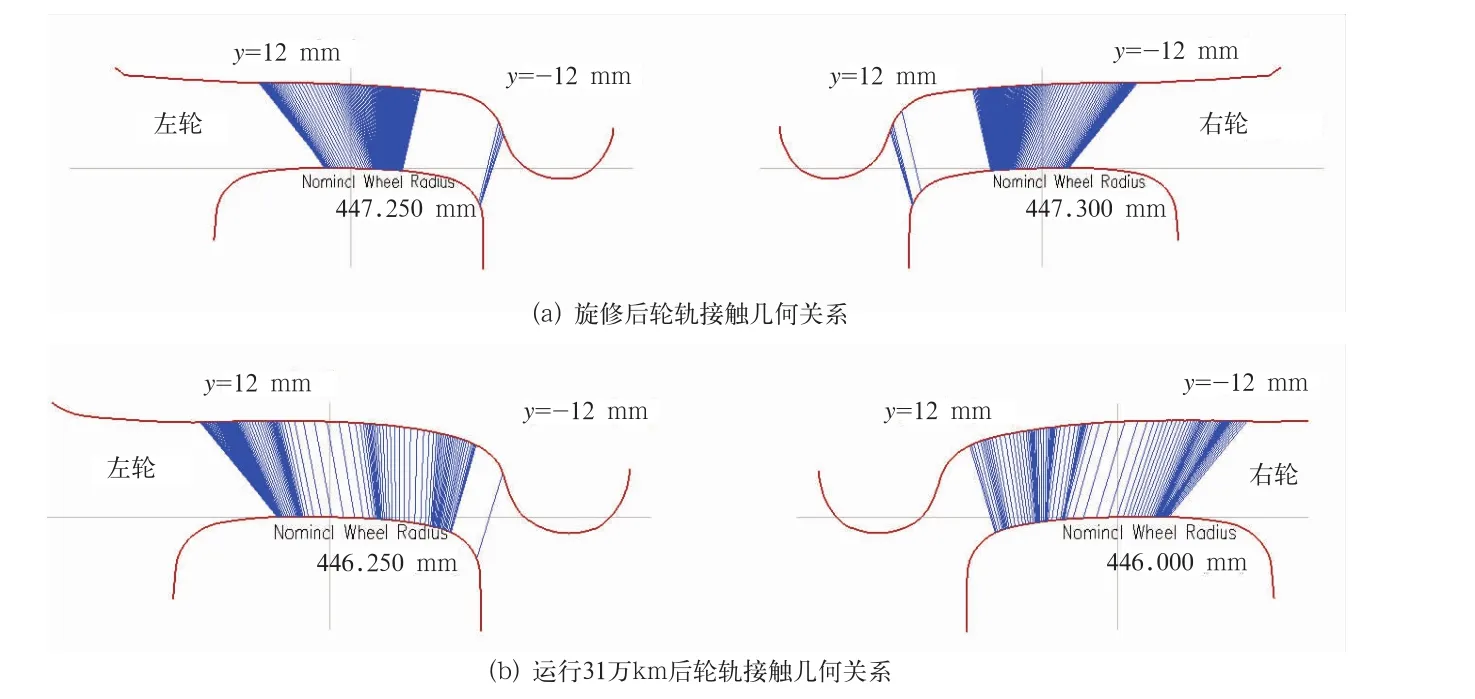
图4　Mc2车轮与钢轨接触几何关系

Mc2车一位轮对不同时期等效锥度如图5。等效锥度随轮对横移变化在不同时期呈现不同特点：旋修后，等效锥度随轮对横移变化不大，维持在0.1左右；运行31万km后，等效锥度随轮对横移增加有逐渐减小的趋势，横移大于3mm，等效锥度变化趋于平缓，但整体幅值均比旋修后大。两个时期，轮对横移3mm处等效锥度差值约为0.08，变化不剧烈，且均满足限值要求。

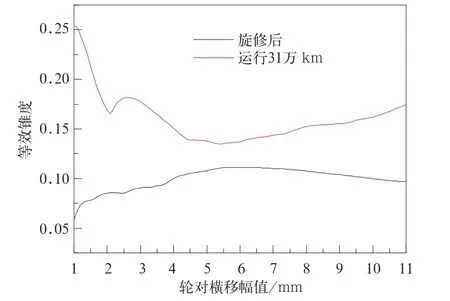
图5　Mc2车一位轮对不同时期等效锥度

3　动力学性能验证

将运行31万km的M c2车实测车轮外形输入车辆动力学模型，计算空载与重载，即M c2车不载客与定员载客两种情况下，车辆系统的稳定性、平稳性、曲线通过能力，并与相关标准［10］限值进行比较，判断动力学性能是否超标，确定磨耗后的车轮踏面是否满足车辆安全性、舒适度等要求，从而说明动车组30万km旋修周期的合理性，即动车组可以运行至30万km进行旋修。

3.1建模

采用多体动力学软件UM进行参数化建模，建立了某型动车组Mc2车。建模过程中，考虑抗蛇形减振器、横向止挡、轮轨接触的非线性，并设置如质量、质心、转动惯量等相关参数，建成由1个车体、2个转向架、4个轮对组成的动力学模型。模型包括8个一系垂向减振器、8个一系弹簧、8个定位转臂、4个空气弹簧、4个二系垂向减振器、4个二系横向减振器、2个牵引拉杆、2个横向止挡、2个抗侧滚扭杆。考虑浮沉、点头、横移、摇头、侧滚等自由度，整个系统共有48个自由度，整车动力学模型如图6。

图6　动车组Mc2车动力学模型

计算过程中，采用我国60 kg/m钢轨，并假设钢轨外形不变，德国高速轨道谱作为轨道激扰输入，轨底坡为1/40。动车组运行31万km后的实测车轮外形作为输入，并考虑左轮与右轮的轮径差，如表1。

3.2车辆系统稳定性

车辆系统的蛇行稳定性是系统本身的固有属性，是决定车辆能否高速运行的关键因素［11］。车辆系统稳定性可以通过线性临界速度与非线性临界速度进行判定。由于计算线性临界速度时，未考虑车辆系统非线性因素，其准确性受到影响，因此进行非线性分析以准确地计算车辆的临界速度。一般地，非线性临界速度的计算方法采用直接积分法，即首先让车辆在很高的速度下运行出现轮缘贴靠钢轨内侧的大幅蛇行运动，并将此状态赋给车辆系统作为初始积分状态，然后逐渐降低运行速度让其运行在理想光滑轨道上，最后当车辆系统的蛇行运动收敛至0时所对应的速度就是非线性临界速度［11］。采用此方法计算出动车组的空载与重载两种工况下不同踏面的非线性临界速度，如表2所示。重载下动车组临界速度比空载下高10 km/h左右，标准踏面的临界速度远高于已磨耗踏面临界速度。表中最恶劣工况下的临界速度为362.2 km/h，远高于该动车组运营速度200 km/ h，具有很高的安全裕量，说明动车组运行31万km之后车轮踏面状态能满足系统稳定性要求。

表1　Mc2车实测滚动圆轮径差

表2　两种踏面临界速度对比

动车组横向运行稳定性也与动车组安全性、舒适度密切相关。根据文献［10］对构架横向加速度进行了10 Hz低通滤波，计算空载与重载情况不同速度级下构架横向加速度最大值，如图7。由图7可知，空载与重载下构架横向加速度随速度变化趋势一致，重载比空载时幅值大，重载且速度为260 km/h时构架最大横向加速度为7.0 m/s-2，仍低于标准限值，且此时波形迅速收敛，转向架未失稳。因动车组实际运营速度为200 km/ h，远低于260 km/h的计算速度，所以该踏面状态下的动车组横向运行稳定性良好。

3.3车辆系统平稳性

车辆系统平稳性直接影响着乘客乘坐的舒适度。图8为动车组已运行31万km后空载与重载两种工况下，磨耗车轮踏面所对应车体平稳性、加速度RMS值随速度的变化情况。由图8（a）、图8（b）可知：随着速度的提高，车体横、垂向平稳性数值逐步增加，两者在200 km/h变化到220 km/h时增加迅速；空载与重载两种工况下，车体横向、垂向平稳性随速度的变化趋势一致，但空载下车体横向、垂向平稳性数值均高于重载工况；两种工况下，车体垂向平稳性优于车体横向平稳性，这是因为计算时没有考虑车轮不圆对车体垂向平稳性的影响。图8（a）反映：当空载速度为230 km/h、重载速度为260 km/h时，车体横向平稳性由优转向良好，但这能满足动车组以200 km/h运营时车体横向平稳性为优的要求。图8（b）反映：空载与重载下，各速度级下车体垂向平稳性均为优。图8（c）、图8（d）为车体横向、垂向加速度的RMS值随速度的变化情况，与图8（a）、图8（b）趋势近似，但随着速度的提高加速度RMS值增加较为均匀。该磨耗车轮踏面所对应的车体横向、垂向平稳性在动车组200 km/h运行时皆为优，动车组可以运行至30万km进行旋修。

图7　构架横向加速度随速度变化

3.4曲线通过能力

为了验证该磨耗踏面的曲线通过能力，设置了A、B、C、D、E、F 6种不同曲线半径的工况。曲线参数设置见表3。6种工况下，最高计算速度通过曲线时，欠超高最大为55 mm，符合《铁路工务规则》规定，即允许最大未被平衡的超高为65～75mm。

在A～E 6种工况下，计算空载与重载两种情况不同速度级下的各轮脱轨系数、轮重减载率与各轮轴横向力，并选取最大值作为统计量。

空载与重载6种工况下所对应不同速度级的最大脱轨系数如表4所示。由表4可知：6种工况下空载比重载脱轨系数大；曲线半径为400m时，空载与重载脱轨系数最大，分别为0.27，0.265，均远低于文献［10］规定的限值。各曲线所对应的速度下，脱轨系数最大时速度并不高，均在力平衡时速度以下，即此时轨道有过超高。

空载与重载6种工况下所对应不同速度级的最大轮重减载率如表5所示，与表4类似，空载时轮重减载率高于重载；B工况下，空载与重载轮重减载率最大，分别为0.66和0.61，低于文献［10］轮重减载率的动态限定值0.8，而动车组实际运营速度为200 km/h，小于工况B下240 km/h的计算速度，计算的轮重减载率具有安全裕量。

图8　车体横向与垂向平稳性、加速度RMS值随速度变化

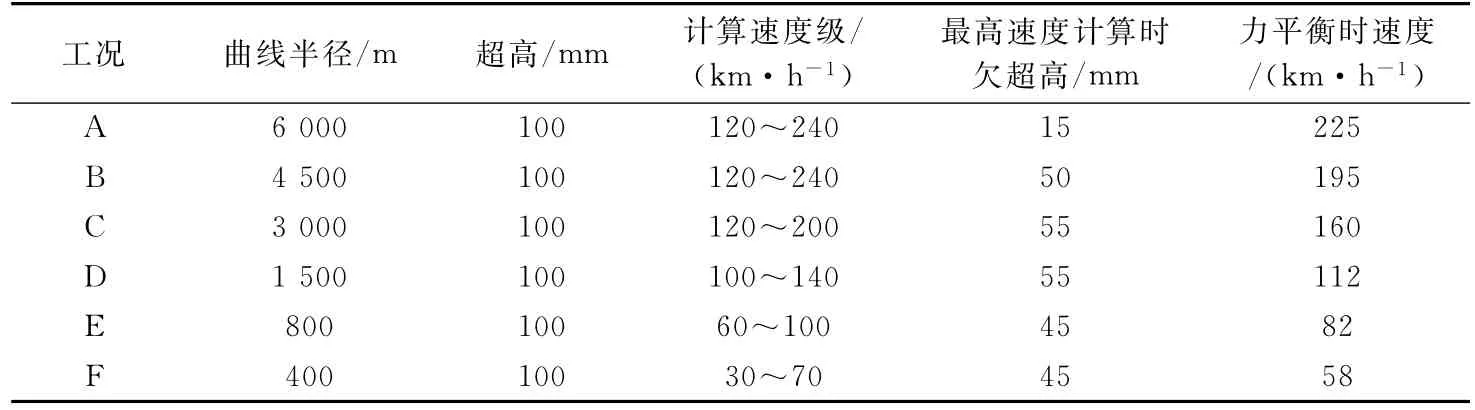
表3　曲线设置参数表

表4　6种工况下脱轨系数

表5　6种工况下轮重减载率

空载与重载6种工况下所对应不同速度级的最大轮轴横向力如表6所示，根据文献［10］计算公式（1）计算空载与重载时轮轴横向力限值分别为54，60 kN。表6显示，工况B下重载时轮轴横向力最大，为28.1 kN，低于限值；各工况下，重载时轮轴横向力较空载时大。运行31万km后的车轮踏面并没有显著影响轮轴横向力，选择30万km作为旋修周期合理。各工况下轮轴横向力最大值均出现在以最大速度或以最小速度计算时，说明欠超高与过超高均对轮轴横向力不利。

式中H为轮轴横向力，kN；P0为静轴重，kN。

表6　6种工况下轮轴横向力

表4～表6均说明运行31万km后的车轮踏面状态能满足相关动力学性能的要求，可以选择30万km作为动车组的旋修周期。

图9为所有车轮平均磨耗功率在6种工况各自速度级下的散点图。空载与重载，在各工况下，车轮平均磨耗功率随着速度的提高而增加。相同工况下，重载时车轮平均磨耗功率基本上都高于空载。相同速度级下，曲线半径越小，车轮平均磨耗功率越高，当曲线半径为400 m时，车轮磨耗最剧烈。曲线半径为400 m，速度为40 km/h时车轮平均磨耗功率高于其他工况下各速度级的车轮平均磨耗功率，曲线半径的大小显著地影响车轮磨耗功率的高低。动车组入动车运用所检修或调车时会经历半径小于400 m的曲线，所经历的小半径曲线里程占运行总里程比重小，且在实际线路上运营时，很少有半径小于800 m的曲线，车轮平均磨耗功率相对较低，车轮磨耗不剧烈。所以，动车组运行31万km后的车轮踏面状态较为理想，没有出现剧烈磨耗现象，符合实际测试情况；动车组可以运行至30万km进行旋修。

图9　6种工况下车轮平均磨耗功率

4　结 论

（1）某动车组运行31万km后，车轮踏面与轮缘磨耗、等效锥度随运行里程变化平缓，没有出现剧烈变化；左轮轮缘与右轮轮缘磨耗量差值不大，轮缘偏磨不明显；磨耗后的车轮与钢轨匹配良好，接触较为均匀。车轮磨耗状态稳定，没有出现剧烈磨耗，满足30万km旋修要求。

（2）将31万km实测车轮外形导入动力学模型计算发现：车辆系统稳定性、车体横向与垂向平稳性、过曲线能力良好，没有超过标准限值。运行31万km后磨耗车轮踏面满足动力学性能要求，动车组可以运行至30万km进行旋修。

［1］ 李 艳，张卫华，池茂儒，等.车轮踏面外形及轮径差对车辆动力学性能的影响［J］.铁道学报，2010，32（1）：104-108.

［2］ 黄照伟，崔大宾，杜 星，等.车轮偏磨对高速列车直线运行性能的影响［J］.铁道学报，2013，35（2）：14-20.

［3］ 李 艳，张卫华，周文祥.车轮型面磨耗对车辆服役性能的影响［J］.西南交通大学学报，2010，4（4）：551-554.

［4］ 董孝卿，王悦明，王林栋，等.高速动车组车轮踏面旋修策略研究［J］.中国铁道科学，2013，34（1）：88-94.

［5］ 奥山雅贵.彭惠民译.车轮踏面旋修量判定的研究［J］.彭惠民，译.国外机车车辆工艺，2009（1）：14-18.

［6］ 董孝卿，王悦明，任尊松，等.CRH3C型动车组薄轮缘车轮外形设计与运用［J］.铁道学报，2014，36（2）：11-17.

［7］ 朱韶光，董孝卿.CRH1型动车组LMD车轮外形扩大跟踪测试［R］.北京：中国铁道科学研究院机车车辆研究所，2014.

［8］ 吴 宁，董孝卿，林凤涛，等.等效锥度的计算及验证［J］.铁道机车车辆，2013，33（1）：49-52.

［9］ UIC 518.Test and approval of railway vehicles from the point of view of their dynamic behavior-Safety-Track fatigue-Ride quality［S］.International Union of Railways，2005.

［10］ 中国铁路总公司，高速动车组整车试验规范［S］.2008.

［11］ 邬平波，曾京.确定车辆系统线性和非线性临界速度的新方法［J］.铁道车辆，2000，38（5）：1-4.

［12］ 黄彩虹.高速车辆减振技术研究［D］.成都：西南交通大学，2012.

Research on the Verification of Reprofiling Cycle for EMU

DING Yangxi1，TANG Yujie1，ZHU Shaoguang2，DONG Xiaoqing3，ZHANG Xianfeng4，WANG Xianliang1
（1 East China jiaotong University，Nanchang 330013 Jiangxi，China；2 Beijing Zongheng Electro mechanical Technology Development Co.，Beijing 100081，China；3 Loco motive&car Research Institute，China Academy of Railway Sciences，Beijing 100081，China；4 Bombardier Sifang（Qingdao）Transportation Ltd.，Qingdao 266111 Shandong，China）

To verify the rationality of the reprofiling cycle in 0.3 million kilometers for an EMU，the EMU measured wheels were analyzed in the perspective of wear during the period of reprofiling cycle.Then the measured and abraded w heels profile were input to the established dynamic model of the EMU，calculated the critical speed of EMU system，EMU system frame lateral stability，the sperling index of the carbody，the dynamic performance of passing curve，and all of the calculated results were evaluated with reference to relevant standards.The results show that the wear wheel，wheel/rail equivalent conicity changes gently with the increase of running mileage，wheel-rail contact is in good state after running 0.3 million kilo meters，and the calculated dynamic performance can satisfy the requirements of standards.Finally，the rationality of the reprofiling cycle in 0.3 million kilo meters for an EMU has been verified conclusively.

reprofiling cycle；EMU；0.3 million kilometers；verification

U266.331+.1

A doi：10.3969/j.issn.1008-7842.2015.04.06

1008-7842（2015）04-0025-06

*中国铁道科学研究院科研开发基金项目（2013 YJ009）

2—）男，教授（

20215-01-12）