高速列车制动盘在不同制动工况下的残余热应力分布研究

石晓玲，李 强，赵方伟

（北京交通大学机械与电子控制工程学院，北京100044）

高速列车制动盘在不同制动工况下的残余热应力分布研究

石晓玲，李 强，赵方伟

（北京交通大学机械与电子控制工程学院，北京100044）

首先建立了残余热应力的理论模型，实测得到了锻钢制动盘材料的多线性塑性随动强化数据，并采用弹塑性有限元法模拟了高速列车制动盘在不同制动工况下的热应力和残余应力分布。主要仿真了200 km/h和300 km/h速度级下的1次紧急制动、3次200 km/h连续紧急制动及一次300 km/h紧急制动对后续常用制动的影响。结果证明制动模式是影响残余热应力分布的主要因素，工况越恶劣，残余热应力值越大；紧急制动产生的残余热应力会提高后续常用制动下应力应变响应的峰值，但后续常用制动不会影响残余热应力的值，研究成果为制动盘损伤和裂纹扩展的研究提供参考。

制动盘；热弹塑性；残余热应力；应力应变响应

构件在服役过程中，残余应力的存在会降低结构的刚度和稳定性，而且在热应力的作用下会严重影响结构的疲劳强度、抗脆断能力、高温蠕变开裂等能力［1-3］。高速列车在运行过程中发生恶劣制动（如高速紧急制动或长时坡道制动等）后制动所产生的热应力超过了材料的屈服强度，盘面将进入塑性状态，形成较高的残余拉应力，长期使用后摩擦面会产生塑性变形和微裂纹，甚至会引起制动盘的断裂、闸片的热变形和接触压力的稳定性［4］。图1为服役过程中的制动盘。观察图1发现，径向裂纹（见图1中B处）是导致制动盘失效的主要原因，龟裂纹（见图1中A处）和周向裂纹（见图1中C处）数量较少。文献［4］提出裂纹扩展的驱动力主要是残余热应力的存在。因此，研究制动过程中热应力及残余应力的分布具有重要的意义，是制动盘寿命评估和安全运营的前提和基础。

图1　制动盘及盘面裂纹

目前对制动盘瞬态温度场和应力场的研究越来越多，文献［5］研究了多次连续制动工况下制动盘的热行为，并与试验结果进行了对比分析；文献［6］研究了三维模型制动盘的温度场和应力场；文献［7］研究了单次制动下不同材料和热量分配系数对制动盘温度场的影响，但他们的研究一般都不考虑塑性变形。本文主要采用弹塑性有限元法研究了不同制动工况下的残余应力分布及该残余应力对后续制动的影响。

1　残余热应力的理论模型

当制动盘内部的温度分布发生变化时，制动盘受到结构约束而不能自由变形，则会产生热应力，如果制动过程中的热应力场超过弹性范围时盘面会发生塑性变形。假设屈服面在所有方向上均匀扩展，且初始屈服函数（开始发生塑性变形时）为Y，采用Mises屈服准则计算制动盘的热应力，如式1所示。当纯剪切的屈服应力K和应力偏张量J2相等时，材料开始屈服并产生残余应力。

制动盘在球坐标下正应力和剪应力的分量表示为：

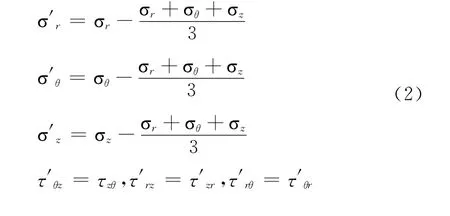
式中J2是塑性变形时制动盘内一点的应力张量的分量，可以表示为：

除了应力应变以外，制动盘还受到温度T的影响，因此，修正的Mises屈服条件可表示为：

2　锻钢材料的力学性能与弹塑性本构关系

2.1锻钢材料的力学性能试验

试验设备采用MTS-Sintech 65/G型材料试验机，试样从制动盘适当部位切取，具体尺寸如图2所示。高温试验时将试样加热到规定温度后再进行测试。试验温度分别为25℃，100℃，200℃，300℃，400℃，试验值均为3个有效试验的平均值，单调拉伸的应力应变曲线见图3。所示。

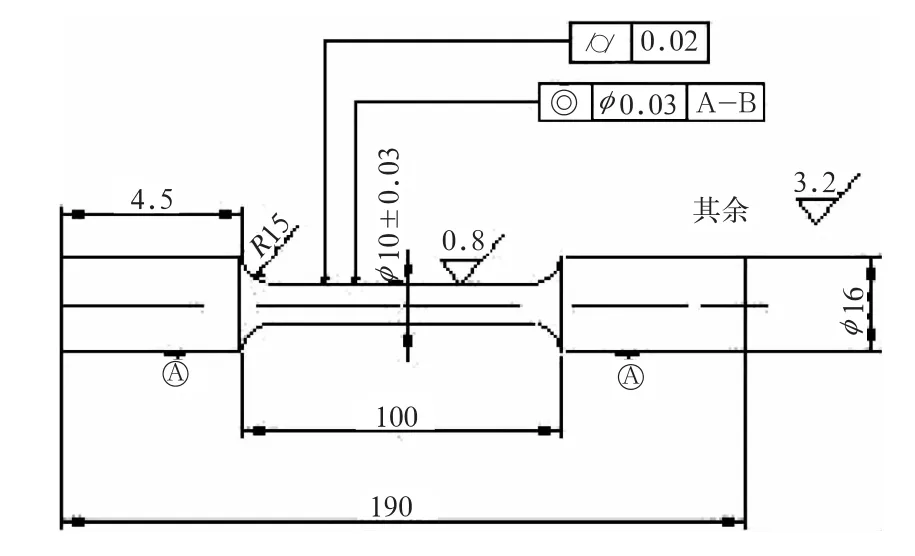
图2　常温与高温单调拉伸试样

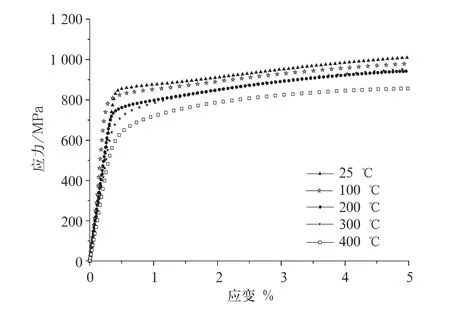
图3　单调拉伸σ—ε曲线

2.2热弹塑性本构关系

采用兰贝格—奥斯古德模型（见式5）描述其屈服点附近的应力—应变关系。利用上述常温和高温单调拉伸的试验数据，采用Matlab软件进行最小二乘法拟合锻钢材料单调拉伸应力-应变的本构模型：

式中E为弹性模量，MPa；σ为总应力，MPa；ε为弹性应变和塑性应变的总和；n和K是与材料类型相关的常数。

材料的弹性模型、屈服强度及相关参数如表1所示。从表1可以看出，材料的弹性模量和屈服强度随着温度的升高不断降低。温度越高，材料的弹性模型和屈服强度降幅越大，温度达到400℃后，材料的弹性模量仅为常温下弹性模量的0.78倍。

表1　锻钢材料的参数拟合结果

3　有限元模型与计算结果分析

3.1有限元模型及边界条件的确定

假定制动盘旋转一周的过程中速度保持不变，周围温度为20℃，采用摩擦功率法得到输入热流，制动盘的有效摩擦面积为0.21 m2，摩擦系数为0.28。在制动过程中，制动盘处于空气受迫对流散热状态，散热系数在200 km/h时取120 W/m2·℃；制动结束后，制动盘处于自然对流散热状态，取值为28 W/m2·℃，制动过程中进行线性取值。

图4制动盘的有限元模型

制动盘的有限元模型见图4。制动过程中只考虑热载荷与制动盘的相互作用。热应力计算时采用多线性等向强化准则，并利用结构分析单元SOLID185代替热分析单元SOLID70进行非线性瞬态分析。主要计算200 km/h 1次紧急制动、300 km/h 1次紧急制动，3次200 km/h紧急制动3种工况下制动盘的残余热应力分布，计算过程中对螺栓孔施加全约束。图5和图6分别为不同速度级下紧急制动的速度-时间曲线和闸片压力推力曲线。从图6可以看出，300 km/h紧急制动所承受的闸片压力大约为200 km/h的1.3倍，而制动时间为200 km/h的2倍。

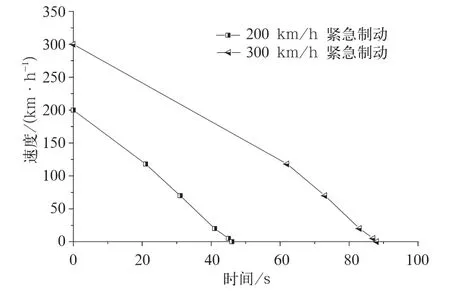
图5　不同速度级下紧急制动的速度-时间曲线

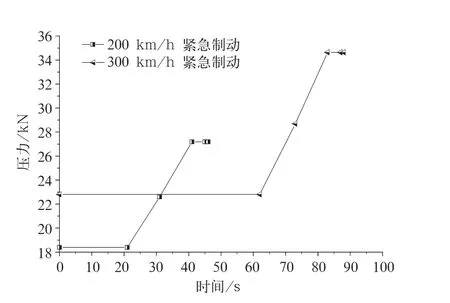
图6　不同速度级下紧急制动的压力-时间曲线

3.2不同制动工况下热应力和残余应力分析

不同制动工况下盘面径向应力、周向应力和等效应力的瞬态变化曲线如图7所示。从图7中可以看出制动盘主要承受周向应力，而径向应力较小。图1中径向裂纹和周向裂纹的数量及在制动盘上的分布也可以看出制动盘的热应力以周向应力为主。

从图7（a）可知，1次200 km/h紧急制动过程中瞬态热应力最大仅为260 MPa。3次200 km/h紧急制动（如图7（c）所示）下瞬态热应力出现了3个峰值，从图中可以发现第2个峰值比第1个峰值较高，这种变化趋势是由于第1次紧急制动热应力较小，没有塑性变形，在随后的紧急制动过程中温度越来越高，瞬态热应力也不断增大，甚至超过了材料在该温度场下的屈服强度。而第3个峰值比第2个峰值较低是因为材料的屈服强度随着温度的升高不断降低。分析1次300 km/h紧急制动（由图7（b）所示）的热应力发现该工况下弹塑性等效热应力最大，且周向的拉压应力是从450 MPa变化到-600 MPa，远远超过制动盘的疲劳极限，300 km/h紧急制动经常发生会产生破坏性裂纹而影响制动盘的安全运营。

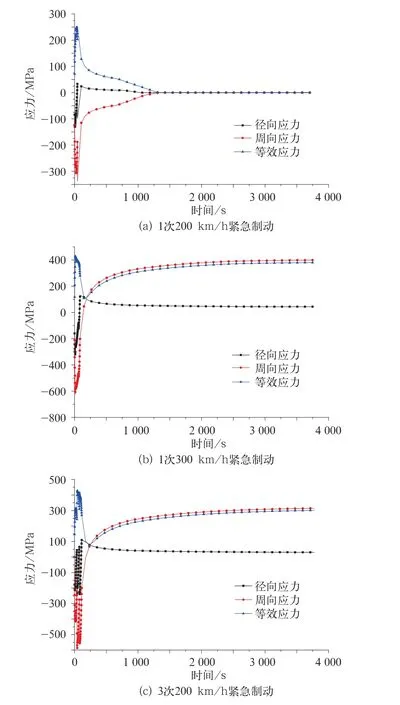
图7　不同制动工况下的摩擦环表面瞬态热应力变化曲线

当制动盘冷却到室温时，不同工况下盘面产生了不同大小的残余热应力（文中的σres均为残余热应力）。图8为3种制动工况下摩擦面的应力应变响应。箭头代表制动过程中应力应变响应的变化趋势。由图8可知，1次200 km/h紧急制动在制动结束后应力应变又回到了初始位置，所以该工况没有生成残余应力；1次300 km/h紧急制动和3次连续紧急制动，在弹性阶段盘面的等效应力与应变呈现线性关系，盘面屈服后等效应力基本不变而应变不断增加，制动结束后随着弹性应变的消失，等效应力也不断减小。但制动盘在散热过程中，盘面比内部冷却快使表面形成了残余拉应力，内部冷却较慢形成了残余压应力，制动结束后盘面应力有一段反向增加的过程，该过程与制动开始时应力增加的过程平行。1次300 km/h紧急制动生成了380 MPa的残余应力，3次200 km/h紧急制动的残余应力达到了293 MPa。

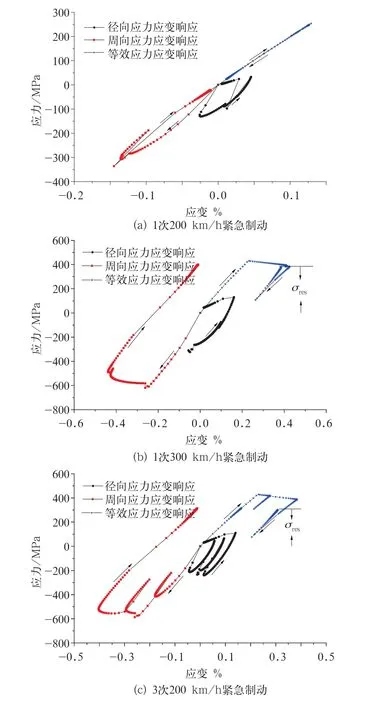
图8　不同制动工况下的摩擦环表面应力应变响应

从这一规律可以看出制动模式是影响热应力和残余热应力分布的主要因素。制动工况越恶劣，盘面温度梯度越大，生成的残余拉应力也越大。1次300 km/h紧急制动和3次200 km/h连续紧急制动形成的残余热应力甚至可能诱导盘面生成裂纹，高速列车在运行过程中应极力避免这些工况的发生。

等效残余应力沿制动盘厚度方向的分布见图9，研究发现距离摩擦面越远，残余应力越小。300 km/h紧急制动的最大残余应力380 MPa，文献［8］中采用X射线应力测定仪测定了270 km/h下一次紧急制动的残余应力发现摩擦面最中间的残余热应力最大，为348.4 MPa，与本文的有限元仿真结果基本吻合，说明了三维有限元仿真结果的有效性。

图9　等效残余应力沿制动盘厚度方向的分布

3.3残余热应力对后续制动的影响

高速列车在运行过程中主要以常用制动为主，为了研究残余应力对后续常用制动的影响，对制动盘进行1次300 km/h紧急制动后再进行两次200 km/h的常用制动。每次制动结束后盘面都降到常温。图10为该工况下的应力应变响应曲线。

从图10可以看出，300 km/h紧急制动结束后形成了残余拉应力，但随后的两次常用制动都在残余拉应力的基础上循环且不会影响原来残余拉应力的值。第1次常用制动过程中随着温度的升高，盘面形成了残余压应力，与原来的残余拉应力中和而减小，降到室温后残余拉应力的值又回到紧急制动结束时的状态。第2次常用制动基本沿着第1次的轨迹变化。因此，残余拉应力的存在会提高后续常用制动过程中的应力应变响应的峰值。残余拉应力与后续制动过程中的压应力一起组成了拉压循环，驱动制动盘裂纹的形成和扩展。

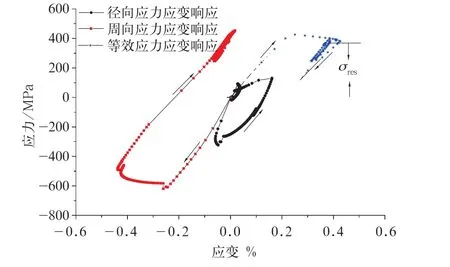
图10　1次紧急制动后再进行两次常用制动下的应力应变响应

4　结 论

（1）采用弹塑性有限元法对高速列车制动盘在不同工况下的热应力和残余应力进行了数值模拟分析。经过对比发现有限元结果和试验结果基本吻合，说明了有限元结果的有效性；

（2）制动盘热应力和残余应力的计算结果表明：热残余应力的值主要取决于制动工况。制动工况越恶劣，制动盘的残余热应力值越大。

（3）残余热应力的存在会提高后续常用制动过程中应力应变响应回线的峰值点和谷值点，但该值不会随着常用制动次数而变化。

［1］ 周继承，黄伯云.列车制动摩擦材料研究进展［J］.材料科学与工程，1997，17（3）：91-93.

［2］ JI-Hoon Choi.Finite Element Analysis of Transient Therm o-elastic Behaviors in Disk Brakes［J］.Wear，2004，257（9）：47-58.

［3］ M.M.Shahzmanian.Transient and Thermal Contact A-nalysis for the Elastic Behavior of Functionally Graded Brake Disks due to Mechanical and Thermal Loads［J］. Materials and Design 2010，31（10）：4655-4665.

［4］ 杨月，谢基龙.高速客车SiCp/A356铝基制动盘材料的热疲劳裂纹形成与扩展试验研究［J］.铁道学报，2007，29（5）：43-47.

［5］ Monica Siroux.Thermal A nalysis of Periodic Sliding Contact on a Braking Tribometer［J］.Applied Thermal Engineering，2008，28（17-18）：2194-2202.

［6］ 丁群，谢基龙.基于三维模型的制动盘温度场和应力场计算［J］.铁道学报，2002，24（6）：34-38.

［7］ Adam Adamowicz.Three-dimensional FE model for calculation of temperature of a thermosensitive disc［J］.Applied Thermal Engineering，2013，50（1）：572-581.

［8］ 李继山，韩晓辉.高速列车制动盘残余热应力数值仿真及试验验证［J］.铁道机车车辆，2010，30（6）：8-10.

Research on Residual Thermal Stress of High Speed Train Brake Disk under Different Braking Conditions

SHI Xiaoling，LI Qiang，ZHAO Fangwei
（School of Mechanical，Electronic and Control Engineering，Beijing Jiaotong University，Beijing 100044，China）

A theoretical model for residual thermal residual stress is established and the multi-linear kinematic hardening plasticity of material is obtained through measurement.In different braking conditions，the residual stress distribution and thermal stress distribution of brake disc is simulated using elastic-plastic finite element method.The emergency braking（200k m/h and 300k m/h），three emergency braking（200k m/h）and residual stress of two successive services braking after an emergency braking are simulated under 300k m/h.Research shows that the main factors affecting the residual thermal stress is braking mode.Under critical conditions，the residual thermal stress is greater.The peak value and valley value of subsequent stress-strain response are rising due to residual stress caused by the emergency braking.And the residual stress won＇t change in subsequent service braking.The research results provide reference for brake disc damage and crack propagation.

brake disc；thermal elastic-plastic；residual thermal stress；stress and strain response

U292.91+4 U260.351

A doi：10.3969/j.issn.1008-7842.2015.04.02

1008-7842（2015）04-0007-04

5—）女，博士研究生（

2014-12-17）