一些几何不等式的等价关系

袁淑峰，金海林

（1.上海大学理学院，上海 200444；2.绍兴文理学院上虞分院，浙江上虞 312300）

一些几何不等式的等价关系

袁淑峰1，2，金海林1

（1.上海大学理学院，上海 200444；2.绍兴文理学院上虞分院，浙江上虞 312300）

Brunn-Minkowski不等式和Minkowski不等式是凸几何中的两个重要而基本的不等式.近期，已有学者得到了这两个不等式的Orlicz版本，从而构建起Orlicz-Brunn-Minkowski理论的框架.本工作证明经典的Brunn-Minkowski不等式、Minkowski不等式、Orlicz-Brunn-Minkowski不等式和Orlicz-Minkowski不等式是等价的.

Brunn-Minkowski不等式；Minkowski不等式；Minkowski和；Orlicz和；均质积分

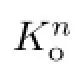
几何不等式的等价性一直是凸几何分析的重点研究对象［1-2］.Brunn-Minkowski不等式和Minkowski不等式作为Brunn-Minkowski理论中的两个重要而基本的不等式，一直受到广泛的关注.

经典Minkowski不等式［3-4］描述如下：

如果凸体K，L∈Kn，则有

等号成立当且仅当K和L是位似的.

经典Brunn-Minkowski不等式［5］描述如下：如果凸体K，L∈Kn，则有

等号成立当且仅当K和L是位似的.式（2）中，K+L表示凸体K和L的Minkowski和.

令Φ2表示定义在［0，∞）2→［0，∞）上的凸函数φ的集合.凸函数φ对于两个变量都是单调递增的，且有φ（0，0）=0和φ（0，1）=φ（1，0）=1.

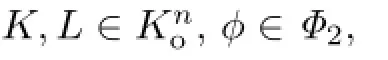
近期，Gardner等［6］给出了关于Orlicz和的Brunn-Minkowski不等式以及Orlicz-Minkowski不等式.

如果凸体K，L∈Kno，φ∈Φ2，那么Orlicz-Brunn-Minkowski不等式表示为

式中，如果φ是严格凸的，等号成立当且仅当K和L是互为伸缩的.

式中，如果φ是严格凸的，等号成立当且仅当K和L是互为伸缩的.

本工作主要是证明上述4个不等式（式（1）～（4））的等价关系.

1　预备知识

令Sn-1表示Rn中质心在原点的单位球B的表面，h（K，·）=hK（·）：Sn-1→R表示凸体K∈Kn的支撑函数，即

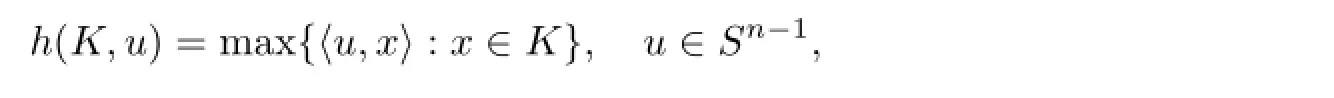
式中，〈u，x〉表示u和x在Rn上的通常内积.

凸体K的径向函数ρ（K，·）：Sn-1→R定义为ρ（K，u）=max｛λ＞0：λu∈K｝，u∈Sn-1.若凸体K，L满足ρ（K，·）/ρ（L，·）：Sn-1→R是常数，则称K和L是互为伸缩的.对于凸体K，L，若存在常数a＞0，b∈Rn，使得K=aL+b成立，则称凸体K和L是位似的.

对于Rn中的凸体K和L，若u∈Sn-1，则它们的Minkowski和K+L［4］定义为

如果p≥1，凸体K，L包含原点且原点在其内部，对于u∈Sn-1，凸体K+pL通过支撑函数定义为

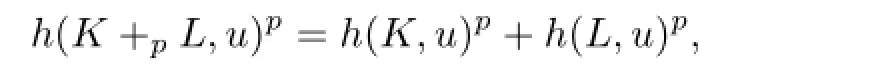
式中，称运算+p为Firey p-和［7］.目前，Firey p-和已被Lutwak等［8］推广到任意非凸集.

若凸体K，L∈Kno，φ∈Φ2，任意向量u∈Rn，则对于凸体K和L的Orlicz和K+φL，很容易得到hK+φL（u）=λ（u）的必要条件为

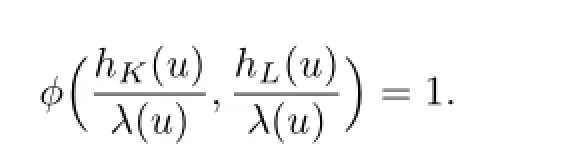
当φ（x，y）=φ1（x）+φ2（y），φ1，φ2∈Φ时，则有

当φ（x，y）=xp+yp，1≤p＜∞时，Orlicz和变成Firey p-和；而当φ（x，y）=max｛x，y｝时，凸体K和L的Orlicz和就变成K和L的并的凸包.

均质积分是混合体积的一个重要的例子［4］.如果K是Rn中的一个紧凸集，0≤i≤n，那么K的均质积分Wi（K）定义为Wi（K）=V（K，n-i；B，i），则W0（K）=V（K）（K的体积），nW1（K）=S（K）（K的表面积），Wn（K）=V（B）=ωn（单位球的体积）.

如果凸体K，L∈Kn，0≤i≤n-1，则K，L的混合均质积分Wi（K，L）［9-10］定义为

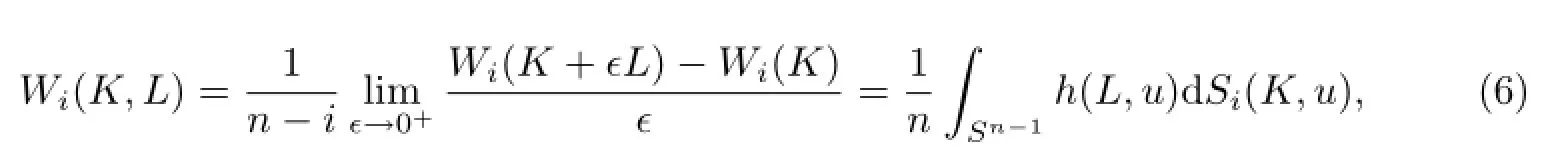
式中，Borel测度Si（K，·）是K的i次表面积测度.由于Wi（λK）=λn-iWi（K），则对于所有的i，可得到Wi（K，K）=Wi（K）.

如果凸体K，L∈Kno，0≤i≤n-1，且p≥1，那么凸体K，L的混合p-均质积分Wp，i（K，L）［11］定义为

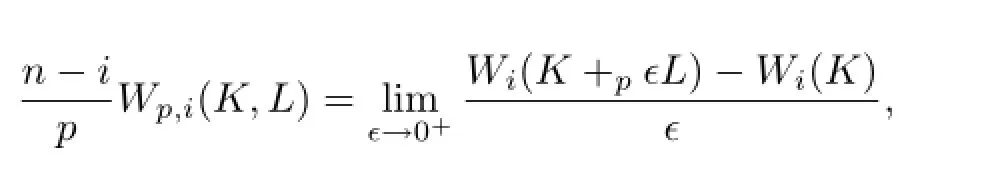
如果p=1，那么Wp，i（K，L）=Wi（K，L），显然有Wp，i（K，K）=Wi（K）.

假设µ是X空间中的一个概率测度，g：X→I⊂R是一个µ-可测函数，其中I可能是一个无界区间.Jensen不等式表述为如果ϕ：I→R是一个凸函数，那么

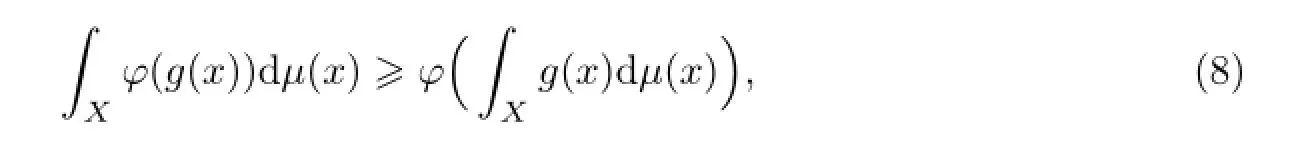
如果ϕ是严格凸的，等号成立的充要条件是对于X中的每个x几乎处处µ-可测的函数g（x）是一个常数函数［12］.

2　定理的证明

下面建立相对于定理1的更广泛的均质积分形式，并给出详细的证明.

1993年，Lutwak［11］证明了Lp-Minkowski不等式的均质积分形式.若p≥1，凸体K，L∈Kn，0≤i≤n-1，则

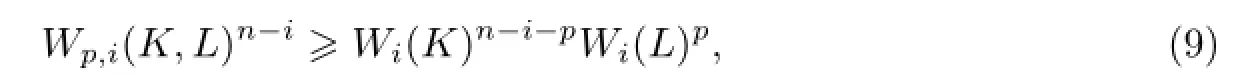
当p＞1时，等号成立当且仅当K和L是互为伸缩的.

若取p=1，则式（9）变为经典Minkowski不等式的均质积分形式［9-10］：

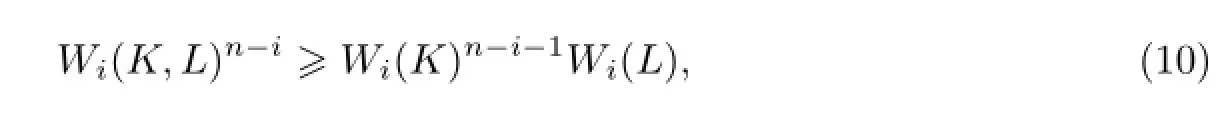
等号成立当且仅当K和L是位似的.

Firey［7］证明了下列关于Firey p-和的Lp-Brunn-Minkowski不等式的均质积分形式.若p≥1，凸体K，L∈Kn，0≤i≤n-1，则

当p＞1时，等号成立当且仅当K和L是互为伸缩的.

若取p=1，则式（11）变为经典Brunn-Minkowski不等式的均质积分形式：

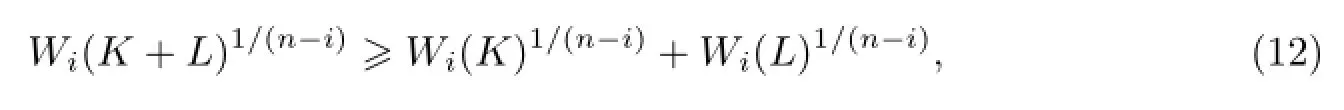
等号成立当且仅当K和L是位似的.

Orlicz-Minkowski不等式和Orlicz-Brunn-Minkowski不等式的均质积分形式如下.

如果φ是严格增的，等号成立当且仅当K和L是互为伸缩的.

如果φ是严格增的，等号成立当且仅当K和L是互为伸缩的.

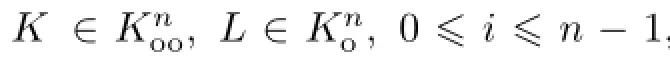
当φ严格凸时，等号成立当且仅当K和L是互为伸缩的.

证明根据式（5）～（7）和式（13），可得

如果φ是严格凸的，那么φ1和φ2也是严格凸的，于是根据式（13）的等号成立条件，可得到凸体K，L分别与K+φL是互为伸缩的，所以K和L也是互为伸缩的.

在定理2中，若取i=0，就得到了Gardner等［5］给出的结论.

当φ严格凸时，等号成立当且仅当K和L是互为伸缩的.

已知经典Brunn-Minkowski不等式和Minkowski不等式的均质积分形式是等价的，因此可得如下引理.

引理1［11］如果凸体K，L∈Kn，0≤i≤n-1，则有

等号成立当且仅当K和L是位似的.

在定理2中，若取φ（x，y）=φ1（x）+φ2（y）=x+y，就可得到引理1的部分结论.

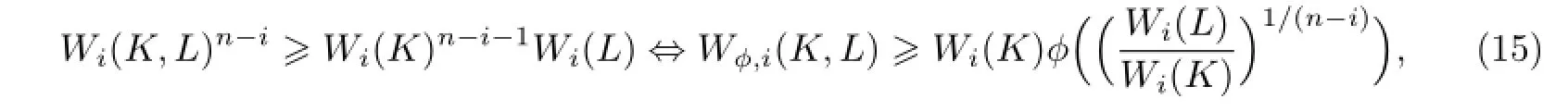
如果φ是严格凸的，那么不等式等号同时成立当且仅当K和L是互为伸缩的.

证明“⇒”因为

“⇐”取φ（t）=t，易证得结论.

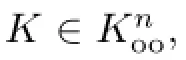
如果φ是严格凸的，那么不等式等号同时成立当且仅当K和L是互为伸缩的.

证明在式（14）中取φ（x，y）=φ1（x）+φ2（y）=x+y，即可得到经典Brunn-Minkowski不等式的均质积分形式：

根据引理1和引理2，易得所需的推导关系.

根据式（15）、引理1和引理2的等号成立条件可知，当φ严格凸时，定理3中的等号成立当且仅当K和L是互为伸缩的.结合定理2和定理3，可得到如下定理.

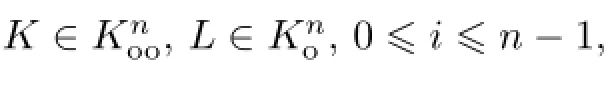
当φ严格凸时，等号成立当且仅当K和L是互为伸缩的.

在定理4中，当i=0，φ（x，y）=φ1（x）+φ2（y）时，可以发现Orlicz-Minkowski不等式和Orlicz-Brunn-Minkowski不等式是等价的，并有如下推论.

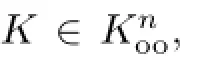
当φ严格凸时，等号成立当且仅当K和L是互为伸缩的.

在定理4中，若取i=0，φ（x，y）=xp+yp，p≥1，可得到Lp-Brunn-Minkowski不等式和Lp-Minkowski不等式的等价性.

推论3［2］如果凸体K，L∈Kno，p≥1，那么

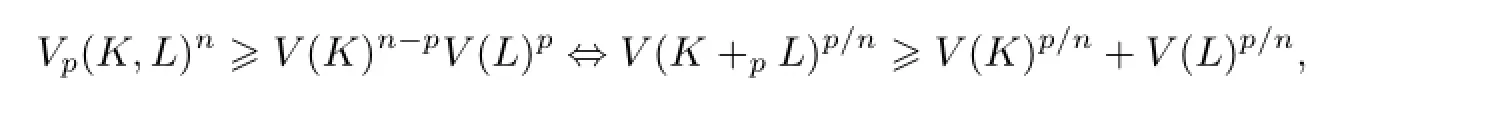
等号成立当且仅当K和L是互为伸缩的.

根据定理2、引理1、引理2和定理3，可以得到如下定理.

当φ∈Φ2且φ（x，y）=φ1（x）+φ2（y），φ1，φ2∈Φ时，式（3）可变为

如果φ是严格凸的，等号成立当且仅当K和L是互为伸缩的.

由定理5可以看出，当i=0时，定理5就转化为定理1.

［1］虞志刚，袁俊，冷岗松.Lp投影不等式和Lp质心不等式的等价性［J］.上海大学学报：自然科学版，2009，15（1）：8-10.

［2］赵长健，冷岗松，李小燕.凸体几何一些经典不等式的等价性［J］.数学学报，2005，48（2）：347-354.

［3］Gardner R J.Geometric tomography［M］.2nd ed.New York：Cambridge University Press，2006.

［4］Schneider R.Convex bodies：the Brunn-Minkowski theory［M］.Cambridge：Cambridge University Press，1993.

［5］Osserman R.The isoperimetric inequality［J］.Bull Amer Math Soc，1978，84（6）：1182-1238.

［6］Gardner R J，Hug D，Weil W.The Orlicz-Brunn-Minkowski theory：a general framework，additions，and inequalities［J］.J Differential Geom，2014，97（3）：427-476.

［7］Firey W J.p-means of convex bodies［J］.Math Scand，1962，10：17-24.

［8］Lutwak E，Yang D，Zhang G Y.TheBrunn-Minkowski-Fireyinequality for non-convex sets［J］. Adv in Appl Math，2012，48（2）：407-413.

［9］Busemann H.Convex surfaces［M］.New York：Interscience Publishers，1958.

［10］Leichtwei K.Konvexe mengen［M］.Berlin：Springer-Verlag，1980.

［11］Lutwak E.The Brunn-Minkowski-Firey theory I：mixed volumes and the Minkowski problem［J］.J Differental Geom，1993，38（1）：131-150.

［12］Hoffmann-Jorgensen J.Probability with a view toward statistics［M］.New York：Chapman and Hall，1994.

［13］Burago Y D，Zalgaller V A.Geometric inequalities［M］.Berlin：Springer-Verlag，1998.

Equivalence properties of some geometric inequalities

YUAN Shu-feng1，2，JIN Hai-lin1
（1.College of Sciences，Shanghai University，Shanghai 200444，China；2.Shangyu Branch，Shaoxing University，Shangyu 312300，Zhejiang，China）

Brunn-Minkowski inequality and Minkowski inequality are two important and fundamental inequalities in convex geometric analysis.Recently，some researchers established Orlicz extension of these two inequalities，and constructed a general framework for the Orlicz-Brunn-Minkowski theory.The purpose of this paper is to show equivalence properties of these four inequalities，i.e.，classical Brunn-Minkowski inequality，classical Minkowski inequality，Orlicz-Brunn-Minkowski inequality and Orlicz-Minkowski inequality.

Brunn-Minkowski inequality；Minkowski inequality；Minkowski addition；Orlicz addition；Quermassintegral

O 186.5

A

1007-2861（2015）06-0725-07

10.3969/j.issn.1007-2861.2014.01.043

2014-03-04

国家自然科学基金资助项目（11271244）；浙江省教育厅科研基金资助项目（Y201328555）

袁淑峰（1976—），女，副教授，博士，研究方向为凸几何.E-mail：yuanshufeng2003@163.com