混合AKNS-CLL方程的N-孤子解
潘红飞,夏铁成
(上海大学理学院,上海 200444)
混合AKNS-CLL方程的N-孤子解
潘红飞,夏铁成
(上海大学理学院,上海 200444)
由Hirota方法推导出混合AKNS-CLL方程的双线性导数方程和N-孤子解,并比较混合AKNS-CLL方程、AKNS方程和CLL方程的单孤子解|q|和|r|的图像,可以发现混合AKNS-CLL方程的特征形状不同于经典AKNS和CLL方程解.最后,通过约化,得到混合非线性Schr¨odinger方程的N-孤子解.
混合AKNS-CLL方程;混合非线性Schr¨odinger方程;N-孤子解;Hirota方法
非线性Schr¨odinger方程是非线性波理论研究所关注的一个问题.这一类方程的物理背景来源于非线性光学、非线性水波和等离子物理学等[1-4].许多Schr¨odinger方程的精确解可以通过Hirota双线性法、反散射变换法、Jacobi椭圆法、tanh函数法等方法获得[5-8],Schr¨odinger方程的多分量和超可积情形也是当前研究的热点[9-11].
本工作考虑如下混合AKNS-CLL方程:

式中,q=q(x,t),r=r(x,t)是关于x和t的复函数,a,b∈C.当a=1,b=0和a=0,b=1时,方程(1)分别对应于二阶等谱AKNS方程[12-13]和带导数的非线性Schr¨odinger方程[14-15].当r=q∗时,令t为-it,x为ix,则方程(1)约化为混合非线性Schr¨odinger方程(combined nonlinear Schr¨odinger equation,CNSE),即
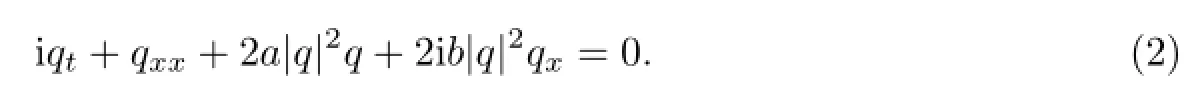
1 双线性形式和N-孤子解
令

并利用恒等式
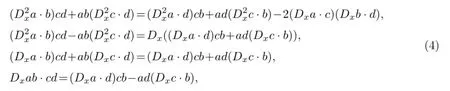
则方程(1)转化为双线性导数方程:

式中,D是Hirota双线性算子,定义为

为求出混合AKNS-CLL方程(1)的N-孤子解,将f,g,s,h按参数ε展成级数,则有
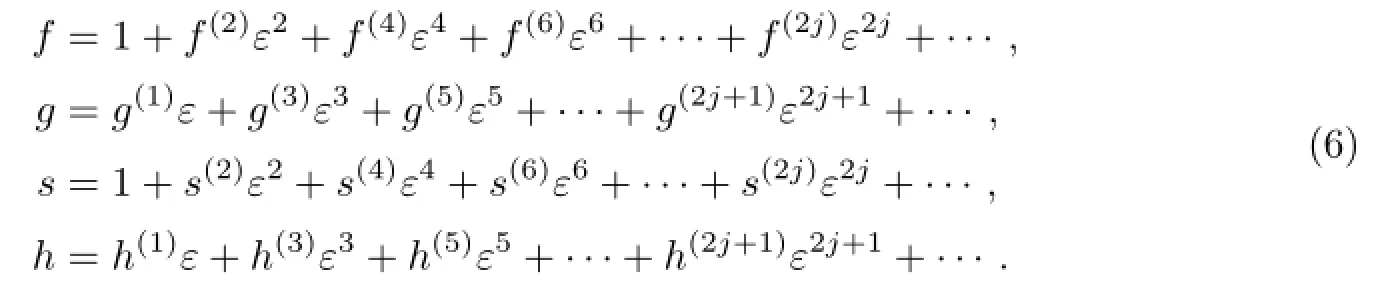
将式(6)代入方程(5),并比较ε的同次幂系数,可得


由式(7)和(8)可知,g(1)和h(1)有如下线性指数函数形式的解:
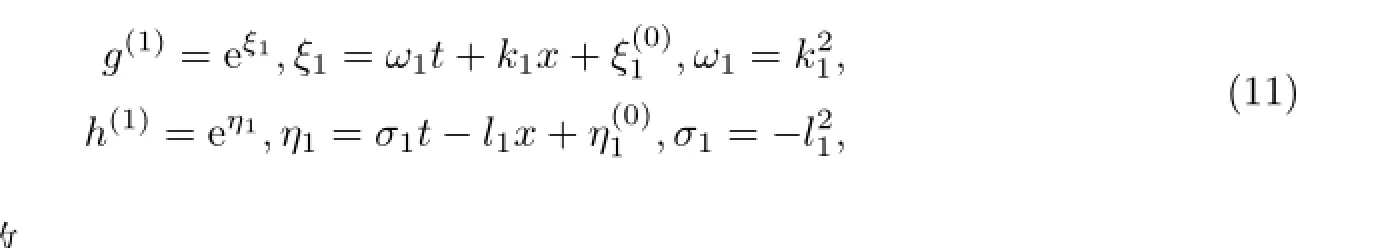

由式(3),可推得当ε=1时方程(1)的单孤子解为
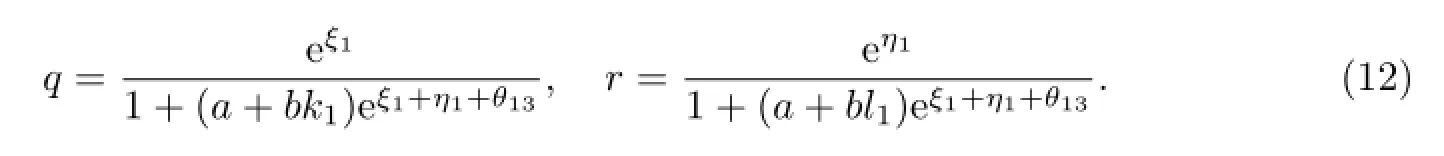
特别地,当(a,b)=(1,0)时,式(12)为二阶等谱AKNS方程的单孤子解[13];当(a,b)=(0,1)时,式(15)为带导数的非线性Schr¨odinger方程的单孤子解[16].作为对比,本工作给出由式(12)决定的|q|和|r|在4种情形时的图像(见图1).通过选择不同的参数k1,l1,可以发现混合AKNS-CLL方程有类似于尖孤子解(peakon soliton)的性态(见图1(d)),这种现象是单一AKNS方程或CLL方程所不具有的一类特性.AKNS-CLL方程与AKNS方程、CLL方程存在本质的区别.
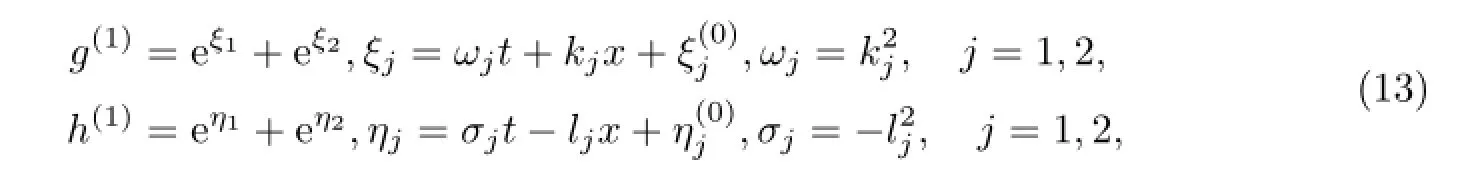


图1 方程(1)的单孤子解Fig.1 One soliton solutions of Eq.(1)
将式(13)代入式(9)和(10),可得
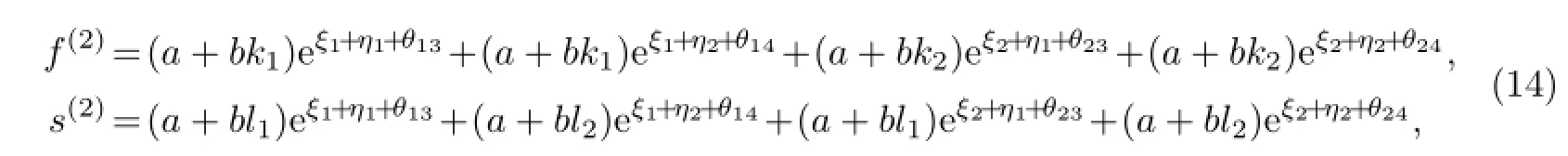
将式(13)和(14)代入式(7)和(8)的第二式,有
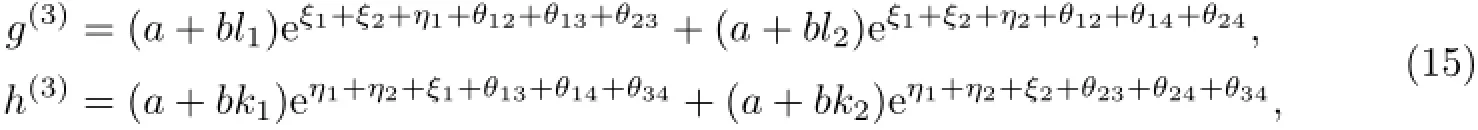
将式(13)~(15)代入式(9)和(10)的第二式,又可得到
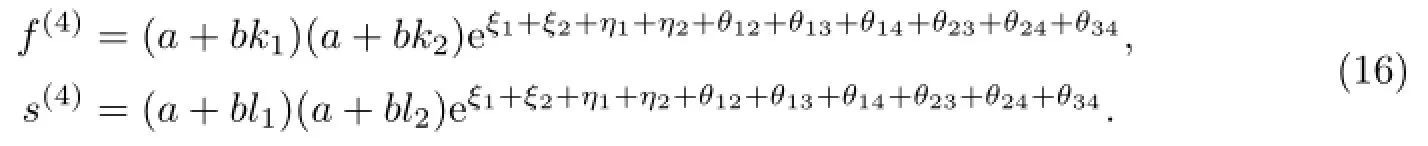
根据式(7)~(10),可取

所以,有

因此,令ε=1,即可求得方程(1)的双孤子解(见式(3)).特别地,当(a,b)=(1,0)时,可引出二阶等谱AKNS方程的双孤子解[13];当(a,b)=(0,1)时,可求得带导数非线性Schr¨odinger方程的双孤子解[16].
一般地,方程(1)的关于f,g,h和s的N-孤子解(N=1,2,···)为
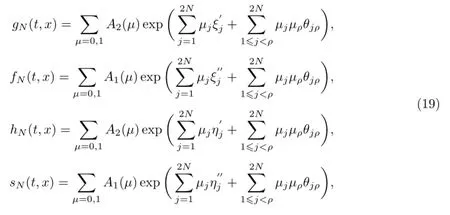
式中,
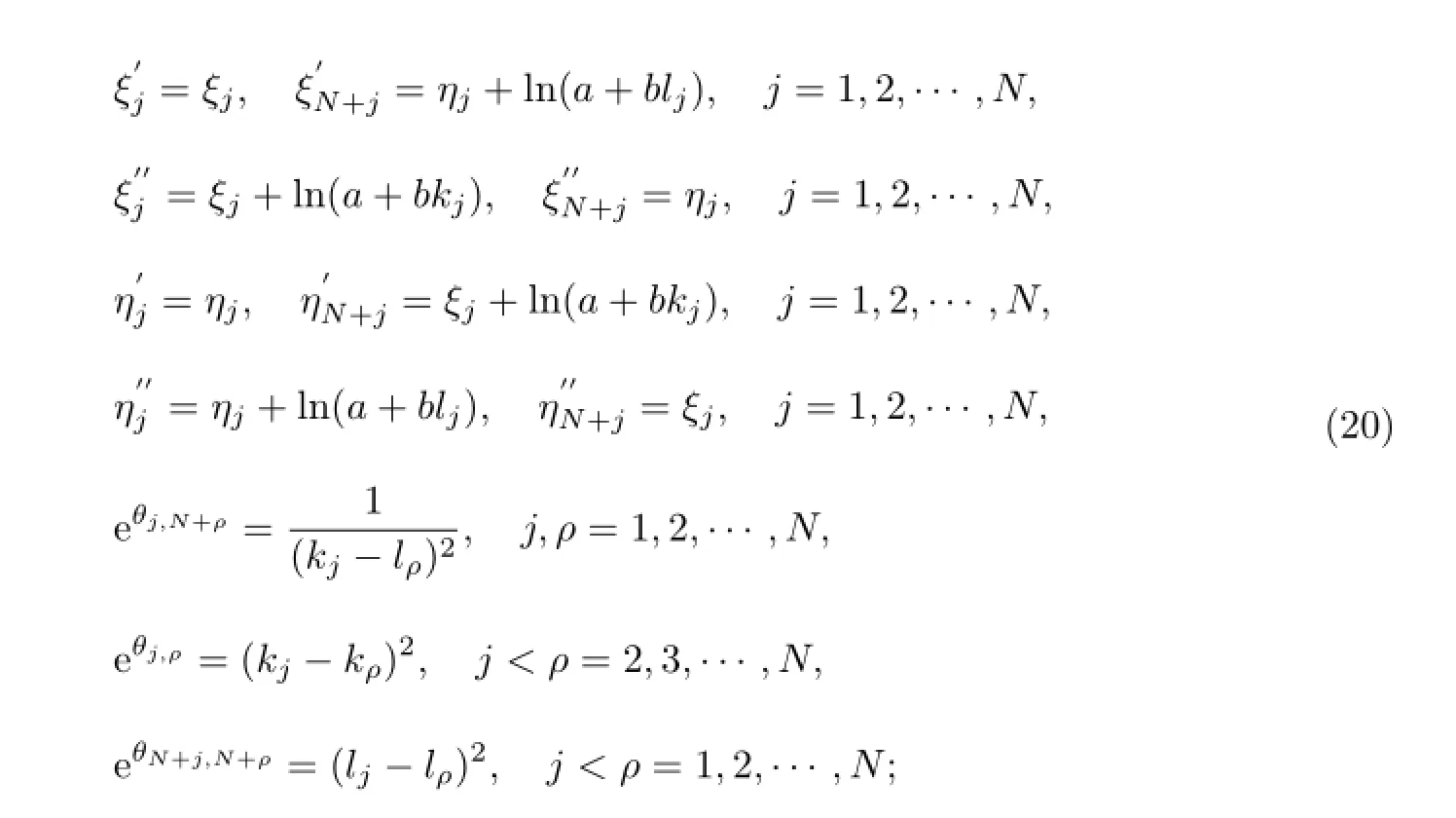
A1(µ),A2(µ)表示当µj(j=1,2,···,2N)取所有可能的0或1时,还需分别满足

2 约化
作为应用,考虑混合非线性Schr¨odinger方程(式(2)),并通过方程(1)的约化给出双线性导数方程和N-孤子解.取s=f∗,h=g∗,并令t为-it,x为ix,则方程(4)约化为式(2)的双线性导数方程,即

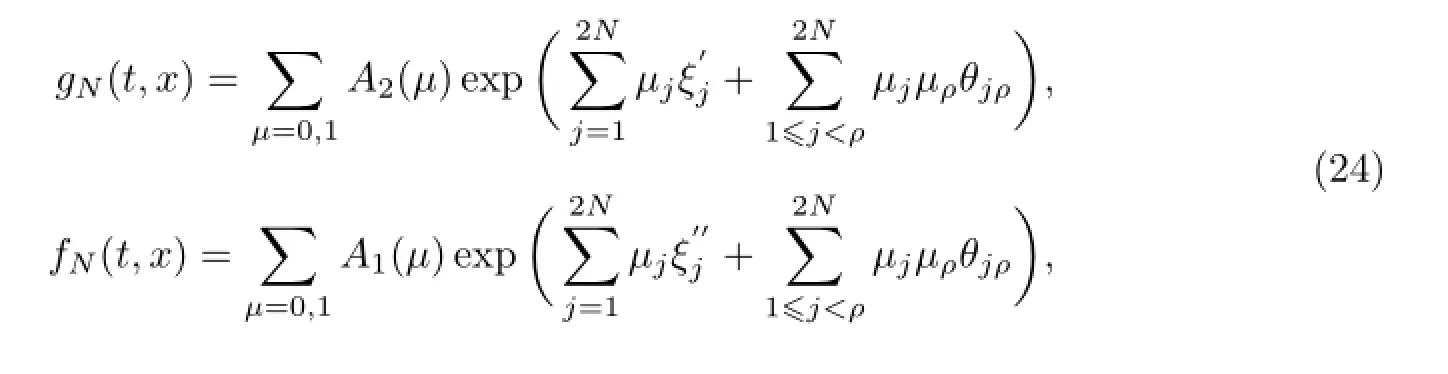
式中,

致谢感谢上海大学数学系陈登远教授的有益指导.
[1]Johnson R S.A modern introduction to the mathematical theory of water waves[M].New York:Cambridge University Press,1997:298-345.
[2]Belashov V Y,Vladimirov S V.Solitary wave in dispersive complex media[M].Berlin:Springer-Verlag,2005.
[3]Kivshar Y S,Agrawal G P.Optical solitons from fibers to photonic crystals[M].New York:Academic Press,2003:3-25.
[4]Maimistov A I.Solitons in nonlinear optics[J].Quantum Electronics,2010,40:756-781.
[5]Zayed E M E,Zedan H A,Gepreel K A.On the solitary wave solutions for nonlinear Hirota-Satsuma coupled KdV of equations[J].Chaos,Solitons and Fractals,2004,22(2):285-303.
[6]Khuri S A.A complex tanh-function method applied to nonlinear equations of Schr¨odinger type[J].Chaos,Solitons and Fractals,2004,20(5):1037-1040.
[7]Ablowitz M J,Clarkson P A.Solitons,nonlinear evolution equations and inverse scattering[M].Cambridge:Cambridge University Press,1991:70-100.
[8]Hirota R.The direct methods in soliton theory[M].Cambridge:Cambridge University Press,2004:157-168.
[9]Tsuchida T,Wadati M.New integrable systems of derivative nonlinear Schr¨odinger equations with multiple components[J].Physics Letter A,1999,257:53-64.
[10]Roelofs G H M,Kersten P H M.Supersymmetric extensions of the nonlinear Schr¨odinger equation:symmetries and coverings[J].Journal of Mathematical Physics,1992,33(6):2185-2206.
[11]He G L,Zhai Y Y,Geng X G.A super hierarchy of coupled derivative nonlinear Schr¨odinger equations and conservation laws[J].Communications in Nonlinear Science and Numerical Simulation,2014,19(7):2228-2233.
[12]Chen D Y,Zhang D J,Bi J B.New double Wronskian solutions of the AKNS equation[J]. Science China Mathematics,2008,51(1):55-69.
[13]Ablowitz M J,Kaup D J,Newell A C,et al.The inverse scattering transform-Fourier analysis for nonlinear problem[J].Studies in Applied Mathematics,1974:53(4):249-315.
[14]Chen H H,Lee Y C,Liu C S.Integrability of nonlinear Hamiltonian systems by inverse scattering method[J].Physica Scripta,1979,20:490-492.
[15]Chen D Y.k-constraint for the modified Kadomtsev-Petviashvili system[J].Journal of Mathematical Physics,2002,43(4):1956-1965.
[16]Zhai W,Chen D Y.N-soliton solutions of general nonlinear Schr¨odinger equation with derivative[J].Communications in Theoretical Physics,2008,49(5):1101-1104.
N-soliton solutions of combined AKNS-CLL equation
PAN Hong-fei,XIA Tie-cheng
(College of Sciences,Shanghai University,Shanghai 200444,China)
The bilinear form and N-soliton solutions are derived for a combined AKNSCLL equation using the Hirota approach.These solutions are novel in general.The one-soliton solutions of the combined AKNS-CLL equation,AKNS equation and CLL equation were drawn.Also,the combined AKNS-CLL equation is given a different characteristic from the classical AKNS and CLL equations.The bilinear form and N-soliton solutions of combined nonlinear Schr¨odinger equation are obtained by reduction.
combined AKNS-CLL equation;combined nonlinear Schr¨odinger equation;N-soliton solutions;Hirota approach
O 175.2
A
1007-2861(2015)06-0709-08
10.3969/j.issn.1007-2861.2014.04.002
2014-06-23
国家自然科学基金资助项目(11271008)
夏铁成(1960—),男,教授,博士生导师,研究方向为孤子与可积系统.E-mail:xiatc@shu.edu.cn

