基于中国剩余定理的门限RSA签名方案的改进
徐 甫 马静谨
基于中国剩余定理的门限RSA签名方案的改进
徐 甫*①②马静谨②
①(解放军信息工程大学 郑州 450002)②(北京市信息技术研究所 北京 100094)
针对基于中国剩余定理的门限RSA签名方案无法签署某些消息,以及部分签名合成阶段运算量大的问题,论文提出一种基于虚拟群成员的改进方法,使得改进后的方案能够签署所有消息,同时能够极大地减少部分签名合成阶段的运算量,当门限值为10时,可以将部分签名合成阶段的运算量减少为原来的1/6。对改进方案进行了详细的安全性和实用性分析。结果表明,改进方案在适应性选择消息攻击下是不可伪造的,且其运算效率较其他门限RSA签名方案更高。
门限签名;RSA签名方案;Asmuth-Bloom秘密共享;中国剩余定理
1 引言
随着分布式系统的广泛使用,以及对用户身份认证、密钥管理等手段的需求越来越强烈,门限签名方案逐渐成为了该领域的一个研究热点,并获得了广泛应用[4]。作为门限密码学的重要组成部分,门限签名由秘密共享与数字签名相结合而产生。在门限签名方案中,群体的签名密钥被所有个成员共同持有,使得群体中任意不少于个成员的子集可以代表群体对给定消息进行签名,而任意少于个成员的子集则不能产生有效的群签名。同时,门限签名不改变签名的验证方法,验证者只需要知道群体的唯一公开密钥,就可以简单而方便地验证群签名是否有效。
秘密共享方案(Secret Sharing Scheme, SSS)是门限签名的基础。已有的许多门限签名方案,包括门限RSA签名方案,ElGamal类门限签名方案[9,10]等,都使用基于拉格朗日插值方法的Shamir SSS[11]实现对签名私钥的共享。2007年,Kaya和Selçuk首次将基于中国剩余定理(Chinese Remainder Theorem, CRT)的Asmuth-Bloom SSS[12]引入了门限密码学,并利用该方案构造了门限RSA签名方案[13](以下简称“Kaya-Selçuk方案”)。
由于Asmuth-Bloom SSS自身的特性,将其应用于门限RSA签名方案时,在部分签名合成阶段,直接用各部分签名进行模乘运算只能生成一个不完整的群签名,需要经过矫正运算后,才能够得到正确的群签名。Kaya-Selçuk方案中,对于经过Hash函数处理的消息,矫正运算过程中需产生矫正因子,为元素在中的逆元。但是,由于不是素数,是交换环而不是域,在中的逆元未必存在。因此,Kaya-Selçuk方案并不是对所有消息都适用的。同时,矫正运算过程中,平均需要进行次模指数运算,以及一些辅助运算,增大了签名合成者的运算负担。
本文对Kaya-Selçuk方案进行了改进,通过引入一个虚拟群成员,在不需要矫正运算的情况下,保证了签名方案的正确性。在改进的Kaya-Selçuk方案中,不再需要对求逆,确保其对所有消息都适用。同时,由于不再需要矫正运算,减少了部分签名合成阶段的运算量,提高了签名的效率。
文章第2节简要介绍了背景及相关工作;第3节对Kaya-Selçuk方案进行改进;第4节对提出的改进方案进行正确性、安全性和实用性分析;第5节为结束语。
2 背景及相关工作
2.1门限签名方案及其安全性
验证:验证群签名是否正确。
定义2 适应性选择消息攻击:敌手可以在看到签名方案的公钥之后进行任意次的签名查询,而且可以根据已经观察到的签名选择新的消息进行签名查询。
2.2 Asmuth-Bloom SSS
Asmuth和Bloom于1983年以CRT为理论基础,提出了一种新的SSS[12]:为了在个成员中共享秘密,秘密分发者首先需执行如下步骤:
2.3 Kaya-Selçuk方案

(3)验证: 验证过程与标准RSA签名方案的验证过程相同,即验证是否成立,如成立则认为群签名有效。
3 改进的Kaya-Selçuk方案
改进的Kaya-Selçuk方案(以下简称“改进方案”)同样包括建立、签名和验证3个阶段。
(1)建立: 可信中心选择既为安全素数,又为Sophie Germain素数的两个大数和,计算及,那么和也为大素数。计算,,从中选择满足条件的和,分别作为公钥和私钥。用Kaya和Selçuk改进后的Asmuh-Bloom SSS对私钥进行共享,具体过程如下:
(b)合成部分签名:签名合成者按照步骤(a)的方法,为虚拟群成员计算部分签名,然后合成所有个部分签名,生成群签名
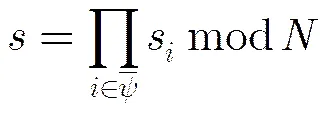
(3)验证:验证过程与Kaya-Selçuk方案的验证过程相同。
4 对改进方案的分析
4.1 正确性分析
引理1[14]设和是两个不同的素数,,则以及任意非负整数,有成立。
证明 根据CRT[14],有成立,因此,


4.2安全性分析
本节对改进方案进行安全性证明,证明过程中参考了Kaya-Selçuk方案安全性证明中的方法[13]。
定理2 如果标准RSA签名方案是适应性选择消息攻击下不可伪造的,则改进方案也是适应性选择消息攻击下不可伪造的。
证明 为了将改进方案的安全性归约为标准RSA签名方案的安全性,我们将构建模拟器SIM,其输入为改进方案的所有公开参数。其输出满足:从敌手E(具备适应性选择消息攻击能力)的角度看,与改进方案在运行过程中的输出信息是不可区分的。
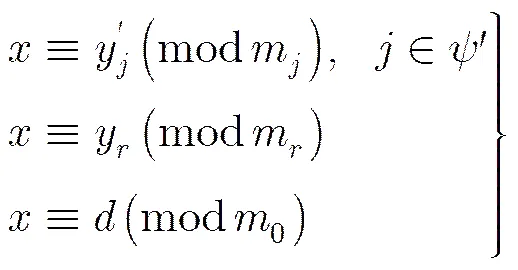

现在,假设敌手E能够伪造改进方案的群签名,那么,对于改进方案所依托的原始RSA签名方案,敌手在不知道密钥的情况下,可通过向原始RSA签名方案进行签名查询获得合法签名对,然后使用SIM模拟出改进方案的输出,并调用敌手E攻击改进方案的算法来产生消息的合法群签名,这样,敌手就成功伪造了在原始RSA签名方案中的签名。
4.3实用性分析
4.3.1对签名合成效率的影响分析 与Kaya-Selçuk方案相比,改进方案在运算量方面的变化主要在于签名合成阶段,合成者需要为虚拟群成员计算一个部分签名,而不再需要进行矫正运算。本节对两种方案中合成部分签名的运算量进行比较。

表1 (t,n)-Kaya-Selçuk方案中部分签名合成阶段需要的运算

表2 (t,n)-改进方案中部分签名合成阶段需要的运算
表1和表2中的运算包括模指数、模乘法、模逆等运算。其中,模指数运算中通常需要进行多次模平方运算和模乘法运算,以平方-乘算法为例[14],设的长度为bit,重量为,则计算(为中的任意值)共需要次模平方运算和次模乘法运算[14]。如果将模平方运算和模乘法运算的计算复杂性看作同一量级,并以取平均值来计算,计算的运算量大约相当于次模乘法运算。由于通常取1024 bit以上的大数,的长度仅比略小,而,其长度通常也较大,可能在512 bit以上。因此,与计算所需的运算量相比,表1中的模乘法运算的运算量可以忽略,模逆运算可使用减法和移位实现[16],其运算量同样可以忽略。同理,与计算所需的运算量相比,表1中的模乘法和模逆运算的运算量也可以忽略;与计算所需的运算量相比,表2中的模乘法和模逆运算的运算量也可以忽略。那么,-Kaya-Selçuk方案中部分签名合成的运算量约相当于计算和所需的运算量,约为次模乘法运算(由于较小,计算的运算量可忽略);而-改进方案中部分签名合成的运算量约相当计算所需的运算量,约为次模乘法运算。因此,改进方案的部分签名合成的运算量减少为原来的。当较大,比如时,改进方案的部分签名合成的运算量减少为原来的,极大地提高了部分签名合成的效率。
4.3.2与其他门限RSA签名方案的对比分析 由于门限签名的建立过程不会频繁进行,建立过程所需的运算量及通信量对方案的实用性影响不大,因此,我们主要针对签名阶段(包括部分签名产生和合成)和验证阶段对本文改进方案与现有的其他门限RSA方案进行对比。
除基于CRT的门限RSA门限签名方案之外,效率较高,具有代表性的门限RSA门限签名方案包括Shoup方案[5]和徐秋亮方案[6](以下简称“Xu方案”)。Kaya和Selçuk选择了Shoup方案作为签名效率的比较对象[13],但王贵林等人[17]提出了一种针对Shoup方案的改进方案(以下简称“Wang方案”),简化了其签名方程。因此,我们选择Wang方案和Xu方案作为本文改进方案的比较对象。表3列出了3种方案的部分签名产生、合成阶段和验证阶段的运算量(与上一节相同,仅考虑了模指数运算)。
由表3可知,本文改进方案在部分签名合成阶段运算量为其他两种方案的; 3种方案在部分签名产生阶段的运算量相同;验证阶段的运算量方面,改进方案与Shoup方案相同,为Xu方案的。总体来讲,与其他两种门限RSA签名方案相比,改进方案在运算效率方面具有较大的优势。
(3)签名合成者生成群签名后将其发送给签名请求者。
因此,改进方案的通信开销与其他两种方案基本相同。
5 结束语
本文针对Kaya和Selçuk提出的基于CRT的门限RSA签名方案的部分签名合成阶段需要进行中的求逆运算和复杂的矫正运算,导致该方案无法对某些消息进行签署,以及部分签名合成效率低下的问题,提出了一种改进方法,通过设置一个虚拟群成员,在部分签名合成阶段无需求逆运算和矫正运算的情况下,能够保证签名的正确性,使得改进后的方案能够签署所有消息。同时,由于不再需要矫正运算,使得部分签名合成的运算量大大减少,极大地提高了部分签名合成的效率,并合理选择了大素数,使得方案的安全性不受影响。
表3改进方案与其他门限RSA签名方案的运算量

签名方案部分签名产生阶段的模指数运算次数部分签名合成阶段的模指数运算次数验证阶段的模指数运算次数 Wang方案[17]11(忽略次数较小的模指数运算) Xu方案[6]12 本文改进方案111
[1] 马春光, 石岚, 周长利, 等. 属性基门限签名方案及其安全性研究[J]. 电子学报, 2013, 41(5): 1012-1015.
Ma Chun-guang, Shi Lan, Zhou Chang-li,.. Threshold attribute-based signature and its security[J]., 2013, 41(5): 1012-1015.
[2] 杨小东, 李春梅, 徐婷, 等. 无双线性对的基于身份的在线/离线门限签名方案[J]. 通信学报, 2013, 34(8): 185-190.
Yang Xiao-dong, Li Chun-mei, Xu Ting,.. ID-based on-line/off-line threshold signature scheme without bilinear pairing[J]., 2013, 34(8): 185-190.
[3] 崔涛, 刘培玉, 王珍. 前向安全的指定验证者(,)门限代理签名方案[J]. 小型微型计算机系统, 2014, 35(5): 1061-1064.
Cui Tao, Liu Pei-yu, and Wang Zhen. Forward secure (,) threshold proxy signature scheme with designated verifier[J]., 2014, 35(5): 1061-1064.
[4] 张文芳, 王小敏, 郭伟, 等. 基于椭圆曲线密码体制的高效虚拟企业跨域认证方案[J]. 电子学报, 2014, 42(6): 1095-1102.
Zhang Wen-fang, Wang Xiao-min, Guo Wei,.. An efficient inter-enterprise authentication scheme for VE based on the elliptic curve cryptosystem[J]., 2014, 42(6): 1095-1102.
[5] Shoup V. Practical threshold signatures[C]. Proceedings of EUROCRYPT 2000, Bruges, Belgium, 2000: 207-220.
[6] 徐秋亮. 改进门限RSA数字签名体制[J]. 计算机学报, 2000, 23(5): 449-453.
Xu Qiu-liang. A modified threshold RSA digital signature scheme[J]., 2000, 23(5): 449-453.
[7] 张文芳, 何大可, 王小敏, 等. 基于新型秘密共享方法的高效RSA门限签名方案[J]. 电子与信息学报, 2005, 27(11): 1745-1749.
Zhang Wen-fang, He Da-ke, Wang Xiao-min,.. A new RSA threshold group signature scheme based on modified Shamir’s secret sharing solution[J].&, 2005, 27(11): 1745-1749.
[8] Aboud S J, Yousef S, and Cole M. Undeniable threshold proxy signature scheme[C]. Proceedings of 5th International Conference on Computer Science and Information Technology, Amman, Jordan, 2013:150-153.
[9] Gennaro R, Jarecki S, Krawczyk H,.. Robust threshold DSS signatures[J]., 2001, 164(1): 54-84.
[10] Kim S, Kim J, Cheon J H,.. Threshold signature schemes for ElGamal variants[J].&, 2011, 33(4): 432-437.
[11] Shamir A. How to share a secret?[J]., 1979, 22(11): 612-613.
[12] Asmuth C and Bloom J. A modular approach to key safeguarding[J]., 1983, 29(2): 208-210.
[13] Kaya K and Selçuk A A. Threshold cryptography based on Asmuth-Bloom secret sharing[J]., 2007, 177(19): 4148-4160.
[14] 金晨辉, 郑浩然, 张少武, 等. 密码学[M]. 北京: 高等教育出版社, 2009: 244-367.
Jin Chen-hui, Zheng Hao-ran, Zhang Shao-wu,.. Cryptography[M]. Beijing: Higher Education Press, 2009: 244-367.
[15] Iftene S and Grindei M. Weighted threshold RSA based on the Chinese remainder theorem[C]. Proceedings of Ninth International Symposium on Symbolic and Numeric Algorithms for Scientific Computing, Timisoara, Romania, 2007: 175-181.
[16] 谭丽娟, 陈运. 模逆算法的分析、改进及测试[J]. 电子科技大学学报, 2004, 33(4): 383-386.
Tan Li-juan and Chen Yun. Analysis and improvement of modular inverse algorithm[J]., 2004, 33(4): 383-386.
[17] 王贵林, 卿斯汉, 王明生. Shoup门限RSA签名方案的改进[J]. 计算机研究与发展, 2002, 39(9): 1046-1050.
Wang Gui-lin, Qing Si-han, and Wang Ming-sheng. Improvement of Shoup’s threshold RSA signature scheme[J]., 2002, 39(9): 1046-1050.
Improvement of Threshold RSA Signature Scheme Based on Chinese Remainder Theorem
Xu Fu①②Ma Jing-jin②
①(,450002,)②(,100094,)
To slove the problems that Chinese Remainder Theorem (CRT) based threshold RSA signature scheme can not be used to sign some messages and the amount of computation in partial signatures combining phase is large, an improving method is proposed, in which a virtual group member is introduced, making the scheme can be used to sign all messages and significantly reducing the amount of computation in partial signatures combining phase, e.g. when the threshold value is 10, the amount of computation in partial signatures combining phase can be reduced to 1/6 of the original. The security and practicability of the improved scheme are analyzed. Results show that it is non-forgeable against an adaptive chosen message attack and more efficient than other threshold RSA signatures.
Threshold signature; RSA signature scheme; Asmuth-Bloom secret sharing; Chinese Remainder Theorem (CRT)
TP309
A
1009-5896(2015)10-2495-06
10.11999/JEIT150067
2015-01-12;改回日期:2015-05-28;
2015-07-17
徐甫 xuphou@163.com
国家科技重大专项(2012ZX03002003)
The National Science and Technology Major Project of China (2012ZX03002003)
徐 甫: 男,1983年生,博士生,研究方向为信息安全.
马静谨: 男,1981年生,工程师,研究方向为数据链安全.

