一种图像分割的快速不动点算法

李伟斌 易 贤 宋松和



一种图像分割的快速不动点算法

李伟斌*①②易 贤②宋松和③

①(中国空气动力研究与发展中心空气动力学国家重点实验室 绵阳 621000)②(中国空气动力研究与发展中心计算空气动力研究所 绵阳 621000)③(国防科学技术大学理学院 长沙 410073)

该文在去除背景便能获得目标的分割思想之上，提出了一个凸的无约束最小化问题。证明了问题提出过程中添加惩罚项的合理性，并通过实验验证了证明结果。在最小化求解方面，应用次微分和近似算子的相关理论，构造了求解的不动点算子，进而结合Opial-averaged定理，给出了求解所提凸优化问题的不动点算法，并理论推导出了收敛条件，证明了算法的收敛性。与经典文献方法的对比实验表明所提方法分割结果更精确。同时实验显示该文算法比梯度下降法和分裂Bregman方法更快速。另外，所提算法对初始曲线和噪声有较好的鲁棒性。

图像处理；图像分割；凸优化问题；不动点算法

1 引言

图像分割的任务是将一幅数字图像划分为多个互不相交的区域，每个区域具有某些视觉的共性，如颜色、亮度、纹理等。图像分割通常是用来确定物体位置或边界，已被广泛应用于天文、军事、医学等方面。近年来，图像分割方法层出不穷，且都取得了很好的分割效果。其中，变分方法凭借其理论的成熟性，更是成为了图像分割方法研究的热点。

变分图像分割模型的主要做法是从一定的分割思想入手，构造相应的能量泛函，进而应用优化技术对其最小化，由最小化过程得到的最优解便可给出最终的图像分割结果。大多数变分模型对应的能量函数是非凸构造的，这就导致分割结果过多地依赖于初始曲线的位置，有可能使得最终的演化曲线停留在离初始曲线较近、离目标较远的位置，即产生局部极小值的问题。文献[5]从Heaviside函数的近似入手，提出了一种凸的能量泛函，并应用梯度下降方法对其进行求解，实验表明这种算法能准确得到图像分割的全局解。针对凸能量泛函的最小化问题，各种优化方法层出不穷，应用最广的当属近年来出现的分裂Bregman方法[7]，该方法通过引入两个变量，用来避开长度项的直接计算，从而达到快速演化的目的。2011年，Micchelli等人[8]提出了基于不动点算法的图像去噪模型，并给出了算法的收敛性证明。

本文在文献[5]基础上，通过添加凸惩罚项，提出了一种改进的凸能量泛函，并证明了惩罚项加入的合理性。进而，结合次微分算子和近似算子相关理论，给出了最小化该凸能量泛函的不动点算法，证明了算法的收敛性。与经典模型和算法的对比实验表明本文方法能更快速准确得到分割结果，且对噪声和初始曲线具有较好的鲁棒性。

2 模型的提出

2.1 背景知识

背景去除模型[5]是基于区域的分割模型，它对含有模糊边界或噪声的图像具有更强鲁棒性。背景去除模型关注的是背景区域，旨在从图像中分离出背景区域。一般地，背景区域可以理解为图像中由灰度值相同(或相近)的像素点组成的最大区域。从该角度出发，背景去除模型的主要任务就是找出在灰度值相同(或相近)前提下，面积尽可能大的区域。

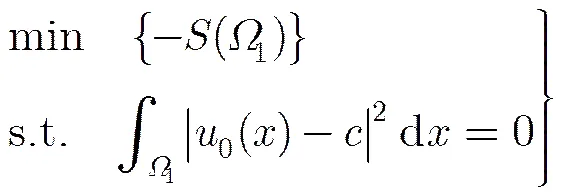
自然图像里各区域的灰度值很难达到同一化，因此式(1)中的约束条件很难满足，应用Lagrange乘子法弱化该约束条件。引入水平集函数[9]，将外部区域表征为，同时再应用Heaviside函数：

便可结合Lagrange乘子法由问题式(1)得到背景去除模型的能量泛函：

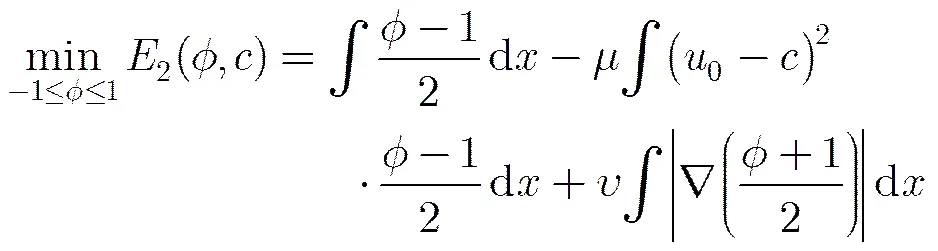
2.2 凸能量函数的提出

在文献[5]中，求解所提出的最小化问题式(3)使用的是较慢的梯度下降法。本文为了构造快速算法，在问题式(3)的基础上，为了去掉限制条件，引入凸的惩罚项，得到最小化问题：

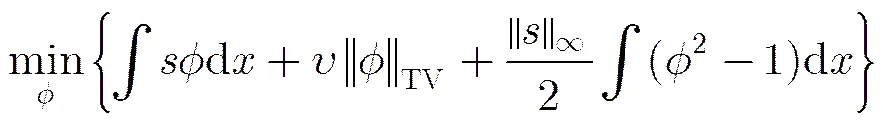
定理1 给定以下两个迭代序列：

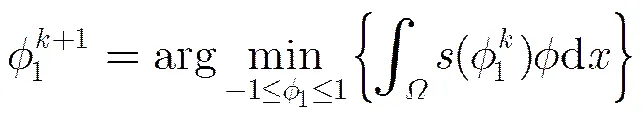
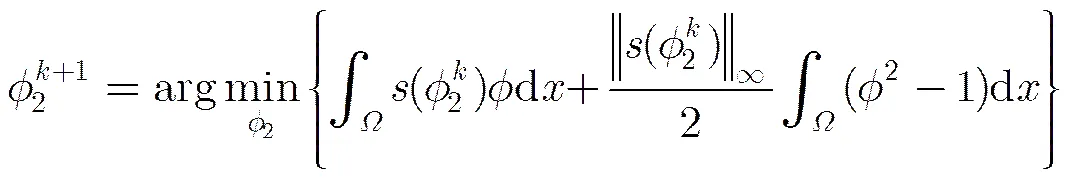
证明 证明主要分两部分：(1)迭代序列存在极限；(2)定理结论。

最后是五六条家乡的野鱼——麦穗鱼，不成风景，喧闹地追来追去。我也没在意，隔三差五，就有一条翻起白肚皮。两个月后，水安静了，也空了。

3 不动点算法

定义1[10]若函数是凸的，定义其在处的次微分算子为

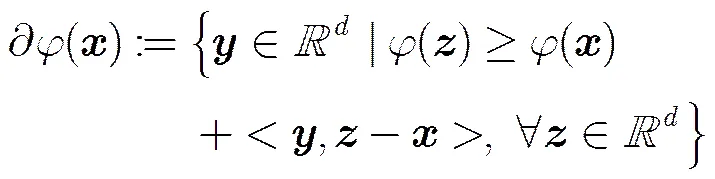
为

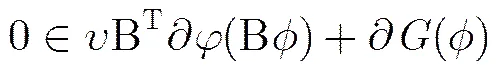
这里使用到了次微分的链式法则[11]：，其中算子对应着散度算子。因为是凸函数，且是可导的，因此，记，则式(7)可以转化为

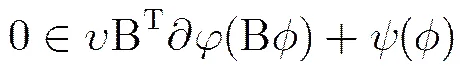
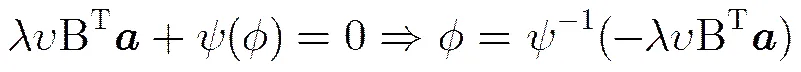
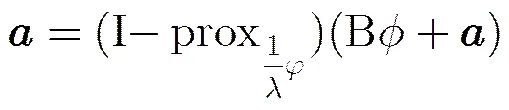
证明 结论可以分别通过式(7)至式(11)的正推和逆推过程得到。

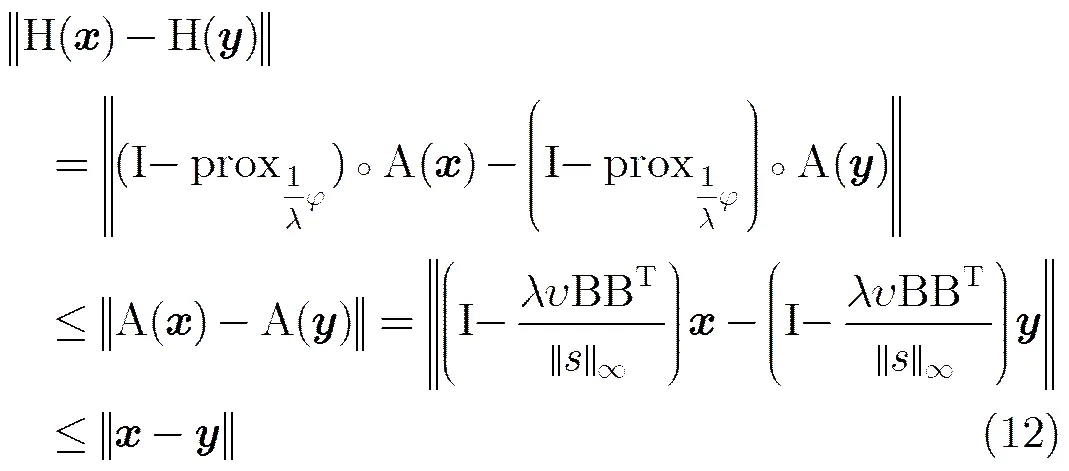
证毕

4 数值实验

这一节将本文方法与经典文献中的方法进行了对比实验，并将所提不动点算法与梯度下降法、分裂Bregman算法进行了比较。另外，还讨论了本文方法对初始曲线鲁棒性和噪声图像的适用性，同时验证了定理1的结论。为了便于参数设置，本文将测试图像的灰度值域由[0,255]线性变换为[0,1]，参数默认选取为,和，其他参数在每个实验中独立给出。

图1是对文献[13~15]与本文方法的分割结果对比。测试图像均取自Weizmann图像库[16]，其中第1列为该数据库中的人工分割结果，第2至4列分别为文献[13~15]的分割结果，第5列为本文方法分割结果。从图1(a)的标准可以看出，最理想的结果是将图像中两个宏观目标全部完整从背景中分割出去。从图中对比结果可知，文献[13~15]的方法并未能完整地给出正确结果，比如船桨、人形、牛额头和犄角等，这是由于这3种分割方法太过依赖图像的灰度信息，忽视了区域的完整性。而本文方法旨在从图像中分离背景区域，从而得到分割结果，因此给出了较准确的结果。从上至下，本文方法的参数为和。

图2是文献[5]与本文方法在特定步的分割结果对比，并且给出了相应的CPU时间。两种方法均采用同样的初始曲线，第1行和第2行分别是文献[5]和本文方法的分割结果。从第1列和第2列可以看出，当迭代进行10步之内时，文献[5]方法的演化曲线变化较小，而本文方法已给出较准确的分割结果；同时从第3列对比结果可以得出，本文方法在30步之前就已收敛，而文献[5]的分割结果中还有较多由噪声影响产生的小曲线。另外，从迭代步数所用的CPU时间可以看出，本文方法每一迭代步所用的时间较短。综上，本文方法相比于文献[5]可以在较短时间、较少迭代步数内取得正确分割结果，具有较高的分割效率。

为了验证不动点算法的快速准确性，本文将其与梯度下降方法和分裂Bregman方法进行对比试验。其中，梯度下降方法、分裂Bregman方法和不动点算法分别对式(2)，式(3)和式(4)进行最小化求解，而式(3)和式(4)均是基于式(2)提出的，因此它们的最小化问题是相同的。图3中的实验图像仍然选自Weizmann图像库，对比参数为迭代所用CPU时间和分割指标DSC(Dice Similarity Coefficient)，DSC是衡量分割准确度的测度，它的表达式为：

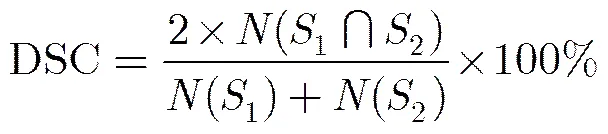
图1 自然图像分割结果对比

图2 文献[5](第1行)与本文方法(第2行)特定迭代步分割结果比较

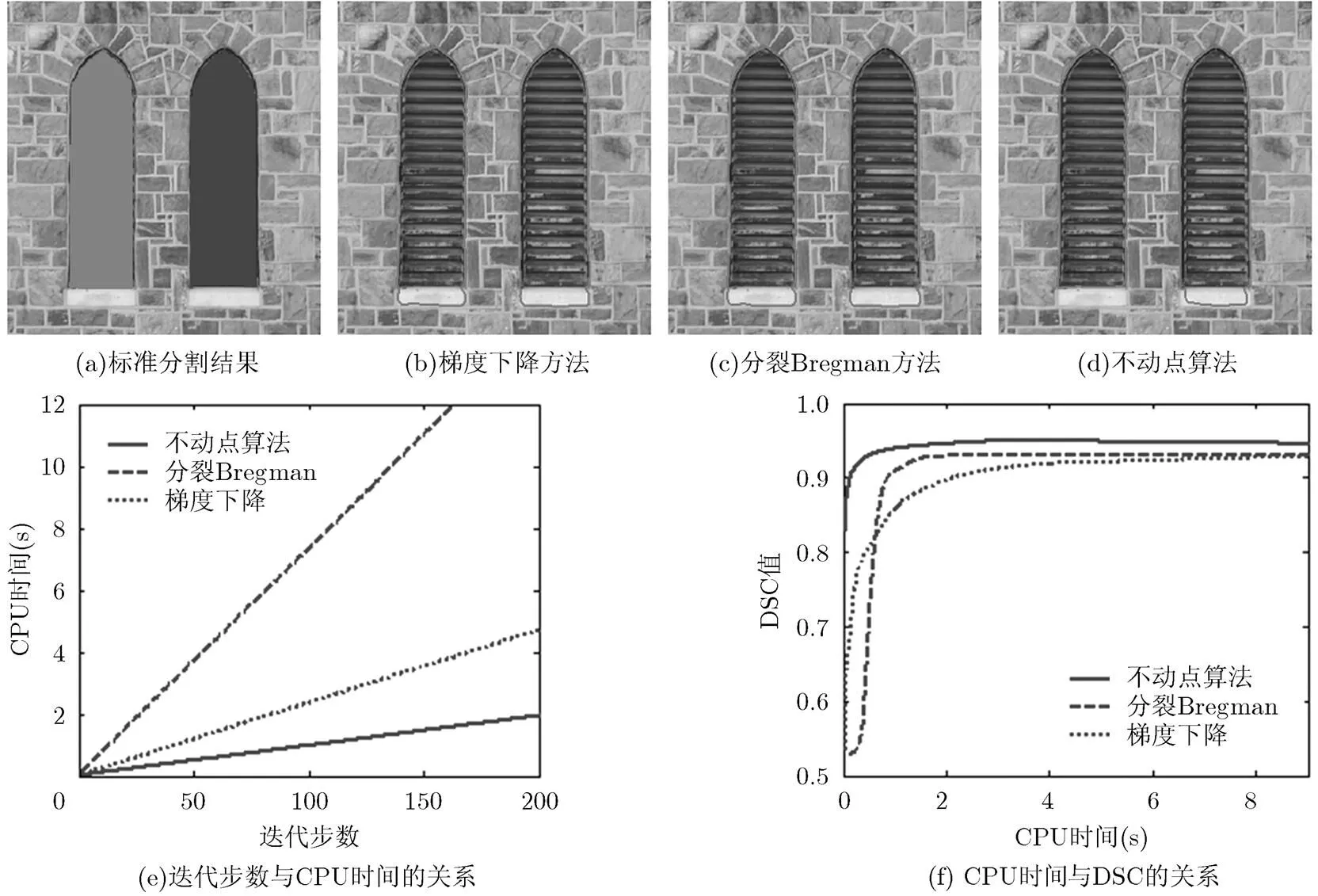
图3 梯度下降方法、分裂Bregman方法和不动点算法对比

为了构造本文的快速算法，在由提出能量泛函时，加入了凸的惩罚项，用于去掉的约束条件。定理1中已给出了情况下，加入该惩罚项的合理性。为了更进一步说明惩罚项加入的正确性，从实验角度对其进行验证。主要验证的是定理1的两个结论：对于任意的，有;。考虑图4(a)的初始情况，在图5(a)中给出了最大值和最小值关于迭代步数的曲线图，从图中可以看出，其始终满足的论断，即本文加入惩罚项的凸能量泛函隐含着的约束条件，这就使得问题的本质(式(3))没有发生变化。图5(b)中给出了迭代500步后的直方图，从直方图可以看出其大部分取值集中在0附近，也就是说近似满足的论断，没有全部为0的主要原因是定理给出的是长度项权重情况下的证明，而该实验中。

图4 不同初始曲线下的分割结果

图6中给出了本文算法对噪声图像的分割结果，其中第1行是添加了0均值Gauss噪声的图像，标准差分别为，第2行是对应的分割结果。从图6(a)可以看出，本文算法准确给出了两个物体的边缘，由于图像中不含噪声，曲线长度项系数选择较小，即为默认。从图6(b)到6(d)可以看出，针对噪声图像，本文算法仍然取得了较好的分割结果，但是随着噪声的增强，长度项系数变大，这使得算法不能较精确地给出小目标的边缘位置，如图6(d)左上角的分割结果。

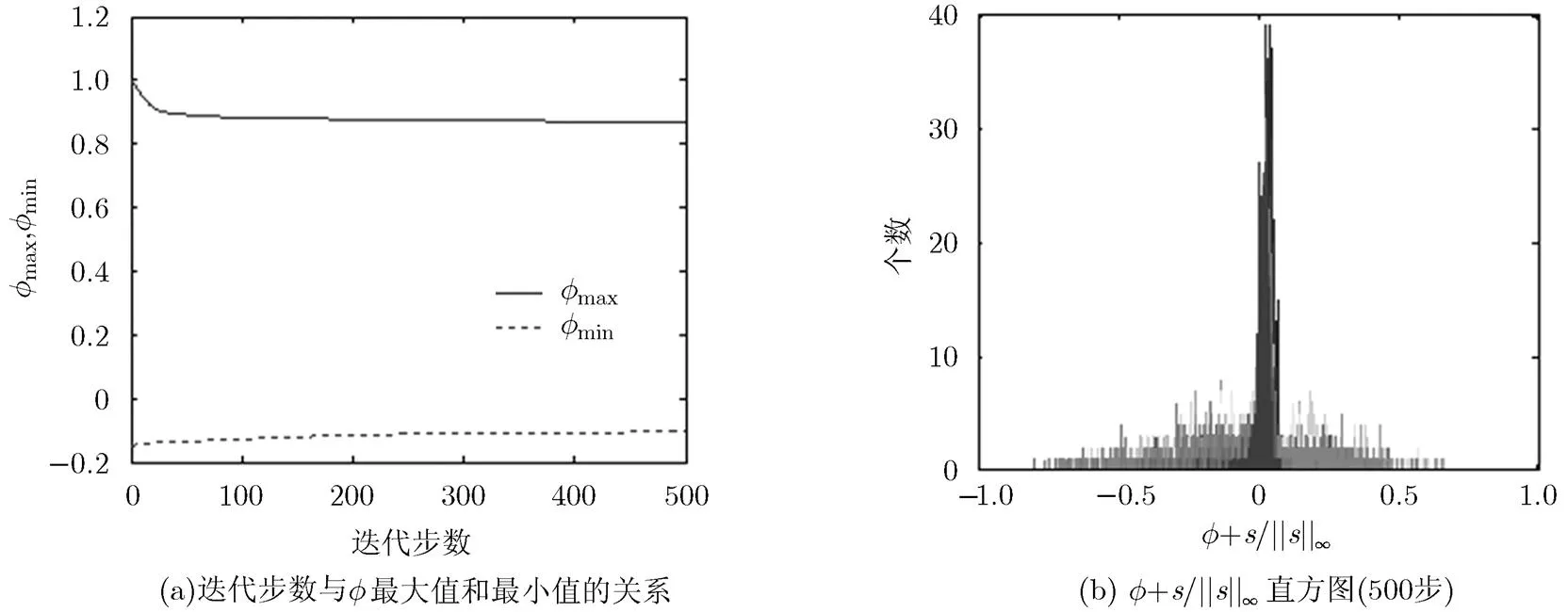
图5 图4(a)情况定量分析

图6 噪声图像分割结果

5 结束语

本文在前期的工作基础之上，通过添加凸的惩罚项，提出了一个不带约束条件的凸最小化问题，并证明了该问题与原问题的等价性，在实验部分，定量验证了等价性结论。在求解方面，本文应用次微分和近似算子的相关理论，给出了最小化所提问题的不动点算法，并证明了算法的收敛性。实验表明本文分割方法快速准确，对初始曲线选择无依赖，具有一定的抗噪性。

[1] Zhu W, Tai X, and Chan T. Image segmentation using Euler’s Elastica as the regularization[J]., 2013, 15(2): 414-438.

[2] Yuan J, Bae E, Tai X,.. A spatially continuous max-flow and min-cut framework for binary labeling problems[J]., 2014, 126(3): 559-587.

[3] 张泽均, 水鹏朗. 一种新的基于网格编码和区域合并的SAR图像快速分割算法[J]. 电子与信息学报, 2014, 36(4): 974-980.

Zhang Ze-jun and Shui Peng-lang. A new fast SAR image segmentation algorithm based on grid coding and region merging[J].&, 2014, 36(4): 974-980.

[4] 赵雪梅, 李玉, 赵泉华. 结合高斯回归模型和隐马尔可夫随机场的模糊聚类图像分割[J]. 电子与信息学报, 2014, 36(11): 2730-2736.

Zhao Xue-mei, Li Yu, and Zhao Quan-hua. Image segmentation by fuzzy clustering algorithm combining hidden Markov random field and Gaussian regression model[J].&, 2014, 36(11): 2730-2736.

[5] 李伟斌, 高二, 宋松和. 一种全局最小化的图像分割方法[J]. 电子与信息学报, 2013, 35(4): 791-796.

Li Wei-bin, Gao Er, and Song Song-he. A global minimization method for image segmentation[J].&, 2013, 35(4): 791-796.

[6] Li Wei-bin, Song Song-he, and Luo Feng. Fast image segmentation by convex minimisation and split Bregman method[J]., 2013, 49(17): 1073-1074.

[7] Goldstein T and Osher S. The split Bregman method for 1 regularized problems[J]., 2008, 2(2): 323-343.

[8] Micchelli C, Shen L, and Xu Y. Proximity algorithms for image models: denosing[J]., 2011, 27(4): 45009-45038.

[9] Osher S and Fedkiw R. Level Sset Methods and Dynamic Implicit Surfaces[M]. New York: Springer Verlag, 2002: 4-22.

[10] Bertsekas D. Nonlinear Programming[M]. Belmont: Athena Scientific, 2003: 209-210.

[11] Zălinescu C. Convex Analysis in General Vector Spaces[M]. River Edge: World Scientific, 2002: 79-88.

[12] Opial Z. Weak convergence of the sequence of successive approximations for nonexpansive mappings[J]., 1967, 73: 591-597.

[13] Chan T, Esedoglu S, and Nikolova M. Algorithms for finding global minimizers of image segmentation and denoising models[J]., 2006, 66(5): 1632-1648.

[14] Bresson X, Esedoglu S, Vandergheynst P,..Fast global minimization of the active contour/snake models[J]., 2007, 28(2): 151-167.

[15] Goldstein T, Bresson X, and Osher S. Geometric applications of the split Bregman method: segmentation and surface reconstruction[J]., 2010, 45(1-3): 272-293.

[16] Alpert S, Galun M, Basri R,. Image segmentation by probabilistic bottom-up aggregation and cue integration[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, 2007: 1-8.

Fast Fixed-point Algorithm for Image Segmentation

Li Wei-bin①②Yi Xian②Song Song-he③

①(,,621000,)②(,,621000,)③(,,410073,)

Based on the idea that objects in a given image can be segmented by ­­­­­removing the background part, an unconstrained convex minimization problem is proposed. The penalization term added in the construction procedure of the proposed problem is proven to be viable, which is demonstrated by the experiment. At the computational level, a fixed-point operator and the corresponding algorithm are proposed by applying the theory of subdifferential and proximity operators, and Opial-averaged theorem. And then the convergence proof of the algorithm is given. Comparisons with other classical models show that the proposed segmentation model is more accurate. And the experiments also demonstrate that the fixed-point algorithm is faster than the gradient descent method and the split Bregman method. Moreover, the algorithm is robust to the initial curve and noise.

Image processing; Image segmentation; Convex optimization; Fixed-point algorithm

TN911.73

A

1009-5896(2015)10-2390-07

10.11999/JEIT150112

2015-01-20；改回日期：2015-05-11；

2015-07-06

李伟斌 liweibin@nudt.edu.cn

国家自然科学基金(11172314)

The National Natural Science Foundation of China (11172314)

李伟斌： 男，1985年生，实习研究员，博士，主要研究方向为图像分割、变分方法和PDE方法.

易 贤： 男，1977年生，副研究员，主要研究方向为飞机结冰数值模拟和试验技术.

宋松和： 男，1965年生，教授，博士生导师，主要研究方向为PDE方法、图像处理和辛算法.