基于快速傅里叶变换的局部分块视觉跟踪算法

侯志强 张 浪 余旺盛 许婉君



基于快速傅里叶变换的局部分块视觉跟踪算法

侯志强 张 浪*余旺盛 许婉君

(空军工程大学信息与导航学院 西安 710077)

针对视觉跟踪中目标表观变化、局部遮挡、背景干扰等问题，该文提出一种基于快速傅里叶变换的局部分块视觉跟踪算法。通过建立目标分块核岭回归模型并构建循环结构矩阵进行分块穷搜索来提高跟踪精度，利用快速傅里叶变换将时域运算变换到频域运算提高跟踪效率。首先，在包含目标的初始跟踪区域建立目标分块核岭回归模型；然后，提出通过构造循环结构矩阵进行分块穷搜索，并构建目标分块在相邻帧位置关系模型；最后，利用位置关系模型精确估计目标位置并进行分块模型更新。实验结果表明，该文算法不仅对目标表观变化、局部遮挡以及背景干扰等问题的适应能力有所增强，而且跟踪实时性较好。

视觉跟踪；核岭回归模型；快速傅里叶变换；分块穷搜索；位置关系模型

1 引言

目标跟踪问题是当前计算机视觉领域中的一个热点问题，由于广泛应用于视频监控，图像压缩，3维重构等领域，其受到越来越多学者的关注。目标在运动过程中表观的不断变化、局部遮挡以及复杂背景的干扰常常导致跟踪失败。因此，构建合适的目标表示模型是决定跟踪成功与否的关键环节。

Mean Shift算法[4,5]利用目标颜色直方图特征构建目标模型，由于忽略了目标的空间结构信息，容易匹配到具有相似颜色直方图特征的背景中去。文献[6]采用修正的背景加权直方图对目标建模，能降低背景的干扰，但在复杂背景中跟踪效果不佳。多示例学习[7]利用目标正负样本构建目标的判别式模型，提高了算法对表观变化及复杂背景的适应性。基于循环结构的检测跟踪法[8,9]提出利用循环结构矩阵建立目标回归跟踪模型，但算法不能处理遮挡变化问题。近年来，基于局部分块模型的跟踪算法由于能很好地检测和处理遮挡问题而成为研究热点，局部分块可以分为规则分块和非规则分块。文献[10]提出的Fragments-based 分块方法是最具代表性的规则分块算法，但算法利用积分直方图进行穷搜索容易受到背景的干扰。文献[11-13]提高了分块的自适应能力，增强了算法对遮挡的处理能力。不规则分块以超像素[14,15]最具有代表性，由于超像素能很好地保持目标结构信息，跟踪鲁棒性较好。局部分块模型通过分块搜索提高了算法对目标变化的适应性。然而，现有局部分块跟踪算法对目标表观变化、局部遮挡及背景干扰等的适应能力有限。

针对以上问题，本文受分块跟踪启发提出一种基于快速傅里叶变换的局部分块穷搜索视觉跟踪算法，算法采用规则分块，保持了目标的空间结构信息，充分利用目标的表观信息并构建循环结构矩阵建立分块核岭回归模型，提高了算法对表观变化、背景干扰等情况的适应能力，通过求解目标分块在相邻帧位置关系模型有效剔除了分块误匹配，利用快速傅里叶变换将时域运算变换到频域运算有效提高了跟踪效率，实验结果验证了本文算法跟踪精确性和实时性。

2 基于快速傅里叶变换的核岭回归模型

核岭回归(Kernel Ridge Regression, KRR)是一种以结构风险最小化为学习准则，解决在原始样本空间中不能用线性方法求解的非线性问题的算法，该算法具有高泛化能力。

2.1核岭回归

线性回归是利用数理统计中的回归分析，可以用来确定两个或两个以上变量之间映射关系的一种统计分析方法，输出变量是输入变量的线性组合：

对于不适定问题，最小二乘法的解是病态的，构造式(2)所示代价函数：

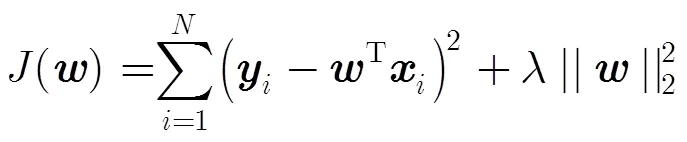
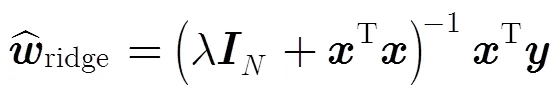
定义变量：

模型解可重写为

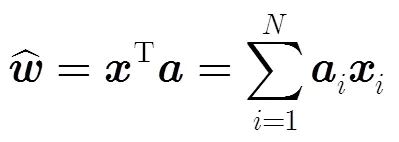
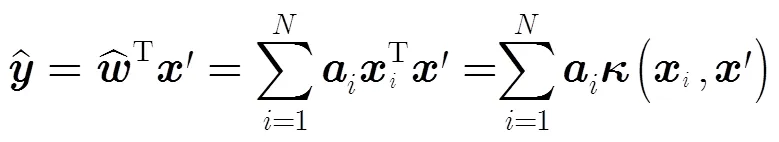
2.2 核空间的循环卷积

本节先介绍1维序列构造循环结构矩阵将时域运算转换到频域运算的原理，其结论可以推广至2维序列。假设有两个向量和，其卷积结果为一个+-1的向量：

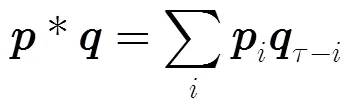
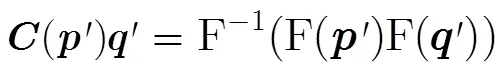
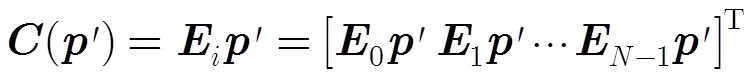
于是，式(5)可由时域变换到频域求解：

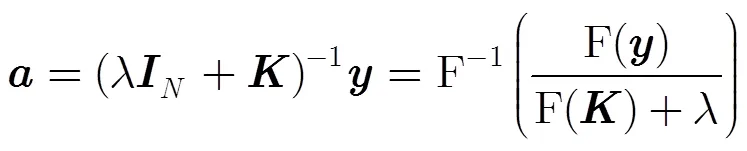
式(7)预测值为

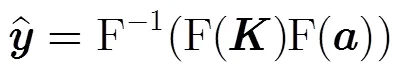
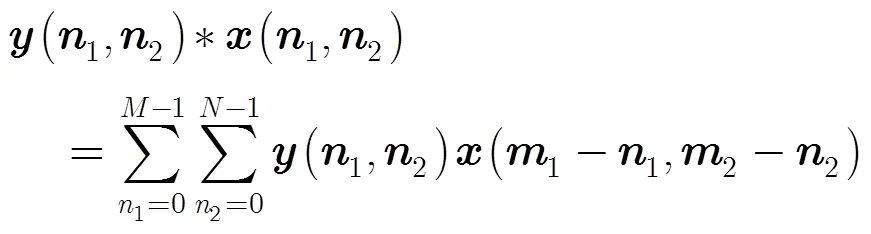
同理，有

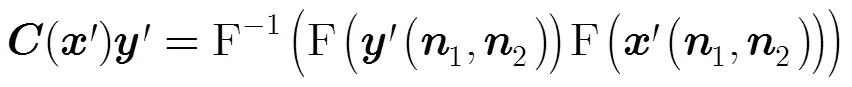
可以证明，式(5)式(7)可推广到2维矩阵[9]。2维矩阵循环沿水平和垂直两个方向进行，其示意图1如图所示。

2.3 循环穷搜索

图1 构造循环结构示意图

3 分块模型的构建

当前分块方式可以分为规则分块和非规则分块，文献[10]给出了一种简单的规则分块方式，本文采用的规则分块，并对每个分块分别建立核岭回归模型来对目标进行描述表示。图2和图3分别为文献[10]和本文算法的分块示意图。

4 位置关系模型及模型更新

通过构建的目标分块模型进行分块穷搜索，可以得到目标分块在当前帧的位置，已知目标分块在上一帧位置的情况下，通过构建目标分块在相邻帧间位置点集的位置关系模型即可精确估计出目标位置。本文为方便表示，以六边形顶点表示目标各分块位置，六边形中心表示目标中心位置，示意图如图4示。其中，和分别表示第帧图像和第帧图像的对应分块位置点集，为和分别为对应目标中心位置，为分块数。

本文选取目标分块对应位置计算位置平移，相邻帧位置关系模型表示为

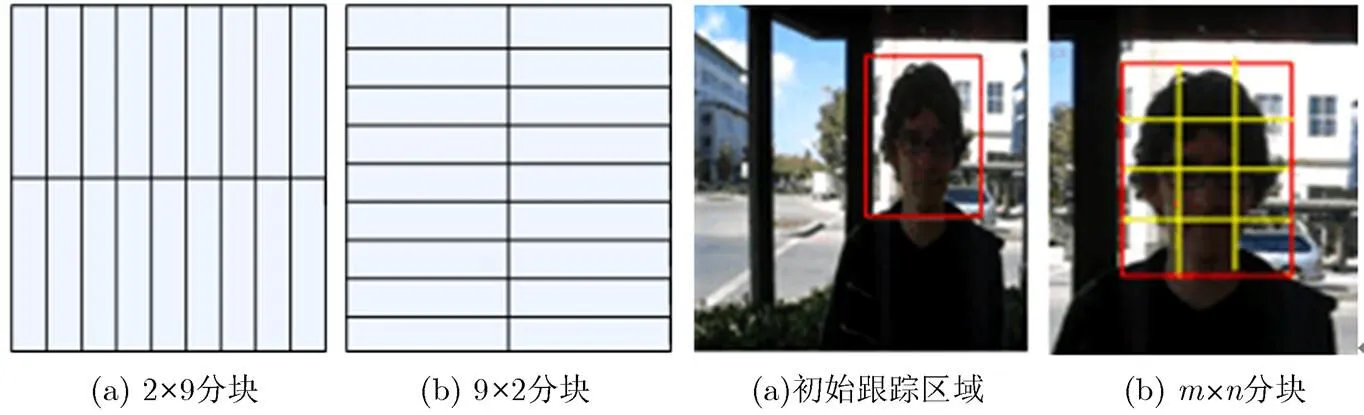
图2 文献[10]分块方法        图3 本文算法目标分块示意图

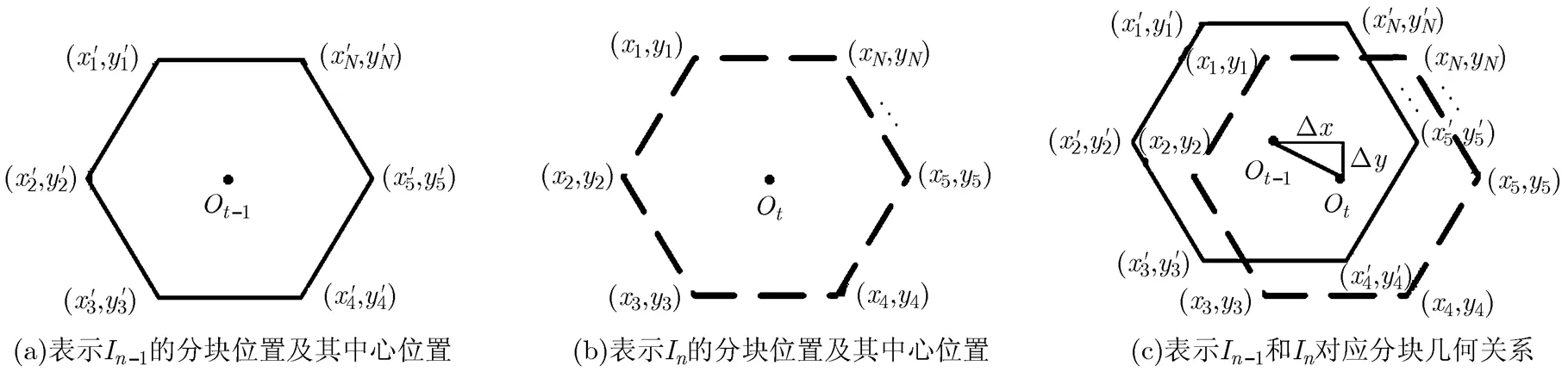
图4 目标分块在相邻帧位置关系模型

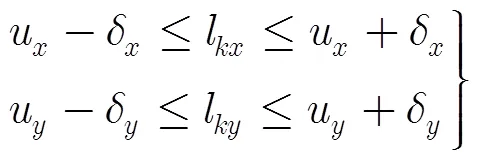
遍历所有分块的的位移量，保留满足上述条件的分块位移量并由此可以得到目标在当前帧的位置。同时，记录所有分块相邻帧匹配关系，若不满足约束条件，则可能发生目标表观较大变化、局部遮挡或背景干扰等情况，因而不进行模型更新，否则，设置模型更新因子对分块模型进行融合更新：

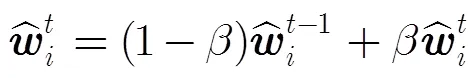
5 算法流程

基于FFT的局部分块穷搜索算法如表1所示。

表1基于FFT的局部分块穷搜索算法

输入：图像，初始目标位置，分块数目。输出：当前帧目标位置及分块中心位置点集。如果k=1，则(1)根据输入的初始条件对目标进行分块，获得目标分块位置点集；(2)对目标各分块构造循环结构矩阵，建立回归模型，得到目标的分块模型。如果k>1，则(1)根据输入条件确定目标分块的搜索区域；(2)利用已经构建的分块模型，对各分块进行模型学习，确定各分块位置；(3)计算目标分块的位置关系模型，精确估计出目标位置，并进行模型更新。

本文跟踪算法流程图如图5所示。

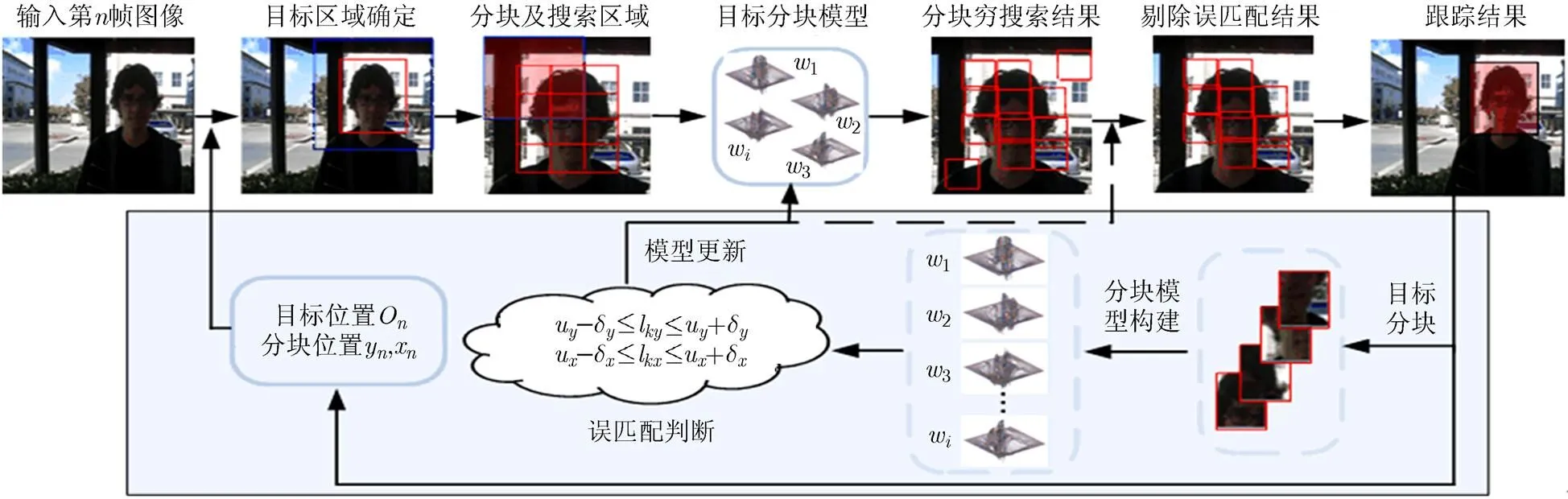
图5 本文算法跟踪过程示意图

6 实验结果与分析

为验证本文跟踪算法的有效性，进行了大量实验仿真。实验中使用的分块数目，每个分块的局部穷搜索范围为该分块大小的倍，核岭回归模型正则化参数，高斯核方差，模型更新因子，模型更新因子取值区间是经过大量实验得到，在不同视频需人为设定最佳值。

为了充分说明本文算法在处理目标表观变化、背景干扰、局部遮挡及光照变化等方面的优势，本文有针对性地选取了9组具有挑战性的测试视频和4种对比算法：9组视频及目标真实位置均来自文献[3], 4种对比算法分别是：Frag[10], CBWH[6], MIL[7]和SPT[14]。为保证对比实验的公平性，Frag和MIL算法跟踪结果直接使用文献[3]公布的公开结果，其余算法均进行了多次实验并取最优结果。所有实验都在联想CPU-E5300 @2.60 GHz, 3.25 GB内存的台式机进行，算法通过MATLAB2009a实现。9组视频序列，4种算法的跟踪对比结果如图6所示。

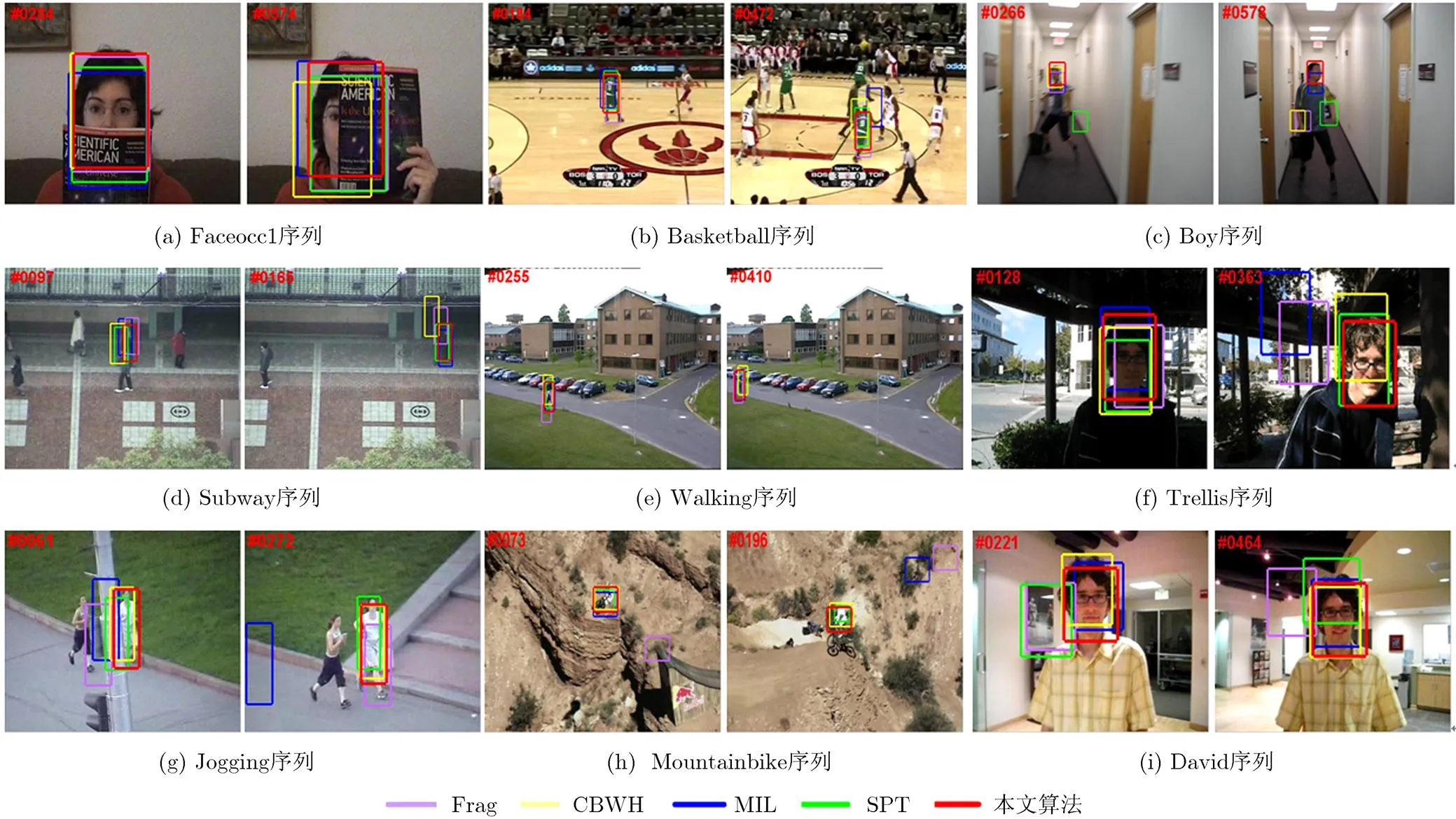
图6 跟踪算法性能的定性比较

6.1定性对比

(1)局部遮挡目标跟踪 局部遮挡使得跟踪算法不能获得足够的目标信息而导致跟踪偏差或丢失；本文选取了Faceocc1序列、Subway序列及Jogging序列来验证本文算法对遮挡的适应能力。MIL 算法和CBWH 算法对局部遮挡的适应能力较差，跟踪误差较大；Frag算法、SPT算法以及本文算法都采用的了分块模型来处理遮挡问题，但当目标被严重遮挡后，Frag算法和SPT算法均出现丢失或明显偏差情况，而本文算法由于利用目标的表观模型进行局部穷搜索，当目标再次出现时仍能成功跟踪目标，如Jogging序列第61帧所示。

(2)背景干扰目标跟踪 背景干扰是目标跟踪中最常见的跟踪问题，由于背景中具有与目标特征相似的背景物而导致跟踪丢失或偏差；本文选取Basketball序列、Walking序列和Mountainbike序列来验证本文算法与其他几种对比算法适应背景干扰的能力；当出现复杂背景干扰时，MIL算法丢失目标，Frag算法和CBWH算法都出现一定程度的跟踪偏差；如Basketball序列472帧所示；SPT算法和本文算法均能较好适应背景干扰问题，但SPT算法会由于跟踪过程模型误差的累积，最终出现一定程度的跟踪误差，本文算法具有更好的跟踪目标。

(3)快速运动目标跟踪 快速运动常常导致图像模糊，使得跟踪算法难以获得目标的表观信息而导致跟踪丢失。如图Boy序列266帧所示，当目标快速运动出现图像模糊时， Frag算法、CBWH算法和SPT算法均出现目标丢失情况；MIL算法和本文算法均能成功跟踪目标，但本文算法充分利用目标表观信息建模,能更好适应目标表观变化。

(4)光照变化目标跟踪 光照变化常常导致目标的颜色信息发生明显变化，因而容易出现跟踪丢失或偏差；本文选取Trellis序列和David序列来对比本文算法和其他算法对光照变化的适应能力。当光照发生明显的非线性变化时，Frag算法和MIL算法丢失跟踪目标，CBWH亦存在较大跟踪偏差，如Trellis序列363帧所示，当目标从较暗环 境移动到较亮环境时，SPT算法跟踪丢失，如David序列221帧所示，而本文算法能较好成功跟踪目标。

6.2定量分析

为衡量跟踪算法的跟踪性能，本文采用平均每帧运行时间(单位：s)、中心位置误差(单位：像素)和跟踪成功率来对本文算法和对比算法进行对比分析。平均每帧运行时间衡量跟踪效率，值越小跟踪效率越高。中心位置误差和跟踪成功率衡量跟踪精度。误差值越小跟踪精度越好，成功率值越大跟踪精度亦越好。

6.2.1跟踪效率 表2所示为本文算法与对比算法平均每帧运行时间比较结果，其中粗体表示最优算法，粗斜体表示次优算法(下同)。可以看出，由于构造循环结构矩阵，利用快速傅里叶变换将时域运算转换到频域运算有效地提高了跟踪效率，本文算法在所有测试序列中均具有最好的跟踪实时性。

表2平均每帧运行时间(s)

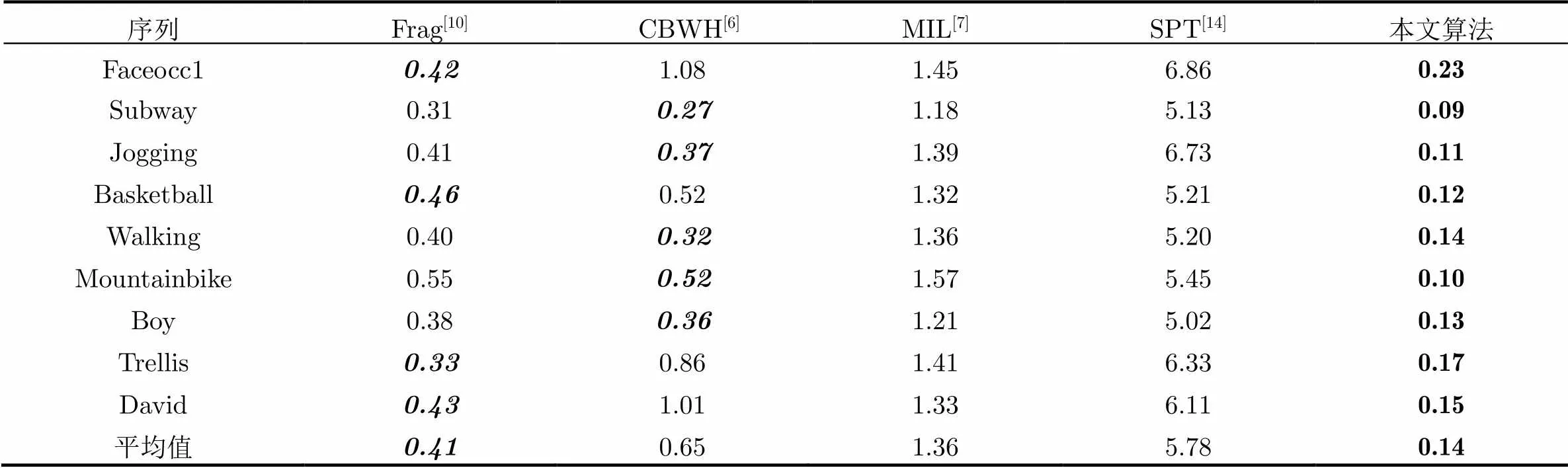
序列Frag[10]CBWH[6]MIL[7]SPT[14]本文算法 Faceocc10.421.081.456.860.23 Subway0.310.271.185.130.09 Jogging0.410.371.396.730.11 Basketball0.460.521.325.210.12 Walking0.400.321.365.200.14 Mountainbike0.550.521.575.450.10 Boy0.380.361.215.020.13 Trellis0.330.861.416.330.17 David0.431.011.336.110.15 平均值0.410.651.365.780.14

6.2.2跟踪精度

(a)中心位置误差 图7所示为本文算法与对比算法的中心位置误差对比曲线图，可以看出，Frag算法在Faceocc1序列具有较小的跟踪误差；CBWH在Trellis序列和Jogging等序列中跟踪误差相对较小且稳定；MIL算法在Walking序列、Boy序列、Subway序列和David序列的跟踪结果较为准确，SPT算法除在Boy序列和David序列跟踪效果较差外，其余序列都取得了较好的跟踪效果；本文算法在所有序列中都具有较小的中心位置误差。

表3所示为目标中心位置平均误差值比较结果，其中粗体表示最优算法，粗斜体表示次优算法。可以看出，Frag 算法在Faceocc1序列的具有最优跟踪结果，MIL算法在Boy序列和Walking序列取得次优跟踪结果，SPT算法在Basketball序列取得最优跟踪效果，在Subway序列和Trellis序列取得次优跟踪结果，本文算法在9组测试序列中取得7组最优结果和2组次优结果，在平均跟踪误差上取得最优跟踪结果。

表3目标中心位置平均误差比较(像素)

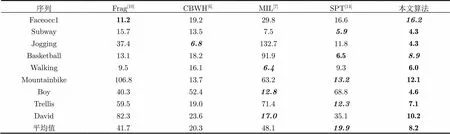
序列Frag[10]CBWH[6]MIL[7]SPT[14]本文算法 Faceocc111.219.229.816.616.2 Subway15.713.57.55.94.3 Jogging37.46.8132.711.84.3 Basketball13.118.291.96.58.9 Walking9.516.16.49.36.0 Mountainbike106.813.763.213.212.1 Boy40.352.412.868.84.6 Trellis59.519.071.412.37.1 David82.323.617.035.110.2 平均值41.720.348.119.98.2

(b)跟踪成功率 表4所示为跟踪成功率比较结果。Frag 算法在Faceocc1序列取得很好的跟踪结果，CBWH 在Jogging 序列取得不错的跟踪结果，MIL算法SPT 算法分别在几组序列中取得较好跟踪结果，其中SPT算法在Basketball序列和Faceocc1序列取得最优跟踪结果，在Trellis序列和Mountainbike序列具有次优跟踪结果，本文算法在9组测试序列中取得8组最优结果和1组次优结果，在平均跟踪成功率上取得最优结果。

6.3 分块方式及与 Frag算法和SPT算法的对比分析

分块方式分为规则分块和非规则分块，由于需要构造循环结构矩阵，以便利用快速傅里叶变换将时域运算变换到频域运算，因此目标状态需采用矩形框描述，故本文算法分块方式采用与Frag算法类似的分块方式，相比超像素，超像素分块方法通过聚类能更好地保持目标局部特征，其缺点是聚类时间长，影响跟踪的实时性。本文分块方式虽未能很好保持目标局部特征，但是通过构造循环结构矩阵建立目标分块核岭回归模型，本文算法取得了更好的跟踪精度和跟踪效率。

表4跟踪成功率比较

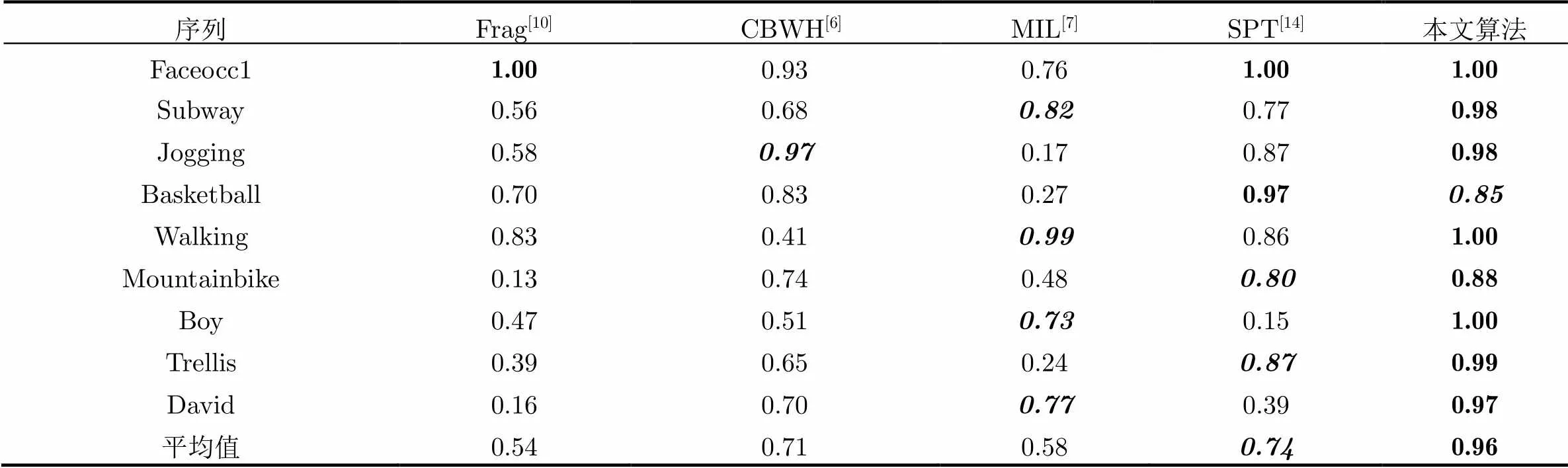
序列Frag[10]CBWH[6]MIL[7]SPT[14]本文算法 Faceocc11.000.930.761.001.00 Subway0.560.680.820.770.98 Jogging0.580.970.170.870.98 Basketball0.700.830.270.970.85 Walking0.830.410.990.861.00 Mountainbike0.130.740.480.800.88 Boy0.470.510.730.151.00 Trellis0.390.650.240.870.99 David0.160.700.770.390.97 平均值0.540.710.580.740.96

实验发现，本文算法相比Frag算法和SPT算法在跟踪效率和跟踪精度上具有一定优势；Frag算法采用规则分块来对目标进行描述，保持了目标的空间结构信息，能较好处理局部遮挡问题，但是对分块进行搜索时，该算法使用积分直方图进行穷搜索容易受到复杂背景的干扰而出现跟踪丢失情况，如图6(f)所示；SPT 算法通过聚类对目标进行非规则分块，有效利用了目标的中层视觉线索，能较好处理局部遮挡和表观变化等问题，但是算法需要建立在上一帧跟踪结果具有一定精度且运动空间连续的基础上，当目标快速运动导致图像模糊或跳跃运动时，算法因不能有效分割目标而跟踪失败，如图6(c)所示，同时，该算法由于需要对目标进行聚类分析，实时性较差，如表2所示。

本文算法采用规则分块，保持了目标的空间结构信息，并充分利用目标的表观信息建立分块核岭回归模型，通过构造循环结构矩阵进行分块穷搜索并构建目标分块在相邻帧位置关系模型能准确定位目标位置，提高了算法对目标表观变化、背景干扰及光照变化的适应能力，将时域运算转换到频域运算能有效提高跟踪效率，实验结果验证了本文算法跟踪精确性和实时性。

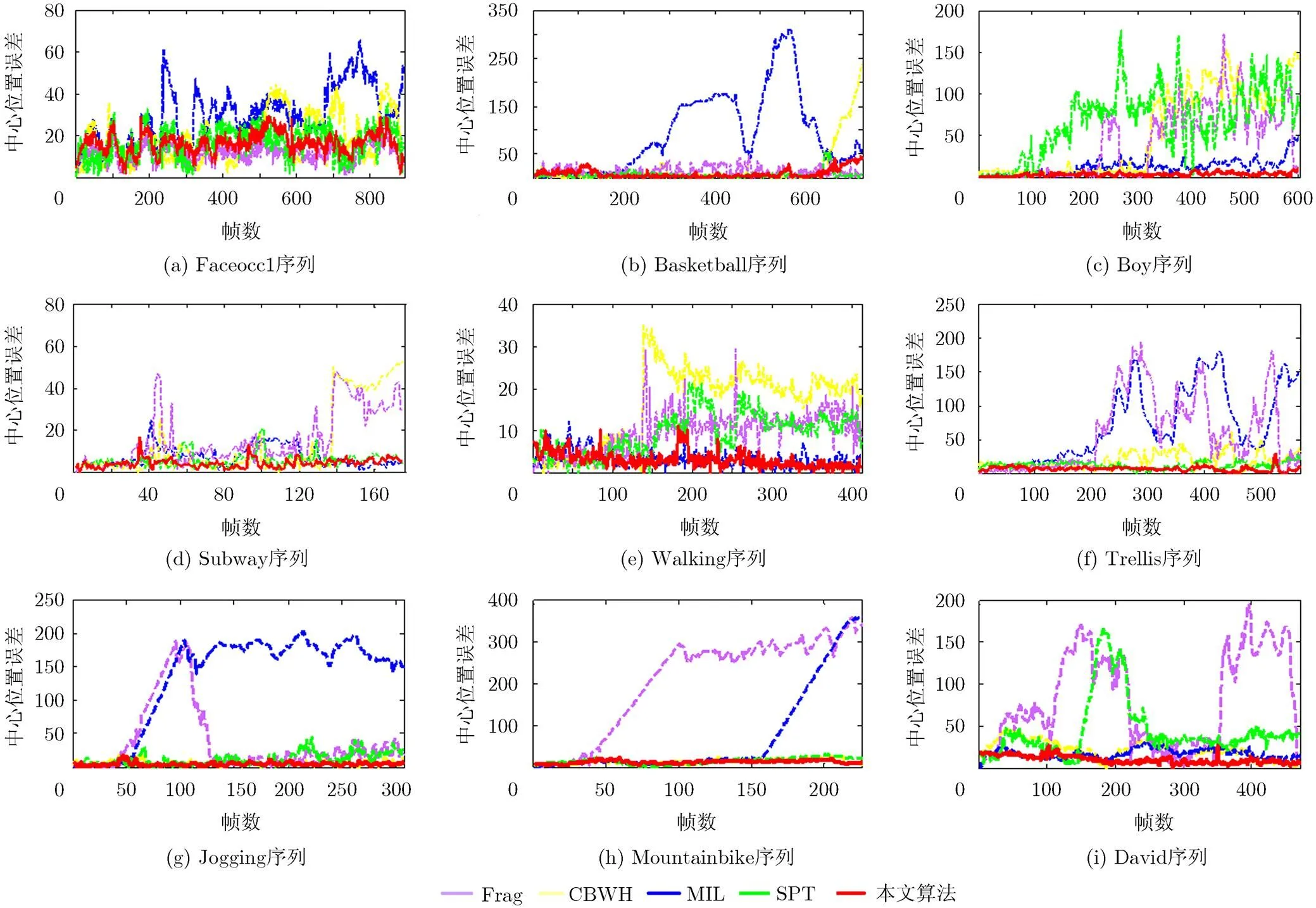
图7 中心位置误差比较(单位：像素)

7 结束语

在传统分块目标模型的基础上，本文提出了一种基于快速傅里叶变换的局部分块视觉跟踪算法。算法建立目标的分块核岭回归模型，不仅保持了目标的空间结构信息，而且充分利用了目标的表观信息，能有效处理表观变化、局部遮挡、背景干扰等问题，同时通过构建循环结构矩阵进行分块穷搜索并建立目标位置关系模型，提高了跟踪精度和跟踪效率。实验结果表明，本文算法能较好处理目标表观变化、遮挡、背景干扰等问题，取得较好的跟踪精度和跟踪效率。然而，本文算法未考虑目标的尺度和旋转变化问题，下一步工作将考虑算法对目标尺度和旋转变化的自适应问题，以进一步提高跟踪算法的鲁棒性。

[1] Yang H X, Shao L, Zheng F,.. Recent advances and trends in visual tracking: a review[J]., 2011, 74(18): 3823-3831.

[2] Smeulders A W, Chu D M, Cucchiara R,.. Visual tracking :an experimental survey[J]., 2014, 36(7): 1442-1468.

[3] Wu Y, Lim J, and Yang M H. Online object tracking: a benchmark[C]. Proceedings of the Computer Vision and Pattern Recognition, Portland, United States, 2013: 2411-2418.

[4] Comaniciu D and Ramesh V. Kernel-based object tracking[J]., 2003, 25(5): 564-577.

[5] Collins R T. Mean-Shift blob tracking through scale space[C]. IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Madison, United States,2003: 234-240.

[6] Ning J F, Zhang L,.. Robust mean shift tracking with corrected background-weighted histogram[J].,2012, 6(1): 62-69.

[7] Babenko B, Yang M H, and Belongie S. Robust object tracking with online multiple instance learning[J]., 2011, 33(8): 1619-1632.

[8] Henriques J F, Caseiro R, Martins P,.. Exploiting the circulant structure of tracking-by-detection with kernels[C]. Proceedings of European Conference on Computer Vision (ECCV),Florence, Italy, 2012: 702-715.

[9] Henriques J F,Caseiro R, Martins P,.. High-speed tracking with kernelized correlation filters[J]., 2015, 37(3): 583-596.

[10] Adam A, Rivlin E, and Shimshoni I. Robust fragments-based tracking using the integral histogram[C]. Proceedings of the Computer Vision and Pattern Recognition, New York, United States, 2006: 798-805.

[11] 董文会, 常发亮, 李天平. 融合颜色直方图及SIFT特征的自适应分块目标跟踪方法[J]. 电子与信息学报, 2013, 35(4): 770-776.

Dong W H, Chang F L, and Li T P. Adaptive fragments- based target tracking method fusing color histogram and SIFT features[J].&, 2013, 35(4): 770-776.

[12] Nejhum S, Ho J, and Yang M H. Online visual tracking with histograms and articulating blocks[J]., 2010, 114(8): 901-914.

[13] Yang F, Lu H C, and Chen Y W. Bag of feature tracking[C]. Proceedings of the International Conference on Pattern Recognition, Istanbul, Turkey, 2010: 153-156.

[14] Wang S, Lu H C, Yang F,.. Superpixel tracking[C]. Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 2011: 1323-1330.

[15] Yang F, Lu H C, and Yang M H. Robust superpixel tracking[J]., 2014, 23(4): 1639-1651.

Local Patch Tracking Algorithm Based on Fast Fourier Transform

Hou Zhi-qiang Zhang Lang Yu Wang-sheng Xu Wan-jun

(,,710077,)

In order to solve the problems of appearance change, local occlusion and background distraction in the visual tracking, a local patch tracking algorithm based on Fast Fourier Transform(FFT)is proposed. The tracking precision can be improved by establishing object’s patch kernel ridge regression model and using patch exhaustive search based on circular structure matrix, and the efficiency can be improved by transforming time domains operation into frequency domains based on FFT. Firstly, patch kernel ridge regression model is constructed according to the initialized tracking area. Secondly, a patch exhaustive search method based on circular structure matrix is proposed, then the position model is constructed in adjoining frame. Finally, the position of the object is estimated accurately using the position model and the local patch model is updated.Experimental results indicate that the proposed algorithm not only can obtain a distinct improvement in coping with appearance change, local occlusion and background distraction, but also have high tracking efficiency.

Visual tracking; Kernel ridge regression model;Fast Fourier Transform (FFT); Patch exhaustive search; Position model

TP391.4

A

1009-5896(2015)10-2397-08

10.11999/JEIT150183

2015-02-02；改回日期：2015-06-03；

2015-07-06

张浪 zhanglangwy@126.com

国家自然科学基金(61175029, 61473309)和陕西省自然科学基金(2011JM8015)

The National Natural Science Foundation of China (61175029, 61473309); The Natural Science Foundation of Shaanxi Province (2011JM8015)

侯志强： 男，1973年生，教授，主要研究方向为图像处理、计算机视觉和信息融合.

张 浪： 男，1990年生，硕士生，研究方向为视觉跟踪.

余旺盛： 男，1985年生，讲师，主要研究方向为图像分割、视觉跟踪.

许婉君： 女，1990年生，硕士生，研究方向为视觉跟踪.