一种基于误差距离加权与跳段算法选择的遗传优化DV-Hop定位算法

程 超 钱志鸿 付彩欣 刘晓慧



一种基于误差距离加权与跳段算法选择的遗传优化DV-Hop定位算法

程 超 钱志鸿*付彩欣 刘晓慧

(吉林大学通信工程学院 长春 130012)

针对DV-Hop (Distance Vector-Hop) 定位算法存在较大定位误差的问题，该文提出了一种基于误差距离加权与跳段算法选择的遗传优化DV-Hop定位算法，即WSGDV-Hop定位算法。改进算法用基于误差与距离的权值处理锚节点的平均每跳距离；根据判断的位置关系选择适合的跳段距离计算方法；用改进的遗传算法优化未知节点坐标。仿真结果表明，WSGDV-Hop定位算法的性能明显优于DV-Hop定位算法，减小了节点定位误差、提高了算法定位精度。

无线传感器网络；遗传算法；归一化加权；DV-Hop(Distance Vector-Hop) 定位算法；判断选择

1 引言

随着无线通信技术的不断发展与壮大，作为物联网(Internet of Things, IoT)底层重要技术之一的无线传感器网络(Wireless Sensor Network, WSN)已经成为了研究热点[1]。WSN可以使IoT在任意时间、地点获取任何想要得到的监测信息。而在WSN中监测信息的采集节点的位置是至关重要的，没有位置信息的监测信息毫无意义，只有已知位置的监测信息才有理论研究意义和实际应用价值，因此在WSN中能够确定监测信息采集位置的定位技术成为了WSN研究的关键问题之一，也是目前国内外的研究重点。

根据实际计算传感器节点间的距离或角度，把无线传感器网络定位算法分为基于距离(range- based)的和距离无关(range-free)的两种定位算法。其中，基于距离定位算法是在定位过程中通过使用外界设备来计算节点间距离或角度，再利用计算得到的距离角度信息进行未知节点位置定位的一种定位算法，包括：基于RSSI(Received Signal Strength Indicator)的定位[2]，基于TOA(Time Of Arrival)的定位[3]，基于AOA(Angle Of Arrival)的定位[4]和基于TDOA(Time Difference Of Arrival)的定位[5]。距离无关定位算法是在定位过程中无需使用外界设备计算节点间距离或角度，只需要根据网络拓扑关系和锚节点的位置就可以进行未知节点位置定位的一种定位算法，包括：APIT (Approximate Point-In- triangulation Test)算法、DV-Hop(Distance Vector- Hop)定位算法[6,7]、质心算法[8]以及Amorphous算法[9,10]等。基于距离定位算法需要使用外界设备才能对未知节点的位置进行定位，网络能耗大、成本高，但是该算法的定位精度高；而距离无关定位算法无需使用外界设备就可以对未知节点的位置进行定位，网络能耗小、成本低，但是该算法的定位精度低，虽然低但该低定位精度依然可以满足实际应用，所以距离无关定位算法成为了WSN定位算法中的重点研究算法。

在WSN的众多距离无关定位算法中，性能较优的DV-Hop定位算法由于具备了距离无关定位算法的全部优点而得到了国内外研究者的关注，但仍存在节点定位误差大、算法定位精度低的缺点。而文献[15]先利用DV-Hop定位算法计算出未知节点的坐标，然后利用一个能够判断节点之间关系的优化模型来删除定位误差较大的坐标，进而提高改进算法的定位精度；文献[16]中未知节点的平均每跳距离值是通过平均网络中所有锚节点的平均每跳距离值而得到的，使用此策略提高了DV-Hop定位算法的定位精度；文献[17]中锚节点使用两种通信半径广播数据分组来计算自己与未知节点的最小跳数与距离，在经典DV-Hop定位算法的基础上降低了节点的定位误差；文献[18]将网络中的未知节点模拟成锚节点来进行DV-Hop定位，该方法虽然增加了累积误差但相比于定位误差的增加定位精度的提高更明显。以提高算法的定位精度为目的，出现了以上等参考文献对经典DV-Hop定位算法的改进，但仍然存在很多不足。本文将从经典DV-Hop定位算法存在较大定位误差的问题出发，结合多种方法对DV-Hop定位算法进行改进并仿真证明降低了节点的定位误差、提高了算法的定位精度。

2 DV-Hop定位算法

首先，确定最小跳数。所有锚节点向网络中广播带有跳数字段和锚节点位置信息的数据分组，通过该过程网络中每个传感器节点都知道了自己到每个锚节点之间的最小跳数和每个锚节点的位置信息。

其次，确定跳段距离。网络中锚节点的平均每跳距离计算公式为

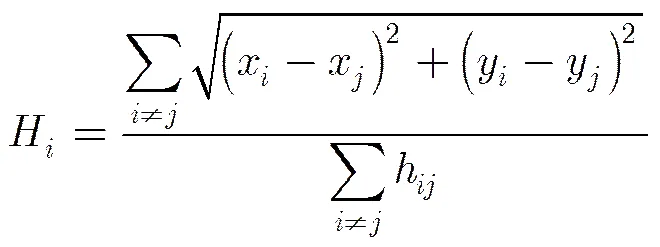
然后，所有锚节点向网络中广播自己的平均每跳距离信息，未知节点就把最先接收到的那个锚节点的平均每跳距离当做自己的平均每跳距离。未知节点用自己到某一个锚节点的最小跳数乘以自己的平均每跳距离作为自己到该锚节点的跳段距离。

最后，确定未知节点坐标。根据未知节点与每个锚节点的跳段距离以及锚节点的位置信息，利用极大似然估计法或三边测量法计算未知节点的坐标。

3 WSGDV-Hop定位算法

随着WSN定位算法研究的不断发展[19,20]，算法简单且网络能耗小、成本低的DV-Hop定位算法更是学者们的研究热点[21]。本文从经典DV-Hop定位算法存在误差的几个方面出发进行算法改进，提出了一种基于误差距离加权与跳段算法选择的遗传优化DV-Hop定位算法(WSGDV-Hop)。

3.1 未知节点平均每跳距离的确定

在经典DV-Hop定位算法中未知节点将最先接收到的锚节点的平均每跳距离作为自己的平均每跳距离，然而该方法存在一定的问题，如：一旦唯一接收的锚节点平均每跳距离存在很大的误差，就会使未知节点的平均每跳距离存在很大的误差，则之后一切基于未知节点平均每跳距离的计算都是误差的不断累积，导致定位误差越来越大；而未知节点的平均每跳距离是用于计算与周边网络内节点的跳段距离的，因此只有一个距离未知节点最近的锚节点的平均每跳距离无法代表未知节点周边网络的情况，且距离未知节点越近的锚节点越能代表未知节点周边网络的情况。综上，考虑以上两点因素后以减小定位误差为目的，在改进算法中未知节点需要考虑多个锚节点的平均每跳距离，且以锚节点平均每跳距离误差越小距离未知节点越近越能代表未知节点平均每跳距离为原则。WSGDV-Hop改进算法中未知节点的平均每跳距离具体计算过程如下：

首先，所有锚节点向网络中广播带有跳数字段和锚节点坐标的数据分组，广播结束后网络中任意两节点间的最小跳数以及锚节点的坐标已知，因此可以计算出锚节点的平均每跳距离：

得知了网络中所有锚节点的平均每跳距离后，开始计算每个锚节点的平均每跳距离误差。首先计算锚节点与之间的跳段距离即计算距离：

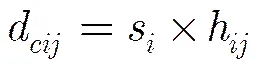
然后计算锚节点与之间的实际距离：

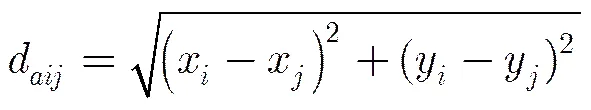
最后计算锚节点的平均每跳距离误差：

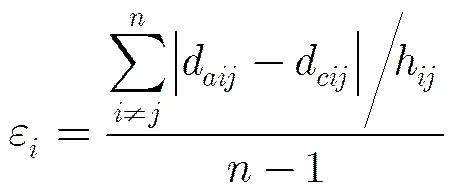
锚节点以广播的形式将计算得到的自身平均每跳距离和平均每跳距离误差向网络进行广播。未知节点以锚节点距离自己越近平均每跳距离误差越小越重要为原则，对接收到的个锚节点的平均每跳距离误差和距离未知节点的跳数距离进行处理计算每个锚节点的权值：

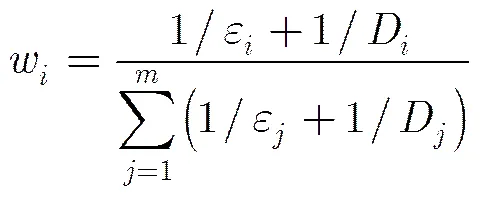
由于未知节点以距离自己越近越重要为原则，所以未知节点接收距离自己最近的个锚节点的信息，其中的取值不宜过大否则接收的过多网络能耗会增加，其次距离未知节点远的锚节点就不能很好地反映未知节点周围的网络了，所以根据仿真试验可以确定的最佳取值为3。

最后，未知节点对接收到的最近的3个锚节点的平均每跳距离做基于权值w的归一化加权处理来计算自己的平均每跳距离：

3.2 未知节点与锚节点间跳段距离的确定

在经典DV-Hop定位算法中未知节点用自己的平均每跳距离乘以距离锚节点的最小跳数来计算彼此间的跳段距离，该方法用跳段距离估计彼此间的直线距离本身就是一个估计值存在误差，然而除此估计误差外该方法还有一定的问题：在计算未知节点与锚节点间跳段距离时应该考虑该锚节点的信息，且网络中有距离未知节点越近的锚节点越能很好地反映它周边网络的原则，所以在计算未知节点与距离自己较近的锚节点间跳段距离时可以根据经典算法计算，因为此时的未知节点平均每跳距离中既涵有该锚节点的信息又有距离未知节点最近的锚节点的信息；当计算与距离自己较远的锚节点间跳段距离时，由于经典算法中未知节点的平均每跳距离中不涵有该锚节点的信息只有距离未知节点最近的锚节点的信息而不适用，应该考虑该锚节点的信息。综上，在改进算法中可以把未知节点周边的锚节点简单的分为距离自己最近的锚节点和非最近的锚节点，然后根据节点位置关系的不同选择不同的跳段距离计算方法来确定彼此间的跳段距离，计算中都要既考虑最近的锚节点的信息又考虑该锚节点的信息。WSGDV-Hop改进算法中未知节点与锚节点间跳段距离的具体计算过程如下：

首先，在图1中，判断节点间的位置关系将需要定位的未知节点周边的锚节点分为距离自己最近的锚节点和非最近的锚节点，其中最近的锚节点只有一个，其它均为非最近的锚节点。

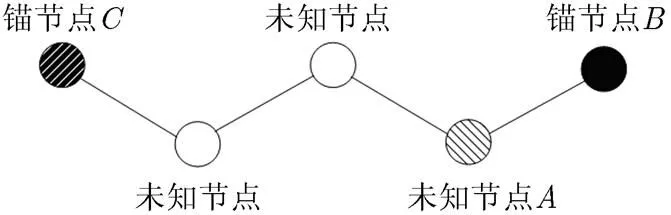
图1 WSGDV-Hop跳段距离计算中锚节点位置判断

其次，针对距离未知节点最近的锚节点，二者间的跳段距离计算公式为

最后，针对距离未知节点非最近的锚节点，二者间的跳段距离计算公式为

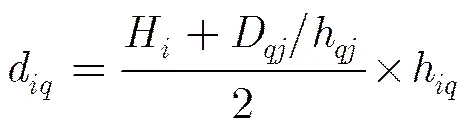
3.3 未知节点坐标的确定

在经典DV-Hop定位算法中，得知未知节点与锚节点间的跳段距离后，采用三边测量法或极大似然估计法计算未知节点坐标，然而使用以上两种坐标计算方法计算得到的未知节点坐标都存在无可避免的误差。因此，在改进算法中引入优化的概念，挑选一个适合的优化模型对以上两种方法计算得出的带有误差的未知节点坐标进行优化，减小未知节点的定位误差。WSGDV-Hop改进算法中未知节点坐标的确定过程如下：首先，根据上文计算得出的未知节点与网络中所有锚节点间的跳段距离，采用极大似然估计法计算未知节点坐标(,)。然后，用改进的遗传算法对未知节点坐标(,)进行优化处理，最后得出未知节点坐标的最优解。

3.3.1 WSGDV-Hop定位算法中遗传算法的改进

为了有效地把遗传算法结合到WSGDV-Hop定位算法中，在经典遗传算法基础上做了些许改进以适应改进算法并更好地优化未知节点坐标，改进遗传算法基本要素及关键参数设置如下：

(1)染色体与初始种群的确定： 把所有未知节点坐标组成的问题空间内的每一个未知节点坐标(,)转换成遗传算法所能处理的染色体，未知节点坐标(,)中的,转化成染色体中的1,2，具体为

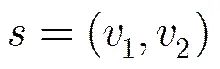
(2)适应度函数的确定： 在WSGDV-Hop定位算法中问题空间的目标函数即未知节点坐标定位误差为

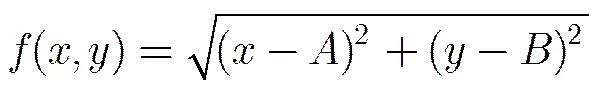
改进遗传算法把问题空间的目标函数作为自己的适应度函数，其值越小，染色体适应力越强，被遗传下去的可能性越高，而不是适应度函数值越大适应能力越强，适应度函数为

(3)交叉算子： 改进遗传算法的交叉算子为

(4)变异算子： 针对遗传算法中变异算子的设计，改进遗传算法与经典遗传算法一致，其计算式为

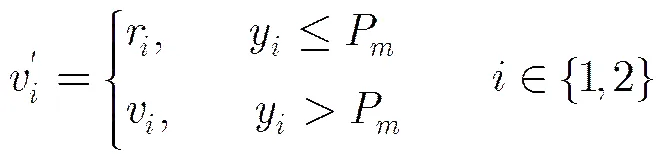
(5)选择算子： 改进遗传算法中选择操作作用于种群中的每一个染色体即每一个号位的染色体，比较染色体和经过交叉、变异后生成的染色体的适应度函数值大小，并选择适应度函数值大的染色体保留到该染色体号位上，完成一代遗传操作过程，而不是在种群中横向比较并选择若干适应度函数值大的染色体遗传下去，改进遗传算法一定要保留每一个号位上的染色体。

4 算法仿真结果

4.1 仿真场景

使用MATLAB仿真比较经典DV-Hop定位算法与WSGDV-Hop定位算法的性能指标，表1为算法对比仿真参数。

表1仿真参数

参数名称取值 网络区域(m2)100100 节点总数100 锚节点数量5, 10, 15, 20, 25, 30, 35, 40 通信半径(m)25, 30, 35, 40, 45 仿真次数总计300 初始种群P0X 交叉概率Pc0.9 变异概率Pm0.07 终止代数T100

4.2 性能评价指标

在WSN中衡量一个定位算法性能好坏的基本指标主要包括：算法的定位精度和节点的平均定位误差，具体计算公式如下：

算法的定位精度：

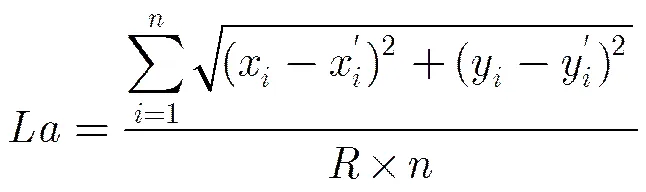
节点的平均定位误差：

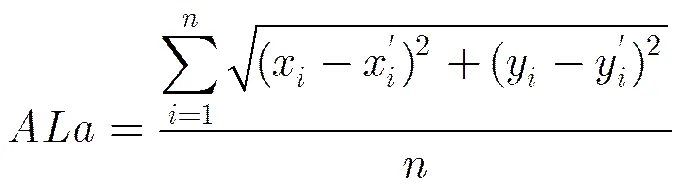
4.3 仿真与分析

图2为WSN网络的拓扑结构图，图中100个传感器节点随机地部署在100 m×100 m的监测区域内，其中的70个黑色圆点是网络中的未知节点，30个五角星是网络中的锚节点。在仿真实验中网络中传感器节点的总数始终为100，而锚节点与未知节点的个数是可以随着实验而确定的。

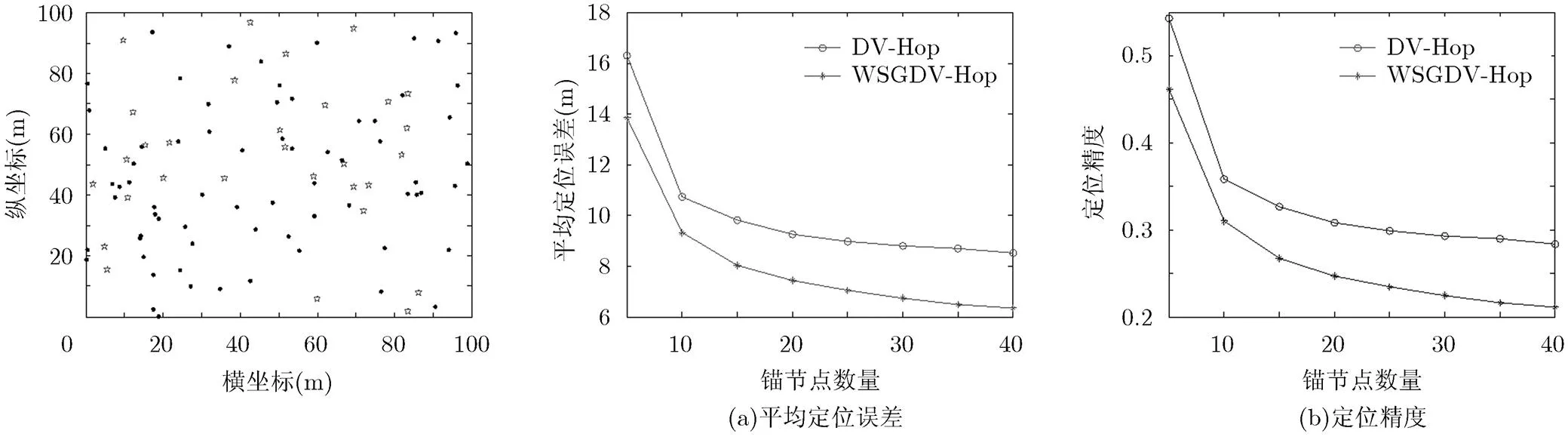
图2 网络拓扑结构图　　　　　　　图3 通信半径R=30 m时WSGDV-Hop与DV-Hop定位算法对比

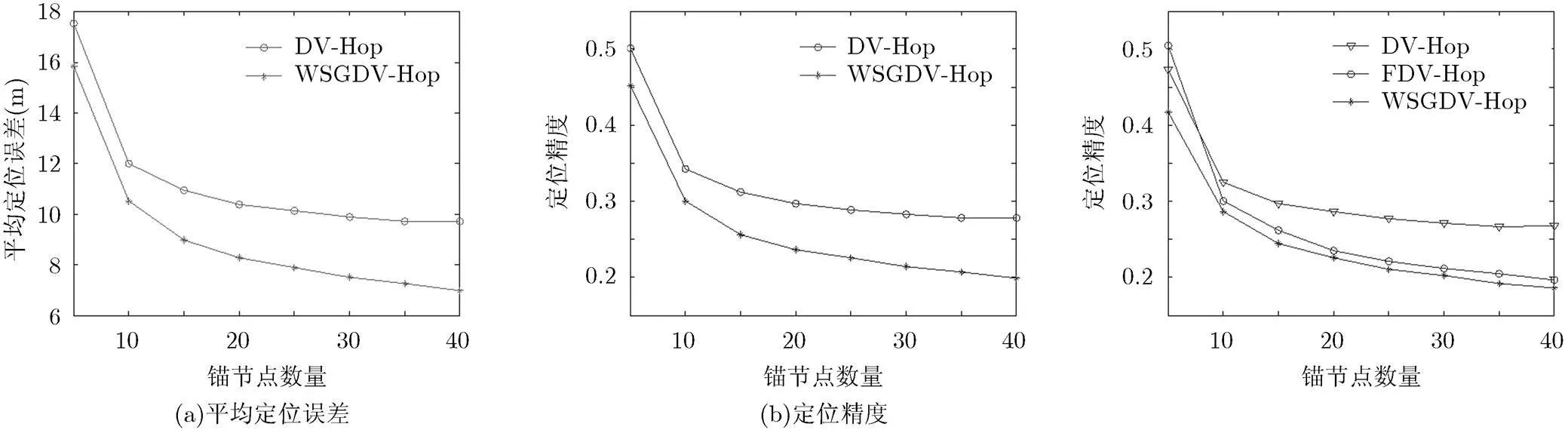
图4 通信半径R=35 m时WSGDV-Hop与DV-Hop定位算法对比　     　图5 通信半径R=40 m时WSGDV-Hop FDV-Hop与DV-Hop算法的定位精度对比

5 结束语

针对DV-Hop定位算法存在较大定位误差的问题，以减小DV-Hop定位算法的节点定位误差，提高算法的定位精度为目的，本文从经典DV-Hop定位算法存在误差的几个方面出发进行算法改进，提出了一种基于误差距离加权与跳段算法选择的遗传优化DV-Hop定位算法，即WSGDV-Hop定位算法。改进算法包括3个改进点：用基于误差与距离的权值处理锚节点的平均每跳距离来确定未知节点的平均每跳距离；根据判断的位置关系选择适合的跳段距离计算方法来确定未知节点与锚节点间的跳段距离；用改进的遗传算法优化未知节点坐标来确定未知节点坐标的最优解。仿真结果表明，WSGDV-Hop定位算法的性能明显优于DV-Hop定位算法，达到了减小节点定位误差、提高算法定位精度的目的。

[1] 钱志鸿, 王义君. 面向物联网的无线传感器网络综述[J]. 电子与信息学报, 2013, 35(1): 215-227.

Qian Zhi-hong and Wang Yi-jun. Internet of things-oriented wireless sensor networks review[J].&, 2013, 35(1): 215-227.

[2] Cheng X, Thaeler A, Xue G,.. TPS:A time-based positioning scheme for outdoor wireless sensor networks[C]. Proceedings-IEEE INFOCOM, Hong Kong, 2004: 2685-2696.

[3] Niculescu D and Nath B. Ad hoc positioning system(APS) using AOA[C]. IEEE INFOCOM 2003: The Conference on Computer Communications, San Francisco, 2003: 1734-1743.

[4] Naeimi Soroush, Chow Chee-onn, and Ishii Hiroshi. Directional multi-hop clustering routing protocol for wireless sensor networks[J]., 2013, 14(2): 123-134.

[5] Girod L and Estrin D. Robust range estimation using acoustic and multimodal sensing[C]. IEEE International Conference on Intelligent Robots and Systems, Hawaii, 2001: 1312-1320.

[6] Radhika Nagpal, Howard Shrobe, and Jonathan Bachrach. Organizing a global coordinate system from local information on an Ad hoc sensor network[C]. 2nd International Workshop on Information Processing in Sensor Networks (IPSN '03), Palo Alto, 2003: 1-16.

[7] Niculescu D and Nath B. DV based positioning in Ad hoc networks[J]., 2003, 22(1~4): 267-280.

[8] Bahl Paramvir and Padmanabhan Venkata N. RADAR: an in-building RF-based user location and tracking system[C]. Proceedings-IEEE International Conference on Computer Communications, Tel Aviv, 2000: 775-784.

[9] Bulusu N, Heidemann J, and Estrin D. GPS-less low cost outdoor localization for very small devices[J]., 2000, 7(5): 28-34.

[10] Nagpal R. Organizing a global coordinate system from local information on an amorphous computer[R]. Artificial Intelligence Memo 1666, MIT Artificial Intelligence Laboratory,Massachusetts, 1999.

[11] Kumar Shrawan and Lobiyal D K. An advanced DV-Hop localization algorithm for wireless sensor networks[J]., 2013, 71(2): 1365-1385.

[12] Hu Yu and Li Xue-mei. An improvement of DV-Hop localization algorithm for wireless sensor networks[J]., 2013, 53(1): 13-18.

[13] Safa Haidar. A novel localization algorithm for large scale wireless sensor networks[J]., 2014, 45(7): 32-46.

[14] Jia Song-hao and Yang Cai. Sub-regional DV-Hop localization algorithm for dynamic anchor nodes[J]., 2013, 51(22): 162-170.

[15] 刘影, 钱志鸿, 王雪. 基于到达时间差的无线传感器网络质心定位算法[J]. 吉林大学学报(工学版), 2010, 40(1): 245-249.

Liu Ying, Qian Zhi-hong, and Wang Xue. Wireless sensor network centroid localization algorithm based on time difference of arrival[J].(),2010, 40(1): 245-249.

[16] Chen Hongyang, Karo Sezaki, Deng Ping,. An improved DV-hop localization algorithm for wireless sensor networks[C]. IEEE Conference on Industrial Electronics and Applications (ICIEA2008), Singapore, 2008: 1557-1561.

[17] 李娟, 刘禹, 钱志鸿. 基于双通信半径的传感器网络DV-Hop定位算法[J]. 吉林大学学报(工学版), 2013, 44(2): 502-507.

Li Juan, Liu Yu, and Qian Zhi-hong. Improved DV-Hop localization algorithm based on two communication ranges for wireless sensor network[J].(),2013, 44(2): 502-507.

[18] Liu Peng-xi, Zhang Xin-ming, Tian Shuang,. A novel virtual anchor node-based localization algorithm for wireless sensor networks[C]. Sixth International Conference on Networking (ICN’07), Martinique, 2007: 9.

[19] Rashid Haroon and Turuk Ashok Kumar. Localization of wireless sensor networks using a single anchor node[J]., 2013, 72(2): 975-986.

[20] Lazaro A, Girbau D, and Moravek P. A study on localization in wireless sensor networks using frequency diversity for mitigating multipath effects[J]., 2013, 19(3): 82-87.

[21] 嵇玮玮, 刘中. DV-Hop定位算法在随机传感器网络中的应用研究[J]. 电子与信息学报, 2008, 30(4): 970-974.

Ji Wei-wei and Liu Zhong. Study on the application of DV-hop localization algorithms to random sensor networks[J].&, 2008, 30(4): 970-974.

[22] 刘影. 无线传感器网络节点定位算法研究[D]. [博士论文], 吉林大学, 2011.

Liu Ying. Study on node localization algorithms in wireless sensor network[D]. [Ph.D. dissertation], Jilin University, 2011.

Genetic Optimization DV-Hop Localization Algorithm Based on Error Distance Weighted and Hop Algorithm Selection

Cheng Chao Qian Zhi-hong Fu Cai-xin Liu Xiao-hui

(,,130012,)

For the problem of larger location error in Distance Vector-Hop (DV-Hop) localization algorithm, a genetic optimization DV-Hop localization algorithm based on error distance weighted and hop algorithm selection is proposed, namely WSGDV-Hop localization algorithm. The average every hop distance of anchor nodes is weighted by the error and the distance, the hop distance calculation method between unknown nodes to anchor nodes is selected by position judgment, and the calculated unknown nodes coordinates are optimized by improved genetic algorithm. The simulation results show that WSGDV-Hop localization algorithm achieves better performance than DV-Hop localization algorithm, the node location error is reduced, and the location accuracy is increased.

Wireless Sensor Network (WSN); Genetic algorithm; Normalized weighted; Distance Vector-Hop (DV-Hop) localization algorithm; Judgment selection

TP393

A

1009-5896(2015)10-2418-06

10.11999/JEIT141205

2014-09-15；改回日期：2015-06-24；

2015-07-17

钱志鸿 dr.qzh@163.com

国家自然科学基金(61401175, 61371092)

The National Natural Science Foundation of China (61401175, 61371092)

程 超： 男，1984年生，博士生，研究方向为短距离无线通信路由及定位技术.

钱志鸿： 男，1957年生，教授，博士生导师，研究方向为无线网络通信理论及技术.

付彩欣： 女，1988年生，硕士生，研究方向为无线传感器定位技术.