基于互补自适应噪声的集合经验模式分解算法

蔡 念 黄威威 谢 伟 叶 倩 杨志景



基于互补自适应噪声的集合经验模式分解算法

蔡 念*黄威威 谢 伟 叶 倩 杨志景

(广东工业大学信息工程学院 广州 510006)

经验模式分解(EMD)及其改进算法作为实用的信号处理方法至今仍然缺少严格的数学理论。该文尝试从数学理论上分析集合经验模式分解和自适应噪声集合经验模式分解的重构误差，推导了总体残留噪声的计算公式。针对自适应噪声集合经验模式分解在每一层固有模态分量上仍然存在残留噪声的问题，在分解过程中添加成对的正负噪声分量，提出一种基于互补自适应噪声的集合经验模式分解算法。实验结果表明，相比于集合经验模式分解和自适应噪声集合经验模式分解，所提的方法能够明显地减少每一层固有模态分量中残留的噪声，拥有较好的信号重构精度和更快的分解速度。

经验模式分解；集合经验模式分解；自适应噪声集合经验模式分解；模态混叠

1 引言

经验模式分解(Empirical Model Decomposition, EMD)是由Huang等人[1]于1998年提出的一种适用于非线性、非平稳信号的时频分析方法。该方法提出后得到了众多研究人员的关注，也被广泛应用于各个领域。经验模式分解虽然在分析非线性、非平稳信号中有很多优势，但由于其理论还需完善，至今仍然存在一些问题，例如：端点效应[7,8]、模态混叠等。

发生模态混叠时，不同尺度的信号被分解到同一个固有模态分量(Intrinsic Mode Functions, IMFs)中，严重时无法得到物理意义明确的结果，使EMD分解失去意义[12]。为了解决模态混叠，文献[13]提出了集合经验模式分解(Ensemble EMD, EEMD)。EEMD在分解过程中，通过向信号中不断加入白噪声的方法来解决模态混叠。该方法虽然能较好地改善模态混叠，但对信号进行重构时，信号中残留的剩余噪声较大。为了解决剩余噪声过大的问题，文献[14]提出了互补集合经验模式分解(Complementary EEMD, CEEMD)。随后文献[15]提出了集合经验模式分解的改进方法—基于自适应噪声的集合经验模式分解(Ensemble EEMD with Adaptive Noise, EEMDAN)。与EEMD方法不同，该方法在分解过程中并不是直接添加白噪声，而是添加经EMD分解的限带的噪声分量；该算法除了添加的噪声不同外，对分解过程也进行了改进。实验表明该方法可以减少筛选次数，减小计算量，一定程度上也减少了虚假分量，重构原信号时重构误差大大降低[15]。虽然从分解的整体来看EEMDAN的重构误差很小，但由于集合平均次数的限制，该方法在每一层分解完之后，IMF分量也不可避免地存在残余噪声。

本文尝试从数学理论上分析集合经验模式分解和自适应噪声集合经验模式分解的重构误差，推导总体残留噪声的计算公式。借鉴CEEMD的方法，在EEMDAN分解时向信号中添加成对的正负的白噪声分量，提出一种基于互补自适应噪声的集合经验模式分解算法(EEMD with Complementary Adaptive Noise, EEMDCAN)。

2 集合经验模式分解

EEMD算法是Wu和Huang在充分研究白噪声统计特性[16]后，针对EMD存在模态混叠现象提出的一种改进算法。该算法通过向原信号中多次添加等幅值的随机白噪声改变信号中的极值点分布，使极值点分布更趋均匀，避免了由于间歇性高频分量造成的模态混叠。然后对分解的结果进行集合平均，使得白噪声在多次EMD分解之后相互抵消，有物理意义的IMF分量保留下来。该算法的流程如下：

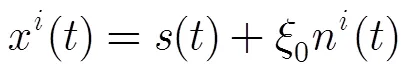
因为EMD分解的完备性，式(2)亦可用等式表示：

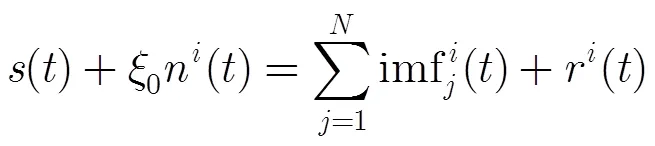
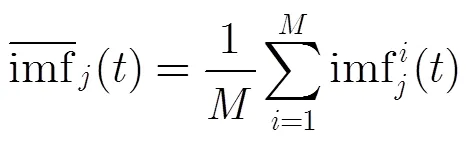
为了分析最后的重构误差，本文将步骤(3)中所得到的个等式相加，可得：

根据高斯白噪声的统计特性，随着集合平均次数的增加，就越趋近于零，重构误差就越小，但增加集合次数又会增加计算量，消耗计算时间。

3 自适应噪声集合经验模式分解

EEMDAN算法[15]对EEMD进行了两方面的改进：第一，在分解过程中并不是直接向信号中添加标准的白噪声，而是添加经过EMD分解的噪声分量(第一阶IMF除外)，该噪声分量的带宽经过了EMD的自适应分割；第二，与EEMD独立分解出各组信号所有的固有模态分量之后再进行集合平均不同，EEMDAN分解出各组信号的第一阶固有模态分量后，立即进行集合平均得到第一阶集合平均固有模态分量，然后从原信号中剔除第一阶集合平均固有模态分量得到一个剩余分量，将该剩余分量作用为新的信号，继续重复上述过程得到第二，第三直到最后一阶模态分量。我们定义一个操作，即信号经过EMD分解后得到的第阶模态分量，为所加噪声的幅值，EEMDAN算法可以描述如下：

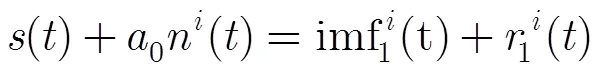
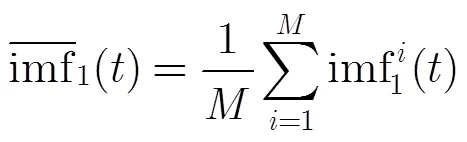
(2)提取第1个模态分量并求出剩余分量：

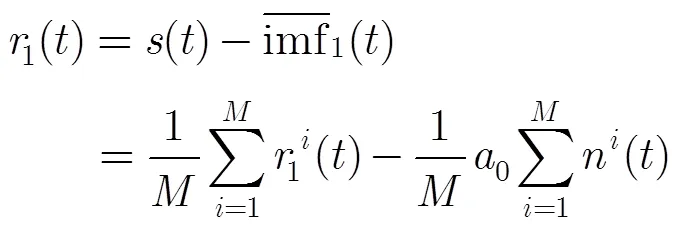
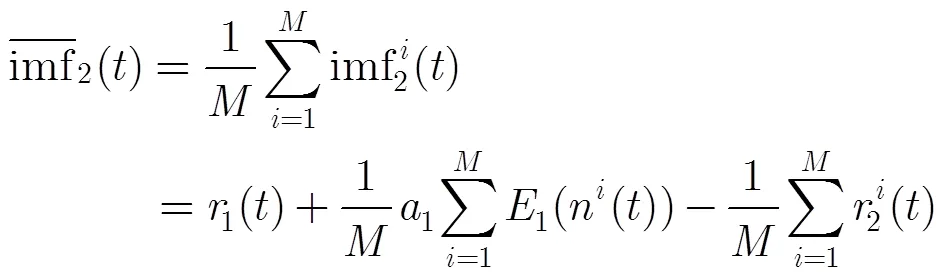
得到剩余分量为

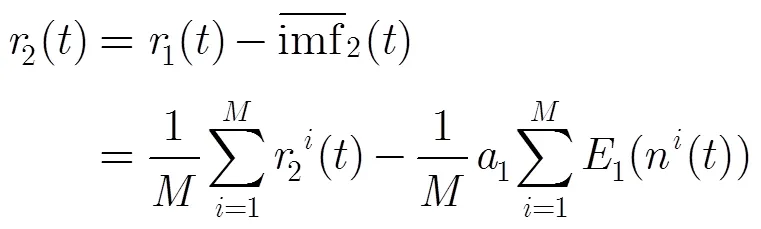
(3)第个剩余分量为

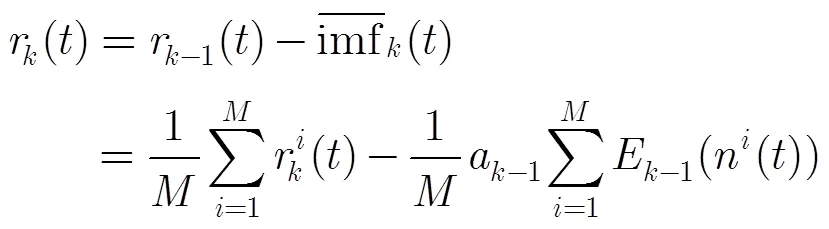
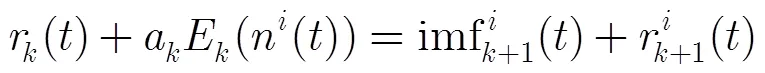
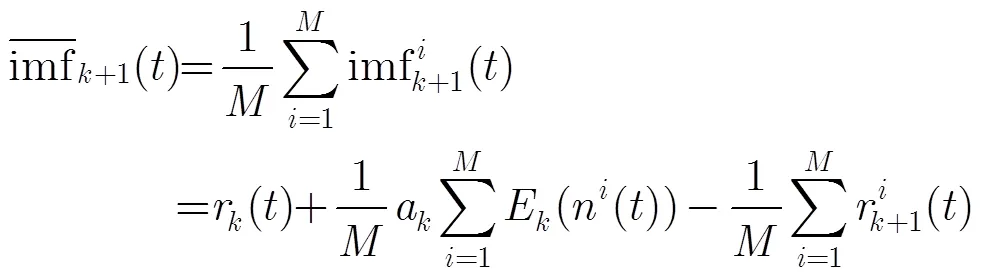
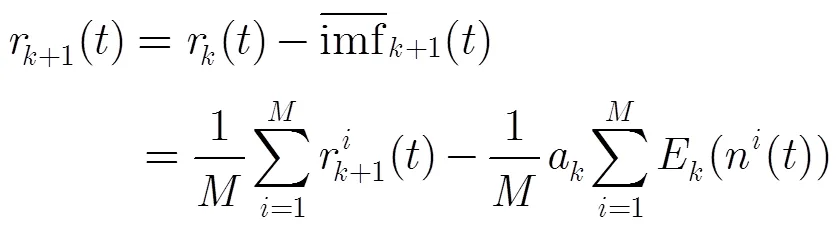
(4)循环进行步骤(3)，直到提取出所有的固有模态分量之后得到剩余分量。

继续分析重构误差，将步骤(1)中所得到的个式(7)相加，可得

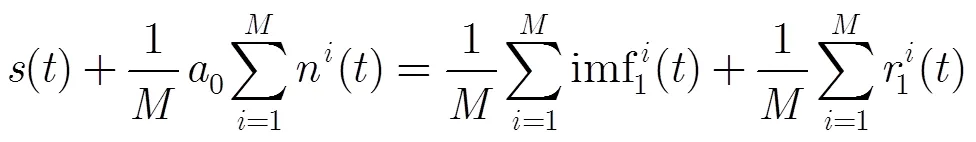
将步骤(2)中所得到的个式(10)相加，可得

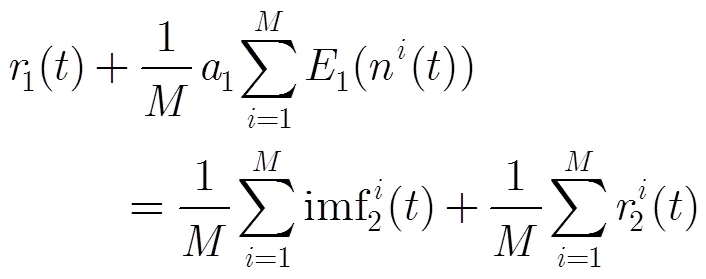
步骤(3)中所得到的个式(14)相加，可得

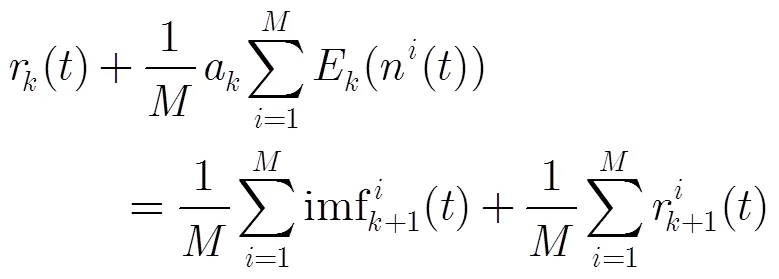
将式(17)，式(18)及式(19)依次迭代相加，并将式(9)，式(12)，式(13)代入等式中可得

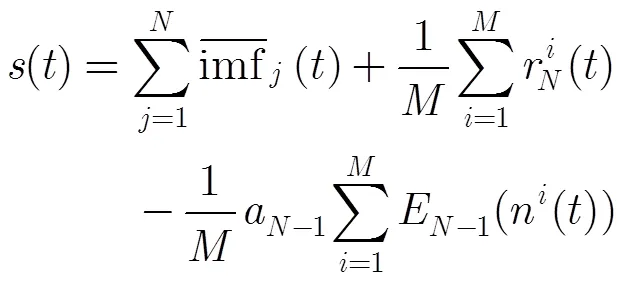
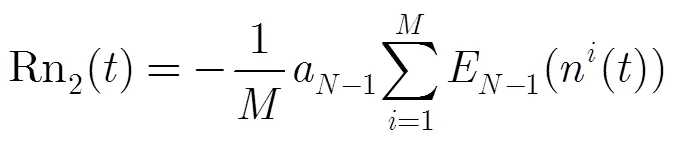
4 互补自适应噪声集合经验模式分解

根据文献[15]和第3节数学理论推导可知，从分解的整体来看在集合平均次数相同的条件下，EEMDAN最终残留噪声比EEMD小，即重构误差比EEMD小。但这并不意味着在每层的局部分解过程中，残留在每个IMF分量中的白噪声分量很小。要减小每层IMF分量中残留的噪声就必须增加集合平均次数，但这样又会增加计算量。为此，我们借鉴CEEMD方法，在EEMDAN分解的基础上提出互补自适应噪声集合经验模式分解，即在每一层的分解过程中成对地添加正负噪声对，其他过程与EEMDAN相同。具体算法如下：

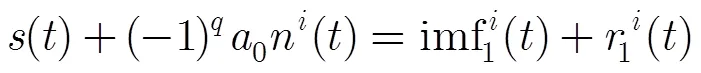
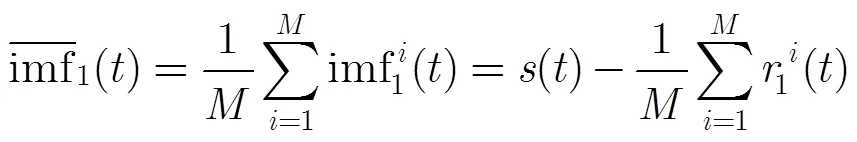
对比式(8)和式(23)，在次集合平均中正负噪声对互相抵消，故可以减小残留在中的噪声。

(2)提取第1个模态分量并求出剩余分量：

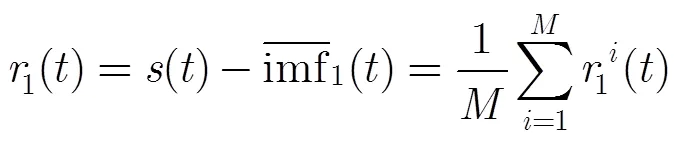
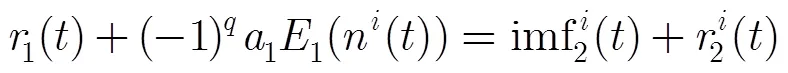
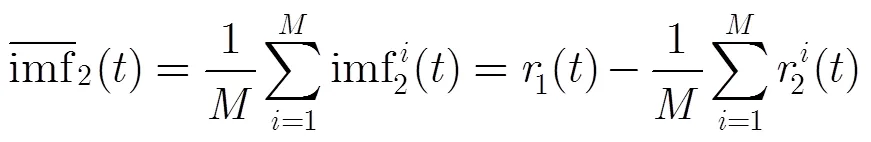
得到剩余分量为

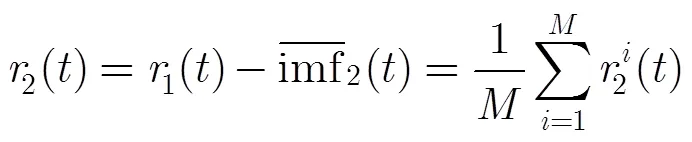
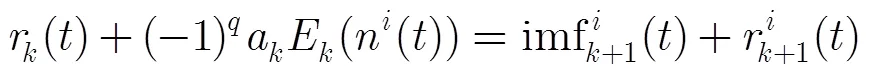
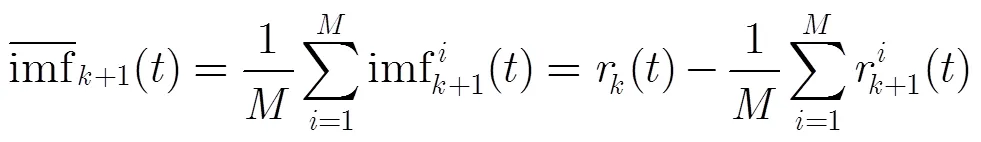
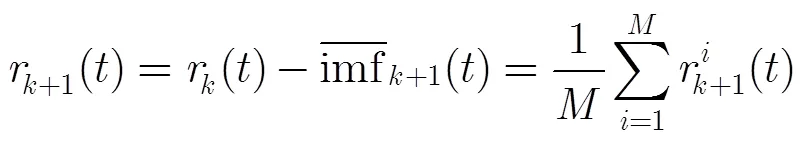
对比式(15)和式(29)，在次集合平均中正负噪声分量对互相抵消，故可以减小残留在中的噪声。

(4)循环进行步骤(3)，直到提取出所有的固有模态分量之后得到剩余分量。

5 实验仿真

选用美国麻省理工学院MIT-BIH Normal Sinus Rhythm Database数据库16265号ECG第一联信号[17]进行分解实验，数据采样率为128 Hz，记录长度为10 s，传感器采集数据时幅值增益为200(幅值单位mV)，ECG信号的波形如图1所示。分解时所加噪声幅值均为信号标准差的0.2倍，EEMD和EEMDAN添加噪声次数为50次，EEMDCAN添加正负噪声对数为25对，分解得到的模态分量如图2所示，图3为本次3种方法分解的重构误差。为了更清楚地比较3种方法分解ECG信号的性能，取出图2中各分解结果的前3个IMF分量及EEMDAN添加噪声次数增加到800次分解得到的前3个分量，如图4所示。

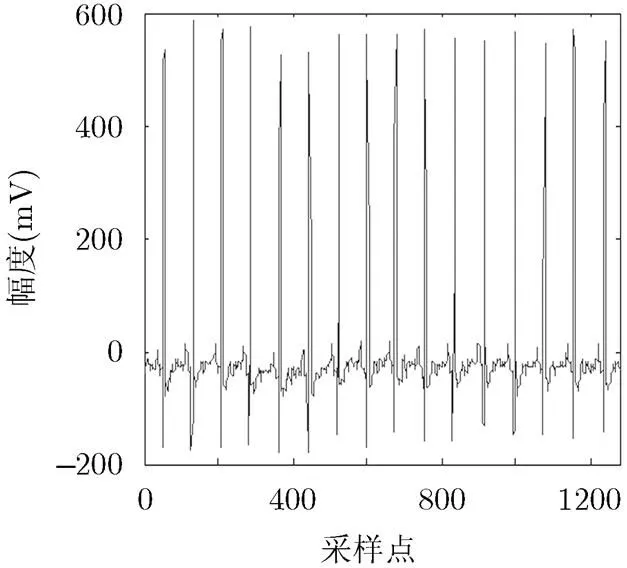
图1 ECG信号的波形图

为了进一步展示EEMDCAN算法的优越性，在上述分解参数的条件下，采用以上3种方法分解该数据库中所有18个ECG第一联信号，并计算所有信号的重构均方根误差(root mean squared error)的均值和方差(如表1)以及分解所需总迭代次数的均值和方差(如表2)。

表1 3种分解方法重构均方根误差的均值和方差

表2 3种分解方法分解ECG信号时总迭代次数的均值和方差

从图2可以看出，对于同一个信号ECG, EEMD, EEMDAN和EEMDCAN分解分别得到12, 11和10个IMF分量，即在添加噪声总次数相同条件下，EEMDCAN得到的虚假分量较EEMD和EEMDAN少。从图3(a)~图3(c)及表1可以看出EEMDAN与EEMDCAN的重构误差大致相等，但比EEMD的重构误差小很多，这与第3节的数学理论分析结论相同。从图4(b)中可以看出EEMDAN虽然从整体上可以比较精确地重构出原信号，但EEMDAN在每一层分解得到的IMF中仍然残留有剩余的噪声分量，只是在重构时各个IMF分量中残留的噪声之和几乎为零而已。对比图4(b)和图4(c)中IMF3分量箭头处的波形可知，在添加噪声总次数相同的条件下(包括正负噪声对)，相对于EEMDAN分解的结果EEMCAN可以明显减小残留在各层IMF分量中的剩余噪声。对比图4(b)和图4(d)可以看出要减小IMF分量中残留的噪声必须增加EEMDAN集合平均次数，但增加集合平均的次数会大大增加计算量。

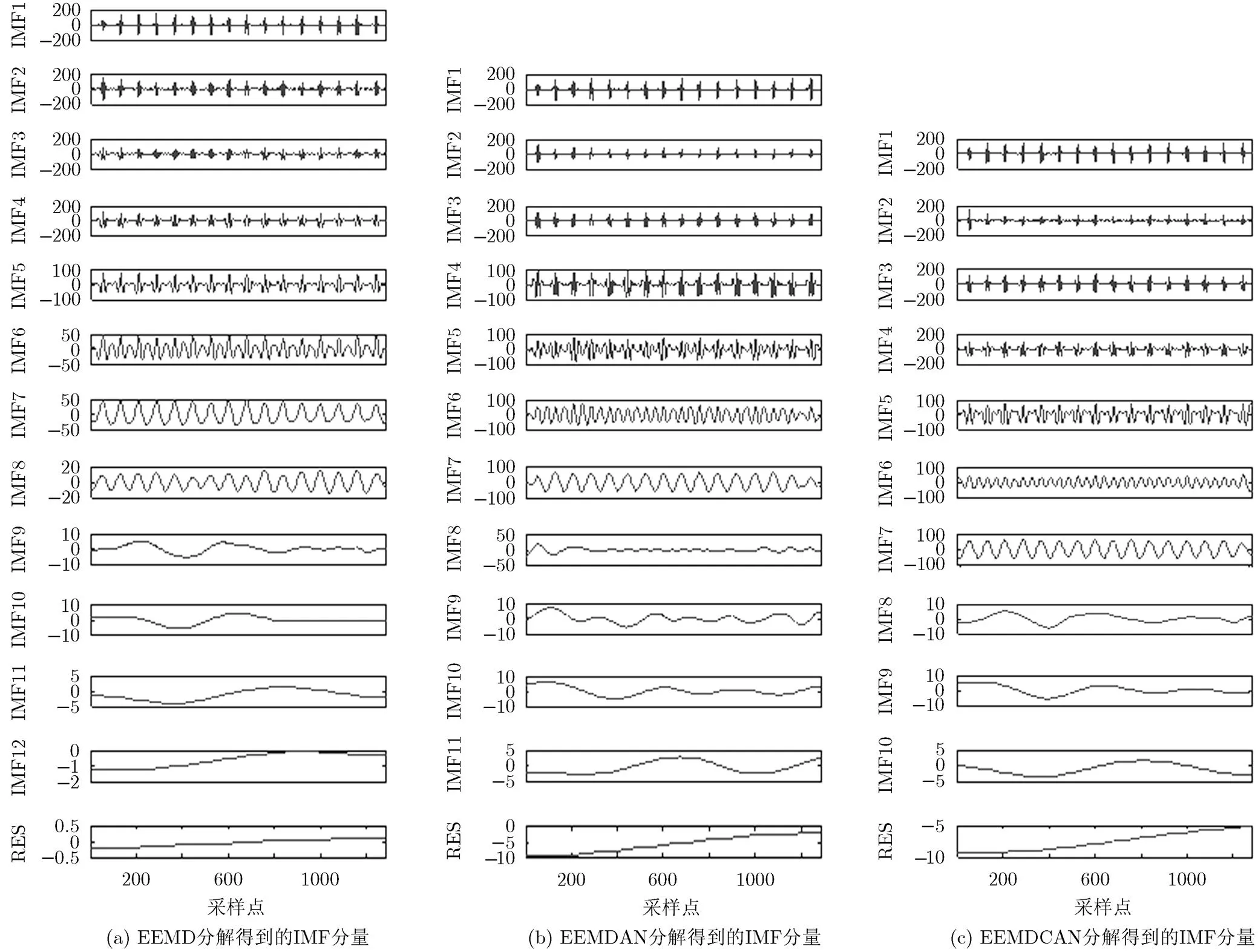
图2 3种分解方法得到的IMF分量

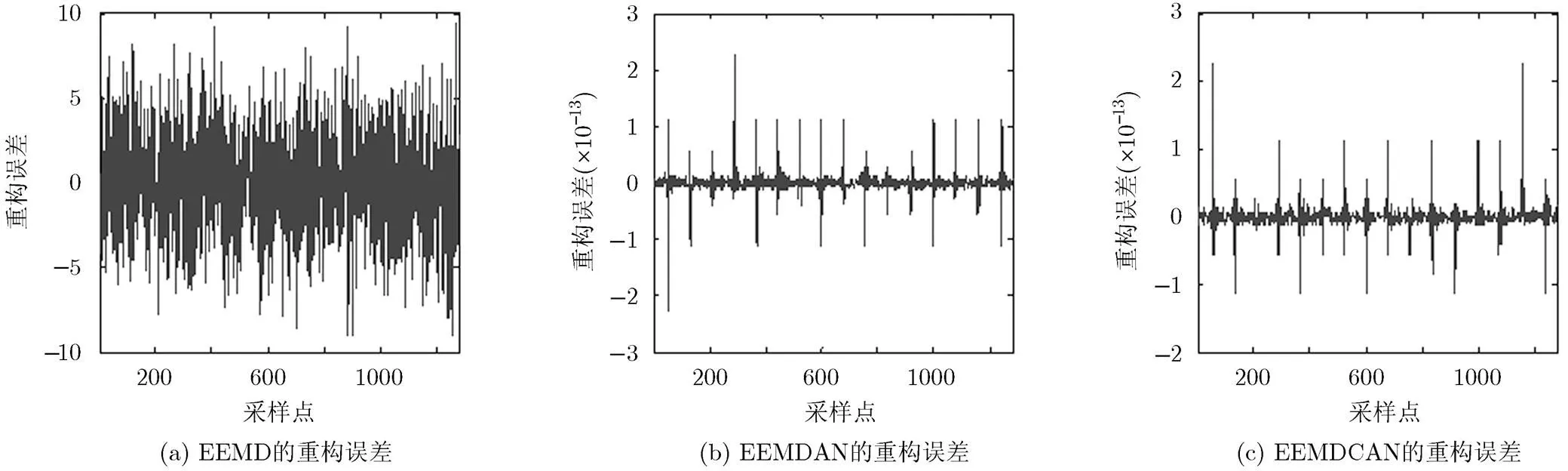
图3 3种分解方法的重构误差

从表2可以看出EEMDAN与EEMDCAN总迭代次数比EEMD分解次数少很多，大大减小了计算量，且EEMDCAN能在不增加计算量的条件下显著减少IMF分量中残留的噪声。

图4 3种分解方法得到的前3个分量

6 结束语

EEMDAN作为EEMD算法的改进方法可以减少筛选迭代次数，减少虚假分量，提高重构精度。但由于集合次数的限制，在每个IMF分量中仍然残留有噪声。本文推导了EEMD及EEMDAN分解后总体残留噪声的计算公式，分析了重构误差。在EEMDAN算法的基础上提出EEMDCAN算法，并应用于ECG信号的分解。实验结果表明EEMD和EEMDAN, EEMDCAN算法可以不用大幅增加集合平均次数的条件下显著减小残留在每个IMF分量的残留噪声，这在生物医学工程应用中具有一定的优势。本文下一步将继续研究利用EEMDCAN算法抑制心电信号中的工频干扰、基线漂移及去噪。

[1] Huang N E, Shen Z, Long S R,.. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]..:,, 1998, 454(1971): 903-995.

[2] Yang Z, Ling B W K, and Bingham C. Trend extraction based on separations of consecutive empirical mode decomposition components in Hilbert marginal spectrum[J]., 2013, 46(8): 2481-2491.

[3] Yang Z, Ling B W K, and Bingham C. Fault detection and signal reconstruction for increasing operational availability of industrial gas turbines[J]., 2013, 46(6): 1938-1946.

[4] 王玉静, 康守强, 张云, 等. 基于集合经验模态分解敏感固有模态函数选择算法的滚动轴承状态识别方法[J]. 电子与信息学报, 2014, 36(3): 595-600.

Wang Yu-jing, Kang Shou-qiang, Zhang Yun,.. Condition recognition method of rolling bearing based on ensemble empirical mode decomposition sensitive intrinsic mode function selection algorithm[J].&, 2014, 36(3): 595-600.

[5] Li H, Wang X, Chen L,.. Denoising and R-peak detection of electrocardiogram signal based on EMD and improved approximate envelope[J].,,, 2014, 33(4): 1261-1276.

[6] 杨达, 王孝通, 徐冠雷. 基于多尺度极值的一维信号趋势项快速提取方法研究[J]. 电子与信息学报, 2013, 35(5): 1208-1214.

Yang Da, Wang Xiao-tong, and Xu Guan-lei. Research on 1D signal fast trend extracting via multi-scale extrema[J].&, 2013, 35(5): 1208-1214.

[7] 白春华, 周宣赤, 林大超, 等. 消除 EMD 端点效应的 PSO-SVM 方法研究[J]. 系统工程理论实践, 2013, 33(5): 1298-1306.

Bai Chun-hua, Zhou Xuan-chi, and Lin Da-chao,.. PSO-SVM method based on elimination of end effectsinEMD[J].-&, 2013, 33(5): 1298-1306.

[8] Lin D C, Guo Z L, An F P,.. Elimination of end effects in empirical mode decomposition by mirror image coupled with support vector regression[J]., 2012, 31: 13-28.

[9] 汤宝平, 董绍江, 马靖华. 基于独立分量分析的EMD模态混叠消除方法研究[J]. 仪器仪表学报, 2012, 33(7): 1477-1482.

Tang Bao-ping, Dong Shao-jiang, and Ma Jing-hua. Study on the method for eliminating mode mixing of empirical mode decomposition based on independent component analysis[J]., 2012, 33(7): 1477-1482.

[10] Shen W C, Chen Y H, and Wu A Y A. Low-complexity sinusoidal-assisted EMD (SAEMD) algorithms for solving mode-mixing problems in HHT[J]., 2014(24): 170-186.

[11] Zheng J, Cheng J, and Yang Y. Partly ensemble empirical mode decomposition: an improved noise-assisted method for eliminating mode mixing[J]., 2014(96): 362-374.

[12] 高云超, 桑恩方, 许继友. 分离EMD中混叠模态的新方法[J]. 哈尔滨工程大学学报, 2008, 29(9): 963-966.

Gao Yun-chao, Sang En-fang, and Xu Ji-you. A new method for separating mixed modes in empirical mode decomposition [J]., 2008, 29(9): 963-966.

[13] Wu Z and Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]., 2009, 1(1): 1-41.

[14] Yeh J R, Shieh J S, and Huang N E. Complementary ensemble empirical mode decomposition: a novel noise enhanced data analysis method[J]., 2010, 2(2): 135-156.

[15] Torres M E, Colominas M A, Schlotthauer G,.. A complete ensemble empirical mode decomposition with adaptive noise[C]. 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech, 2011: 4144-4147.

[16] Wu Z and Huang N E. A study of the characteristics of white noise using the empirical mode decomposition method[J]..:,, 2004, 460(2046): 1597-1611.

[17] Goldberger A L, Amaral L A N, Glass L,.. PhysioBank, Physio Toolkit and PhysioNet: components of a new research resource for complex physiologic signals[J]., 2000, 101(23): E215-E220.

Ensemble Empirical Mode Decomposition Base on Complementary Adaptive Noises

Cai Nian Huang Wei-wei Xie Wei Ye Qian Yang Zhi-jing

(,,510006,)

Empirical Model Decomposition (EMD) and its improved algorithms are most useful signal processing methods. However, those methods still lack rigorous mathematical theory. This paper attempts to analyze mathematically the reconstruction errors for Ensemble EMD (EEMD) and EEMD with Adaptive Noises (EEMDAN). Moreover, the formulae of the residual noise are deduced step by step. There exists the residual noise in each intrinsic mode function during the EEMDAN. To suppress the residual noise, an improved ensemble empirical mode decomposition with complementary adaptive noises by adding pairs of positive and negative noises is proposed. The experimental results indicate that the proposed method can obviously reduce the residual noise in each intrinsic mode function compared with the EEMD and the EEMDAN, and it also has better signal reconstruction precision and faster signal decomposition.

Empirical Model Decomposition (EMD); Ensemble EMD (EEMD); EEMD with Adaptive Noise (EEMDAN); Mode mixing

TN911.7

A

1009-5896(2015)10-2383-07

10.11999/JEIT141632

2014-12-25；改回日期：2015-06-15；

2015-07-17

蔡念 cainian@gdut.edu.cn

国家自然科学基金(61001179, 61471132)，东莞市产学研合作项目(2013509104105)和广州市产学研协同创新重大专项(201508010001)

The National Natural Science Foundation of China (61001179, 61471132); The Project on Integration of Production, Education, and Research, Dongguan, Guangdong Province, China (2013509104105); The Guangzhou Science & Technology Key Project on Collaborative Innovation in Integration of Production, Education, and Research (201508010001)

蔡 念： 男，1976年生，副教授，硕士生导师，主要研究方向为数字信号处理、图像处理、模式识别等.

黄威威： 男，1986年生，硕士，主要研究方向为数字信号处理、DSP开发等.