基于有序样品聚类最优二分割算法的滑坡演化阶段划分

黄 丽，樊孝菊，罗文强



基于有序样品聚类最优二分割算法的滑坡演化阶段划分

黄 丽1,2，樊孝菊1，罗文强2

(1.湖北文理学院数学与计算机科学学院，湖北襄阳 441053；2.中国地质大学(武汉) 数学与物理学院，湖北武汉 430074)

利用有序样品聚类的最优二分割算法，对新滩滑坡检测累计位移数据进行有序聚类划分，再结合加速度变化特征对滑坡演化阶段进行划分. 结果显示新滩滑坡初始变形阶段和中等变形阶段划分点为1979年8月，中等变形阶段和加速变形阶段划分点为1982年9月，而加速变形阶段中初等加速与中等加速的分界点为1983年7月，中等加速与临滑阶段的分界点为1984年10月，与实际监测基本吻合. 表明根据有序样品聚类最优二分割算法和滑坡变形加速度变化特征可以对滑坡演化阶段进行准确划分，并为滑坡预警预报提供依据.

有序样品聚类；最优二分割算法；滑坡演化阶段划分；新滩滑坡

目前，滑坡预报的判断方法种类很多，如许强、曾欲平发现加速度的变化表现出与累计位移和变形速率完全不同的特点，依托大量监测数据，对滑坡从开始变形到失稳破坏的全过程进行系统的分析和研究[1]；金海元设计出适合锦屏一级水电站边坡的综合预测预报模型，初步给定边坡4项预警临界值(位移速率、位移切线角、地震峰值加速度、降雨量)[2]；王尚庆，徐进军，罗勉把滑坡宏观前兆信息与关键部位监测点的变形速率及相关影响因素有机结合和集成的滑坡险情预警综合预报方法[3]等，为滑坡预报提供了可靠地依据，但位移变化是滑坡变形最直接的变化特征，因此滑坡演化阶段划分考虑位移变化是非常有必要的.

由于滑坡处于不同阶段对滑坡累积位移有相应的变化，本文以1978年1月到1985年6月新滩滑坡监测数据为例，利用有序聚类最优二分割算法就直接将滑坡累积位移序列进行有序分类，并结合加速度变化特征对滑坡演化阶段进行划分.

1 有序样品聚类算法原理

有序样品聚类分析[4]是对有序的样品进行分段的统计方法，对个有序样品进行分割，就可能有2-1种分割方法，这每一种分法成为一种分割，在所有的这些分割中，有一种分割使得各段内部之间差异性最小，各段之间差异性最大，这种对个样品分段使组内离差平方和最小的分割方法，称为最优分隔.

1.1 一个变量或指标分割的段内差异

设有个样品对某一个变量(或指标)进行测试，记作. 现需对作分割，记()是分割后的某一个样品段，其段内样品之间的差异用段内极差表示为

1.2 有序样品聚类最优二分割算法模型

若用记号S(2,)表示个样品被分割成2段后段内的总离差和，表示分割点且=1,2,…,-1. 那么上述分割所对应的段内总离差和分别为；；……；……；，其中有1,1=d=0.

若=对应的S(2,)在所有分割对应的段内总离差和S(2,)中最小，即

则S(2,)为最小损失函数，对应分割为有序样品最优二分割.

2 实例应用

新滩滑坡位于长江西陵峡上段兵书宝剑峡出口的北岸，隶属湖北省秭归县，下距宜昌市约72km. 滑坡长近2 000m，上、中、下部分别宽250m，400m、500~800m，面积约为0.75×106m2，总体方量3×107m3；滑坡后壁至河床相对高度差800m左右，向长江倾斜，放纵平均坡度为23°，局部陡缓不一. 新滩滑坡监测数据来源于文献[11]，本文选取其1978年1月到1985年6月共90个月的累计位移监测数据(mm)，根据滑坡变形加速度变化特征利用有序聚类算法进行分类，作新滩滑坡加速度和滑新滩坡累积位移的数据如表1、2，观测曲线如图1、2所示.

表1 新滩滑坡累积位移[11] /mm

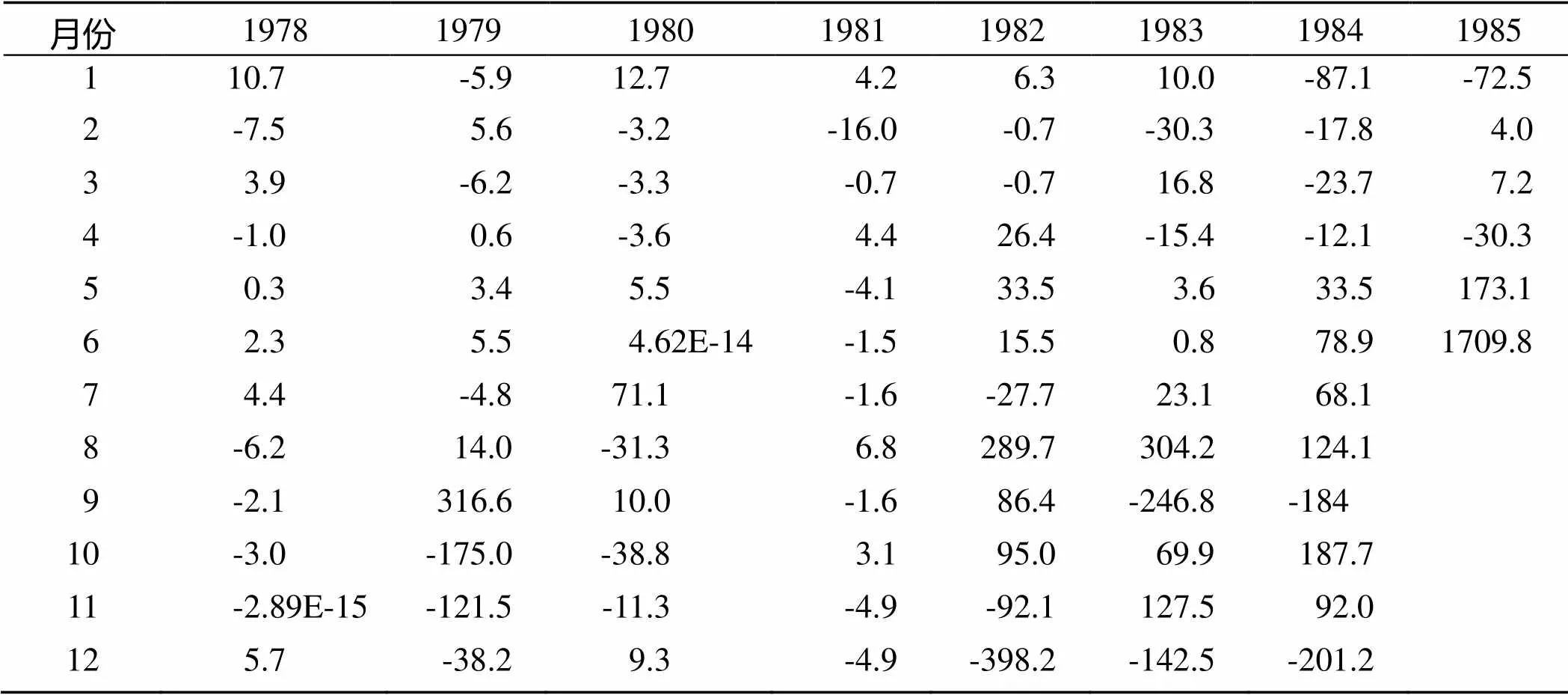
表2 新滩滑坡变形加速度 /(mm×月-2)

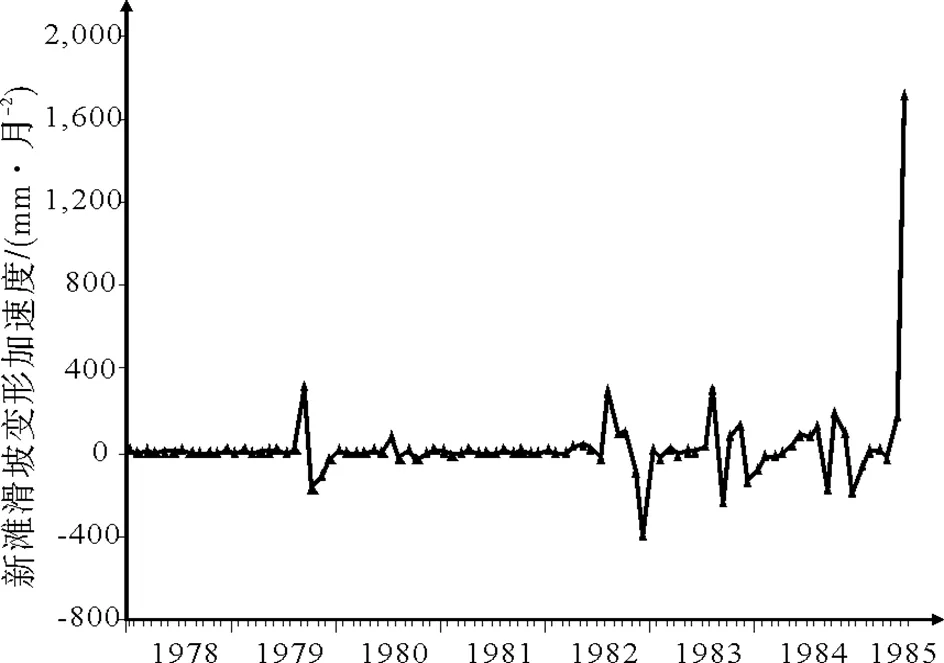
图1 新滩滑坡变形加速度-时间曲线

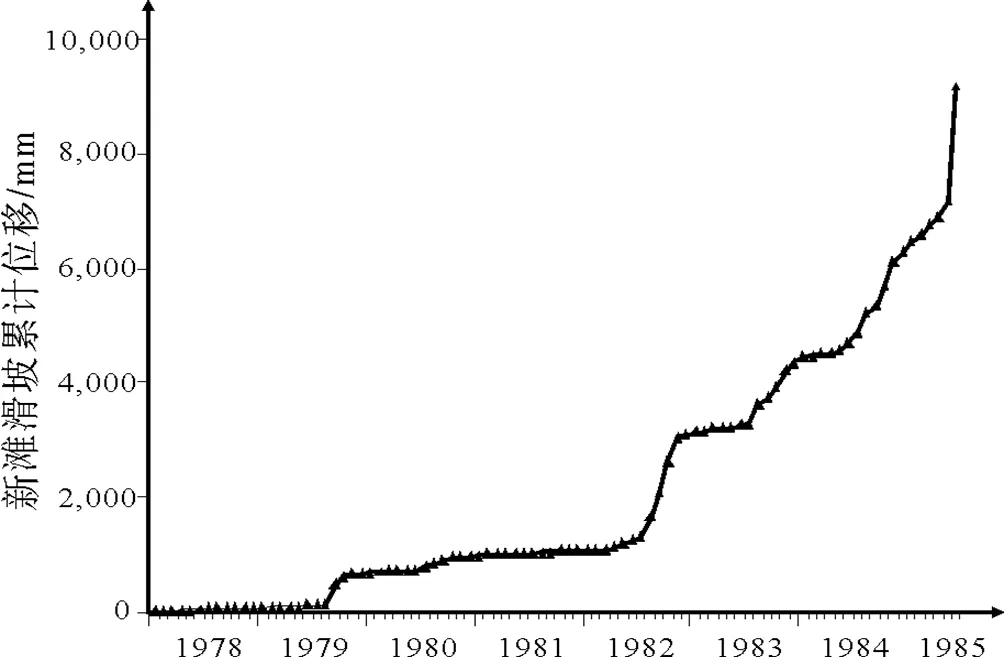
图2 新滩滑坡累计位移-时间曲线

2.1 滑坡初始变形阶段

研究资料表明，加速度在不同演化阶段表现出完全不同的变化特点，在初始变形阶段加速度有一个由0增大到一定值后很快降为0甚至为负值的过程，反映出此阶段滑坡变形突然启动后又迅速减弱的特点[10].

由图2可以看出新滩滑坡的初始变形与加速变形的分界点大致在1979年7月至10月. 选取1978年1月到1979年12月滑坡累计位移数据正则化得

=[0, 0.0049, 0.0156, 0.0249, 0.0346, 0.0478, 0.0677, 0.0782, 0.0855, 0.0882, 0.0909, 0.1023, 0.1048, 0.1157, 0.1172, 0.1196, 0.1272, 0.1432, 0.1518, 0.1817, 0.6923, 0.9371, 0.9976, 1.0000]

对1978年1月到1979年12月滑坡累积位移做二分割，得出最优分割点为20，最小损失函数值

min=24(2,20)=(1,20)+(20,24)=0.4894

与20对应时间点为1979年8月，根据加速度特点将此时间点定为新滩滑坡初等变形与中等变形的分界点.

2.2 滑坡中等变形阶段

在滑坡中等变形阶段，加速度在等速变形阶段主要以0为中心作上下震荡，其均值基本为0. 依据此特征，从图2可以看出滑坡等速变形阶段和加速变形阶段的划分点大致在1982年6月至9月. 选取1980年1月到1982年12月36个滑坡累计位移数据正则化得

=[0, 0.0046, 0.0078, 0.0096, 0.0136, 0.0176, 0.0512, 0.0717, 0.0964, 0.1050, 0.1089, 0.1166, 0.1261, 0.1290, 0.1316, 0.1360, 0.1387, 0.1407, 0.1421, 0.1464, 0.1500, 0.1548, 0.1576, 0.1584, 0.1618, 0.1649, 0.1678, 0.1815, 0.2092, 0.2433, 0.2659, 0.4087, 0.5874, 0.8055, 0.9854, 1.0000]

对1980年1月到1982年12月滑坡累积位移做二分割，得出最优分割点为33，最小损失函数值

min=36(2,33)=(1,33)+(34,36)=0.7819

与33相应时间点为1982年9月，因此将此时间点定为新滩滑坡中等变形与加速变形阶段的分界点.

2.3 滑坡加速变形阶段

在加速变形阶段中，滑坡累积位移又可被划分为初等加速变形阶段、中等加速变形阶段及临滑阶段. 分别选取数据段1983年1月到1983年12月，1984年1月到1985年5月，分别对应的最小损失函数值为

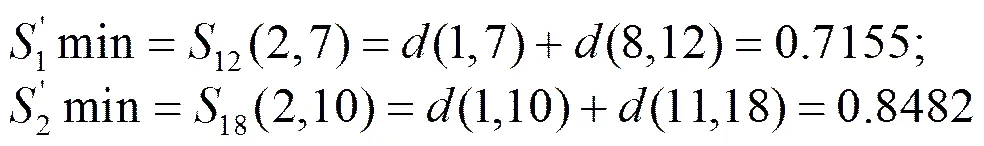
由此可推出初等加速与中等加速的分界点1983年7月，中等加速与临滑阶段的分界点为1984年10月.

综上所述，利用有序样品聚类的最优二分割算法，结合新滩滑坡加速度特征能对滑坡演化阶段进行完整划分(见图3、4). 可以看到，当滑坡从初等变形进入中等变形时，滑坡加速度有一个由0增大到一定值后很快降为0甚至为负值的过程，在相应时间点的滑坡累积位移也有一个较快增长，而随着加速度很快降到零，累积位移增长速度也趋于平缓；当滑坡从中等变形进入加速变形时，滑坡加速度结束以0为中心作上下震荡，呈现一个明显增大过程，在相应时间点的滑坡累积位移也有一个明显增长. 对于滑坡处于初等加速阶段、中等加速阶段、临滑阶段时，其加加速度与滑坡处于初等变形、中等变形、加速变形时的加速度变化特征是类似的. 从图中可以看出有序样品聚类最优分割算法对滑坡演化阶段划分较为准确.

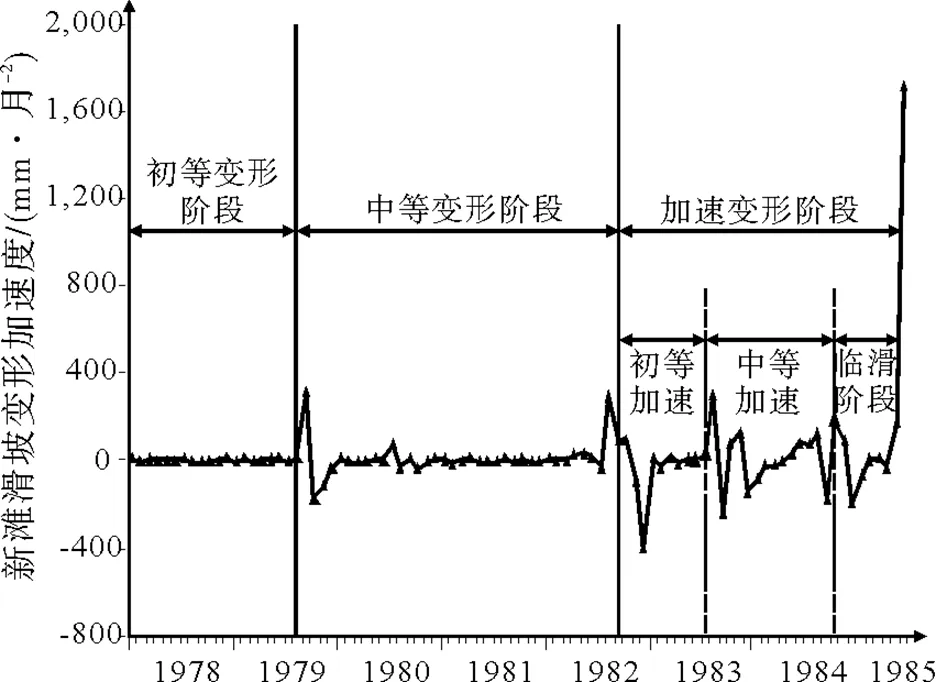
图3 新滩滑坡加速度-时间阶段划分

图4 新滩滑坡累积位移-时间阶段划分

3 结语

滑坡累计位移为有序序列，利用有序样品聚类算法对滑坡累计位移序列进行阶段划分. 根据加速度变化特征，滑坡变形处于某一个变形阶段时，变形加速度处于一个相对稳定的状态，滑坡累计位移也相对稳定；当滑坡从一个阶段进入另一个阶段时，加速度会有一个明显的变化，相应的滑坡累计位移值也会有明显的变化. 因此将使得滑坡累计位移序列段内离差平方和最小(总的离差和一定，段间的平方和最大)的点定为最优分割点具有一定合理性.

有序聚类最优分割算法为滑坡预警预报具有一定参考价值. 但滑坡变形时，滑坡速度、加速度都会有相应变化；而降雨、库水位对滑坡变形也有一定影响，联合多判据划分滑坡演化阶段有待研究.

[1] 许 强, 曾裕平. 具有蠕变特点滑坡的加速度变化特征及临滑预警指标研究[J]. 岩石力学与工程学报, 2009, 28(6): 1099-1106.

[2] 金海元, 徐卫亚, 孟永东, 等. 锦屏一级水电站左岸边坡稳定综合预研究[J]. 岩石力学及工程学报, 2008, 27(10): 2058-2063.

[3] 王尚庆, 徐进军, 罗 勉. 三峡库区白水河滑坡险情预警方法研究[J]. 武汉大学学报: 信息科学版, 2009, 34(10): 1218-1221.

[4] 向东进, 李宏伟, 刘小雅. 实用多元统计分析[M]. 武汉: 中国地质大学出版社, 2005.

[5] 许 强, 黄润秋, 李秀珍. 滑坡时间预测预报研究进展[J]. 地球科学进展, 2004, 19(3): 478-483.

[6] 刘小珊, 罗文强, 李飞翱, 等. 基于SVR的滑坡位移研究[J]. 长江大学学报: 自科版, 2013, 10(4): 76-78.

[7] 杜 鹃, 殷坤龙, 柴 波. 基于诱发因素响应分析的滑坡位移预测模型研究[J]. 岩石力学与工程学报, 2009, 28(9): 1783-1789.

[8] 刘小珊, 罗文强, 李飞翱, 等. 基于关联规则的滑坡演化阶段判识指标[J]. 地质科技情报, 2014, 33(2): 160-164.

[9] 李 聪, 姜清辉, 周创兵, 等. 基于实例推理系统的滑坡预警判据研究[J]. 岩土力学, 2011, 32(4): 1069-1076.

[10] 李远耀. 三峡库区渐进式库岸滑坡的预测预报研究[D]. 武汉: 中国地质大学, 2010.

[11] 周 斌. 新滩滑坡预测预报分析[J]. 路基工程, 2012, 163 (4): 182-185.

Evolution Stages Division of Landslide Based on the Optimal Segmentation Algorithm of Orderly Sample Cluster

HUANG Li1,2，FAN Xiaoju1，LUO Wenqiang2

(1.School of Mathematical and Computer Sciences, Hubei University of Arts and Science, Xiangyang 441053, China; 2.School of Mathematics and Physics, China University of Geosciences, Wuhan 430074, China )

The deformation of landslide from the beginning to the end is divided into three stages, the initial deformation, constant speed deformation and accelerated deformation. The displacement and acceleration of landslide at different stages have different characteristics. The optimal segmentation algorithm of orderly sample cluster is used to divide the stages of Xintan landslide in this paper, August, 1979 is the split point between initial deformation and constant speed deformation, September, 1982 is the split point between constant speed deformation and accelerated deformation, July, 1983 is the split point between initial accelerated deformation and constant accelerated deformation, October 1984 is the split point between constant accelerated deformation and critical sliding stage. The results show that this method can correctly divide the stages of landslide accurately and provide powerful criterion for landslide warning and forecast.

Orderly sample cluster; Optimal two-segmentation algorithm; Evolution stages division of landslide; Xintan landslide

(责任编辑：饶 超)

P642.22；O212.4

A

2095-4476(2015)02-0013-04

2014-11-18;

2014-12-15

国家重点基础发展计划资助973计划(2011CB710605); 国家自然科学基金重点项目(41230637)

黄 丽(1988— ), 女, 湖北襄阳人, 湖北文理学院与中国地质大学(武汉)联合培养硕士研究生.