有限容量模型无标度网络扩散熵分析
龙耀辉
有限容量模型无标度网络扩散熵分析
龙耀辉
(襄阳职业技术学院生物工程学院,湖北襄阳 441000)
利用熵对一类网络交互动力学过程——有限容量模型的网络扩散系统复杂性进行研究,探讨局部拓扑与路由容量这两个关键性因素对其复杂性的影响,并根据熵最大原则确定最优动力学过程的系统参数和高效率路由策略.
有限容量模型;熵;路由容量;局部拓扑;偏向因子
在复杂网络的研究中,深入了解网络拓扑与动力学过程之间的关系一直是其主要理论和实验兴趣之所在. 如何定量描述复杂网络和其上动力学过程的复杂性仍是一个涉及未深的领域. 例如,各种不同动力系统的复杂性,其观测结果是不能完全由其网络拓扑来解释,还与决定动力学过程的规则、参数等因素有关,后者往往也起着更加关键作用. 而且关于网络结构及其上扩散过程的复杂性讨论,一般假定在扩散过程中是没有交互作用的,但事实上,扩散粒子间的交互作用对扩散过程的属性有着不容忽视的影响,其结果导致扩散过程具有更高的复杂性. 一个经典的交互动力学过程例子——有限容量模型如 Zero Range Process(ZRP),其基本原理是实际网络节点仅仅能够传送有限的数据包,在这种机制下讨论有效扩散的最优策略往往需要用到统计力学工具. 不过,依然缺少一种度量交互动力学过程复杂性的方法,即在有限容量机制下如何设计最优扩散过程的方法.
从遍历论的角度来讲,熵是动力系统演化随机性与复杂性的一个度量,将复杂网络与其上的动力学过程通过适当处理,转化为相应的概率空间与保测变换,从而可以用遍历论中的熵去度量其复杂性与随机性. 自此在复杂网络背景下不同关于熵的定义被引入进来,并且用熵去描述复杂网络上动力学过程一般特征的工作逐渐增多. 关于复杂网络熵的讨论已有了一些成果,但主要集中在网络的结构属性(度分布,最短路径等)和网络结构对扩散过程影响方面[1]. 而路由容量是通过路由表来决定包转发路径的,路由表容量指标标志着该路由器可以存储的最多路由表项数量.
本文利用熵这一工具研究有限容量模型网络扩散过程的系统复杂性,并探讨局部拓扑与路由容量这两个关键因素对其复杂性的影响,根据熵最大原则,确定最优动力学过程的系统参数,从而设计出高效率的路由策略.
1 有限容量模型
个粒子初始时随机分布在个节点上,其密度为. 定义各节点处平均出现的粒子数为,定义节点处的跳跃率为,表示该时刻节点处出现的粒子总数. 跳跃率反映了各节点的传输能力,为容量参数. 具体来说,即参数越大,节点具有更大的传输容量,整个网络运行的效率也会更高,此时网络呈现出一个相对活跃的状态. 对于固定的参数,某个节点上的传输效率会随着节点上的粒子数增加而减小,这是因为能够传输的粒子比例会随着粒子总数的增长而下降. 在某一个时刻,每一个粒子是否能够被传输出去取决于跳跃率,若它能跳跃,则它将以一定的概率传输到与之相邻的某个节点上来.
有限容量模型(FC model)上粒子的传输过程可以分为两个阶段,即节点内部粒子之间的竞争机制(节点处理能力有限)和粒子在节点间的传输. 这一动力学过程的交互性就反映在节点内部粒子的竞争机制上,这一机制可以引进跳跃率来定量描述. 对于粒子在节点之间的传输规则,本文采用有偏的随机游走(biased random walk)来描述,即在内部竞争中胜出的粒子从节点传输到与之相邻节点的概率为[3]. 其中参数为偏向因子(biased-factor),越大,粒子更倾向于传输到度大的邻居节点,越小,则倾向于传输到度小的节点. 结合内部竞争机制,节点上的一个粒子下一时刻位于节点的概率[2]为:
本文利用熵研究无标度网络上的交互扩散过程的复杂性与扩散均匀性. 把容量参数(rout-capacity)和偏向因子作为决定有限容量模型上扩散过程的两个关键性参数,研究这两个参数的变化对系统复杂度的影响,通过对参数的优化得到无标度网络上最优最具效率的路由策略.
2 交互扩散过程熵率定义
定义交互扩散过程的熵率[4]为:
在有限容量和随机游走机制下,个粒子在各节点上的分布最终将达到一个稳定状态,一旦能够确定粒子在各节点上的稳态分布,就可以通过式(1)来计算系统的熵率. 为了导出m的表达式,用来表示节点上出现m个粒子时取其权重,其表达式为[5]. 这里是单个粒子以转移概率在网络上游走的稳态概率分布,且.
3 偏随机游走机制下交互动力系统的熵分析
如前所述,在设定机制下粒子在网络上的传输由两个关键因素决定:路由容量与偏向因子. 根据式(1)中熵率定义,研究熵率随着这两个关键因素的变化规律很有意义,由于考虑到偏向因子的作用,关于熵率的理论分析相对困难,故在此仅以数值实验的结果作为分析问题的依据,同时根据最大熵原则,寻找最优传输过程以及由参数和决定的最优路由策略.
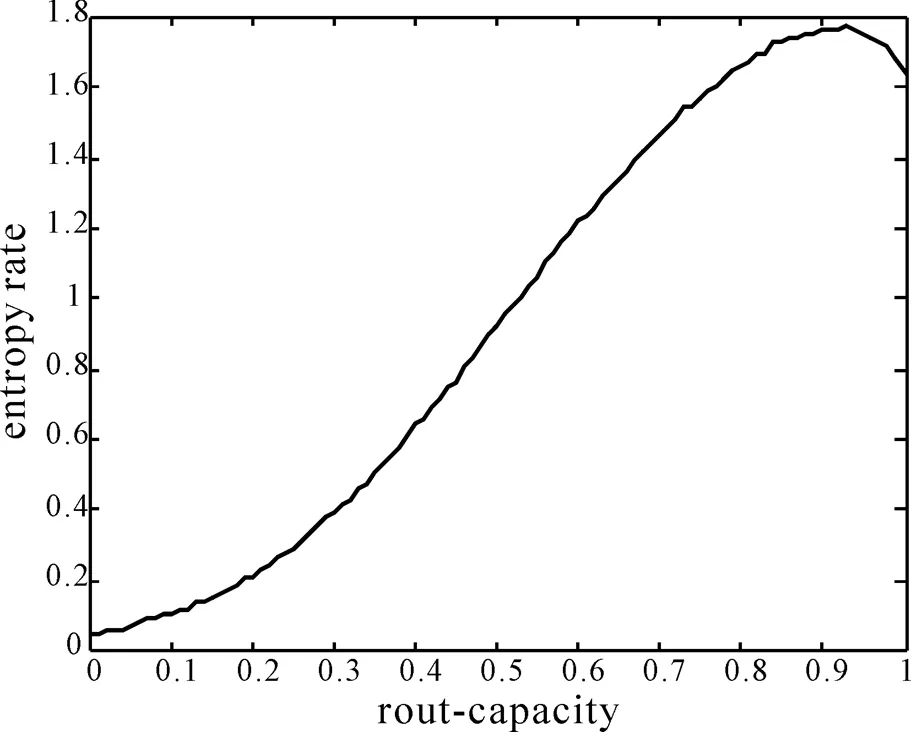
图1 无偏随机游走机制下系统的熵率
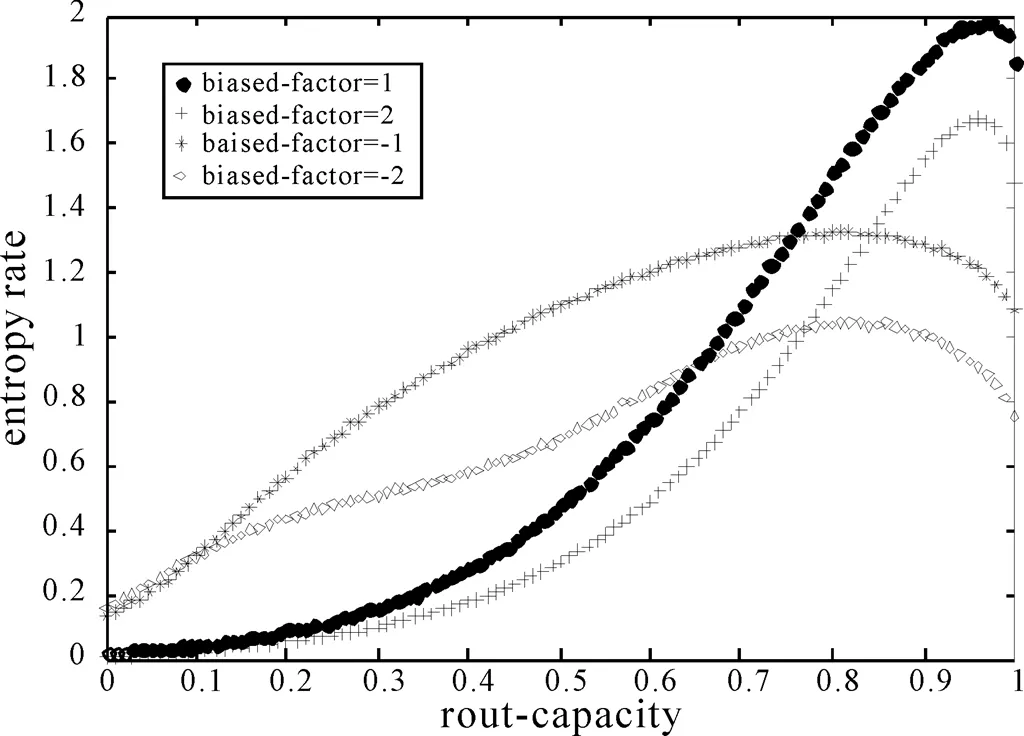
图2 不同偏向因子下的熵率
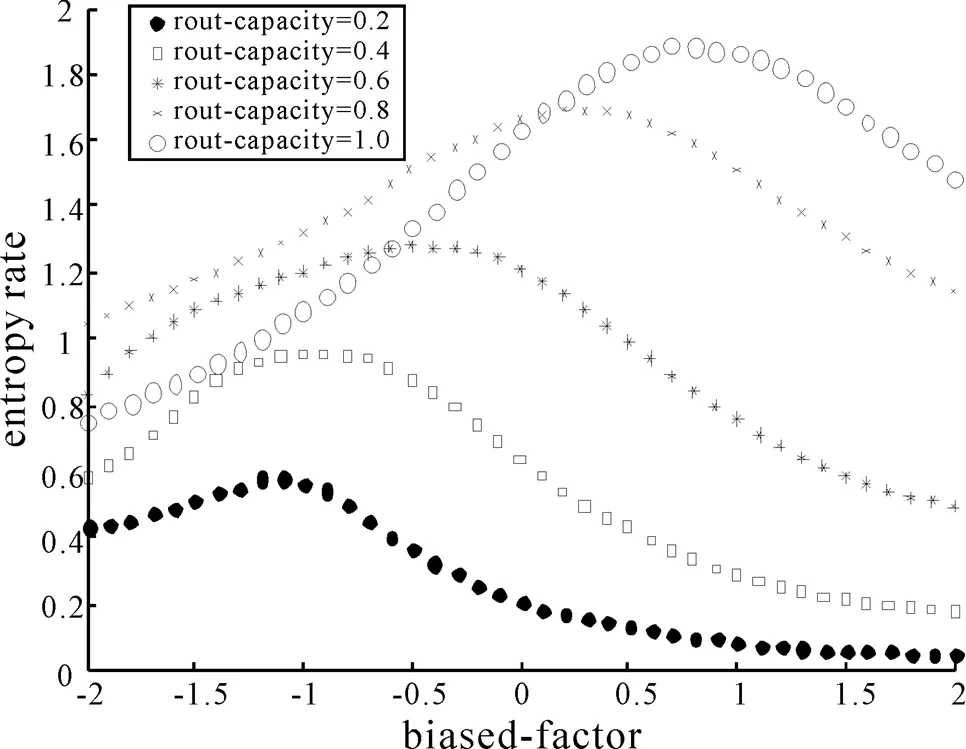
图3不同下熵率随变化散点
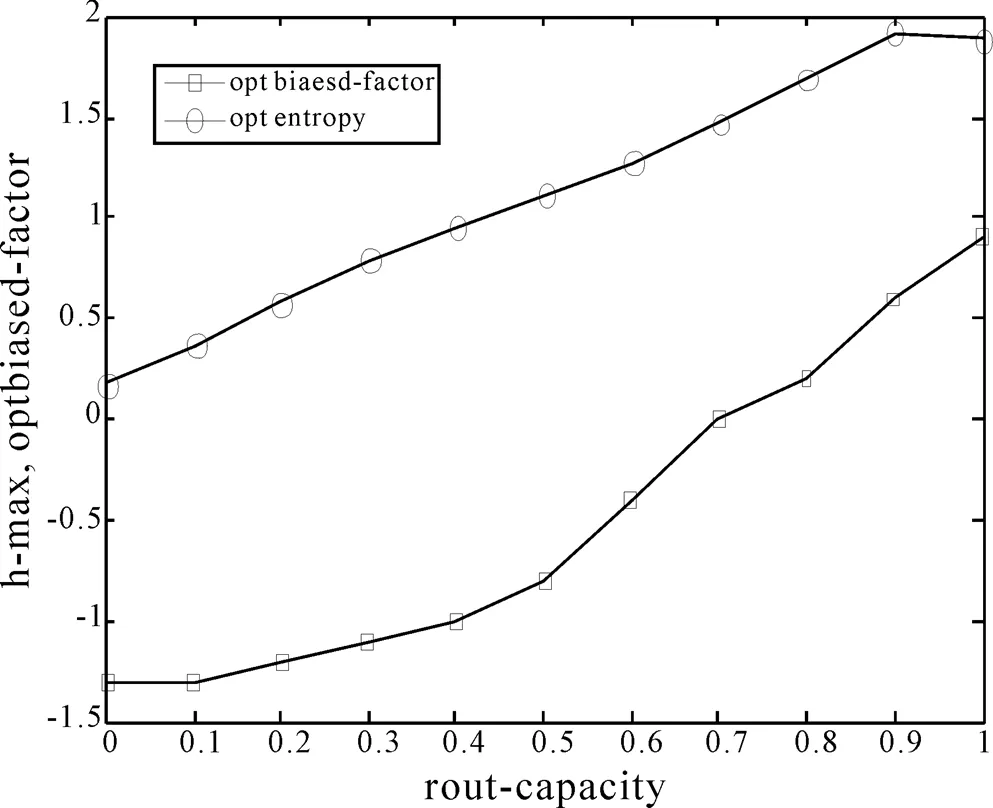
图4 不同下的熵率
4 结语
最大熵扩散过程让网络上信息粒子的行为规律具有最大复杂性和最强鲁棒性,使得信息粒子承载的关键信息难以被截取和预测;另一方面,它是网络分发信息最具效率的方法,因为最大熵过程允许信息粒子最大范围传输、关键信息高效率传播,由此使之对随机攻击具有很强的抗性. 基于这种考虑,熵或者说最大熵在信息传输系统和复杂网络的一些问题和现象中扮演着关键角色. 因此,对熵的研究将加深对复杂网络上信息传输过程的理解,并对之优化以到达最优的效果.
本文中仅得到的是数值模拟结果,希望能在理论上给出这些规律的统一描述,得到最优策率的解析表达式. 此外,本文关注的是给定网络结构下扩散动力学过程的优化问题,如何对给定的传输规则和传输能力,设计最优网络拓扑,使得系统效率达到最优也是一个亟待解决的课题.
[1] 周 漩, 张凤鸣, 惠晓滨, 等. 基于熵的复杂有向网络异质性度量方法[J]. 系统工程, 2011(8): 123-126.
[2] 王宏健, 方国兴. 仓库容量有限条件下的随机存储模型[J]. 福州大学学报: 自然科学版, 2005(6): 711-714.
[3] WALTERS PETER. An Introduction to Ergodic Theory [M]. New York: Springer-Verlag, 2000.
[4] 汪小帆, 李 翔, 陈关荣. 复杂网络理论及其应用[M]. 北京: 清华大学出版社, 2006.
[5] LOVASZ L. Random walks on graphs: A Survey[J]. Bolyai Society Mathematical Studies, 1993, 2: 1-46.
[6] 龚光鲁, 钱敏平. 应用随机过程教程及在算法和智能计算中的随机模型[M]. 北京: 清华大学出版社,2003.
[7] TANG SHAOTING, JIANG XIN, PEI SEN, et al. Highly nonlinear complexity of interaction dynamics in scale-free networks[J]. International Journal of Modern Physics C, 2011(3): 47-48.
[8] TANG SHAOTING, JIANG XIN, MA LILI, et al. On routing strategy with finite-capacity effect on scale-free networks[J]. Canadian Journal of Physics, 2010, 88(2): 139-147.
Analysis of Entropy into Finite Volume Model’s Scale-free Network Diffusion
LONG Yaohui
(Xiangyang Vocational and Technical College, Biological Engineering School, Xiangyang 441000, China)
Taking advantage of entropy to explore a kind of network interaction mechanics process, the network diffusion’s system complexity of finite volume model, to discuss the influence which the two key factors, local topology and routing capacity have on its complexity, to determine the optimal dynamics process’s system parameters and the efficient routing strategy, according to the principle of maximum entropy.
Finite volume model; Entropy; Routing capacity; Local topology; Bias factor
(责任编辑:饶 超)
O142
A
2095-4476(2015)02-0009-04
2014-06-12
龙耀辉(1982— ), 女, 湖北襄阳人, 襄阳职业技术学院生物工程学院讲师.

