噪声和捕捞对捕食生态系统稳定性的影响*

董庆国 宁丽娟

（陕西师范大学，数学与信息科学学院，西安 710062）

噪声和捕捞对捕食生态系统稳定性的影响*

董庆国 宁丽娟†

（陕西师范大学，数学与信息科学学院，西安 710062）

讨论了在色噪声激励下，具有独立常数率捕捞和庇护所效应的捕食生态系统的稳定性问题.在弱扰动假设下应用Stratonovich-Khasminskii随机平均原理分别得到了两个物种的稳态概率密度，并研究了捕捞强度E1，色噪声强度Kii，谱宽和噪声相关时间对两个物种的稳态概率密度的影响.Monte-Carlo模拟验证理论求解的合理性.研究表明：1）随着捕捞活动的增大，随机因素对生态系统的影响逐渐减弱；2）噪声强度越大，生态系统越不稳定；3）随机激励的谱带越宽，生态系统越稳定；4）随机激励的相关时间越小，生态系统越稳定.

色噪声，常数率捕捞，随机平均方法，稳态概率密度

引言

经典的Lotka-Volterra模型奠定了利用数学建模方法来分析种间关系的理论基础［1，2］.学者们对此模型进行了研究并提出了许多改进［3-7］，例如，考虑了种群间的自竞争，被捕食者依赖型Holling I-III功能反应［5］，比率依赖型功能反应［6］，庇护所效应［7］等.以上模型可以描述不同类型的确定性被捕食—捕食生态系统模型.一般地，由于环境中存在众多的不确定因素，随机模型比确定性模型更能准确表达生态系统的状态.可以对随机生态系统模型分析的途径和方法有信息熵［8］，广义图胞映射法［9］，本征值和本征矢理论（对单种群Logistic模型）［10］，路径积分法等.2004年，Cai和Lin利用随机平均法研究了在白噪声扰动下的捕食生态模型，得到了系统中两物种的稳态概率密度［11］.2013年，Qi等进一步建立了受色噪声扰动的含食物过剩和捕食者饱和的统一捕食类型的生态系统模型，并利用随机平均法得到了该统一模型中两物种的稳态概率密度［12］.

以上研究的模型中忽略了人类活动对模型的影响.事实上，研究人类活动对生态系统稳定性的影响具有重要的生态和经济价值.2006年，Kar研究了具有庇护所效应的食饵—捕食者捕捞模型，发现捕捞活动不仅可以破坏系统的周期行为，还可以控制系统的最终性态［13］.2010年，Lv等建立了在外界捕获下水生浮游植物和浮游动物构成的被捕食—捕食模型，并对其稳定性和最优捕获策略进行了研究，发现外界捕获可以导致种群灭绝，合理的捕获可以维持种群数量的稳定［14］.然而，在人类捕捞活动下的生态系统的随机模型的研究甚少.

综上所述，本文对色噪声激励下，具有独立常数率捕捞和庇护所效应的随机生态系统模型进行了研究.为了更好的描述捕捞活动对生态系统的影响，讨论了被捕食者的捕捞强度E1变化时，整个模型的性态变化.首先，研究了确定性生态系统的稳定性态，并得到了捕捞强度E1（0＜E1＜z/q1）的两个阈值e1和e2.其次，将随机模型转化为Itô随机微分方程，并在e1＜E1＜e2区间内应用随机平均法，从理论上推导了随机系统中两物种的稳态概率密度.然后，利用低通滤过过程来模拟环境中的噪声，并对真实环境中的噪声谱密度进行分析.最后，通过数值模拟，具体分析了人类捕捞和随机环境对两物种的稳态概率密度的影响，并利用Monte-Carlo模拟来验证理论分析的准确性.

1　确定性模型研究

1.1经典Lotka-Volterra模型

描述物种间相互作用的Lotka-Volterra模型［1-2］如下：

其中，x，y分别代表被捕食者和捕食者的种群数量；a，b，c和f为正常数：a代表被捕食者自然生长率（出生率），c代表捕食者自然死亡率，b和f分别代表捕食者捕食率和食物转化效率.（1）式是一保守系统，有一个不稳定平衡点（0，0），一个稳定的非渐近平衡点（c/f，a/b）.具有如下形式的首次积分［15］

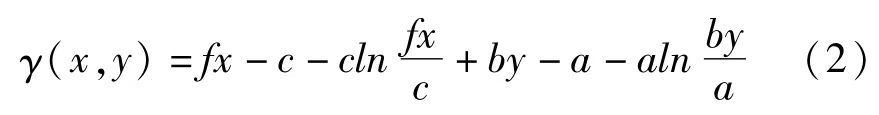
其中γ（x，y）=0对应正平衡点（c/f，a/b），且对于γ（x，y）=R（R≥0），正数x＞0，y＞0，即γ（x，y）=R描述了动力系统中两物种的周期轨道.相应轨道的周期定义为

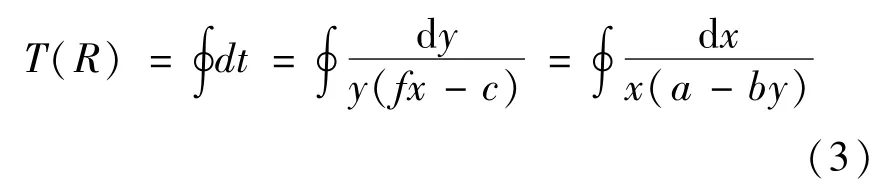
其环路积分定义在由（2）式确定的周期轨道上.

1.2具有独立常数率捕捞的生态系统模型

包含人类对被捕食者和捕食者独立常数率捕捞，被捕食者具有庇护所的捕食生态系统的确定性模型可以表示为：

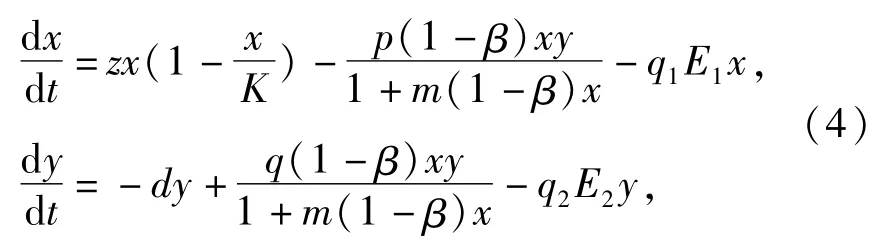
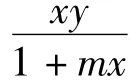
由动力系统局部稳定性判定条件，得到关于对被捕食者捕捞强度E1的两个阀值，记为e1，e2，其值为

根据极限环存在的条件［17］，当0＜E1＜e1时，系统（4）存在一个极限环；当e1＜E1＜e2时，P2是渐近稳定点；当e2＜E1＜z/q1时，P1是渐近稳定点.

表1　正平衡点P2（）的部分值（e1＜E1＜e2）Table 1 The partially value of P2（x～，y～）（e1＜E1＜e2）

表1　正平衡点P2（）的部分值（e1＜E1＜e2）Table 1 The partially value of P2（x～，y～）（e1＜E1＜e2）

E12468 P2（143.3，57.80）（143.3，45.15）（143.3，32.50）（143.3，19.84）

图1　不同E1取值下系统（4）的轨道：（a）E1=4；（b）E1=6.Fig.1 Trajectories of the system（4）with two different E1values：（a）E1=4 and（b）E1=6.

2　随机生态系统模型研究

2.1建立具有独立常数率捕捞的随机生态系统模型

环境中存在的各种不确定性因素，会对食饵出生率和捕食者死亡率产生影响.本文建立色噪声激励下的随机生态系统模型：

其中，X，Y分别代表被捕食者和捕食者的种群数量；ξi（t）（i=1，2）是相互独立的平稳色噪声，分别作用于被捕食者自然增长率z（忽略色噪声对被捕食者间竞争的影响）和捕食者自然死亡率d.其均值为零，相关函数为：

对模型（6）进行如下变换：

根据文献［18］，对于一般的随机模型：

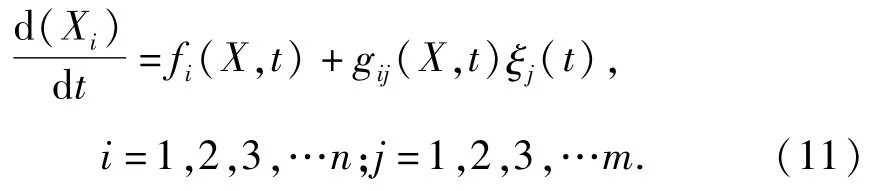
其中，fi（X，t）和gij（X，t）是关于X和时间t的函数，ξj（t）是零均值的随机激励.若ξj（t）的相关时间远小于随机过程Xi的观察时间间隔（数值积分步长）Δt，合理的选取Δt，随机过程Xi能够近似为一个Itô随机微分方程，其漂移系数aj（X，t），扩散系数bik（X，t）为：

Cjs（τ）为ξj（t）和ξs（t）的相关函数.对于相互独立的随机激励，即有Cjs（τ）=Csj（τ）=0，（j≠s）.

将（11）～（13）式应用到（9）式，可以转化为Itô随机微分方程：

其中，Kjj如（13）式定义，即近似为噪声强度. B1（t）和B2（t）为两个独立单位Wiener（维纳）过程.

2.2稳态概率密度研究

为了获得随机捕食生态系统中两物种的稳态概率密度，结合实验所得数据及（8），（10）式，对（14）式作如下说明：1）被捕食者环境容纳量参数K远大于被捕食者自然增长率参数z，故s是小量；2）当e1＜E1＜e2时，利用四阶Runge-Kutta算法计算（14）式得到G1（X，Y），G2（X，Y）均相对参数a，b，c和f是小量；3）合理假设系统受到的随机扰动ξi（t）（i=1，2）的噪声强度是小量.

定义相应于（2）式的随机过程R（t）：

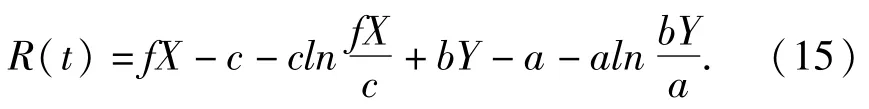
利用Itô公式及（14）式可得到关于R（t）的Itô随机微分方程：

由以上说明可知，（16）式右边是小量，即R（t）是一个慢变过程，而系统（14）可以作为保守系统（1）受扰动后产生的新系统.

根据Stratonovich-Khasminskii随机平均原理，可以得到随机过程R（t）的平均Itô随机微分方程为：

其中，m（R）和σ（R）分别为漂移系数和扩散系数，可以由下式解得：

〈·〉t表示一个周期内的时间平均，T（R）如（3）式定义.结合（1），（3）式可以得到：

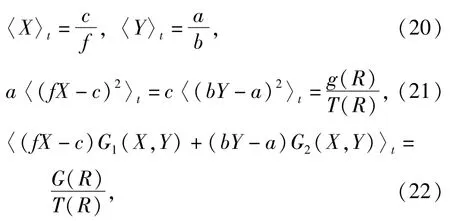
其中

将式（20）～（22）代入（18）式和（19）式得到简化后的漂移系数和扩散系数：

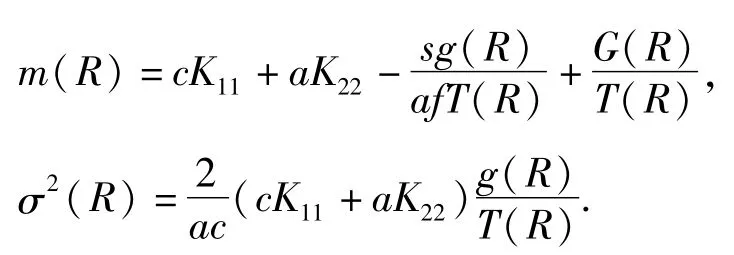
Itô随机微分方程（17）式对应的稳态概率密度满足的FPK方程为：

其中，r是随机过程R（t）的状态变量，m（r）和σ2（r）对应m（R）和σ2（R），求得（23）式对应的稳态概率密度［11］：

其中，C为归一化常数.假设当R=r时随机过程X的条件概率密度为p（x|r），则有：

由上式可得R和X的联合概率密度为：

将Y作为R和X的函数，条件概率公式和Jacobi变换得到R和X的联合概率密度p（r，x）为：

其中，C为归一化常数，从而可以得到两物种的稳态概率密度为：

p（x），p（y）的存在说明随机系统不再稳定到某个稳定点而是稳定到一定的分布.

3　数值模拟

本文采用常用的低通滤过过程产生的色噪声模型ξi（t）来模拟随机环境.低通滤过过程由下列一阶线性微分方程产生：

其中，W1（t），W2（t）是独立的高斯白噪声，其强度分别为D1（t），D2（t），可以描述色噪声ξi（t）的相关时间.ξi（t）的谱密度Φi（ω）和相关函数Cii（τ）为：

图2　αi取不同值时低通滤过过程的谱密度曲线Figure.2 Power spectral densities of the low-pass fltered processes（24）for different values of band width parameter αi

图2给出了白噪声强度为0.005，αi取不同值时低通滤过过程的谱密度曲线.可以得到，随着αi的增大，谱带变的平缓.

图3给出了参数2D1=2D2=0.01，α1=α2=2，其余参数取值如（5）式定义，E1取不同值时，两种群的稳态概率密度的解析解（Analytical）和模拟（Simulation）曲线.从图中可以得到：与确定性生态系统数据表1对应，随机系统渐近稳定时，被捕食者种群数量随着E1的增大在143.3附近振动（图3（a）），捕食者种群逐渐减少（图3（b））；两种群x，y均以固定概率在系统的平衡点附近振动，当E1=2时，振动范围最大，随着E1的变大，振动明显减少，系统振动范围趋于稳定.因此，在捕捞强度较小时，随机因素不能忽略，随着捕捞强度的加大，随机因素对系统的影响减小.解析解曲线与Monte-Carlo模拟两种群密度基本一致，说明了随机平均方法的正确性.

在其余参数取值不变的前提下，图4（a）和（b）给出了E1=6，α1=α2=2，随机激励强度2Di分别取0.005，0.01，0.05时两种群的稳态概率密度（其他参数如上）.从图中可以得到，当2D1=2D2=0. 005时，系统振动范围较小，随着2Di的增大，两种群x，y振动的范围明显较少，即说明外界不确定性因素越强，生态系统越不稳定.

图3　不同E1取值下两物种的稳态概率密度.Fig.3 The stationary probability density of two species with two different E1values..

图4　不同2Di取值下两物种的稳态概率密度.Fig.4 The stationary probability density of two species with two different 2Divalues.

图5　不同αi取值下两物种的稳态概率密度.Fig.5 The stationary probability density of two species with two different αivalues

图5（a）和（b）给出了在其余参数取值不变，2D1=2D2=0.01，E1=6，随机激励谱带宽度αi分别取1，2，3时两种群的稳态概率密度.从图中可以得到，随着αi的增大，系统振动范围减少，即可以得到，噪声谱带越宽，生态系统越稳定；另即噪声的相关时间越小，生态系统越稳定.

4　结 论

本文研究了被捕食者和捕食者具有独立常数率捕捞，被捕食者常数比例进入庇护所的捕食生态系统模型，主要分析了被捕食者捕捞强度E1在区间（e1，e2）内系统的动力学行为；建立了在更加接近实际环境的色噪声激励下的随机生态模型，并将随机模型通过近似手段转化为Itô随机微分方程，在合理假设下，利用随机平均原理得到两物种的稳态概率密度的理论解；运用Monte-Carlo模拟验证了整个理论的正确性.对两物种稳态概率密度的研究发现：捕捞活动较小时，环境因素对系统影响较大.随着捕捞活动的加大，随机因素影响逐渐减少，捕捞活动主要影响系统的稳态.噪声强度越大，随机因素对系统影响越大.噪声相关时间越小，随机因素对系统影响越小.另外，本文的模型研究捕食者捕捞强度E2不变时，被捕食者捕捞强度E1对系统的影响，对于研究E1不变，E2对系统影响的方法以及结果类似.本文所有结果与自然规律一致，可以有效地解释并指导生产实践.

本文的研究建立在具有常数率捕捞和常数比例被捕食者进入庇护所的确定性模型的基础上，并且限制在了（e1，e2）之间，对于其他类型的捕捞活动，庇护所效应模型，以及在随机激励下（0，e1），（e2，z/q1）范围内系统的运动性态及其方法，还有待研究.

1 Lotka A J.Element of Physical Biology.Baltimore：Williams and Wilkins Press，1925

2 Volterra V.Varizaioni e fluttuazioni del numero d’individui in specie d’animani conviventi.Mem Acad Lincei，1926，2：31～113

3 王洪礼，许佳，郭龙等.海洋赤潮藻类的生态动力学稳定性研究.动力学与控制学报，2005，3（2）：40～43（Wang H L，Xu J，Guo L，et al.Research of red tide in ocean on dynamical stability.Journal of Dynamics and Control，2005，3（2）：40～43（in Chinese））

4 Saha T，Bandyopadhyay M.Dynamical analysis of toxin producing Phytoplankton-Zooplankton interactions.Nonlinear Analysis：Real World Applications，2009，10：314～332

5 Holling C S.Some characteristics of simple types of predation and parasitism.The Canadian Entomologist，1959，91（7）：385～398

6 Akçakaya H R，Arditi R，Ginzburg L R.Ratio-dependent predation：an abstraction that works.Ecology，1995，76（3）：995～1004

7 Kar T K.Stability analysis of a prey-predator model incorporating a prey refuge.Communications in Nonlinear Science and Numerical Simulation，2005，10（6）：681～691

8 谢文贤，蔡力，岳晓乐.两种群随机动力系统的信息熵和动力学研究.物理学报，2012，61：170509（Xie W X，Cai L，Yue X L，et al.Information entropies and dynamics in the stochastic ecosystem of two competing species.Acta Physica Sinica，2012，61：170509（in Chinese））

9 Wu Y，Zhu W Q.Stochastic analysis of a pulse-type preypredator mode.Physical Review E，2008，77（4）：041911

10 杨会会，宁丽娟.非线性漂移的Fokker-Planck方程的近似非定态解.物理学报，2013，62（18）：180501（Yang H H，Ning L J.Approximate time-dependent solution of Fokker-Planck equation with non-linear drift force.Acta Physica Sinica，2013，62（18）：180501（in Chinese））

11 Cai G Q，Lin Y K.Stochastic analysis of the Lotka-Volterra model for ecosystems.Physical Review E，2004，70：041910

12 Qi L Y，Xu W，Gao W T.Stationary response of Lotka-Volterra system with real noises.Communications in Theoretical Physics，2013，4：503～509

13 Kumar Kar T.Modelling and analysis of a harvested preypredator system incorporating a prey refuge.Journal of Computational and Applied Mathematics，2006，185（1）：19～33

14 Lv Y，Pei Y，Gao S，et al.Harvesting of a phytoplankton-zooplankton model.Nonlinear Analysis：Real World Applications，2010，11（5）：3608～3619

15 马知恩.种群生态学的数学建模与研究.合肥：安徽教育出版社，1996，43（Ma Z N.Methods of mathematics and research in population ecology.Hefei：Anhui Education Publishing House，1996，43（in Chinese））.

16 Bairagi N，Jana D.On the stability and Hopf bifurcation of a delay-induced predator-prey system with habitat complexity.Applied Mathematical Modelling，2011，35（7）：3255～3267

17 Kuang Y，Freedman H I.Uniqueness of limit cycles in Gause-type models of predator-prey systems.Mathematical Biosciences，1988，88（1）：67～84

18 Lin Y K.Some observations on the stochastic averaging method.Probabilistic Engineering Mechanics，1986，1（1）：23～27

EFFECTS OF NOISES AND HARVESTING ON THE STABILITY IN THE PREY-PREDATOR ECOSYSTEM*

Dong Qingguo Ning Lijuan†
（College of Mathematics and Information Science，Shaanxi Normal University，Xi’an 710062，China）

This paper discusses stability problem of a new stochastic predation type ecosystem with corporating a prey-refuge and independent harvesting in either species.To explore the prey-harvesting and colored noises effects on the stability of the ecosystem，with the assumption of weak disturbances，the stationary probability density functions for both species were obtained by applying the Stratonovich-Khasminskii averaging principle.The accuracy of the results obtained from theoretical method was demonstrated by those obtained from Monte Carlo simulation.Results obtained show that：1）the ecosystem with smaller harvesting is less stable when the system is disturbed by noises；2）the stronger the noise intensities are，the less stable the ecosystem will be；3）the narrower the band width is，the less stable the ecosystem will be；a narrower band width leads to a less stable system；4）a smaller correlation time leads to a more stable system.

colored noise，harvesting，stochastic averaging，the stationary probability density

6 December 2013，revised 7 January 2014.

E-mail：ninglijuan@snnu.edu.cn

10.6052/1672-6553-2014-033

2013-12-06收到第1稿，2014-01-07收到修改稿.

*国家自然科学基金资助项目（11202120和61273311）

E-mail：ninglijuan@snnu.edu.cn

*The project supported by the National Natural Science Foundation of China（11202120 and 61273311）.