地震作用下非弹性地基桩的3次超谐波共振*

吕建根韩强王荣辉

（1.仲恺农业工程学院城市建设学院，广州 510225）（2.华南理工大学土木与交通学院，广州 510641）

地震作用下非弹性地基桩的3次超谐波共振*

吕建根1†韩强2王荣辉2

（1.仲恺农业工程学院城市建设学院，广州 510225）（2.华南理工大学土木与交通学院，广州 510641）

研究了地震作用下非线性地基中桩基的3次超谐波共振问题.从地基桩中抽象出力学模型，考虑地基的非线性因素，运用Hamilton变分原理建立了桩基的非线性控制方程.利用Galerkin方法离散上述方程，基于多尺度摄动法研究了地震作用下非线性地基中桩的3次超谐波共振问题.以某嵌岩圆形桩为例，研究了地基土层厚度、剪切波速度及频率比对地震力的影响，数值模拟了非线性地基桩的3次超谐波共振响应，探讨了地震力、地基弹性及非弹性系数对超谐波幅频响应的影响，最后研究桩基产生3次超谐波共振时的时间历程曲线.结果表明，当地震波频率约等于桩基固有频率的1/3时，容易激发桩的3次超谐波共振响应；桩基的3次超谐波共振响应随着地震力、非弹性系数的增大而变得更加显著，随着弹性系数的增大而逐渐变小.

桩，地震力，非线性地基，3次超谐波

引言

桩基础由于其具有承载能力大、沉降量小及稳定性好等优点而广泛应用于土木工程领域中，同时，桩基础也能适用于各种地质环境和各种荷载情况，在抗震结构设计中也是优先采用的基础型式 ，因此桩基的动力性能的研究成为地震工程界和土木工程界一个重要的研究热点［1-4］.

与桩基的静力学理论相比，桩基的动力学理论研究开展较晚，大约起步于二十世纪七十年代，目前针对桩基的动力学研究国内外开展了不少工作，九十年代前的工作主要总结在Novak［5］的综述报告中，系统介绍了单桩和群桩在地震载荷作用下线性和非线性动力学的一些理论、计算方法以及一些定性的结论，并比较了各种理论的优缺点.1987年，Mizuno［6］综述了日本地震过程中桩基的破环形式，如液化、振动及运动等，这些破坏形式在其他地区的地震中都能观察到.刘宗贤等［7］得到了地基波动影响下端承桩的横向地震反应解析解.2005年，胡和程［8］建立桩-土相互作用的数学模型，在频域内研究了水平振动下桩基的非线性动力学特性，研究了多种参数对桩基动力学特性的影响.2014年，吕建根［9］研究了地震作用下桩基的1/3次亚谐波共振问题，分析了频率比、剪切波速度及土层厚度等参数对地震惯性力和亚谐波共振幅频响应的影响.除此之外，还有许多国内外学者对桩基的动力学问题进行了深入的研究，这里不再一一赘述.

本文基于Hamilton变分原理推导了地震作用下非线性桩基的非线性控制方程，采用Galerkin离散方法，研究了桩的3次超谐波共振问题，分析了系统参数对地震力的影响，得到了超谐波共振响应，探讨了各项参数对超谐波幅频响应的影响，获得了桩出现3次超谐波共振时的时间历程曲线，其研究结果对桩基的动力学设计具有参考价值.

1　振动方程

如图1所示桩基础，地基土层厚度为H，桩基的密度为ρ，桩的横截面面积为A，抗弯刚度为EI，c为粘性阻尼系数，桩基相对于地面的位移为w（z，t），地基的线弹性系数为k1，地基的非线性弹性系数为k3，外荷载为p（z，t），运用Hamilton变分原理可以得到如下形式的桩基非线性控制方程：

图1　桩基的分析模型Fig.1 The model of pile foundation

对方程（1）进行一阶Galerkin离散，设w（z，t）=U（z）X（t）代入上式中

其中：

经过上面推导后，地震作用下非线性弹性地基桩的振动控制方程如下：

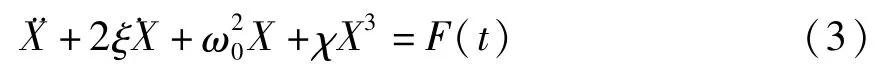
地震作用F（t）通常随时间不规则变化，但对于含无限地基的开放系统，任意地震作用可展开为简谐波的叠加，均匀地基中地震荷载作用F（t）可用下式表达［10］.

其中：

ω1=Vs，Vs为地基的剪切波速度.H为桩长及地基土层厚度，α表示水平地震影响系数，g表示当地重力加速度，v为地震波频率.从上式可以看出，作用于桩基上的地震荷载既包含地震时基岩产生的惯性力，又包含土层运动产生的惯性力，该惯性力与地基的性质相关.

2　多尺度法求解

为了摄动分析方便，引入小参数ε，将2ξ表示为2εξ，将非线性项的系数χ表示为εχ利用多尺度方法［11］对方程（3）求解，设一次近似解的形式如下：

其中T0=t，T0=εt.将（5）代入（3）式，可以得到

零阶近似方程（6a）的解为

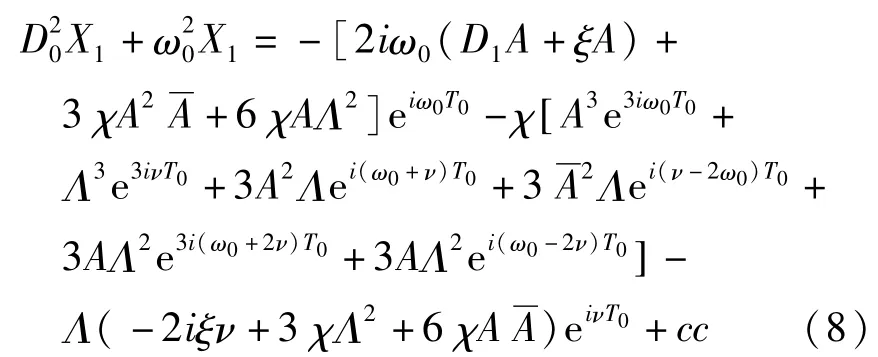
上式中可以看出，不仅存在eiω0T0项可以引起久期项，而且还存在含e3iνT0项.当ω0=3ν时，也能产生久期项，即桩基可产生3次超谐波共振.为了描述ω0和3ν的差别，引入调谐参数σ，即3ν=ω0+εσ，代入方程（8）中，消除久期项，得到

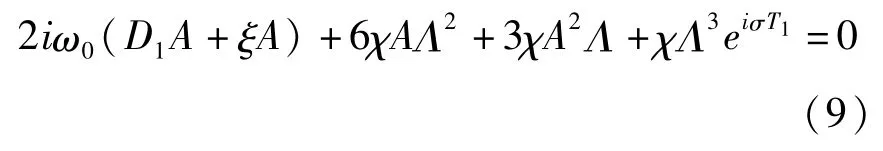
将复数形式的A函数对t求导，其中的D0A= 0，D1A由方程（9）确定，代入方程（9）中，分离实部和虚部，得到关于a和β的一阶常微分方程组：

其中γ=σT1-β.方程组（10）的非平凡解对应桩基的稳态周期振动，即˙a=˙γ=0，消除γ，可以得到桩基3次超谐波稳态周期振动的幅频响应方程

从上式中可以看出，当ω0≈3ν时，即使存在阻尼，也存在满足方程（12）的非零解，从而表明桩基存在3次超谐波共振现象.

3　桩基实例分析

以嵌岩桩为例，桩底处满足固定端的边界条件，对于嵌固于承台或地基梁中的桩头，其转角为零，并由等效剪力为零的边界条件可知，其横向振型函数U（z）可采取如下形式［12］：

圆形桩的参数：桩长H=10m，直径D=1.2m，材料密度ρ=2.4×109kg/m3；弹性模量E=2.1× 1010Pa；阻尼系数ξ=0.01；地基的参数：剪切波速度Vs=200m/s，线性弹性系数k1=8×106N/m2，非线性弹性系数k3=8×106N/m4；地震参数：水平地震影响系数α=0.5或0.15.

图2～图4显示了各项参数对地震力的影响，从图2可以看出，地震力随着土层厚度的增加而逐渐增大，同时表明，随着频率比ν/ω0的增大，地震力增大速率越快；图3表明，地震力随着频率比ν/ω0的增大而增大，同时显示，随着剪切波速度的增大，地震力增加速度变慢；从图4中可以看出，地震力随着剪切波速度的增大逐渐变小，大约在剪切波速度等于100m/s时，影响基本可以忽略.

图2　地震力F0与地基土层厚度H的关系Fig.2 The relationship between seismic forces and soil thickness

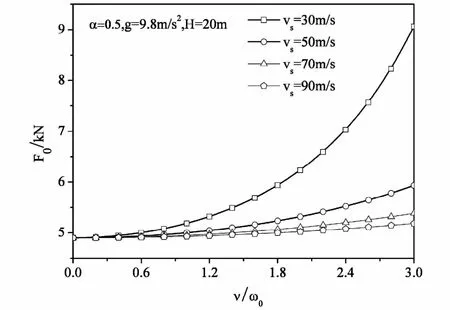
图3　地震力F0与频率比ν/ω0的关系Fig.3 The relationship between seismic forces and frequency ratio

图4　地震力F0与剪切波速度Vs的关系Fig.4 The relationship between seismic forces and shear wave velocity

图5　地震力F0对超谐波幅频曲线的影响Fig.5 Effect of seismic force on the frequency response curves

图5～图7显示了地震力、弹性及非弹性系数对超谐波幅频响应曲线的影响，从图5中可以看出，随着地震力的逐渐增大，桩的3次超谐波共振响应逐渐增大，共振频域变宽，出现3次超谐波共振的可能性增大，非线性性质逐渐明显；图6表明，随着弹性系数的增大，桩的3次超谐波共振响应逐渐减小，非线性性质变弱，共振频域变窄；从图7可以看出，随着非线性弹性系数的增大，桩的非线性更加明显，3次超谐波响应也逐渐增大，共振频域变宽.图8显示了桩出现3次超谐波共振时的时间历程曲线，从图中可以看出，桩的最大位移达到6cm.

图6　弹性系数k1对超谐波幅频曲线的影响Fig.6 Effect of elastic coefficient on the frequency response curves

图7　非弹性系数k3对超谐波幅频曲线的影响Fig.7 Effect of elastic coefficient on the frequency response curves

图8　桩基时间历程曲线Fig.8 The time history of pile foundation

4　结论

本文针对地震作用下非线性弹性地基中桩的3次超谐波共振问题开展研究，基于Hamilton变分原理推导了非线性地基中桩的非线性控制方程，运用Galerkin方法离散时间和空间，利用多尺度摄动法获得了桩3次超谐波共振时的幅频响应曲线，基于工程实例，探讨了各项参数对地震力大小的影响，研究地震力、弹性及非弹性系数对3次超谐波共振的影响，最后得到了桩3次超谐波共振的时间历程曲线，结果表明：

（1）当地震波频率约等于桩基固有频率的1/3时，容易激发桩的3次超谐波共振响应，其共振幅值较大；

（2）桩基的3次超谐波共振响应随着地震力、非线性弹性系数的增大而变得更加显著，随着弹性系数的增大而逐渐变小.

1 黄雨，舒翔，叶为民等.桩基础抗震研究现状.工业建筑，2002，32，50～52（Huang Y，Shu X，Ye W M，etc.Recent studies on seismic resistance of pile foundation.Industrial Construction，2002，32：50～52（in Chinese））

2 Nogami T，Novak M.Resistance of soil to a horizontal vibrating pile.Earthquake Engineering and Structural Dynamies，1977，5：249～261

3 花羽超，朱媛媛，程昌钧.非线性桩基的动力响应分析.动力学与控制学报，2007，5（3）：238～243（Hua Y C，Zhu Y Y，Cheng C J.Dynamic response analysis of nonlinear piles.Journal of Dynamics and Control，2007，5（3）：238～243（in Chinese））

4 任九生，程昌钧.地基波动影响下非线性粘弹性桩的混沌运动分析.动力学与控制学报，2005，3（1）：29～33（Ren J S，Cheng C J.Chaotic motion analysis in piles of nonlinear viscoelastic materials considering the motion of ground soil.Journal of Dynamics and Control，2005，3（1）：29～33（in Chinese））

5 Novak，M.Piles under dynamic loads.In：Proceedings of Second International Conference on Recent Advances in Geotechnical Earthquake Engineering and soil Dynamic.St Louis：University of Missouri Press，1991：2433～2456

6 Mizuno H.Pile damage during earthquakes in Japan.Proceeding of the session on dynamic response of pile damage.Atlantic City：The American Society of Civil Engineers，1987：53～78

7 刘宗贤，李玉亭，傅文彬.端承桩在层状地基波动与辐射阻尼影响下的横向地震反应分析.东北地震研究，1998，14（2）：43～48（Liu Z X，Li Y T，Fu W B.Transverse earthquake response of pile under the motion of layered soils and pile viscosity.Seismological Research of Northeast China，1998，14（2）：43～48（in Chinese））

8 胡育佳，程昌钧.水平振动下桩基的非线性动力学特性.应用数学和力学，2005，26（6）：645～652（Hu Y J，Cheng C J.Characterities of piles under horizontal vibration.Applied Mathematics and Mechanics，2005，26（6）：700～708（in Chinese））

9 吕建根，邱剑辉.地震作用下桩基的1/3次亚谐波共振分析.科学技术与工程，2014，14（5）：192～196（Lv J G，Qiu J H.1/3 sub-harmonic response analysis of pile foundation under earthquake action.Science Technology and Engineering，2014，14（5）：192～196（in Chinese））

10 房营光.岩土介质与结构动力相互作用理论及其应用.北京.科学出版社，2005：261～274（Fang Y G.The dynamic interaction theory and its applications of soil medium and structure.Beijing：Science Press，2005：261～274（in Chinese））

11 Nayfeh A H，Mook D T.Nonlinear oscillations.New York：Wiley，1979：174～175

12 任九生，程昌钧.粘弹性桩的混沌运动分析.力学季刊，2004，25（3）：349～354（Ren J S，Cheng C J.Analysis of chaotic motion on piles with nonlinear viscoelastic Materials.Chinese Quarterly of Mechanics，2004，25（3）：349～354（in Chinese））

SUPER-HARMONIC RESONANCE OF PILE FOUNDATION UNDER EARTHQUAKE ACTION*

Lv Jiangen1†Han Qiang2Wang Ronghui2
（1.School of Urban construction，Zhongkai University of Agriculture and Engineering，Guangzhou 510225，China）
（2.School of Civil Engineering and Transportation，South China University of Technology，Guangzhou 510641，China）

The 3 super-harmonic response of pile foundation under earthquake action was investigated.Based on Hamilton Variational Principle，the nonlinear equations of motion on pile under earthquake action were established.Then the Galerkin method was used to discrete the governing equation.The 3 super-harmonic response of pile was studied by using the multi-scale method.The effects of the soil thickness，the shear wave velocity and the frequency ratio on the seismic force were studied，and the effects of the seismic force，elasticity coefficient and inelasticity coefficient on the frequency-response curves were studied.The results are as follows：the 3 superharmonic resonance may be excited when the earthquake frequency and the pile frequency are in an almost 1：3 ratio，the 3 super-harmonic responses of pile increase with the increase of seismic force and non-elastic coefficient，but decrease with the increase of elastic coefficient.

pile，earthquake action，nonlinear foundation，3rd super harmonic resonance

5 August 2014，revised 8 September 2014.

E-mail：lvjiangen77@163.com

10.6052/1672-6553-2014-074

2014-08-05收到第1稿，2014-09-08收到修改稿.

*国家自然科学基金资助项目（51378220）

E-mail：lvjiangen77@163.com

*The project supported by the National Natural Science Foundation of China（51378220）