基于浅水波理论液体晃动初值问题的数值模拟
薛伟顺 熊渊博
(四川大学建筑与环境学院,成都 610065)
基于浅水波理论液体晃动初值问题的数值模拟
薛伟顺 熊渊博†
(四川大学建筑与环境学院,成都 610065)
针对日益受到关注的液体晃动问题,提出了一种基于浅水波理论的研究方案.该方案采用浅水波理论而非势流理论导出系统控制方程,并通过哈密顿体系表达;利用中心有限差分法和Stormer-Verlet算法进行空间和时间离散;模拟了不同初值条件下的液体晃动情况并对比分析了影响系统非线性响应的主要因素.结果表明,基于浅水波理论能有效解决液体晃动问题;与Euler格式对比,Stormer-Verlet算法精度较高;除共振外对于系统非线性响应的影响容器初始位移比初始速度更显著;非共振情况一定条件下,充液容器运动过程中液体晃动能起到阻尼作用.
液体晃动,浅水波理论,初值问题,数值模拟,非线性
引言
液体晃动问题普遍存在于工业流水线、航天航空、能源动力、原油储运等众多工程领域,且日益得到工程界和学术界的关注.尤其近些年来,随着航空、船舶等领域的快速发展,舱内液体晃动问题引起了人们极大地关注[1-2].当容器部分充液时,液体在外部激励下会晃动起来,可能对结构安全造成严重的危害.因此,对不同激励形式下充液系统响应进行研究有着非常重要的工程应用价值.
在液体晃动的描述和液体晃动的物理特性等方面,国内外许多专家学者开展了大量的研究.卢军等[3]基于势流理论研究了平放圆柱形贮箱内任意充液比液体晃动问题;J.H.Jung等[4]采用VOF方法对液体晃动问题进行了数值计算;李裕龙等[5]模拟计算了舱内液体的非线性晃荡并建立了波浪中载液船舶耦合运动方程;R.Sygulski[6]假设流体为无黏、不可压缩、微幅晃动的理想流体,采用边界元方法研究了三维液体的晃动问题;刘富等[7]采用SPH方法对棱形液舱不同充液比所对应的舱内液体晃动进行了三维数值模拟;欧阳林辉等[8]利用有限体积法研究液体晃动行为,对二维和三维矩形储液容器液体晃动进行了分析;孙丽娜等[9]对罐式集装箱液体晃动过程进行了数值模拟研究;李文盛等[10]基于非线性波动理论模型,研究了储液容器内液体晃动的动力学响应问题.然而在以往的液体晃动问题的研究中,更多的是以势流理论为基础,导出系统的控制方程,考虑外部激励频率与容器一阶固有频率相近或相等时的液体晃动问题[12],而对诸如容器初始位移、容器初始速度等更一般的初值条件对液体非线性响应的影响分析还不多.
为了提出有效的数值方案,并比较分析影响液体晃动非线性响应的不同初始条件,从而为以后进一步研究液体晃动控制问题提供可靠参考.本文尝试以浅水波理论为基础,导出系统的控制方程,进而得到完整的数值方案.在此基础上,对系统在不同初始条件下的非线性响应做了数值仿真对比试验.通过将该方案与成熟的数值方案进行对比,证明了该方案能够精确稳定的对浅水晃动与容器平动的动态耦合问题进行计算,并且具有较高的精度.
1 系统控制方程
容器水平运动,令q(t)表示空间坐标(X,Y)下容器的水平位移,k为弹性常数,h0为静水位,L为容器水平长度,(x,y)为随体坐标系,则运动系统如图1所示.

图1 部分充液容器的运动原理图Fig.1 Schematic of a moving vehicle partially filled with fluid
容器水平运动控制方程[11]

式中,ρ为液体密度,h(x,t)为液体高度,U(x,t)为液体水平表面速度,mf为液体质量,mv为容器质量,˙q为容器水平速度.
浅水方程[13]如下
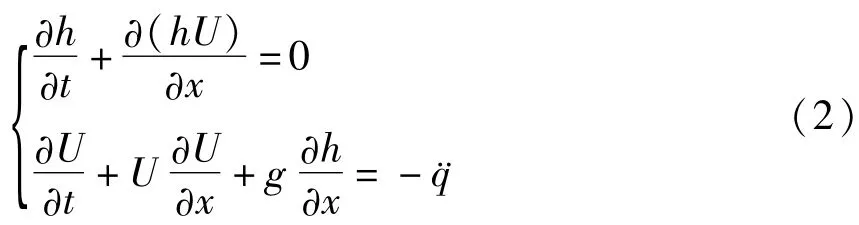
式中,g为重力加速度,¨q为容器水平加速度.
联合(1)和(2)得到刚性容器水平运动导致液体晃动的系统动态耦合控制方程.则哈密顿体系下系统控制方程如下
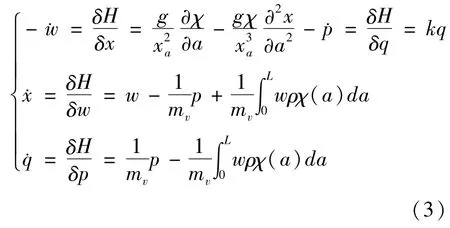

2 液体晃动问题的数值分析
2.1空间离散
离散参考空间如下

令xi(t)=x(ai,t),wi(t)=w(ai,t),控制方程(3)中第一个方程等式右侧采用变分离散[14];利用梯形法则离散(3)第三个和第四个方程中的积分项.
由此得到半离散化的哈密顿形式的控制方程组如下

式中,η为梯形法则,具有广义动量p的量纲.
2.2时间离散
时间离散采用如下方案
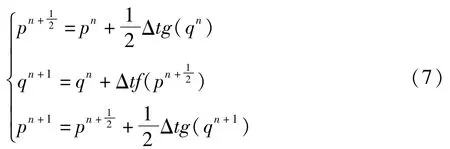
这个方案即Stormer-Verlet算法,它是显式的,并且在长时间跨度上能保持能量守恒[15].
对(6)在每个时间步n↦n+1中应用Stormer-Verlet算法,得到离散控制方程如下
式中

耦合系统的能量方程
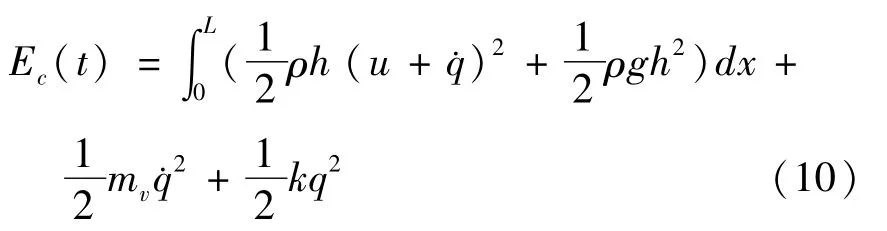
当转化为以正则变量(q,x,p,w)表示的形式时即为哈密顿方程(4).
2.3系统的数值仿真试验
取液体密度ρ=1000kg/m3,重力加速度g= 9.81 m/s2,容器水平长度L=0.525m,为满足浅水波方程水深远小于波长的适用条件,水深在0.05m~0.08m之间取值,空间步长Δa=1.05×10-4m,时间步长Δt=10-4s.


其中sj是满足方程

的有限正解,其中R是与质量有关的无量纲参数,G是与能量有关的无量纲参数.图3(a)和图4(a)分别给出系统能量误差和液面波动情况.由图3(a)可以看到采用该方案系统能量误差波动稳定并保持有界,量级保持在10-6,足够小.由图4(a)液面波动情况可以看到仿真结果出现多峰波,表现出明显的非线性符合共振对液体波动的实际影响,说明该方案是合理的.
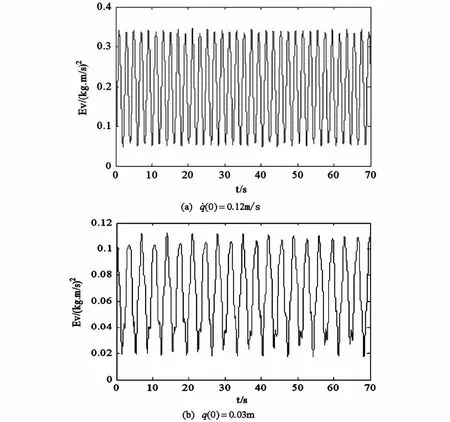
图2 能量Ev随时间t的波动图Fig.2 Energy-time curves

图3 能量误差Fig.3 Energy error
上述两种初始条件下,能量波动和液面波动都表现出了一定的非线性,但q(0)=0.03m时非线性表现更为明显,说明在相同条件下,即使容器的初始位移很小,系统也表现出明显的非线性.q(0)=0.03m时虽然液面出现明显的非线性波动,能量波动剧烈,但依然很快达到收敛,并且保持在有界范围内,计算稳定性较好.两种初始条件下能量标准误差均保持了足够小量级,保证了较高的精确度,说明数值结果是稳定可靠的.由能量误差波动曲线同样可以看出,计算很快达到稳定并能保持足够小量级,˙q(0)=0.12m/s时误差虽然出现了“漂移”,但计算表明漂移量很小并没有发生数量级的跳跃,计算结果是可靠的.表1能量标准误差再次印证了以上得出的结论,对比表中数据可以看出,相同条件下本文所采用的算法在精度上有显著提高.
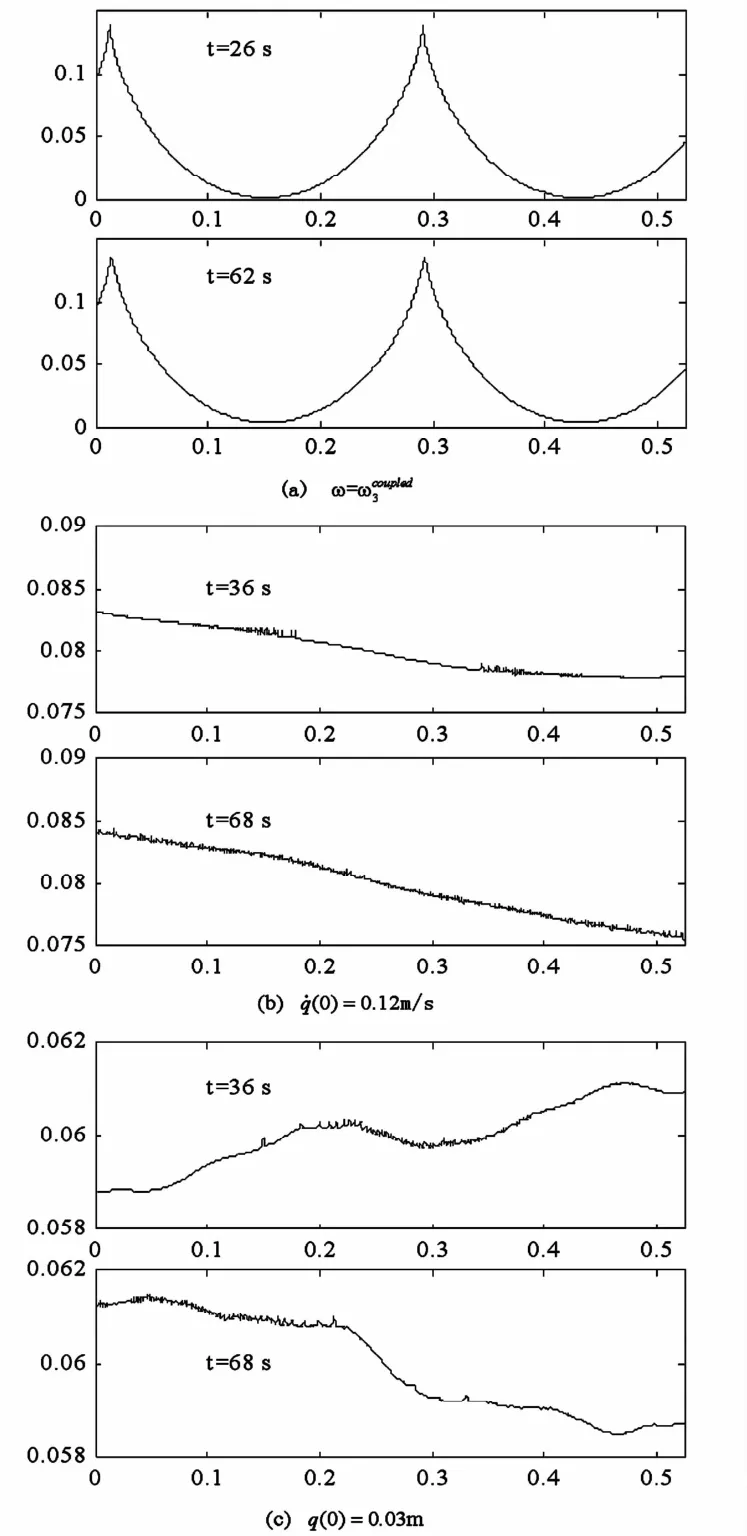
图4 随机捕捉的自由液面Fig.4 Snapshots of the free surface profile
最后考虑给液面一个初始位移,液体静止,忽略弹性力,来探究液体晃动是如何影响容器运动的.取液面初始倾角θ0=-0.5℃,规定逆时针旋转为正,自由液面的初始位置为
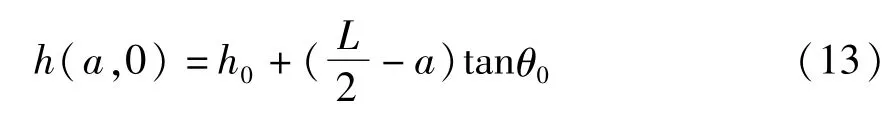
容器水平位移及其细节在图5中给出,能量波动及其误差在图6和图7中给出,能量标准误差在表1中列出.

表1 能量标准差表Table 1 Standard deviation of the energy

图5 容器的位移q(t)随时间t的变化情况及0s~5s容器的位移q(t)随时间t的变化情况Fig.5 Computed vehicle position-time curves of the container together with the corresponding curves in sub-interval of 0s~5s

图6 能量Ev随时间t的波动图Fig.6 Energy-time curve
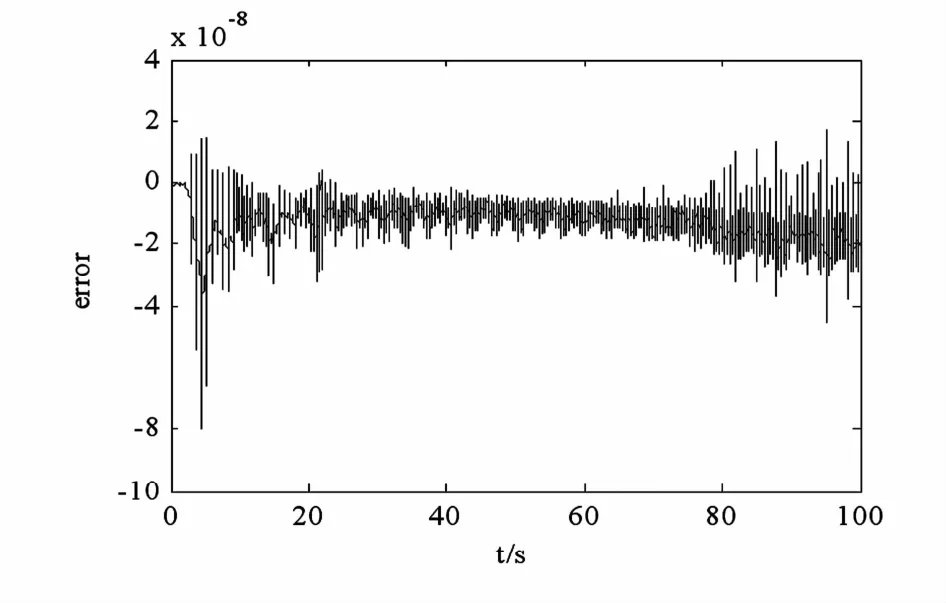
图7 能量误差Fig.7 Energy error
当k=0kg/s2时,积分q(t)表达式并代入初始条件得到
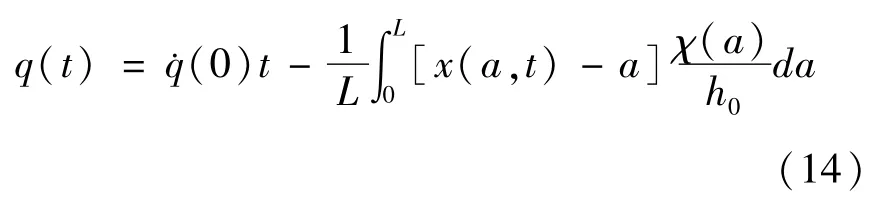
等式右端第一项是均匀位移,其中˙q(0)= 0.01m/s,这从图4中0s~100s的宏观图像中容器位移和时间基本呈线性关系得到表现,第二项令容器位移产生波动,这是由于液体质心的晃动所导致的,取一段短时间的位移进行观察,在图4中0s~5s容器位移的微观图像中可以看出曲线有一定的波动,说明液体晃动在系统运动过程中起到阻尼作用.另外,结合图5图6与表1可以看出此时能量出现不稳定波动,但依然保持有界,误差很快达到稳定并在足够小范围内波动,并且能量标准误差足够小,精度保持在10-8量级,表明算例的计算结果依然是可靠的.
3 结论
针对液体晃动问题,本文提出了基于浅水波理论,结合Stormer-Verlet算法模拟的方案.该方案采用浅水波理论导出系统的控制方程,利用中心有限差分进行空间离散结合Stormer-Verlet算法进行时间离散,得到了精确稳定的数值离散方案,通过与Euler格式对比,本文方法在计算效率相近的情况下其精度显著提高,并能够快速收敛和保持较好的稳定性.模拟结果表明,基于浅水波理论能有效地解决液体晃动问题.
利用哈密顿体系表达系统控制方程,为一般的导出简明有效的数值方案奠定了基础.首先利用共振算例验证算法精度及方案有效性,然后对初始状态分别取容器初始位移不为零和容器初始速度不为零的两种情况进行了对比讨论,得出除共振频率外,容器初始位移对液体非线性晃动的影响更为显著,在工程应用中应该引起重视.然后探究了液体晃动对刚性容器运动的影响,发现非共振情况一定条件下由于液体质心的晃动,液体在系统运动过程中能起到阻尼的作用.
本文模拟方案为进一步研究更为复杂工况条件下充液系统响应以及液体晃动控制问题奠定了基础.
1 Xue M A,Lin P Z.Numerical study of ring baffle effects on reducing violent liquid sloshing.Computers&Fluids,2011,52:116~129
2 Hasheminejad S M,Aghabeigi M.Sloshing characteristics in half-full horizontal elliptical tanks with vertical baffles. Applied Mathematical Modeling,2012,36(1):57~71
3 卢军,杨翊仁.平放圆柱体内液体晃动特性及横向受力分析.科学技术与工程,2009,9(14):3945~3949(Lu J,Yang Y R.Characteristics of liquid sloshing and transverse force analysis of horizontal liquid-filled cylindrical tank.Science Technology and Engineering,2009,9(14):3945~3949(in Chinese))
4 Jung J H,Yoon H S,Lee C Y,et al.Effect of the vertical baffle height on the liquid sloshing in a three-dimensional rectangular tank.Ocean Engineering,2012,44:79~89
5 李裕龙,朱仁传,缪国平等.波浪中载液船舶运动的时域模拟.上海交通大学学报,2012,46(3):379~384(Li Y L,Zhu R C,Miao G P,et al.Simulation of ship motions coupled with tank sloshing in time domain.Journal of Shanghai Jiaotong University,2012,46(3):379~384(in Chinese))
6 Sygulski R.Boundary element analysis of liquid sloshing in baffle tanks.Engineering Analysis with Boundary Element,2011,35(8):978~983
7 刘富,童明波,陈建平.基于SPH方法的三维液体晃动数值模拟.南京航空航天大学学报,2010,42(1):122~126(Liu F,Tong M B,Chen J P.Numerical simulation of three-dimensional liquid sloshing based on SPH method. Journal of Nanjing University of Aeronautics&Astronautics,2010,42(1):122~126(in Chinese))
8 欧阳林辉,邓晓涛,霍世慧.基于有限体积法的液体晃动数值模拟.航空制造技术,2013,19:75~79(Ouyang L H,Deng X T,Huo S H.Numerical simulation of sloshing waves based on volume of fluid method.Aeronautical Manufacturing Technology,2013,19:75~79(in Chinese))
9 孙丽娜,周国发.罐式集装箱液体晃动过程数值模拟研究.振动与冲击,2012,31(22):147~150(Sun L N,Zhou G F.Numerical simulation for liquid sloshing process of a tank truck.Journal of Vibration and Shock,2012,31(22):147~150(in Chinese))
10 李文盛,赵友清,贾善坡等.储液容器内液体晃荡的非线性动力学分析.爆炸与冲击,2014,34(1):87~92(Li W S,Zhao Y Q,Jia S P,et al.Numerical analysis on liquid sloshing in storage container by nonlinear dynamics method.Explosion and Shock Waves,2014,34(1):87~92(in Chinese))
11 宁德志,宋伟华,滕斌等.容器固有频率对液体晃荡的影响.海洋科学进展,2012,30(1):45~53(Ning D Z,Song W H,Teng B,et al.Effect of natural frequencies of container on fluid sloshing.Advances in Marine Science,2012,30(1):45~53(in Chinese))
12 Cooker M J.Water waves in a suspended container.Wave Motion,1994,20(4):358~395
13 Alemi Ardakani H,Bridges T J.Dynamic coupling between shallow-water sloshing and horizontal vehicle motion.European Journal of Applied Mathematics,2010,21(6):479~517
14 Marsden J E,West M.Discrete mechanics and variational integrators.Acta Numerica,2001,10:357~514
15 Hairer E,Lubich C,Wanner G.Geometric numerical integration illustrated by the Stormer-Verlet method.Acta Numerica,2003,12:399~450
NUMERICAL SIMULATION ON THE INITIAL VALUE PROBLEMS OF LIQUID SLOSHING BY SHALLOW WATER WAVE THEORY
Xue Weishun Xiong Yuanbo†
(College of Architecture and Environment,Sichuan University,Chengdu 610065,China)
Based on the shallow water wave theory,a research scheme was proposed for liquid sloshing problems in this paper.In this scheme,the system control equations was derived using the shallow water wave theory rather than potential flow theory,and Hamiltonian system was used to express the equations.The centered finite difference and Stormer-Verlet algorithm were then used for discrete space and time,respectively.Moreover,liquid sloshing under different initial conditions were simulated and compared to obtain the main factor that affecting the nonlinear response of the system.The simulating results indicate that shallow water wave theory can effectively solve the problem of liquid sloshing.Compared with the Eulerian scheme,the Stormer-Verlet scheme had higher accuracy,while compared with the initial velocity of the vehicle,the initial displacement had more remarkable effect on the nonlinearity response of the system.It is also found that under certain conditions,liquid sloshing acted as damping in the process of the vehicle movement.
liquid sloshing,shallow water wave theory,initial value problems,numerical simulation,nonlinearity
23 January 2015,revised 8 April 2015.
E-mail:xyuanbo@163.com
10.6052/1672-6553-2015-020
2015-01-23收到第1稿,2015-04-08收到修改稿.
E-mail:xyuanbo@163.com.

