一类不连续映射的分岔分析*
李群宏韦丽梅 卢裕木
(广西大学数学与信息科学学院,南宁 530004)
一类不连续映射的分岔分析*
李群宏†韦丽梅 卢裕木
(广西大学数学与信息科学学院,南宁 530004)
研究一类一维分段不连续映射的边界碰撞分岔问题,推导了周期n解的边界碰撞分岔曲线及fold分岔条件,通过数值仿真验证了这些条件的正确性.研究发现系统存在周期增加序列和周期叠加序列.最后,对分段不连续映射进行三参数分岔研究,揭示了系统各参数对其动力学行为的综合影响.
分段映射,边界碰撞分岔,周期叠加,周期增加
引言
一些工程和物理科学的问题在数学上可由非光滑系统表出,如碰摩转子[1]、干摩擦振子[2]、心脏模型的一种交替现象等经常表示为分段映射模型.在非光滑系统的分析中,边界碰撞分岔研究对于描述系统的动力学行为具有重要作用.许多学者对不同非光滑系统的边界碰撞分岔做了大量工作. Nusse等[3]研究了二维分段映射的边界碰撞分岔现象.此外,Nusse等[4]指出了一维分段映射在发生边界碰撞分岔后将出现周期运动转化为混沌、多带混沌以及周期增加分岔现象.Feigin等[5]对n维映射中的边界碰撞分岔的分类做了开创性的研究. Di Bernardo等[6]将该系列成果在现代分岔理论框架下对分段映射的边界碰撞分岔进行分类.Chin等[7-8]分析了二维分段映射在发生擦边碰撞后系统将出现周期增加和周期共存现象.
根据系统在边界性质的不同,可将系统分为分段光滑连续系统和分段光滑不连续系统.虽然两者都能产生边界碰撞分岔,但所得分岔性质有明显差异.对一维分段光滑连续系统,文献[9-13]研究表明系统在发生边界碰撞分岔后均产生成对的环(鞍结点型和鞍点-鞍点型),也可发生环的同宿分岔.对一维分段光滑不连续系统,文献[14-15]研究结果表明系统在发生边界碰撞分岔后不仅能产生单一的环,还伴随周期增加、周期叠加、混沌等动力学行为.以上考虑的分段映射具有如下特性:分界面一侧函数是单调增函数,另一侧函数是单调减函数,且其中一侧函数具有不动点.最近,文献[16-17]讨论了一维分段光滑不连续系统中两侧函数都为单调增函数的情况.
在文献[15]中,考虑了如下分段映射:

该模型可以用来解释一些经济现象,如技术交易与基本交易间的金融关系,“牛熊市动力学”,金融危机等.再比如,在股市交易市场中,价格的调整过程可以用简单的线性函数表示,而庄家的调节模式则用双曲线函数表示.对上述系统,文献[15]只讨论了参数范围为a>1,a<c,1<c<b的情形,研究结果表明:以上系统存在周期增加1的序列RLk和周期增加2的序列LRk,并伴随出现周期窗口与混沌相交替的现象.本文研究系统(1)在f(x)=ax+b且a>1,0<c<1,0<b<1时系统动力学行为的变化.通过理论分析与数值分析,不仅得到系统存在周期增加序列和周期叠加序列的结果,而且对三参数分岔的研究展现了系统全部参数对其动力学行为的综合影响.因此,本文是对文献[15]的进一步补充和完善.
1 系统模型
考虑如下映射:

由于分段映射(2)两边都是单调增函数,为了后面讨论的需要,要求映射(2)满足以下条件:

由(3)、(4)解得a>1,0<c<1,0<b<1.映射(2)的图像如图1所示.

图1 当a=5,b=0.2,c=0.7时分段映射T(x)的图像Fig.1 Schematic diagram of the piecewise map T(x)with a=5,b=0.2,c=0.7
分段映射(2)的不变吸引区间为
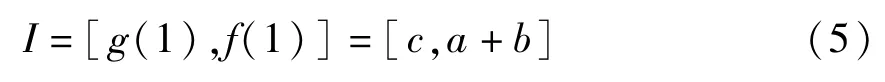
本文将在此不变吸引区间上研究映射(2)的动力学行为.
2 以b为分岔参数的边界碰撞分岔
以b为分岔参数,系统(2)的全局分岔图如图2所示.由图2可知,映射(2)存在周期增加序列和周期叠加序列.以下将通过理论分析证实数值结果的准确性.
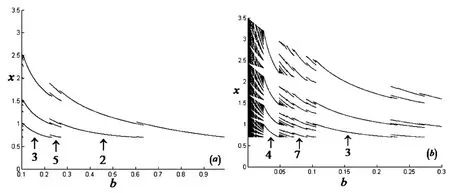
图2 a=5,c=0.7,x0=1.5(a)映射T(x)关于b的分岔序列,(b)局部放大图Fig.2 a=5,c=0.7,x0=1.5(a)Bifurcation sequence of map T(x)with parameter b,(b)Partially enlarged diagram of Fig.2(a)
2.1LRk序列下的边界碰撞分岔
对于分段映射,边界碰撞分岔会导致任意周期的环的出现或消失,而环的边界碰撞分岔条件则通过周期点碰撞不连续边界得到.以周期3环的边界碰撞分岔为例,如图3所示,只要x0∈[g(1),1],则周期3环存在,其周期点分别为x0<1,x1>x2>1.当周期点碰撞不连续边界后,周期3环发生边界碰撞分岔,其分岔条件为x0=1(如图3(a))和x2= 1(如图3(b)),x2=1也等价于x0=g(1).

图3 周期3环的边界碰撞分岔Fig.3 Border-collision bifurcation of a period-3 cycle
由以上分析可知:导致环出现或消失的两个边界碰撞分岔条件对应于吸引区间I=[c,a+b]的边界,即x0=1对应x1=f(x0)=a+b,x2=1对应x0=g(1)=c.
下面考虑周期k+1环,定义为{x0<1,x1>x2>…>xk>1}的边界碰撞分岔,即系统在边界的左边迭代1次,用符号L表示,在边界的右边迭代k次,用符号R表示,则周期k+1解的形式为LRk,而边界碰撞分岔条件由复合映射的不动点x0来决定,其迭代表达式如下:

通过迭代表达式,可知x0表示如下(其中d=1-b):

下面先考虑环LRk的存在条件,其次研究环LRk的边界碰撞分岔曲线.环的存在性通过x0∈[g(1),1]得出,即:





图4 c=0.7平面(a,b)上的LRk周期区域Fig.4 Periodic regions of LRkin the plane(a,b)for c=0.7
最后讨论环的稳定性,其稳定性条件如下:
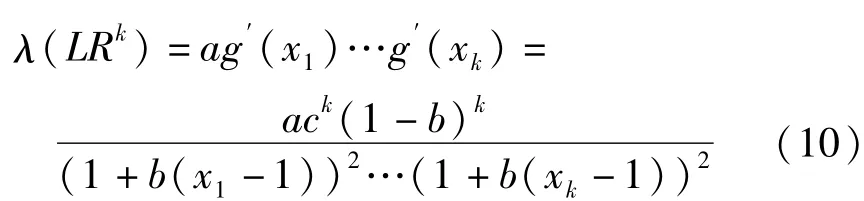
由于x1>x2>…>xk>1,故λ(LRk)<ack(1-b)k<1,则稳定性条件为:

2.2RLk序列下的边界碰撞分岔
本小节考虑周期k+1环,定义为{x0>1,x1<x2<…<xk<1},即系统在边界的左边迭代k次,用符号L表示,在边界的右边迭代1次,用符号R表示,则周期k+1环的表达式为RLk.而边界碰撞分岔条件由复合映射的不动点x0来决定,x0的表达式如下:

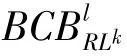


令A=f2-3eg,B=fg-9eh,C=g2-3fh,Δ=B2-4AC.根据一元三次方程的求根公式[19],(15)的根可以分为以下4种情况.
(ⅰ)当A=B=0时,


(ⅳ)当Δ=B2-4AC<0时,
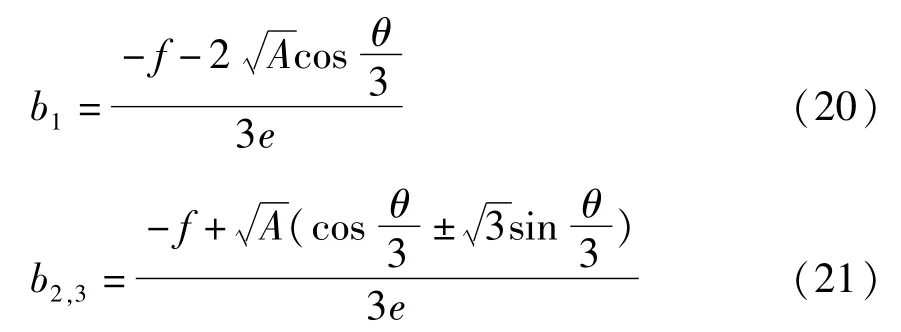
最后通过特征值确定环RLk的稳定性,结论如下:



环RLk发生fold分岔的条件如下:
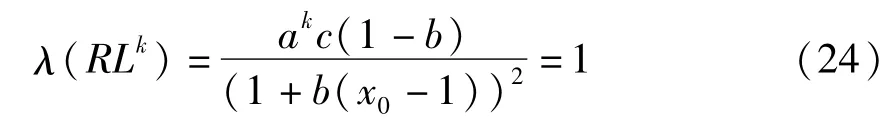
解得相应的x0为:


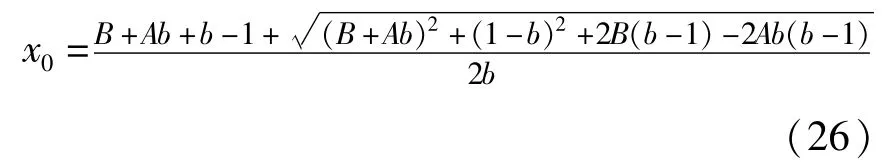
联立(25)(26),解得环RLk发生fold分岔时对应的参数范围:
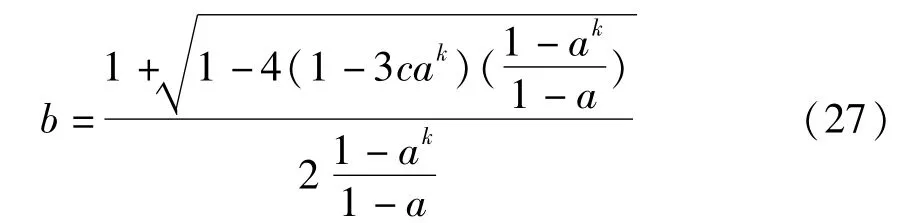
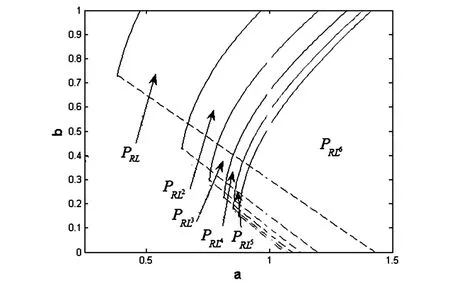
图5 c=0.7平面(a,b)上的RLk周期区域Fig.5 Periodicregions of RLkin the plane(a,b)for c=0.7
3 以c为分岔参数的边界碰撞分岔

本节讨论以c为分岔参数时,映射(2)的动力学行为.全局分岔图如图6所示,通过数值仿真观察到系统(2)存在周期增加序列,周期叠加序列,与以b为分岔参数的数值结果相同(如图2所示).
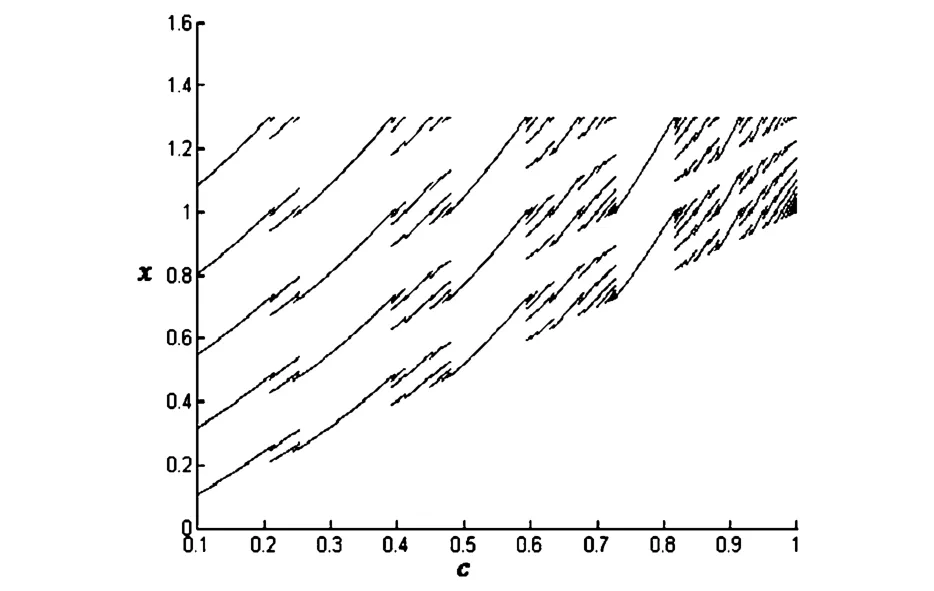
图6 a=1.1,b=0.2,x0=1.5映射T(x)关于c的分岔序列Fig.6 Bifurcation sequence of map T(x)with parameter b for a=1.1,b=0.2,x0=1.5
下面研究以c为分岔参数时,环RLk的边界碰撞曲线,边界超平面ξenv及大碰撞分岔(即无数条分岔曲线的交点).环LRk的讨论方法与RLk的讨论方法一样,故只讨论环RLk的边界碰撞分岔.

边界超平面ξenv由条件g(f(1))=f(g(1))得到:
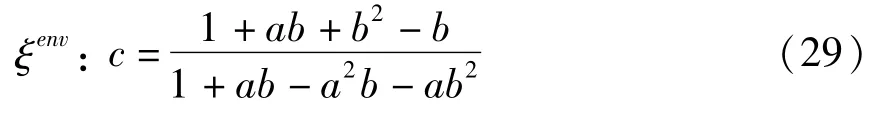

即在点BI(a)即发生大碰撞分岔.

图7 a=1.1平面(b,c)上的RLk周期区域Fig.7 Periodicregions of RLkin the plane(b,c)for a=1.1
4 三参数的分岔分析
本节将通过数值仿真,研究映射(2)的环的周期区域随3个参数改变的情况.


图8 平面(a,b)上环存在的周期区域随参数c改变的情况((a)c=0.1,(b)c=0.2 or 0.3,(c)c=0.4,(d)c=0.5,(e)c=0.6,(f)c=0.7~0.9)Fig.8 The change of periodic regions with the variation of parameter c in the plane(a,b)((a)c=0.1,(b)c=0.2 or 0.3,(c)c=0.4,(d)c=0.5,(e)c=0.6,(f)c=0.7~0.9)
图8(a)说明c=0.1时,系统(2)在b∈(0,0. 6)不存在任何的周期区域;图8(b)说明c=0.2或0.3时,系统(2)在b∈(0,0.6)存在周期2环的区域PLR;图8(c)说明c=0.4时,系统(2)在b∈(0,0.6)存在周期2环的区域PLR,周期3环的区域PLR2;图8(d)说明c=0.5时,系统(2)在b∈(0,0.6)存在周期2环的区域PLR,周期3环的区域PLR2,周期4环的区域PLR3;图8(e)说明c=0.6时,系统(2)在b∈(0,0.6)存在周期2环的区域PLR,周期3环的区域PLR2,周期4环的区域PLR3,周期5环的区域PLR4;图8(f)说明c=0.7~0.9时,系统(2)在b∈(0,0.6)存在周期2环的区域PLR,周期3环的区域PLR2,周期4环的区域PLR3,周期5环的区域PLR4,周期6环的区域PLR5,周期7环的区域PLR6.图8(a)~(f)说明了,环的周期随着参数c的增加而增加.


图9 平面(b,c)上环存在的周期区域随参数a改变的情况((a)a=1.1~1.6,(b)a=1.7or>1.7)Fig.9 The change of periodic regions with the variation of parametera in the plane(a,b)((a)a=1.1~1.6,(b)a=1.7or>1.7)
图9(a)(b)说明了系统(2)存在周期2环的区域PRL,周期3环的区域PRL2,周期4环的区域PRL3,周期5环的区域PRL4,周期6环的区域PRL5,周期7环的区域PRL6,环RL与环RL2共存的区域PRL∩PRL2,环RL2与环RL3共存的区域PRL2∩PRL3,环RL3与环RL4共存的区域PRL3∩PRL4,环RL4与环RL5共存的区域PRL4∩PRL5,环RL5与环RL6共存的区域PRL5∩PRL6,环RL与环RL2叠加的区域PRLRL2,环RL2与环RL3叠加的区域PRL2RL3,环RL3与环RL4叠加的区域PRL3RL4,环RL4与环RL5叠加的区域PRL4RL5,环RL5与环RL6叠加的区域PRL5RL6.不同之处在于图9(a)在a=1.1~1.6时,系统(2)存在曲线ξenv,而当a=1.7(或>1.7)时,图9(b)不存在曲线ξenv.
5 小结
对一类分段映射(2),在新的参数范围内,讨论了导致环RLk与环LRk出现或消失的边界碰撞分岔曲线及fold分岔条件,并且本文还综合考虑了各参数对系统动力学行为的影响,更加全面地揭示了系统的动力学特性.通过数值仿真,发现在新的参数范围内,系统不产生混沌,但是出现了周期环的周期增加、周期叠加现象.以上分析对全面了解分段映射(2)的动力学性质具有指导意义.
1 梁海花,郑伟峰.碰摩转子映射系统的非线性反馈混沌控制.动力学与控制学报,2007,5(1):30~33(Liang H H,Zheng W F.Nonlinear feedback control of chaos in rub-impact rotor mapping systems.Journal of Dynamics and Control,2007,5(1):30~33(in Chinese))
2 李志从,王琪.受两个频率激励和皮带驱动的具有干摩擦的振子的动力学分析.动力学与控制学报,2008,6(1):45~49(Li Z C,Wang Q.Dynamical analysis of a dry friction oscillator with two-frequency excitation and belt driving.Journal of Dynamics and Control,2008,6(1):45~49(in Chinese))
3 Nusse H E,Ott E,Yorke J A.Border-collision bifurcations:an explanation for observed bifurcations phenomena. Physical Review E,1994,49(2):1073~1076
4 Nusse H E,Yorke J A.Border-collision bifurcation including“period two to period three”for piecewise smooth systems.Physica D,1992,57(1):39~57
5 Feigin M I.The increasingly complex structure of the bifurcation tree of a piecewise-smooth system.Journal of Applied Mathematics and Mechanics,1995,59(6):853~863
6 di Bernardo M,Feigin M I,Hogan S J,Homer M E.Local analysis ofC-bifurcationsinn-dimensionalpiecewisesmooth dynamical systems.Chaos,Solitons&Fractals,1999,10(11):1881~1908
7 Chin W,Ott E,Nusse H E,Grebogi C.Grazing bifurcations in impact oscillators.Physical Review E,1994,50(6):4427~4444
8 de Weger J,van de Water W,Molenaar J.Grazing impact oscillations.Physical Review E,2000,62(2):2030~2041
9 Gardini L,Tramontana F,Banerjee S.Bifurcation analysis of an inductorless chaos generator using 1D piecewise smooth map.Mathematics and Computers in Simulation,2013,95:137~145
10 Avrutin V,Dutta P S,Schanz M,Banerjee S.Influence of a square-root singularity on the behaviour of piecewise smooth maps.Nonlinearity,2010,23(2):445~463
11 Sushko I,Agliari A,Gardini L.Bifurcation structure of parameter plane for a family of unimodal piecewise smooth maps:Border-collision bifurcation curves.Chaos,Solitons &Fractals,2006,29(3):756~770
12 Gardini L,Tramontana F,Sushko I.Border-collision bifurcations in one dimensional linear-hyperbolic maps. Mathematics and Computers in Simulation,2010,81(4):899~914
13 Gardini L,Sushko I,Naimzada A K.Growing through chaotic intervals.Journal of Economic Theory,2008,143(1):541~557
14 Gardini L,Tramontana F.Border-collision bifurcation curves and their classification in a family of 1D discontinuous maps.Chaos,Solitons&Fractals,2011,44(4-5):248~259
15 Tramontana F,Gardini L.Border-collision bifurcations in discontinuous one dimensional linear-hyperbolic maps. Communications in Nonlinear Science and Numerical Simulation,2011,16(3):1414~1423
16 Tramontana F,Gardini L,Agliari A.Endogenous cycles in discontinuous growth models.Mathematics and Computers in Simulation,2011,81:1625~1639
17 Bischi G I,Gardini L,Tramontana F.Bifurcation curves in discontinuous maps.Discrete and Continuous Dynamical Systems,Series B,2010,13(2):249~267
18 Avrutin V,Schanz M,Banerjee S.Multi-parametric bifurcations in a piecewise linear discontinuous map.Nonlinearity,2006,19:1875~1906
19 范盛金.一元三次方程的新求根公式与新判别法.海南师范学院学报(自然科学版),1989,2(2):91~98(Fan S J.A new extracting formula and a new distinguishing means on the one variable cubic equation.Natural Science Journal of Hainan Teachers College,1989,2(2):91~98(in Chinese))
BIFURCATION ANALYSIS IN A CLASS OF DISCONTINUOUS MAPS*
Li Qunhong†Wei Limei Lu Yumu
(College of Mathematics and Information Science,Guangxi University,Nanning 530004,China)
Border-collision bifurcations of a class of one-dimensional piecewise discontinuous maps were investigated.The border-collision bifurcation curves and fold bifurcation conditions for period-n solutions were derived. The correctness of the deduced results was confirmed through the numerical simulations.It is found that there are period adding sequences and period overlapping sequences in the system.Finally,the three-parameter bifurcations of the piecewise discontinuous map were considered,which demonstrates the combined influence of all the parameters in the map.
piecewise map,border-collision bifurcation,period overlapping,period adding
26 January 2014,revised 3 April 2014.
E-mail:liqh@gxu.edu.cn
10.6052/1672-6553-2014-021
2014-01-26收到第1稿,2014-04-03收到修改稿.
*国家自然科学基金资助项目(10972059和11372077)和广西自然科学基金资助项目(2010GXNSFA013110和2013GXNSFAA019017)
E-mail:liqh@gxu.edu.cn
*The project supported by the National Natural Science Foundation of China(10972059 and 11372077)and the Guangxi Natural Science Foundation(2010GXNSFA013110 and 2013GXNSFAA019017)

