平面框架结构折线型弹塑性动力学非传统Hamilton型增量变分原理*
姜凤华罗恩
(1.台州学院建筑工程学院,台州 318000)(2.中山大学应用力学与工程系,广州 510275)
平面框架结构折线型弹塑性动力学非传统Hamilton型增量变分原理*
姜凤华1†罗恩2
(1.台州学院建筑工程学院,台州 318000)(2.中山大学应用力学与工程系,广州 510275)
根据古典阴阳互补和现代对偶互补的基本思想,通过罗恩提出的一条简单而统一的新途径,系统地建立了平面框架结构折线型弹塑性动力学的各类非传统Hamilton型变分原理.文中首先给出平面框架结构折线型弹塑性动力学的广义虚功原理的表式,然后从该式出发,不仅能得到平面框架结构折线型弹塑性动力学的虚功原理,而且通过所给出的广义Legendre变换,还能系统地成对导出平面框架结构折线型弹塑性动力学的5类变量分原理的互补泛函,以及1类变量和相空间非传统Hamilton型变分原理的泛函.同时,通过这条新途径还能清楚地阐明这些原理的内在联系.
框架结构,弹塑性动力学,相空间,非传统Hamilton型变分原理,初值-边值问题
引言
结构的弹塑性分析一般都相当复杂,因此,目前大多数都将非线性的本构关系简化为分段线性弹性的本构关系.对于平面框架折线型弹塑性动力学,可建立相应的增量变分原理,然后采用基于增量变分原理的增量有限元法进行分析.
对于静力学增量变分原理的研究,1976年Horrigmoe和Bergan[1]在传统变分原理的基础上通过考虑增量变形来解决非线性问题,并与有限元结合,放松单元的连续性要求,修正了传统的增量变分原理;同年,Pian[2]给出了小位移问题增量变分原理和放松连续性要求的修正的增量变分原理;1980年Mason[3]给出了固体力学和壳体理论中的增量能量方法,明确提出了增量变分原理的概念,并给出了两条得到增量变分原理的途径;1984年刘正兴[4]建立了基于增量变分原理的柔韧梁和柔韧板单元;钟万勰[5]给出了小位移弹性问题中的各类增量变分原理;1993年Grzegorz[6]给出了线弹性摩擦接触问题的增量变分原理;2007年Lahellec和Suquet[7]给出了非线性非弹性复合材料的增量变分原理.2000年贺国京和陈大鹏[8]提出了结构非线性振动的杂交混合幅值增量变分原理.但是,有关框架结构的一些重要的增量型基本原理,例如增量虚功原理和能反映其初值-边值问题的全部特征各类非传统Hamilton型增量变分原理至今国内外还没有系统建立.
本文根据文献[9]提出的一条简单而统一的新途径,系统地建立了框架结构折线型弹塑性动力学的广义增量虚功原理和增量虚功原理、以及各类非传统Hamilton型增量变分原理和相空间非传统Hamilton型增量变分原理.这种新的增量变分原理能反映这种动力学初值-边值问题的全部特征.
1 平面框架折线型弹塑性动力学基本方程及条件
(1)速度位移关系

式中v=[vs,vr]T,u=[us,ur]T.
(2)动量速度关系

式中p=[ps,pr]T.
(3)运动方程


(4)广义应变与位移关系
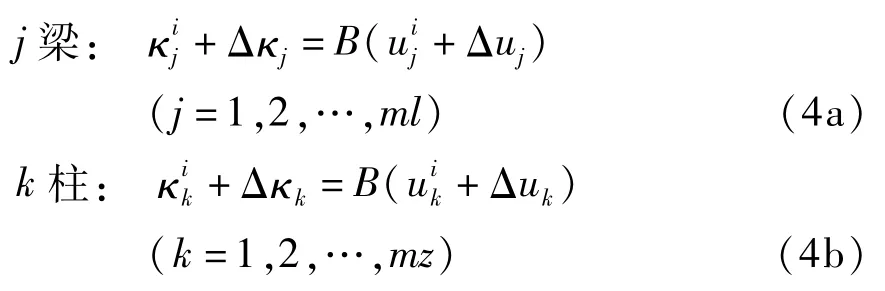
式中=[εs,κ]T.
(5)广义内力和广义应变关系
对于一般弹塑性问题,有

式中,Φ(κ)和Ψ(Q)分别为应变能密度和余应变能密度.
将增量段的广义内力和广义应变关系线性化,一般弹塑性问题简化为折线型弹塑性问题后,有:


图1 折线型弯矩曲率关系Fig.1 Piecewise linear relationship of moment-curvature
(6)结构边界条件
对于结构的整体直角坐标系x,z,给定节点外力的节点条件和给定节点位移的支撑节点条件分别为:

(7)初始条件

(8)梁柱交结点的联结条件
①梁柱交结点的位移协调条件:

②梁柱交结点的力平衡条件:
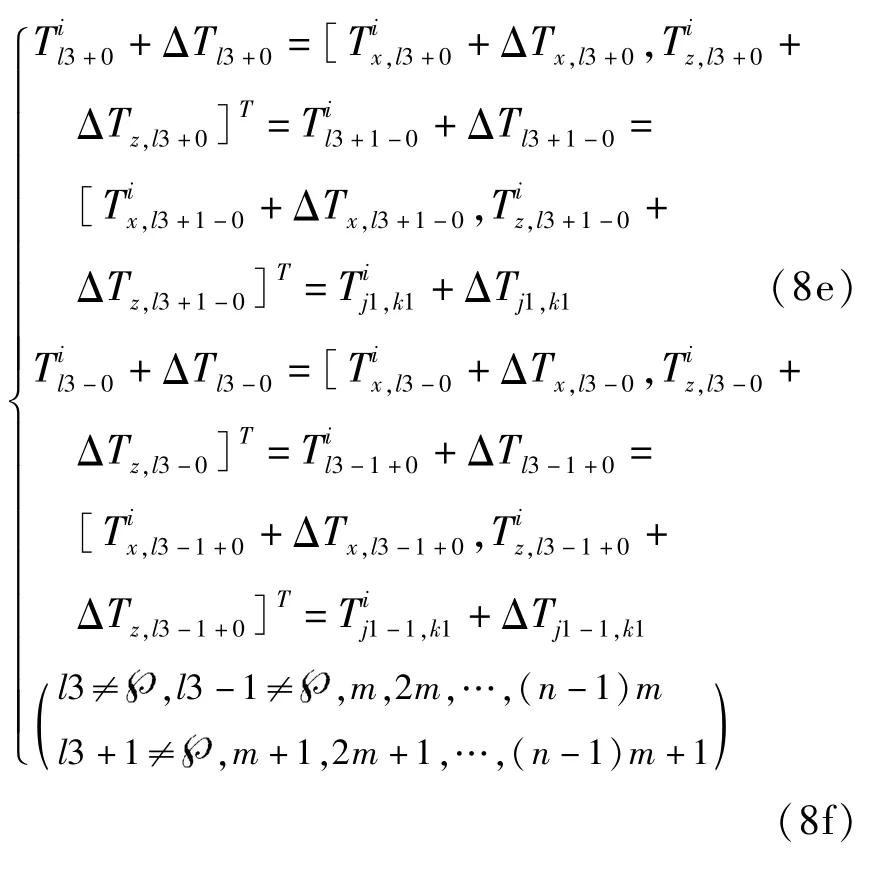

2 增量广义虚功原理、增量虚功原理
可以证明,对于任意无关的p,Q,u,有下列积分关系式成立:

上式即为平面框架结构动力学的广义虚功原理.
根据(9)式,对于互不相关的任意函数pi,Qi,ui可得
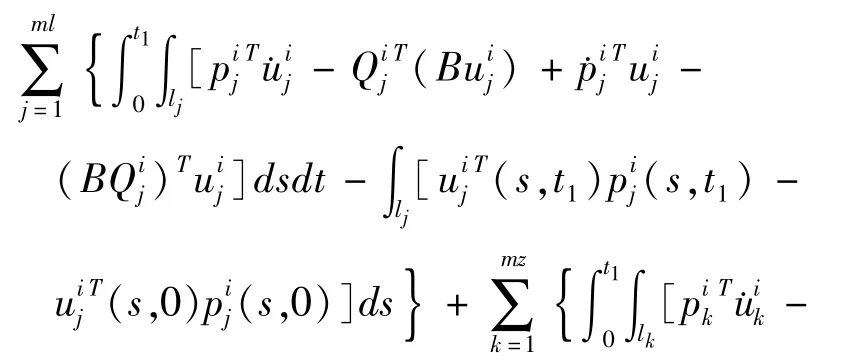
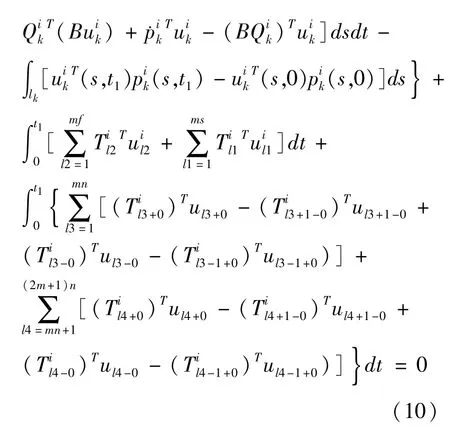
对于互不相关的任意函数pi+Δp,Qi+ΔQ,ui+Δu可得

将式(11)和式(10)相减,可得

式(12)是本文给出的一个重要关系式,在力学上可称为平面框架结构动力学增量广义虚功原理.从该式出发,不仅能系统建立增量虚功原理和平面框架结构材料非线性动力学的非传统Hamilton型增量变分原理,而且能清楚地阐明这些原理之间的内在联系.
当Δp,ΔQ满足方程(3a,c)和条件(6b),(7b,d),(8e-h);Δu满足方程(1a,b),(4a,b)和条件(6a),(7a,c),(8a-d)时,由式(12)可得

式(13)可以看成是平面框架结构动力学增量虚功原理的表式,它反映广义动力可能状态与广义运动可能状态之间的最一般关系,或者说,它反映阴变量Δu,Δv,Δκ与阳变量Δf,Δp,ΔQ这两组对偶变量之间的最一般关系.
3 平面框架结构折线型弹塑性动力学增量变分原理
3.15类变量增量变分原理
对于互不相关的任意函数p和v,有下列关系式:

式中,K(v)=ρAvTv/2,K*(p)=pTp/2ρA,B(v,p)=(ρAv-p)T(ρAv-p)/2ρA,K(v)和K*(p)分别为动能密度和余动能密度.
根据式(14),对于增量段,可得

将式(14c)和式(14b)相减,可得


式中

其中
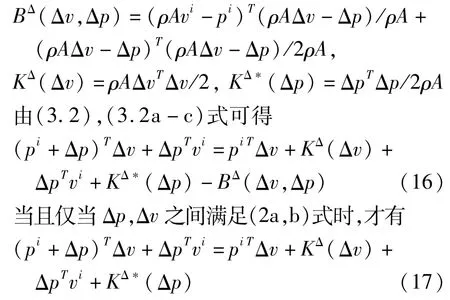
当Q与κ分别是互不相关的任意函数时,可以得到下列关系式

式中

根据式(18a),对于增量段,可得

将式(19b)和式(19a)相减,可得

考虑到增量段线性化的广义内力与广义应变关系,于是有

式中

同理

式中

而

式中
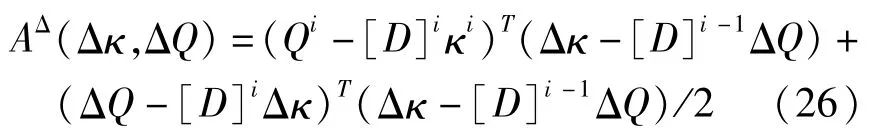
由式(19)~(26)可得

当且仅当ΔQ和Δκ之间满足式(5)时,才有

上述的(17)和(27)式是本文给出的广义Legendre变换式.


将式(12)的T2-T3+T5-T6+T7+T8变换为
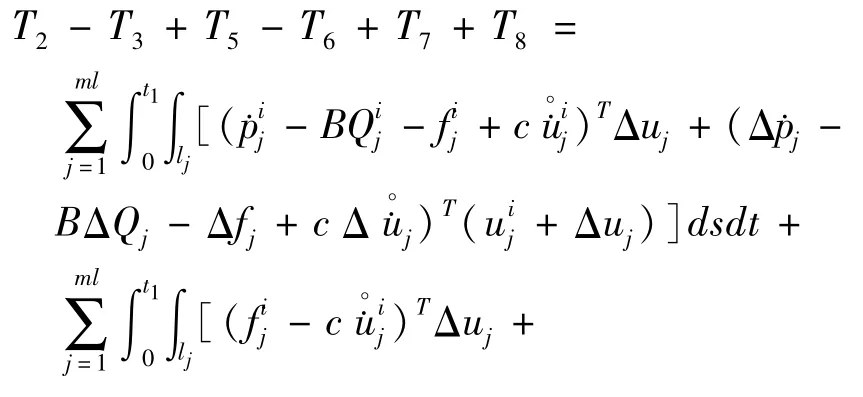
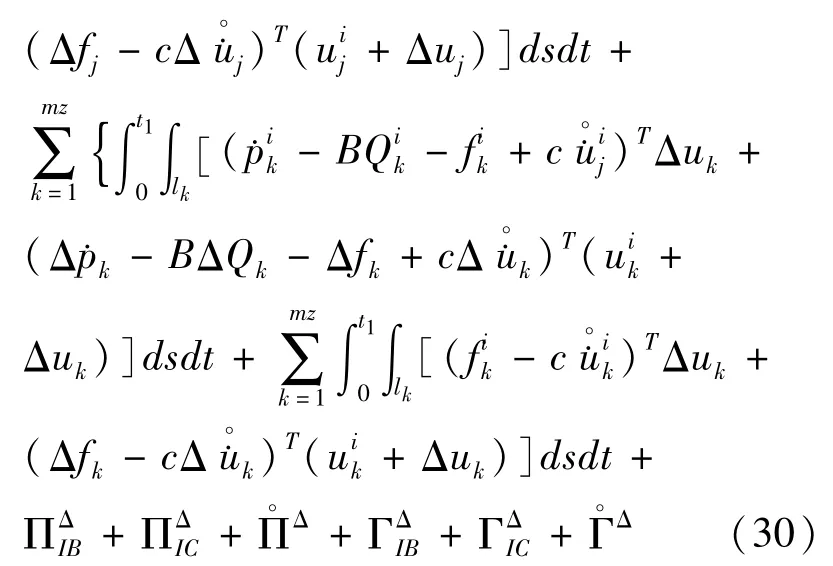
式中



其中带上标°的量为限制变分量.



定理1 当且仅当Δp,Δv,ΔQ,Δκ,Δu是混合问题(1a,b),(2a,b),(3a,c),(4a,b),(5a,c),(6a,b),(7a-d),(8a-h)式的解,则必定满足下列变分式

证明 将(31b)式对自变函数Δp,Δv,ΔQ,Δκ,Δu变分,可得



3.21类变量增量变分原理
当Δp,Δv,Δu满足(1a,b)和(2a,b)式,Δκ,,注意到(33)式,由于δΔp,δΔv,δΔQ,δΔκ,δΔu的任意性,并根据变分法的有关引理,故由此可得(1a,b),(2a,b),(3a,c),(4a,b),(5a,c),(6a,b),(7a-d),(8a-h)式,即Δp,Δv,ΔQ,Δκ,Δu是混合问题(1a,b)~(8a-h)式的解. Δu满足(4a,b)式时,泛函就变成为



3.3相空间非传统Hamilton型增量变分原理
当Δp与Δv和Δκ与Δu分别满足(2a,b)式和(4a,b)式时,泛函就变为

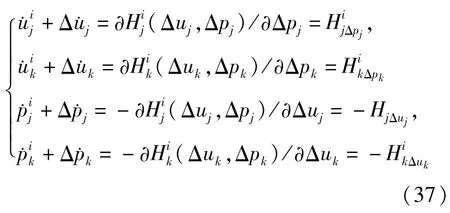
或者

和边界条件(6a,b)与初始条件(7a-d)及联结条件(8a-h).

为了揭示Hamilton正则方程的数学结构,就要打破传统概念的限制,引进新概念.为此,将(37)式写成矩阵形式

式(39)揭示了Hamilton正则方程和相应的相空间非传统Hamilton变分原理都具有自然辛结构.
4 结语
本文所建立的平面框架结构折线型弹塑性动力学各类变量非传统Hamilton型增量变分原理都是限制变分原理,它们能反映空间框架结构弹性动力学初值-边值问题的全部特征.文中所建立的这些新的增量变分原理,不仅在平面框架结构动力学理论及建立有关工程实用理论方面有重要的意义,而且为建立基于增量变分原理的直接解法,如有限元法等提供了重要的理论基础.因篇幅所限,有关这些变分原理的应用研究,将另文阐述.
1 Horrigmoe G,Bergan P G.Incremental variational principles and finite element models for nonlinear problems. Computer Methods in Applied Mechanics and Engineering,1976,7(2):201~217
2 Pian T H H.Variational principles for incremental finite element methods.Journal of the Franklin Institute,1976,302(5-6):473~488
3 Mason J.Variational incremental and energy Methods in solid mechanics and shell theory.Amsterdam:Elsevier Scientific Publisher Company,1980
4 刘正兴.基于增量变分原理的柔韧梁和柔韧板单元.计算结构力学及其应用,1984,1(4):49~59(Liu Z X. Flexible beam and fexible plate element based on incremental variational principle.Computational Structural Mechanics and Application,1984,1(4):49~59(in Chinese))
5 钟万勰.数值计算方法.北京:中国建筑工业出版社,1991:15~20(Zhong W X.Calculating numerical method.Beijing:China Architecture Building Press,1991:15~20(in Chinese))
6 Grzegorz Z.The incremental variational principle and finite element displacement approximation for the frictional contact problem of linear elasticity.International Journal of Non-Linear Mechanics,1993,28(1):13~28
7 Lahellec N,Suquet P.On the effective behavior of nonlinear inelastic composites:I.Incremental variational principles.Journal of the Mechanics and Physics of Solids,2007,21(5):85~89
8 贺国京,陈大鹏.结构非线性振动的杂交/混合幅值增量变分原理.铁道学报,2000,22(2):60~66(He G W,Chen D P.Hybrid/mixed amplitude incremental variational principle for nonlinear vibration of structures.Journal of theChina Railway Society,2000,22(2):60~66(in Chinese))
9 罗恩.关于线弹性动力学中各种Gurtin型变分原理.中国科学(A辑),1987(9):936~948(Luo E.On the Gurtin-type variational principles in linear elastodynamics.Science in China(Series A),1987(9):936~948(in Chinese))
10 姜凤华,罗恩.分段线性弹性薄板动力学非传统Hamilton型变分原理.振动与冲击,2008,27(11):109~114(Jiang F H,Luo E.The unconventional Hamilton-type incremental variational principles for piecewise linear elstodynamics of thin plates.Journal of Vibration and Shock,2008,27(11):109~114(in Chinese))
THE UNCONVENTIONAL HAMILTON-TYPE INCREMENTAL VARIATIONAL PRINCIPLES FOR PIECEWISE LINEAR ELASTODYNAMICS OF FRAME STRUCTURE*
Jiang Fenghua1†Luo En2
(1.School of Engineering and Architecture,Taizhou University,Taizhou 318000,China)
(2.Department of Applied Mechanics and Engineering,Zhongshan University,Guangzhou 510275,China)
According to the basic idea of classical yin-yang complementarity and modern dual-complementarity,in a simple and unified new way proposed by Luo,the unconventional Hamilton-type incremental variational principles for broken line elasto-plastic dynamics of frame structure can be established systematically.The unconventional Hamilton-type incremental variational principle can fully characterize the initial-boundary-value problem of broken line elasto-plastic dynamics of frame structure.In this paper,an important integral relation was given,which can be considered as the expression of the generalized principle of virtual work for broken line elasto-plastic dynamics of frame structure.Based on this relation,it is possible to derive systematically the complementary functionals for five-field,and the functional for one-field unconventional Hamilton-type incremental variational principles and the unconventional Hamilton-type incremental variational principle in phase space by the generalized Legendre transformations were also given.Furthermore,with this new approach,the intrinsic relationship among various principles can be explained clearly.
frame structure,elasto-plastic dynamics,phase space,unconventional Hamilton-type incremental variational principle,initial-boundary-value problem
25 May 2013,revised 17 June 2013.
E-mail:jfhzsu@tzc.du.cn
10.6052/1672-6553-2014-016
2013-05-25收到第1稿,2013-06-17收到修改稿.
*国家自然科学基金资助项目(10772203)和浙江省科技厅公益技术应用研究资助项目(2011C31032)
E-mail:jfhzsu@tzc.du.cn
*The project supported by the National Natural Science Foundation of China(10772203)and the Public Eechnology Applied Research Foundation of Science technology Department of Zhejiang province(2011C31032)

