复合材料悬臂外伸板的非线性动力学建模及数值研究*
吕书锋 张伟
(北京工业大学机电学院,北京 100124)
复合材料悬臂外伸板的非线性动力学建模及数值研究*
吕书锋 张伟†
(北京工业大学机电学院,北京 100124)
研究了横向气动载荷和参数激励联合作用下复合材料悬臂外伸矩形板在伸出过程中的非线性动力学问题.根据Reddy的高阶剪切层合板理论,应用Hamilton原理建立了外伸板在横向气动力和参数激励作用下的非线性动力学方程,其中横向气动力采用一阶活塞气动力.然后应用Galerkin方法对系统偏微分形式的非线性方程进行离散,得到了一组时变系数的非线性动力学方程.在此方程的基础上,对复合材料悬臂外伸板进行了数值模拟分析,讨论了外伸速度对悬臂外伸板非线性动力学特性的影响.
复合材料悬臂外伸板,高阶剪切理论,活塞理论,Hamilton原理,非线性动力学
引言
近年来,轴向悬臂外伸结构在工程中的应用越来越常见,如新型可变形机翼、太阳帆板和天线、机械手臂等.这类结构因其沿轴向是可运动的,相比于不可移动、静止的结构,当其沿轴向运动或受到外载荷的作用时,可能带来一些新的、影响结构稳定性的动力学问题.因此研究其运动过程中的非线性动力学特性对工程应用具有很重要的价值.
近年来,轴向悬臂可外伸结构的研究已引起了学者们的关注.Tabarrok等[1]推导了长度随时间变化梁的运动方程,得到四个非线性偏微分形式运动方程和一个几何关系方程.Taleb和Misra[2]研究了不可压缩流体中,以恒定速度外伸的等环形截面悬臂梁的小变形横向振动.Wang和Wei[3]将一个柔性机械手臂建模为细长的可移动悬臂梁模型,研究了梁在外伸过程中的运动特性.Fung等[4]利用四种不同的梁理论建立了带尖端质量移动梁的非线性动力学模型.Theodore等[5]根据Euler-Bernoulli梁理论推导了轴向可外伸柔性梁的运动方程,并通过数值模拟的方法研究了其横向振动.Behdinan和Tabarrok等[6]应用Hamilton原理推导了可外伸柔性梁的运动方程.Gosselin等[7]研究了等环形截面柔细悬臂梁在不可压缩稠密流体中以恒定速度伸展的稳定性.研究类似模型的还有,Poivan和Sampaio[8]研究了轴向运动功能梯度柔性梁的振动问题.Wang等[9]推导了一种可外伸悬臂板模型线性振动的动力学方程,分析了运动过程中的频率和系统稳定性.张谦等[10]设计了一种可外伸机翼结构,实验研究了该结构在不同外伸速度下的动力学响应.本文选取沿轴向可外伸的复合材料悬臂矩形板作为研究对象,对其在活塞气动力[11]和面内参数激励联合作用下的非线性振动特性进行分析.
1 基本方程
考虑一个沿轴向可外伸的复合材料层合矩形悬臂板,该板受到面内均布简谐激励和横向气动载荷共同作用.板以初始长度l0开始沿x轴方向悬臂向外伸出,板宽为b,厚度为h,笛卡尔坐标系Oxy位于板的中面,如图1所示.外伸速度考虑了一个小扰动的影响,形式为V=V0+Vdcos(Ω2t),面内激励的形式为fy=f0+f1cosΩ1t,横向的气动力载荷采用一阶活塞气动力,记为Δp.
根据Reddy的高阶剪切层合板理论[12],位移场可以写为

其中,u0,v0,w0为中面上任意一点分别沿x,y,z方向的位移,φx和φy分别为绕y和x轴的转角.
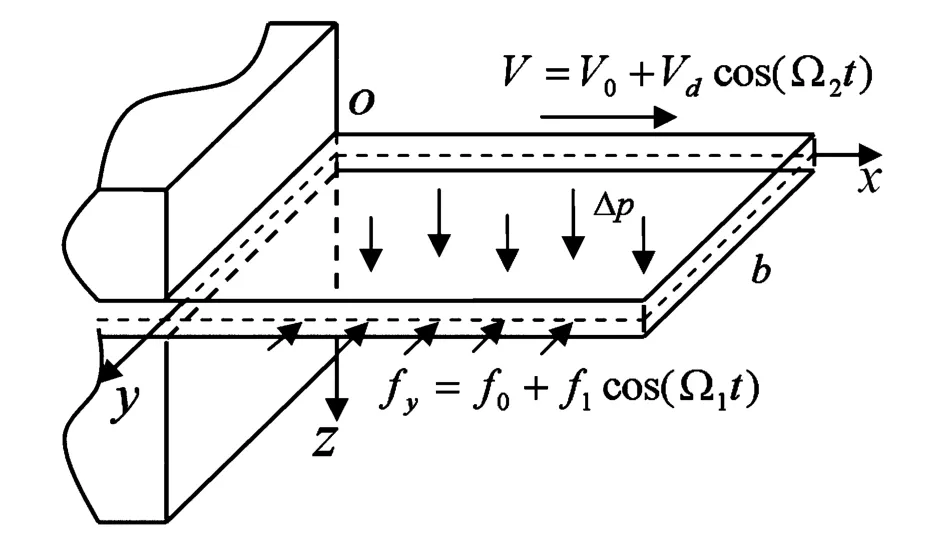
图1 悬臂外伸板的力学模型Fig.1 The model of deploying cantilever plate
采用von Karman的大变形几何关系,可以得到应变-位移关系εi(i=xx,yy)和曲率-位移关系γi(i=xy,yz,zx)的表达式

根据Hamilton原理,可推得可伸缩悬臂板的非线性动力学方程为
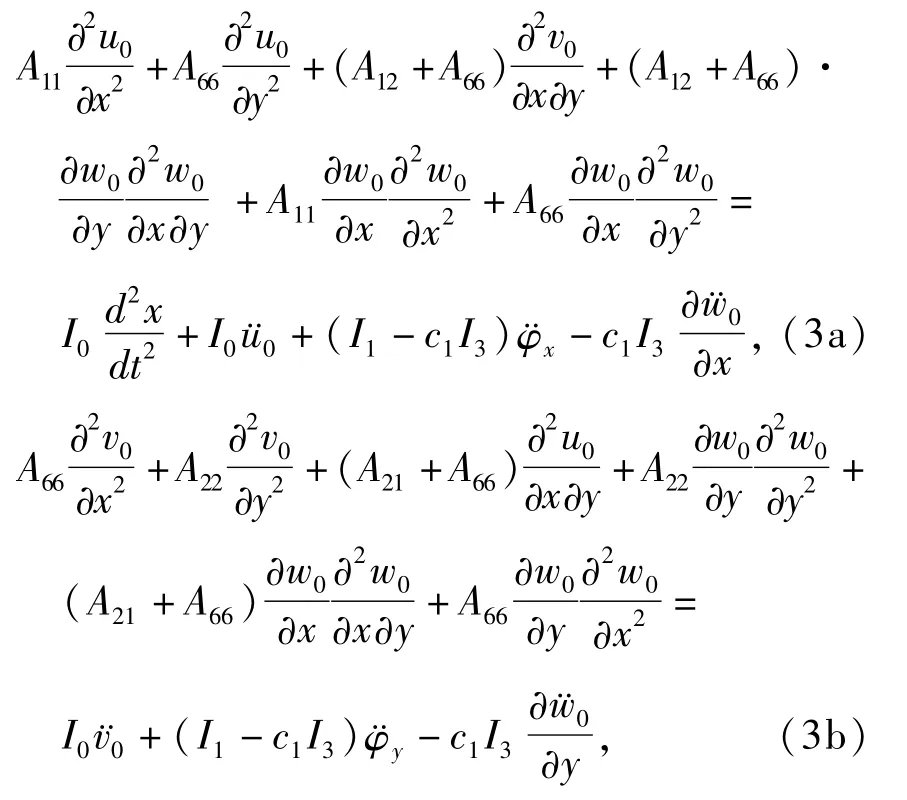

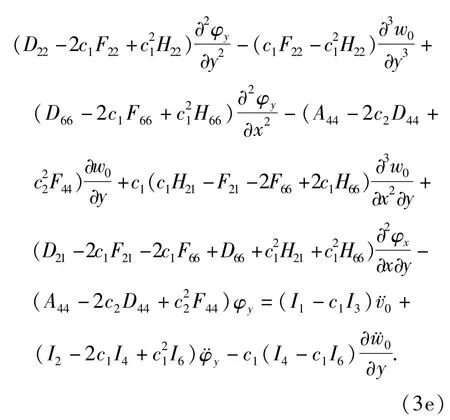
其中,δ为阻尼系数,Δp表示由一阶活塞理论推得的气动载荷,形式为

悬臂外伸板在固定和自由端的边界条件分别为

2 Galerkin离散
对方程(3)进行无量纲化,然后应用Galerkin方法将偏微分形式的非线性方程离散为常微分形式的非线性动力学方程.本文选取了系统前两阶振动模态进行二阶Galerkin离散,在满足位移边界条件的情况下选取振型函数为


其中,Xi(x)取沿x方向的固支-自由梁函数,Yj(y)取沿y方向的自由-自由梁函数.
将振型函数(6)代入方程(3)进行Galerkin运算的过程中,特别需要注意,因为板的长度沿x轴是随时间改变的,所以在推导中要用到如下运算关系
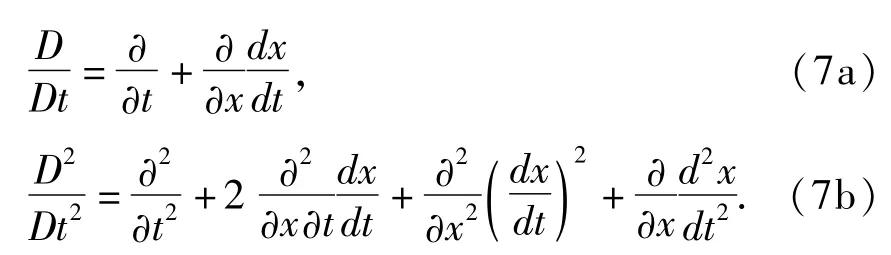
考虑横向振动为系统的主要运动方式,离散后可以得到以横向位移w1和w2为变量的两自由度无量纲非线性动力学方程

这里,方程中的系数αi和βi(i=1,2,…,10)都是与时间有关的变量,即得到的方程是变系数系统,方程的质量项、阻尼项和刚度项都随时间变化.
3 算例分析
为了研究复合材料悬臂外伸板的非线性动力学特性,选取如下参数进行数值分析.板的组成为各铺层等厚度、同材料、正交铺设的三层石墨/环氧,其它参数:l0=2.0m,b=1.5m,h=0.004m,f0= 2000N/m2,Vd=0.005m/s,Ω1=Ω2=15,κ=1.4,M∞=3.0,Va=900m/s,ρa=0.65kg/m3,δ=600N ·s/m.根据非线性振动方程(8),数值分析相关参数对系统外伸过程中动力学稳定性的影响.
图2与图3给出了两种不同外伸速度下悬臂板沿轴向外伸过程中第一阶和第二阶振动的时域分析曲线.首先观察这些图的全局响应特性,尽管外伸速度的取值不同,系统的整个外伸过程呈现出一些相似的振动规律,即初始的时候,系统会发生振幅的跳跃现象,随着板的继续外伸,系统的第一阶振动幅值逐渐增大,第二阶振动幅值先减小再增大,前两阶振动频率逐渐降低,振幅可能再次发生跳跃和发散现象.
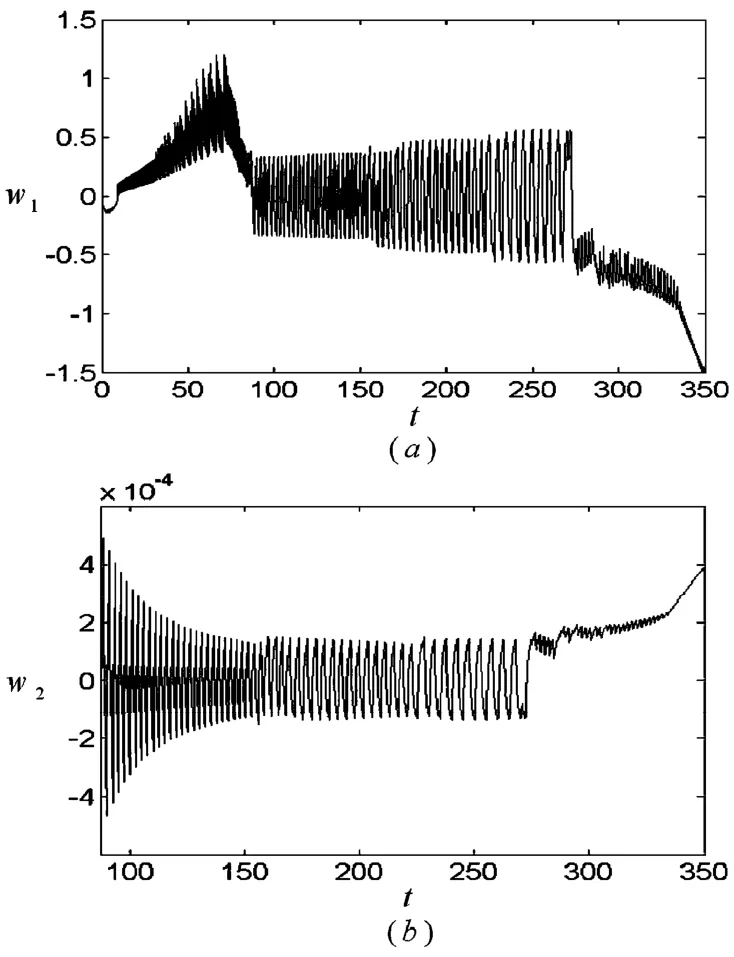
图2 当V0=0.10时系统的时间历程图Fig.2 Time history curves when V0=0.10
通过对两种不同速度下系统时间历程图的比较,可以发现外伸速度对系统外伸过程中动力学稳定性的影响.首先观察系统的第一阶振动,当外伸速度为v0=0.10m/s时,如图2(a),在无量纲时间t=90左右,振幅结束初始跳跃,当外伸速度增大到v0=0.20m/s时,见图3(a),振幅结束跳跃的无量纲时间大约为t=80,显而易见,随着外伸速度的增加,振幅结束初始跳跃的时间逐渐提前.但与此同时,系统振幅再次发生跳跃的时间会提前,并且外伸速度越快,系统再次发生振幅跳跃的时间就越提前.
对于第二阶振动而言,运动规律与第一阶的运动形式相似,如图2(b)、3(b).相比而言,第二阶振动的振幅远小于第一阶振幅,可见第一阶振动为系统的主要振动形式.

图3 当V0=0.20时系统的时间历程图Fig.3 Time history curves when V0=0.20
4 结论
本文考虑一个沿轴向可外伸的复合材料悬臂板模型,应用高阶剪切理论和Hamilton原理建立其动力学方程,根据得到的时变系数方程,应用数值模拟的方法研究了一阶活塞气动力作用下系统的非线性动力学响应.研究发现:悬臂板在外伸过程中,前两阶振动频率逐渐降低,存在振幅跳跃和发散的现象.并且随着外伸速度的增大,系统的振幅结束初始跳跃的时间逐渐提前,同时再次发生振幅跳跃的时间也会提前.
1 Tabarrok B,Leech C M,Kim Y I.On the dynamics of an axially moving beam.Journal of the Franklin Institute,1974,297:201~220
2 Taleb I A,Misra A K.Dynamics of an axially moving beam submerged in a fluid.Journal of Hydronautics,1981,15:62~66
3 Wang P K C,Wei J D.Vibration in a moving flexible robot arm.Journal of Sound and Vibration,1987,116(1):149~160
4 Fung R F,Lu P Y,Tseng C C.Non-linearly dynamic modeling of an axially moving beam with a tip mass.Journal of Sound and Vibration,1998,218:559~571
5 Theodore R J,Arakeri J H,Ghosal A.The modelling ofaxially translating flexible beams.Journal of Sound and Vibration,1996,191(3):363~376
6 Behdinan K,Tabarrok B.Dynamics of flexible sliding beams-nonlinear analysis,Part II:transient response. Journal of Sound and Vibration,1997,208(4):541~565
7 Gosselin F,Paidoussis M P,Misra A K.Stability of a deploying/deploying beam in dense fluid.Journal of Sound and Vibration,2007,299:123~142
8 Poivan M,Sampaio T R.Vibrations of axially moving flexible beams made of functionally graded materials.Thinwalled Structures,2008,46:112~121
9 Wang L H,Hu Z D,Zhong Z.Dynamic analysis of an axially translating plate with time-variant length.Acta Mechanica,2010,215:9~23
10 张伟,张谦,曹东兴.可伸缩机翼结构设计与振动实验研究.动力学与控制学报,2011,9(4):326~330(Zhang W,Zhang Q,Cao D X.Structural design and vibration experimental investigation of telescopic wings. Journal of Dynamics and Control,2011,9(4):326~330(in Chinese))
11 Ashley H,Zartarian G.Piston theory a new aerodynamic tool for the aeroelastician.Journal of Aeronautical Sciences,1956,23:1109~1118
12 Reddy J N.Mechanics of laminated composite plates and shells:Theory and Analysis.Boca Raton:CRC Press LLC,2004
NONLINEAR ANALYSIS OF DEPLOYING LAMINATED COMPOSITE CANTILEVER PLATES*
Lu Shufeng Zhang Wei†
(College of Mechanical Engineering,Beijing University of Technology,Beijing 100124,China)
This paper studied the nonlinear dynamics of deploying cantilever laminated composite plates subjected to transversal aerodynamic pressures and in-plane excitations.The first-order piston theory was employed to model the transversal air pressures.Based on Reddy′s third-order shear deformable plate theory and Hamilton Principal,the nonlinear governing equations of motion were established for the deploying cantilever laminated composite plates.By choosing suitable vibration mode-shape functions,the two-degree-of-freedom nonlinear governing equations of motion with time-varying coefficients were deduced by using Galerkin method.The influences of varying deploying velocities on the nonlinear resonance of the deploying cantilever plate were analyzed.
axially moving cantilever laminated plates,third-order plate theory,piston theory,Hamilton principle,nonlinear dynamics
26 July 2013,revised 5 December 2013.
E-mail:sandyzhang0@yahoo.com
10.6052/1672-6553-2014-040
2013-07-26收到第1稿,2013-12-05收到修改稿.
*国家自然科学基金资助项目(11290152,11072008和10732020)
E-mail:sandyzhang0@yahoo.com
*The project supported by the National Natural Science Foundation of China(11290152,11072008 and 10732020)

