Pre-Bötzinger复合体中耦合神经元簇同步模式及转迁的分岔分析*
袁丹丹 陈汐 段利霞
(北方工业大学理学院,北京 100144)
Pre-Bötzinger复合体中耦合神经元簇同步模式及转迁的分岔分析*
袁丹丹 陈汐 段利霞†
(北方工业大学理学院,北京 100144)
Pre-Bötzinger复合体中兴奋性神经元节律性簇放电与呼吸节律的产生关系密切.泄漏电流对神经元簇放电具有重要的调节作用.本文利用双参数分岔分析和快慢变量分离等方法,研究了泄漏电流对耦合神经元簇同步模式及其转迁机制的影响.结果表明,在不同初始条件下,当泄漏电导改变时耦合神经元分别表现为同相“fold/homoclinic”型、“subHopf/homoclinic”型和反相“fold/fold cycle”型和“subHopf/fold cycle”型簇放电.本文的研究为进一步探索呼吸节律的产生机制提供了一些见解.
簇放电,双参数分岔,快慢变量分离,pre-Bötzinger复合体,呼吸节律
引言
位于哺乳动物脑干中的pre-Bötinger复合体(pre-Bötzinger complex)是呼吸节律产生的中枢,其中存在着一类吸气神经元[1],这类神经元具有振荡簇发放的内在特性和类似心脏起搏器的兴奋性特性[1-2].突触连接的耦合神经元会呈现簇同步,耦合神经元集群能够通过它们的同步行为,自主地按一定的频率发出冲动.这些耦合神经元之间互相联系,协调一致地调节呼吸运动[3].
簇放电是神经元最重要的放电模式之一,它比单个峰放电携带更多的信息而成为科研者关注的一种重要的节律放电模式.Pre-Bötzinger复合体中,当引入突触耦合时,神经元会产生同相同步和反相同步两种同步模式[4].当耦合强度较小时,神经元的同步放电模式又可分为对称和非对称的放电模式[4].耦合神经元簇同步模式对单个神经元的放电模式具有不同的依赖性[5,6].在pre-Bötzinger复合体中,神经元的动力学本质和网络拓扑结构的交互作用对神经元簇同步也具有重要的影响[7].
泄漏电流能引起细胞膜产生超极化,抑制动作电位放电,从而它能够调节pre-Bötzinger复合体中兴奋性神经元及其神经元网络的放电活动,因此泄漏电流对呼吸节律的产生具有重要的作用[8].利用快慢变量分离[9]和双参数分岔分析[10-12]等方法,本文研究了泄漏电导变化对耦合神经元的同相簇同步以及反相簇同步模式的影响.主要内容如下:第一部分介绍pre-Bötzinger复合体中兴奋性神经元模型;第二部分是主要结果,给出泄漏电导变化条件下同相簇同步和反相簇同步的转迁机理;第三部分给出结论.
1 模型描述
本文采用Butera等人于1999年提出的pre-Bötzinger复合体中兴奋性神经元模型[3-4],具体描述如下:
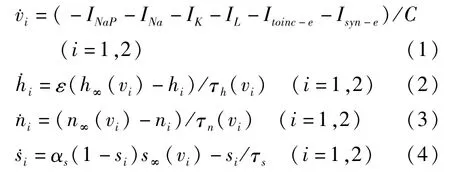

2 耦合神经元簇同步模式及转迁
2.1耦合神经元的快慢动力系统
在pre-Bötzinger复合体的兴奋性神经元模(1)-(4)中,由于ε通常为很小的量,即当v变化时,ε/τh(v)1/τn(v),hi相对其他变量变化慢得多,模型可视为具有快慢系统的动力学模型,其中,快子系统由(1),(3)和(4)组成,慢子系统为(2).hi作为慢变量,可看作快子系统的一个控制参数.本文中我们令gsyn-e=8nS,gtonic-e=0.4nS,此时慢变量h1和h2关于时间t的函数相差很小,如图1⒜,⒝所示.h1和h2关于时间t的轨线完全重合,因此,下文研究中,可令h1=h2=h作为一个慢变量.
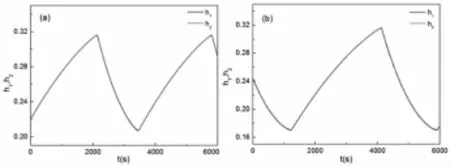
图1 两组初始值下,慢变量h1和h2关于时间t的函数,其中红线代表h1,绿线代表h2⒜初始值:v1=-50mV,v2=-50mV;⒝初始值:v1=-50mV,v2=-60mVFig.1 Plots of h1(red)and h2(green)as functions of time with different initial values⒜Initial values:v1=-50mV,v2=-50mV;⒝Initial values:v1=-50mV,v2=-60mV

图2 不同初始值下膜电位v1和v2关于时间t的变化,其中黑线代表v1,蓝线代表v2⒜v1=-50mV,v2=-50mV,耦合神经元同相同步;⒝a图的部分放大;(c)v1=-50mV,v2=-60mV,耦合神经元反相同步;(d)c图的部分放大Fig.2 Plots of v1(black)and v2(blue)as functions of time with different initial values⒜In-phase synchronization of two-coupled cells with v1=-50mV,v2=-50mV;⒝The enlargement of a part of Fig.⒜;(c)Anti-phase synchronization of two-coupled cells with v1=-50mV,v2=-60mV;⒟The enlargement of a part of Fig.⒞
兴奋性突触连接的耦合神经元的同步模式可表现为同相同步和反相同步,并且对初值具有敏感性[5].本文选取两组不同的初值,在这两组初值下,耦合神经元表现为同相同步与反相同步两种放电模式.如图2所示,图2⒜为同相同步簇放电,图2⒝为2⒜的部分放大图,其中完全同步;图2(c)为反相同步簇放电,图2(d)为2(c)的部分放大图,其中v1,v2反相同步.
2.2耦合神经元双参数分岔分析
在pre-Bötzinger复合体中,泄漏电流对神经元放电过程影响显著,因此,研究泄漏电导变化时呼吸神经元放电模式的影响及其转迁机制有着重要的意义.以慢变量h(h1=h2=h)和漏电导gL作为两个分岔参数,快子系统随这两个参数变化的动力学机制如图3所示.图中的曲线分别表示:超临界Hopf分岔(所指实线suph),亚临界Hopf分岔(实线subh),平衡点的鞍结分岔(实线f1,f2),极限环的鞍结分岔(图⒜中虚线l1和图⒝中虚线l1,l2)和极限环的同宿轨分岔(点线homo).快子系统(1),(3)和(4)(i=1,2)的余维-2分岔点CP,BT和GH分别表示Cusp分岔,Bogdanov-Takens分岔和Bautin分岔.点A,B分别表示同相同步与反相同步平衡点的鞍结分岔曲线(f1)和极限环的鞍结分岔曲线(l1)的交点,点A处gL≈4.54nS,点B处gL≈4.38nS.无论两个耦合神经元表现为同相同步(图3⒜)还是反相同步(图3⒝),快子系统都经历了三个重要的余维-2的分岔点:Cusp分岔(CP),Bogdanov-Takens分岔(BT)和Bautin分岔(GH).
图3⒜表示当耦合神经元同相同步时,单参数分岔曲线(subh,suph,f1,f2,l1和homo)随参数变化的趋势.图3⒝表示当耦合神经元反相同步时,单参数分岔曲线(subh,suph,f1,f2,l1,l2和homo)随参数变化的趋势.其中Cusp分岔是由参数变化时发生在分支f1上的突变“跳跃”到不同平衡点产生的.随参数(gL和h)的增大,超临界Hopf分岔与鞍结分岔同时出现而形成余维-2 Bogdanov-Takens分岔.超临界Hopf岔经由Bautin分岔点变为亚临界Hopf分岔,同时在Bautin分岔点处,极限环的鞍结分岔(l1)产生.
同相同步与反相同步平衡点的分岔结构基本相同,但极限环的分岔不同.与同相同步(图3(a))相比,当耦合神经元反相同步(图3⒝)时,随参数的变化,极限环会产生两种鞍结分岔,即极限环的鞍结分岔l1和l2.下面我们将从这些变化和不同上研究耦合神经元簇同步模式的转迁机理.

图3 快子系统(1),(3)和(4)关于慢变参数h和系统参数gL的双参数分岔⒜耦合神经元同相同步双参数分岔分析;⒝耦合神经元反相同步双参数分岔分析Fig.3 Two-parameter bifurcation of the fast subsystem(1),(3)and(4)with slow variableand h and parameter gL⒜Two-parameter bifurcation analysis for in-phase synchronization of two-coupled cells;⒝Two-parameter bifurcation analysis for anti-phase synchronizationof two-coupled cells
2.3耦合神经元同相簇同步模式及转迁
对两个耦合神经元,给定完全相同的初始条件:v1=-50mV,v2=-50mV,此时耦合神经元表现为同相同步.如图3⒜所示,当0nS<gL<2. 3792nS时,耦合神经元表现为峰放电;当2.3792nS<gL<4.8323nS时,耦合神经元表现为同相簇放电;当gL>4.8323nS时,耦合神经元呈现静息态.图4⒜为gL=3nS时神经元1的簇放电,对应的快子系统(1),(3)和(4)关于慢变量h(h1=h2=h)的分岔如图4⒝所示.在(h,v1)平面上,快子系统的平衡点由三条“S”型曲线组成,其中实线部分代表稳定平衡点,虚线部分代表不稳定平衡点.“S”型曲线上的分岔点(F1,F2,F3和F)代表平衡点的鞍结分岔.在“S”型曲线的上部,当慢变量增加时,不稳定焦点经由亚临界Hopf(subH)分岔变为稳定焦点,同时极限环产生.系统轨线的静息态经由平衡点的鞍结分岔(F1)转变为放电态,放电态又经极限环的同宿轨分岔(HC)转变为静息态,从而形成了一个“fold/homoclinic”型簇放电.
图3⒜中的点A表示同相同步时平衡点的鞍结分岔曲线(f1)和极限环的鞍结分岔曲线(l1)的交点.这意味着随着gL的增大,同相同步平衡点的鞍结分岔(F1)和极限环的鞍结分岔(LPC1)的相对位置将会发生改变.当gL的值大于4.54nS(A点gL≈4.54nS处)时,耦合神经元的簇放电模式发生改变.当,神经元1的簇放电如图5⒜所示,与时“fold/homoclinic”型簇放电完全不同.簇放电的快慢分岔分析如图5⒝所示,时的“fold/homoclinic”型簇放电完全不同系统轨线的下状态即静息态经由鞍结分岔(F1)跃迁到上状态的稳定焦点,轨线围绕稳定焦点旋转且振幅逐渐减少,最后经由亚临界Hopf(subH)分岔转迁为放电态.因此,这种簇放电模式叫做经由“fold/homoclinic”滞后环的“sub-Hopf/homo-clinic”型簇放电.所以随着的增大,耦合神经元的簇放电模式由“fold/homoclinic”型转变为“subHopf/homoclinic”型.当gL>4.8323nS时,h的零等值线与“S”型曲线的交点转移到了鞍结分岔点F1的下方,所以耦合神经元簇放电转变为静息态.同相簇同步模式的转迁中,平衡点的鞍结(f1)分岔,亚临界Hopf(subh)分岔以及极限环的同宿轨(homo)分岔起着关键作用(图3⒜).

图4 gL=3nS,初始值:v1=-50mV,v2=-50mV⒜耦合神经元中神经元1的簇放电;⒝“fold/homoclinic”型簇放电的快慢变量分析Fig.4 gL=3nS,initial values:v1=-50mV,v2=-50mV⒜Bursting pattern of cell-1 in two-coupled cells⒝Fast/slow decomposition for“fold/homoclinic”type bursting
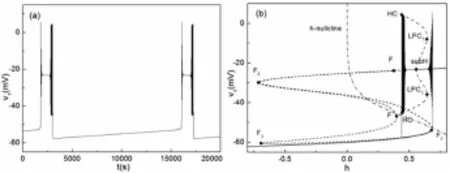
图5 gL=4.8nS,初始值:v1=-50mV,v2=-50mV⒜耦合神经元中神经元1的簇放电;⒝“subHopf/homoclinic”型簇放电的快慢变量分析Fig.5 gL=4.8nS,initial values:v1=-50mV,v2=-50mV⒜Bursting pattern of cell-1 in two-coupled cells;⒝Fast/slow decomposition for“subHopf/homoclinic”type bursting
2.4耦合神经元反相簇同步模式及转迁
当两个耦合神经元的初始条件不同时(v1=-50mV,v2=-60mV),耦合神经元表现为反相同步.如图3⒝所示,当0nS<gL<2.6183nS时,耦合神经元表现峰放电模式;当2.6183nS<gL<4.8323nS时,神经元表现为反相簇放电模式;当gL>4. 8323nS时,耦合神经元呈现静息态.当gL=3nS,神经元1的簇放电如图6⒜所示,其放电模式与同组值下同相簇同步模式不同.如图6⒝所示,神经元静息态经由平衡点的鞍结(F1)分岔转变为峰放电,又由峰放电经极限环的鞍结(LPC2)分岔转变为静息态.因此,这种簇放电叫做“fold/fold cycle”型簇放电.

图6 gL=3nS,初始值:v1=-50mV,v2=-60mV⒜耦合神经元中神经元1的簇放电;⒝“fold/fold cycle”型簇放电的快慢变量分析Fig.6 gL=3nS,initial values:v1=-50mV,v2=-60mV⒜Bursting pattern of cell-1 in two-coupled cells;⒝Fast/slow decomposition for“fold/fold cycle”type bursting

图7 gL=4.8nS,初始值:v1=-50mV,v2=-60mV⒜耦合神经元中神经元1的簇放电⒝“subHopf/fold cycle”型簇放电的快慢变量分析Fig.7 gL=4.8nS,initial values:v1=-50mV,v2=-60mV⒜Bursting pattern of cell-1 in two-coupled cells;⒝Fast/slow decomposition for“subHopf/fold cycle”type bursting
图3⒝中的点B表示反相同步时平衡点的鞍结分岔曲线(f1)和极限环的鞍结分岔曲线(l1)的交点.这意味着随着的增大,反相同步时平衡点的鞍结分岔(F1)与极限环的鞍结分岔(LPC1)的相对位置发生改变.随着gL增大,当gL>4.38nS(B点处gL≈4.386nS)时,耦合神经元反相同步模式发生改变.gL=4.8nS时神经元1的簇放电如图7⒜所示,其相应的分岔分析见图7⒝.神经元静息态经过鞍结分岔(F1)转迁到上状态,在围绕稳定焦点振荡后回到稳定焦点处,稳定态经由亚临界Hopf(subH)分岔转变为放电态,放电态经极限环的鞍结(LPC2)分岔转迁为静息态.因此,这种簇放电称为“subHopf/fold cycle”型簇放电.与神经元同相同步类似,当gL>4.8323nS时,h的零等值线与“S”型曲线的交点转移到了鞍结分岔点F1的下方,所以耦合神经元由簇放电转变为静息态.反相簇同步模式的转迁中,平衡点的鞍结(f1)分岔,亚临界Hopf(subh)分岔以及极限环的鞍结分岔(l2)起到了关键的作用(图3⒝),而极限环的同宿轨(homo)分岔却作用不大.
3 总结
泄漏电流对呼吸节律的产生具有重要的作用,其电流强度的改变会引起呼吸节律的转迁.通过双参数分岔分析和快慢变量分离,我们研究了泄漏电流对耦合神经元簇同步放电模式的影响.结果表明,泄漏电导变化时,同相簇同步模式将从“fold/homoclinic”型转变“subhopf/homoclinic”型;反相簇同步模式将从“fold/fold cycle”型转变为“subhopf/fold cycle”型.耦合神经元不同的簇同步模式及其转迁机制表明同步对呼吸节律的产生和转迁有着重要的影响.本文的研究对进一步探索呼吸节律的产生机制具有一定的意义.
附录:
在本文模型中,对于x∈{mp,m,h,n,s},函数x∞(v)可表示为x∞(v)={1+exp[(v-θx)/σx]}-1.对于x∈{h,n},函数τx(v)可表示为τx(v)=τx/cosh[(v-θx)/2σx].其中所用到的参数的值和单位见表1.

表1 模型中的参数值Table 1 Parameter values in the model
1 Smith J C,Ellenberger H H,Ballanyi K,Richter D W,Feldman J L.Pre-Bötzinger complex:a brain stem region that may generate respiratory rhythm in mammals.Science,1991,254:726~729
2 Rekling J C,Feldman J L.Pre-Bötzinger complex and pacemaker neurons:hypothesized site and kernel for respiratory rhythm generation.Annual Review of Physiology,1998,60(1):385~405
3 Butera R J,Rinzel J,Smith J C.Models of respiratory rhythm generation in the pre-Bötzinger complex.II.Populations of coupled pacemaker neurons.Journal of Neurophysiology,1999,82:398~415
4 Best J,Borisyuk A,Rubin J,Terman D,Wechselberger M.The dynamic range of bursting in a model respiratory pacemaker network.SIAM Journal on Applied Dynamical Systems,2005,4(4):1107~1139
5 Duan L,Zhai D,Tang X.Bursting induced by excitatory synaptic coupling in the pre-Bötzinger complex.International Journal of Bifurcation Chaos,2012,22(05):1250114
6 Gu H G,Li Y Y,Jia B,et al.Parameter-dependent synchronization transition of coupled neurons with co-existing spiking and bursting,Physica A:Statistical Mechanics and its Applications,2013,392(15):3281~3292
7 Gaiteri C,Rubin J E.The interaction of intrinsic dynamics and network topology in determining network burst synchrony.Frontiers in Computational Neuroscience,2011(5):1~10
8 Koizumi H,Smith J C.Persistent Na+and K+-Dominated leak currents contribute to respiratory rhythm generation in the pre-Bötzinger complex in vitro.The Journal of Neuroscience,2008,28(7):1773~1785
9 Rinzel J.Bursting oscillations in an excitable membrane model.In:Sleeman B D,Jarvis R J,eds.Ordinary and partial differential equations.New York:Springer-Verlag,1985:304~316
10 Kuznetsov Y A.Elements of applied bifurcation theory. New York:Springer-Verlag,1995:253~265
11 李群宏,杨丹,闫玉.单向耦合Lorenz Rössler系统的多参数分岔.动力学与控制学报,2013,11(3):203~210(Li Q H,Yang D,Yan Y.Multi parameter bifurcations for the unidirectionally coupled Lorenz Rössler system.Journal Dynamics and Control,2013,11(3):203~210(in Chinese))
BIFURCATION ANALYSIS OF SYNCHRONOUS BURSTING PATTERNS AND TRANSITIONS OF COUPLED NEURONS IN PRE-BÖTZINGER COMPLEX*
Yuan Dandan Chen Xi Duan Lixia†
(College of Science,North China University of Technology,Beijing 100144,China)
The rhythmic bursting of excitatory neurons in the pre-Bötzinger complex is closely related to the respiratory rhythm generation.Leakage current plays an important role in regulating the bursting pattern of neurons. We studied the influences of the leakage current on bursting synchronization and transition mechanisms by both two-parameter bifurcation analysis and fast/slow decomposition.The results show that,under different initial conditions,the coupled cells can exhibit“fold/homoclinic”type and“subHopf/homoclinic”type bursting for inphase synchronization,and exhibit“fold/fold cycle”type and“subHopf/fold cycle”type bursting for anti-phase synchronization.This work provides insights into the study of the respiratory rhythm.
bursting,two-parameter bifurcation,fast/slow decomposition,pre-Bötzinger complex,respiratory rhythm
20 November 2013,revised 17 January 2014.
E-mail:duanlx@ncut.edu.cn
10.6052/1672-6553-2014-015
2013-11-20收到第1稿,2014-01-17收到修改稿.
*国家自然科学基金资助项目(11072013),北京市教委科技计划项目(KM201410009012)
E-mail:duanlx@ncut.edu.cn
*The project supported by the National Natural Science Foundation of China(11072013)and Science and Technology Project of Beijing Municipal Commission of Education(KM201410009012)

