关于Cayley-Hamilton定理的新证明

邓勇



关于Cayley-Hamilton定理的新证明

邓勇

（喀什师范学院 数学系，新疆 喀什 844006）

从形式幂级数和拓扑变换给出凯莱-哈密尔顿定理的2种证法，其中幂级数证明主要是利用多项式的性质，而拓扑证明用到了映射的连续性和矩阵范数.

凯莱-哈密尔顿定理；形式幂级数；拓扑；矩阵；特征值

现今，关于凯莱-哈密尔顿定理的证明已有多种方法，但其证明过程一般较为繁杂，初学者不易掌握[1-3]. 本文从两个新的角度入手，分别应用形式幂级数和拓扑变换的方法，再次证明了凯莱-哈密尔顿定理.

1 幂级数证法

，

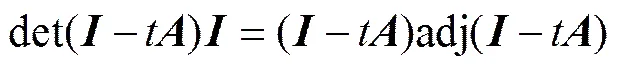
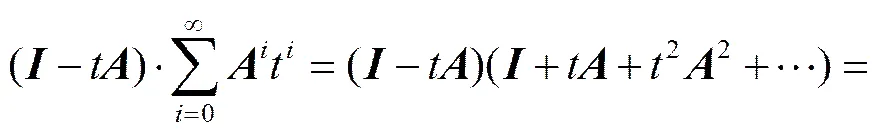
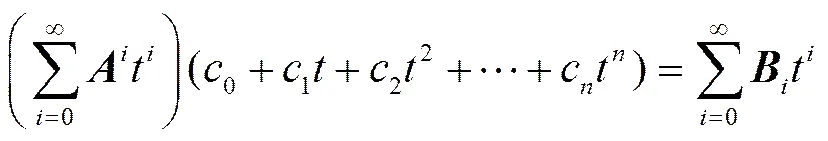
与现有教材和文献提供的证明方法相比，幂级数证法简洁明了，涉及的知识点单一，浅显直观，降低了这部分内容的教学难度，易于初学者理解接受. 因此，建议用幂级数证法替换现有线性代数教材中的相应内容．

2 拓扑学证法

为了得到凯莱-哈密尔顿定理的拓扑学证明，首先介绍2个引理.

.

[1] 张禾瑞，郝鈵新. 高等代数[M]. 5版. 北京：高等教育出版社，2007.

[2] 杨艳，刘合国. Cayley-Hamilton定理的有理证明[J]. 湖北大学学报：自然科学版，2009, 31(2): 109-113.

[3] 刘国新，王正攀. Cayley-Hamilton定理的一个新证明[J]. 西南师范大学学报：自然科学版，2013, 38(8): 1-2.

[4] ABU-SARIS R, AHMAD W. Avoiding eigenvalues in computing matrix powers [J]. The American Mathematical Monthly, 2005, 112: 450-454.

[5] 尤承业. 基础拓扑学讲义[M]. 北京：北京大学出版社，2004: 72.

[6] WILLIAM A, DAVIDSON M G. The Cayley-Hamilton and Frobenius theorems via the Laplace transformation [J]. Linear Algebra and Its Applications, 2003, 371: 147-152.

[责任编辑：熊玉涛]

New Proofs of the Cayley-Hamilton Theorem

DENGYong

(Department of Mathematics, Kashgar Teacher’s College, Kashgar 844006, China)

Two proofs of Cayley-Hamilton theorem are given from the formal power series and the topological transformation. The proof of power series mainly utilizes the quality of the polynomial, and the proof of topology only makes use of the continuity of mapping and matrix norm.

Cayley-Hamilton theorem; formal power series; topology; matrices; eigenvalue

1006-7302（2015）01-0015-03

O151.21

A

2014-06-07

邓勇（1967—），男，四川遂宁人，教授，学士，硕士生导师，主要从事高等代数教学研究.