柔性立管钟型嘴形状参数设计研究

陈柏全，李 英，余建星，程 阳

(天津大学建筑工程学院水利工程仿真与安全国家重点实验室，天津 300072)

柔性立管是海上油气生产系统的重要组成部分，用以连接海底设备和水上诸如FPSO等浮式装置，进行油气输送。由于具有良好的动态特性和可靠性，方便铺设与回收，柔性立管已成为世界上很多油气田开发首选的深水立管型式之一［1］。柔性立管主要的失效模式是疲劳损伤，疲劳损伤最严重的位置通常在立管顶部。柔性立管顶部与浮式结构刚性连接，在静态和动态载荷作用下连接处容易因曲率过大而引起应力集中，进而导致疲劳损伤和破坏，给立管的使用性能造成严重损害［2-5］。

钟型嘴是为保护柔性立管设计和制造的一类弯曲限制器，其作用是限制柔性立管顶端部分的过度弯曲，对于防止柔性立管发生疲劳损伤和破坏起到不可或缺的作用。钟型嘴的形状类似喇叭口，柔性立管从I型管顶端穿入，从钟型嘴底端穿出，如图1所示。在各种载荷作用下柔性立管发生非线性大位移运动，产生弯曲和偏转，钟型嘴能够将柔性立管的弯曲和偏转限定在允许范围内，进而很好地保护柔性立管。

钟型嘴的设计基于柔性立管悬挂点的最大偏转角φm和最小允许弯曲半径(MBR)。最大偏转角φm通过开展所有设计工况下的整体分析计算得到，MBR由立管的性质所决定。最简单的钟型嘴形状是在其长度范围内保持恒定的弯曲半径，然而这种形状会使钟型嘴顶端与立管的接触力过大，而底端与立管的接触力很小甚至不与立管接触，这对于柔性立管的疲劳性能不利。应在钟型嘴的顶部提供比较大的弯曲半径，在底部提供相对较小的弯曲半径［6］。这样，在一般海况条件下立管会与钟型嘴顶部有规律地发生接触，而只有在极端海况条件下才会与钟型嘴底部发生接触。国外在钟型嘴等立管附件的设计、制造和测试等方面已有多年经验，而国内在这一领域的研究几乎属于空白［7-8］。规范API RP 17B［6］提出曲率与弧长成线性关系的钟型嘴形状，在国内外的科研及工程实际中被普遍采用［9-12］。宋夏［7］运用ABAQUS有限元分析软件对4种不同形状的钟型嘴进行比较分析，通过对比柔性立管接触应力得出当曲率与弧长成线性关系时钟型嘴综合性能最好的结论。

在工程中，钟型嘴的设计要求在能够有效限制柔性立管过度弯曲进而避免应力集中的前提下，尽可能地减小钟型嘴的体积和质量。钟型嘴体积减小和质量减轻具有重要意义:1)节约材料，节省成本，利于钟型嘴的安装;2)便于柔性立管的布置，在布置同样数量柔性立管的情况下，增大了柔性立管之间的空间，减小了柔性立管之间碰撞的可能性。文中针对位于350 m水深的某油田一根柔性立管设计案例，基于规范API RP 17B中的钟型嘴形状，根据上述设计要求对钟型嘴几何形状进行优化。基于预期钟性嘴体积较小且曲率与弧长函数关系不太复杂的考虑，提出以下两种优化方案:1)钟型嘴曲率与弧长的平方根成线性关系;2)由于对数函数在弧长为零时无意义，钟型嘴曲率与弧长成分段函数关系(线性关系和对数关系)。通过分析对比不同方案中钟型嘴的弧长及质量、柔性立管顶端部分的曲率、柔性立管与钟型嘴的接触力以及柔性立管顶端部分的有效张力，对优化方案进行综合评估。

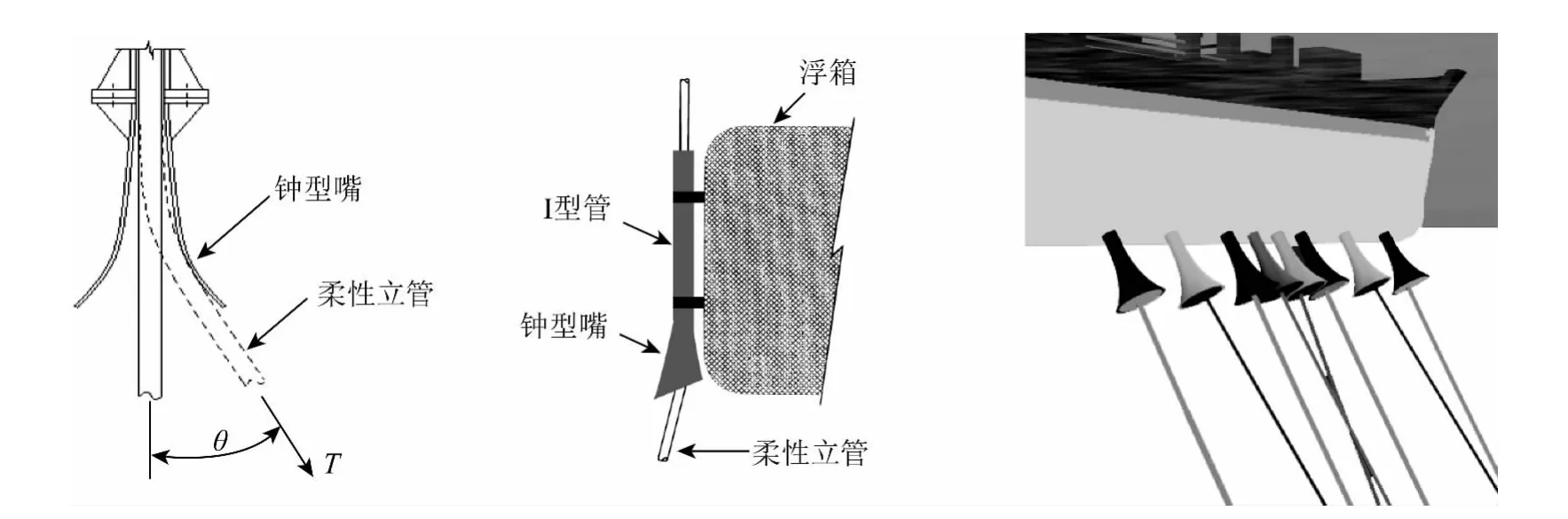
图1 钟型嘴与柔性立管(左)、平台(中)及FPSO(右)的连接Fig.1 Connection between bellmouth and flexible riser(left)，platform(middle)，and FPSO(right)

1 钟型嘴的几何公式

1.1 钟型嘴的相关参数

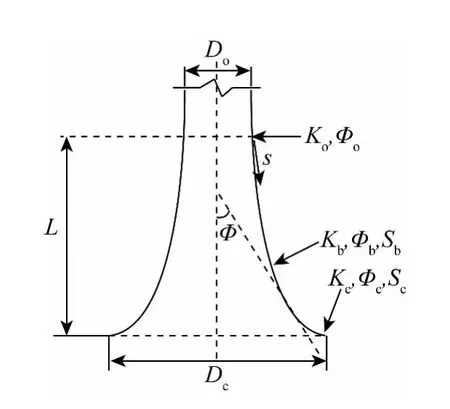
图2 钟型嘴剖面示意Fig.2 Sketch map of bellmouth

钟型嘴的剖面示意及相关参数如图2所示。其中，D0为钟型嘴顶端内径;Dc为钟型嘴底端内径;s为钟型嘴剖面弧长;φ为钟型嘴剖面上某点的切线角;L为钟型嘴中轴长;K0，Kb，Kc分别为钟型嘴剖面顶端、中间某点、底端的曲率;φ0，φb，φc分别为钟型嘴剖面顶端、中间某点、底端的切线角;sb，sc分别为钟型嘴剖面上中间某点、底端的弧长。钟型嘴的形状由顶端曲率K0、顶端切线角φ0、底端曲率Kc、底端切线角φc以及顶端内径D0五个边界参数确定。其中，K0影响钟型嘴的形状变化及开口大小，为了与I型管平滑连接，K0一般取较小值，这里取0.001;φ0影响钟型嘴的开口大小，为了与I型管平滑连接，φ0一般取0°;K影响钟型嘴弧长、形状变化及开口大小，根据柔性立管的MBR确定，并且Kc=1/RMBR;φc影响钟型嘴弧长及开口大小，根据柔性立管悬挂点的最大偏转角φm确定，并且φc至少比φm大5°［6］。D0影响钟型嘴的开口大小，根据柔性立管的外径D确定，若D0过大，则钟型嘴的限制弯曲效果变弱，若D0过小，则会造成立管顶端预紧力过大，容易导致柔性立管端部应力集中［7］，文中取D0比 D大0.01 m。

1.2 钟型嘴几何公式的推导

钟型嘴几何公式的推导分为三个部分:1)钟型嘴的曲率随弧长变化的关系式;2)钟型嘴的切线角随弧长变化的关系式;3)钟型嘴底端弧长的确定式。将钟型嘴曲率、切线角随弧长变化的关系式转化为直角坐标系下中轴长与剖面半径的关系式，进而确定钟型嘴的剖面形状。基于规范API RP 17B中曲率与弧长成线性关系的钟型嘴几何形状，提出钟型嘴曲率与弧长的平方根成线性关系(优化方案一)以及钟型嘴曲率与弧长成分段函数关系(线性关系和对数关系，优化方案二)两种优化方案，以下为各方案钟型嘴几何公式的推导过程。

1.2.1 规范方案

在规范API RP 17B中，假设钟型嘴曲率与弧长成线性关系，即

在钟型嘴顶端，有 K0、φ0=0、s0=0;在钟型嘴底端，有 Kc、φc、sc。令

得到

将式(3)和(4)代入式(1)，得到

由角度和曲率的关系确定sc，有

将式(5)代入式(6)，计算得到

将式(7)代入式(5)，最终得到曲率与弧长成线性关系的钟型嘴几何公式:

1.2.2 优化方案一

假设钟型嘴曲率与弧长的平方根成线性关系，即

同理可推导得到钟型嘴的几何公式如下

1.2.3 优化方案二

将钟型嘴分为两部分:第一部分，弧长0～sb，该部分的形状与规范方案的形状相同;第二部分，弧长sb～sc，该部分钟型嘴的曲率与弧长的自然对数成线性关系。即

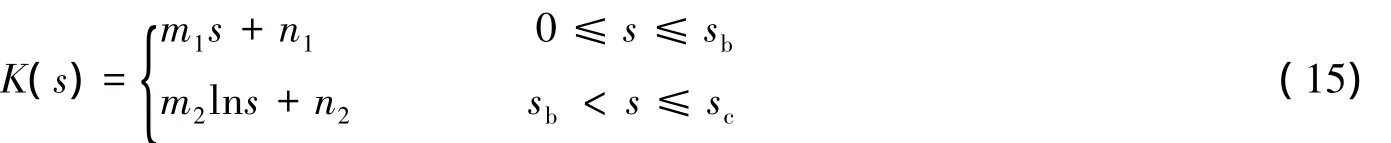
在该优化方案中，sb可以有不同的取值，进而得到不同的剖面形状。同理可推导得到钟型嘴的几何公式。

弧长0～sb部分:

弧长sb～sc部分:

式中:γ=Kb/Kc。

2 弧长及质量评估

以某350 m水深油田柔性立管设计为案例，进行柔性立管钟形嘴几何形状的优化设计。海况条件如表1所示，柔性立管的相关参数如表2所示。

手机端联机或脱机，闸机端处于脱机状态，采用信用消费方式，手机端生成二维码，进出站后二维码不刷新进出站状态，后台对进出站交易配对。容易产生单边交易，配对不成功，造成票款损失。西安、无锡、福州、南昌、大连、苏州采用这种方式。

表1 波浪和海流参数Tab.1 Wave and current parameters

表2 柔性立管参数Tab.2 Flexible riser parameters

根据钟型嘴的形状公式确定钟型嘴的剖面，图3给出了规范方案和优化方案的剖面图，其中优化方案二取sb=0.5 m、1.0 m、1.5 m三种情况。由图3可以看出:1)优化方案钟型嘴的中轴总长均小于规范方案，其中优化方案一为2.927 m，优化方案二中sb=0.5 m时为3.260 m，sb=1.0 m时为3.594 m，sb=1.5 m时为3.775 m，而规范方案为3.953 m;2)在中轴长相同的位置，优化方案的钟型嘴开口均大于规范方案;3)随着sb取值减小，优化方案二的钟型嘴形状越来越接近优化方案一;随着sb取值增大，优化方案二的钟型嘴形状越来越接近规范方案。

图3 几种方案下钟型嘴剖面图Fig.3 Profile map of bellmouth

钟型嘴厚度为0.05 m，材料密度为7.8×103kg/m3，经计算得到各类形状钟型嘴的弧长和质量，对比结果如表3所示。由表3可以看出:1)钟型嘴的质量与弧长之间有密切关系，所有优化方案钟型嘴的弧长和质量均小于规范方案，其中优化方案一的最小，优化方案一与规范方案相比弧长减小了24.9%，质量减小了24.1%;2)对于优化方案二，由于随着sb取值增大钟型嘴的形状越来越接近规范方案，钟型嘴弧长和质量的减小量也相应地变小。

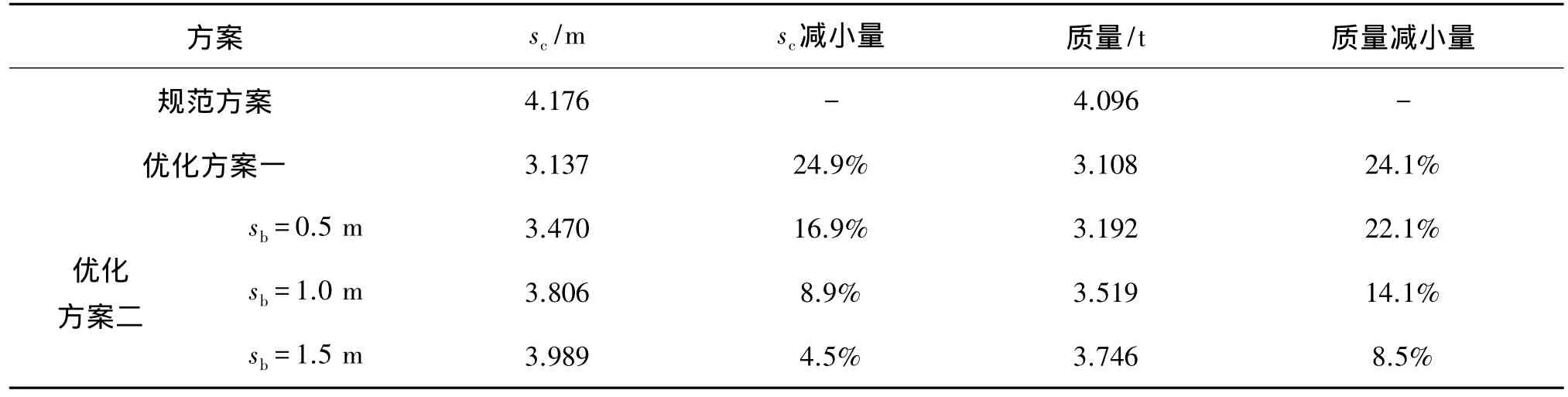
表3 钟型嘴弧长和质量对比Tab.3 Comparison of arc length and mass of bellmouth

3 水动力分析

3.1 模型建立

利用OrcaFlex软件建立有限元模型，对比分析各方案中柔性立管顶端部分的曲率、柔性立管与钟型嘴的接触力以及柔性立管顶端部分的有效张力，以检验优化后的钟型嘴是否满足限制柔性立管过度弯曲进而避免柔性立管应力集中的性能要求。

图4为有限元模型全局图和局部放大图，钟型嘴顶端连接2 m长的I型管，I型管顶端固定在FPSO上。根据钟型嘴和I型管的几何形状，建立接触模型。柔性立管采用陡波型(steep wave)线型，立管穿过I型管和钟型嘴内部，顶端与FPSO连接，底端锚固在泥面上的井口处。柔性立管顶端部分10 m范围内的单元长度划分为0.1 m，其余部分单元长度为0.2 m。采用规则波进行动力分析，运用时域分析方法计算立管的动力响应。

3.2 动力响应结果分析

3.2.1 柔性立管顶端部分的曲率

不同设计方案中，柔性立管顶端部分最大曲率沿立管弧长的分布曲线如图5所示。

由图5可以看出:1)优化方案出现最大曲率的位置比规范方案更加靠近钟型嘴顶端，优化方案一出现最大曲率的位置位于距离钟型嘴顶端0.75 m处，规范方案出现最大曲率的位置位于距离钟型嘴顶端1.45 m处，优化方案二介于两者之间，随着sb增大，优化方案二出现最大曲率的位置向规范方案靠近，当sb=1.5 m时优化方案二的曲率分布曲线与规范方案几乎重合;2)sb=0.5 m时的优化方案二的曲率值最大，为0.083 7 m-1，规范方案的曲率值最小，为0.076 8 m-1，二者均远小于柔性立管所允许的最大曲率0.333 3 m-1，说明各类形状钟型嘴都对柔性立管的弯曲起到很好限制作用，优化后的钟型嘴满足限制柔性立管过度弯曲进而避免应力集中的性能要求。

图4 模型全局图和局部放大图Fig.4 Model global graph and partially enlarged detail

图5 柔性立管顶端部分的曲率对比Fig.5 Comparison of curvature at the top of flexible riser

不同设计方案中，柔性立管与钟型嘴最大接触力沿立管弧长的分布曲线如图6所示。

从图6可以看出:1)优化方案出现最大接触力的位置比规范方案更加靠近钟型嘴顶端，优化方案一出现最大接触力的位置位于距离钟型嘴顶端0.8 m处，规范方案出现最大接触力的位置位于距离钟型嘴顶端1.6 m处，优化方案二介于两者之间，随着sb增大，优化方案二出现最大接触力的位置向规范方案靠近;2)sb=0.5 m时的优化方案二的最大接触力值最大，为16.36 kN，规范方案的最大接触力值最小，为13.61 kN，最大值与最小值之间相差2.75 kN，其它方案介于二者之间，上述接触力值之间相差不大，进而单位面积上的应力相差也较小，对柔性立管的强度和疲劳破坏没有太大的影响。

3.2.3 柔性立管顶端部分的有效张力

不同设计方案中，柔性立管顶端部分的有效张力沿立管弧长的分布曲线如图7所示。

从图7可以看出:优化方案与规范方案对比，柔性立管顶端部分的有效张力的大小及范围几乎一致，虽然在距离钟型嘴顶端0.4～2.2 m的范围内出现微小的偏差，但是最大张力均为124 kN，对整体结构的影响几乎没有差别。

图6 柔性立管与钟型嘴的最大接触力沿立管弧长分布Fig.6 Contact force between flexible riser and bellmouth along the flexible riser

图7 柔性立管顶端部分的有效张力对比Fig.7 Comparison of effective tension at the top of flexible riser

综合上述结果表明，优化后的钟型嘴均能够满足限制柔性立管过度弯曲进而避免柔性立管应力集中的性能要求。

4 结语

提出两种优化方案对规范API RP 17B中的钟型嘴几何形状进行优化，推导总结了各方案的几何公式，并将优化方案与规范方案进行对比分析。首先对比各形状钟型嘴的弧长和质量，再利用OrcaFlex软件建立有限元模型对比分析各形状钟型嘴的性能是否满足设计要求。弧长和质量方面，所有优化方案钟型嘴的弧长和质量均小于规范方案，其中优化方案一的弧长和质量最小;柔性立管顶端部分的曲率方面，所有方案的钟型嘴对柔性立管的弯曲都起到很好限制作用;柔性立管与钟型嘴的接触力方面，优化方案的接触力比规范方案的接触力略大，但不会对柔性立管疲劳破坏产生过大的影响;柔性立管顶端部分的有效张力方面，有效张力的大小及范围几乎一致。文中所提出的优化方案为钟型嘴的设计和制造提供了参考和选择，在工程实践中可以根据结构质量、受力等设计目标和海况条件等相关因素选择最合适的钟型嘴形状。

［1］ CORRIGNAN H，RAMOS R T，SMITH R，et al.New monitoring technology for detection of flexible armour wire failure［C］//Offshore Technology Conference.2009.

［2］ PIPA D，MORIKAWA S，PIRES G，et al.Flexible riser monitoring using hybrid magnetic/optical strain gage techniques through RLS adaptive filtering［J］.EURASIP Journal on Advances in Signal Processing，2010:doi:10.1155/2010/176203.

［3］ BAI Yong，BAI Qiang.Subsea pipelines and risers［M］.2nd Revised Edition，Elsevier Science Ltd.，2005:501-502.

［4］ CAIRE M，VAZ M A.The effect of flexible pipe non-linear bending stiffness behavior on bend stiffeneranalysis［C］//Proceedings of 26th International Conference on Offshore Mechanics and Arctic Engineering，ASME.American Society of Mechanical Engineers，2007:103-109.

［5］ 李彤，李鹏，张鸿凯，等.柔性立管防弯器的设计［J］.中国造船，2010，51(2):168-173.(LI Tong，LI Peng，ZHANG Hongkai，et al.A design method on bending stiffener of flexible risers［J］.Shipbuilding of China，2010，51(2):168-173.(in Chinese))

［6］ API RP 17B，Recommended practice for flexible pipe［S］.2002:58-59.

［7］ 宋夏.柔性立管钟型嘴设计及分析［D］.上海:上海交通大学，2012.(SONG Xia.Design and analysis of bellmouth in flexible riser［D］.Shanghai:Shanghai Jiao Tong University，2012.(in Chinese))

［8］ 李博.海洋动态柔性立管附件设计与分析［D］.大连:大连理工大学，2011.(LI Bo.Design and analysis for accessories of marine dynamic flexible riser［D］.Dalian:Dalian University of Technology，2011.(in Chinese))

［9］ FONTAINE E，HEURITER J M，DURVILLE D，et al.Modeling of riser contact-friction problems［C］//Offshore Technology Conference.2002:OTC-14157-MS.

［10］ SæVIK S.Comparison between theoretical and experimental flexible pipe bending stresses［C］//Proceedings of 29th International Conference on Ocean，Offshore and Arctic Engineering，ASME.American Society of Mechanical Engineers，2010:395-402.

［11］ SæVIK S.Theoretical and experimental studies of stresses in flexible pipes［J］.Computers ＆ Structures，2011，89(23):2273-2291.

［12］ RUSTAD A M，SODAHL N，KALLEKLEV A J，et al.Use of weight elements to improve the dynamic performance of umbilicals［C］//Proceedings of 29th International Conference on Ocean，Offshore and Arctic Engineering，ASME.American Society of Mechanical Engineers，2010:171-175.