粗粒土级配及颗粒破碎分形特性

陈镠芬，高庄平，朱俊高，殷建华



粗粒土级配及颗粒破碎分形特性

陈镠芬1, 2，高庄平1，朱俊高1, 2，殷建华3

(1. 河海大学岩土力学与堤坝工程教育部重点实验室，江苏南京，210098；2. 河海大学岩土工程科学研究所，江苏南京，210098；3. 香港理工大学土木工程系，香港，999077)

验证颗粒质量−粒径分布分形模型用于表示粗粒土级配的适用性，研究粗粒土在不同缩尺粒径的情况下，采用不同缩尺方法缩尺后土体分形维数的变化规律；基于分形维数建立缩尺级配与原始级配之间的联系，分析不同母岩材料、级配和颗粒形状粗粒土三轴试验资料，推算粗粒土的相对破碎率，并探讨分形维数与相对破碎率的关系。研究结果表明：分形维数能定量描述粗粒土的原始级配和缩尺级配，不同缩尺方法得到的粒度分形曲线形态有较大差别，与原始级配的粒度分形曲线有不同程度的偏离，缩尺粒径越小偏离程度越大。在所研究的4种缩尺方法中，分形维数与缩尺粒径的对数呈较好的线性关系；围压越大，破碎分形维数和相对破碎率越大，试验前粗粒土的分形维数越大，剪切试验后相对颗粒破碎率越小。不同母岩、级配和颗粒形状的破碎分形维数与相对破碎率呈幂函数关系，通过分形维数和拟合参数可估算不同围压下的相对破碎率。

粗粒土；级配；颗粒破碎；分形维数；相对破碎率

粗粒土是指直径大于5 mm颗粒的质量分数超过50%的卵、砾石料或堆石料，其在较高的压力下易破碎，颗粒破碎现象在高土石坝中尤其值得关注。颗粒破碎引起土体级配的改变，从而改变粗粒料的物理力学性质。然而，如何描述破碎前后级配的差异，一直是一个难题，相关研究较多，但多不理想。实际上，若能找到准确描述级配的数学描述，颗粒破碎定量表述就较容易实现。因此，研究粗粒土颗粒破碎程度，首先需要解决级配的准确表述问题。对粗粒土，级配是影响其物理力学性质的重要因素，颗粒破碎引起级配变化，从而导致其力学性质变化，然而，迄今为止，级配的准确定量描述仍依赖于级配曲线。虽然不均匀系数及曲率系数能在一定程度上反映级配，但并不准确。已有学者利用分形理论研究土体级配，但多针对细粒土的研究，对于粗粒土研究较少，因此，粗粒土级配的定量表述方法值得深入研究。关于颗粒破碎，国内外学者分别从试验、理论及数值计算方法等方面进行研究，涉及颗粒破碎对土体工程特性影响[1−2]、颗粒破碎度量及影响因素[3−4]和考虑颗粒破碎的本构模型[5−7]这3方面。自20世纪80年代以来，谢和平 等[4, 8−9]采用分形理论对细粒土进行深入研究，研究结果表明：由形状与大小各异的岩土体颗粒和孔隙组成的材料都存在自相似性，都具有分形特性。对于粗粒土，现有研究成果亦表明[10−11]，在不同的粒度范围内粗粒土都表现出一定的分形特征。分形维数作为分形理论的研究手段，已成为研究岩土材料物理力学性质的一个重要指标。本文作者基于几种土石坝粗粒料的设计级配，研究分形模型对粗粒土级配的适用性，并对双江口堆石坝的坝壳堆石料采用不同缩尺方法缩尺后粗粒土的级配分形维数的差异进行比较，建立不同缩尺方法缩尺后级配与原型级配的内在联系；对多种堆石料大型三轴试验资料进行分析，研究试验前后的粒径分布，推算堆石料的相对破碎率，从而探讨分形维数与相对破碎率之间的关系，分析试验引起的颗粒破碎情况及分形维数的变化。

1 质量−粒径分形模型对粗粒土级配适用性验证

自分形理论应用于岩土体以来，学者提出许多岩土体颗粒或孔隙的分形模型，并在此基础上研究岩土体的孔隙率、非饱和土的水分特征曲线、渗透性和土体抗剪强度等，取得较好的成果[12−13]。适合粗粒土级配的分形模型包括粒径−数量分形模型和质量−粒径分形模型，鉴于粒径−数量关系较难从试验直接获得，对于粗粒土的分形特性研究一般采用颗粒质量−粒径分形模型[14]，即

对式(1)两边取对数得

为验证所选用的分形模型对粗粒土的适用性，整理双江口、长河坝、糯扎渡及小浪底等心墙堆石坝的4种堆石料原始级配粒度分形曲线，即关系曲线，如图1所示。由图1可以看出：它们之间表现出良好的线性关系，因此，用式(2)拟合，可求得分形维数，表1所示为相应的分形维数和线性拟合的相关系数。

由图1和表1可以看出：不同堆石料原始级配的粒度分形曲线呈显著的线性关系，相关系数2均超过0.99，表明本文所选取的分形模型能较好地反映堆石料的分形特性。这几种堆石料的分形维数在2.456~2.577，分布在一个狭窄的区间内。

1—双江口；2—长河坝；3—糯扎渡；4—小浪底

表1 不同堆石料原始级配的分形维数及相关系数

2 缩尺方法对分形维数的影响

土石坝的堆石料原始级配具有显著分形特性，但在室内试验时，颗粒粒径会受到试验仪器的限制，一般需要将堆石料的原始级配进行缩尺，而缩尺方法、最大缩尺粒径会使粗、细颗粒质量分数发生改变，引起级配曲线形态的差异。缩尺后是否还能用分形维数描述级配值得研究。本节重点研究双江口堆石坝的坝壳堆石料级配缩尺后的分形特性，其他几种堆石料的规律一致。

土工试验中常用的缩尺方法为剔除法、等量替代法、相似级配法和混合法，对应符号依次用T，E，X和H表示，采用的最大缩尺颗粒直径M(以下称缩尺粒径)为60和20 mm。如剔除法，缩尺粒径为60和20 mm的编号为T60和T20，其余缩尺方法的编号方法类似。双江口堆石料的原始级配及缩尺级配曲线如图2所示，相应的粒度分形曲线及分形维数如图3和表2所示。

从图2和图3可以看出：不同缩尺方法下的级配曲线和粒度分形曲线与原始曲线都有较大不同。相似级配法缩尺后各粒组之间相对质量分数和填充关系不发生变化，级配良好，粒度分形曲线与原始曲线重合，线性相关性较好；剔除法和等量替代法缩尺后级配曲线和粒度分形曲线都存在突变部分，突变点随着缩尺粒径的变化而不同，级配不良，粒度分形曲线线性相关性较差；混合法的级配曲线和粒度分形曲线介于等量替代法与剔除法之间，级配较好，线性相关性较好。由此可知：级配曲线和粒度分形曲线是相对应的，进一步证明可以通过分形维数来描述级配曲线。

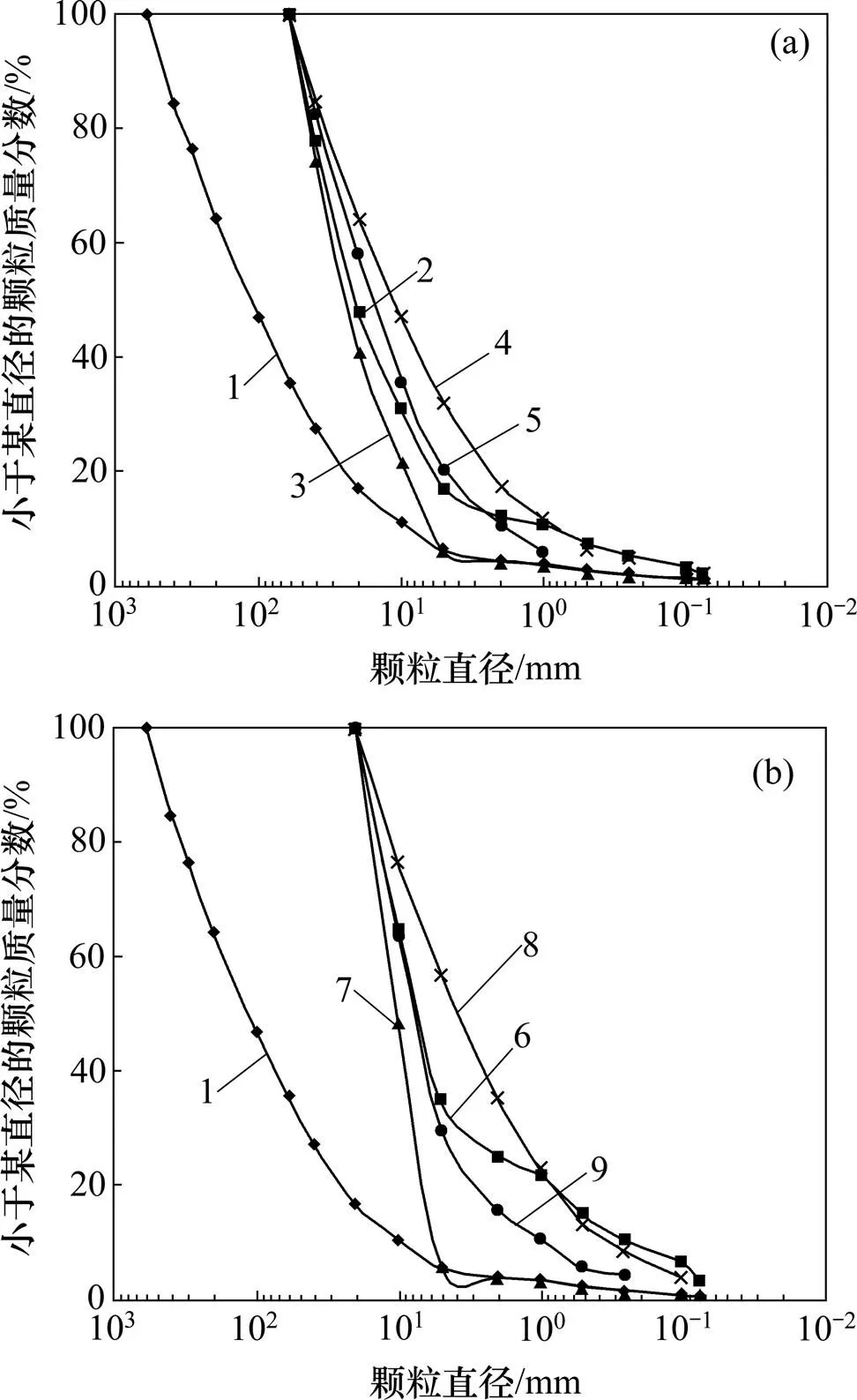
dM/mm: (a) 60; (b) 20 1—原始级配；2—T60；3—E60；4—X60；5—H60；6—T20；7—E20；8—X20；9—H20

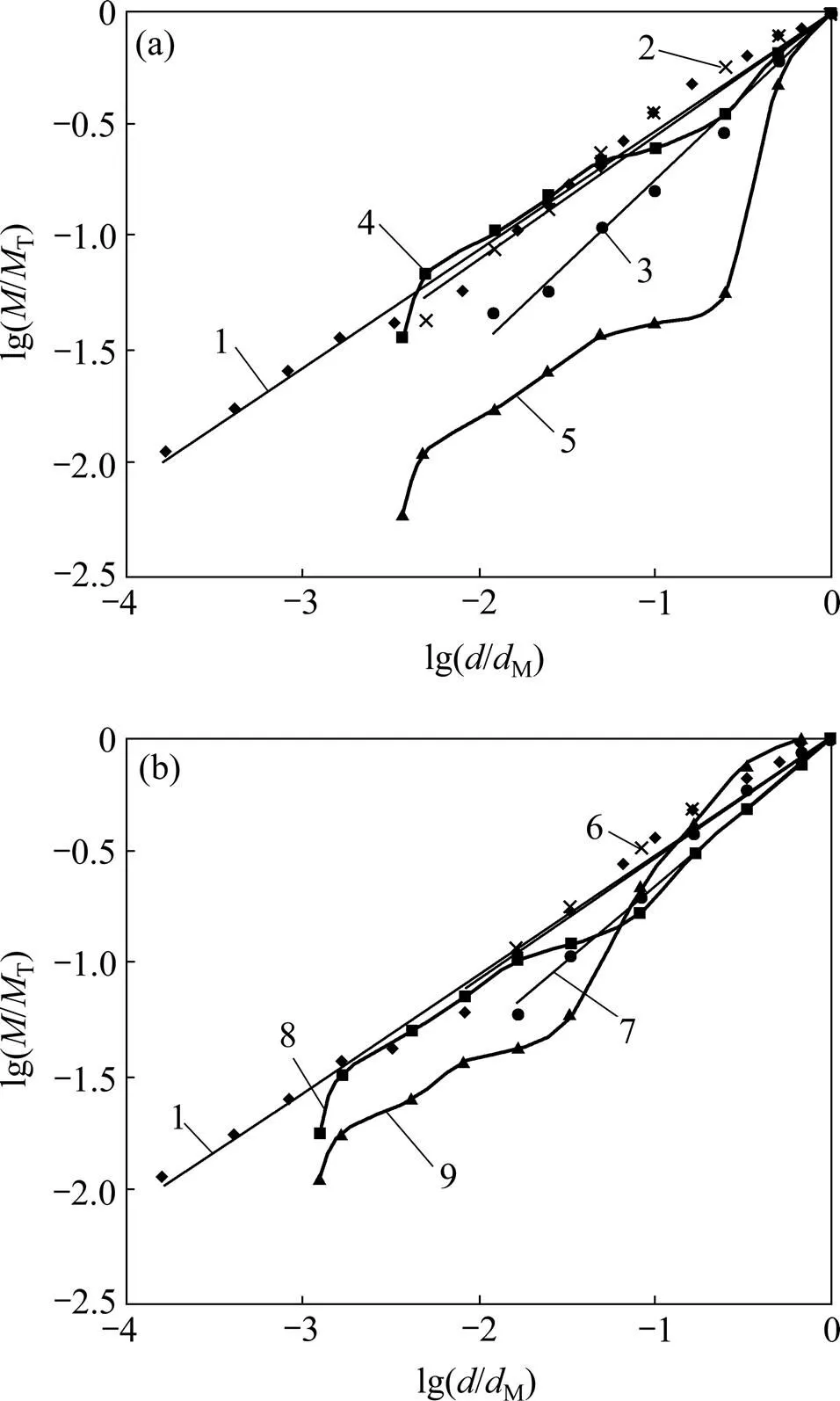
dM/mm: (a) 60; (b) 20 1—原始级配；2—X20；3—H20；4—T20；5—E20；6—X60；7—H60；8—T60；9—E60

另外，根据图3中不同缩尺粒径的粒度分形曲线分布情况，缩尺后粒度分形曲线与原始粒度分形曲线有一定程度的偏离，缩尺粒径愈小则偏离越大。对于同一缩尺粒径，等量替代法的粒度分形曲线偏离原始级配最大，剔除法的粒度分形曲线靠近原始级配，混合法的粒度分形曲线介于等量替代法与剔除法之间。理论上采用相似级配法缩尺得到的级配分形维数与原级配一致，但由于级配宽度及缩尺粒径的变化，实际拟合过程会有所不同，如表2所示。

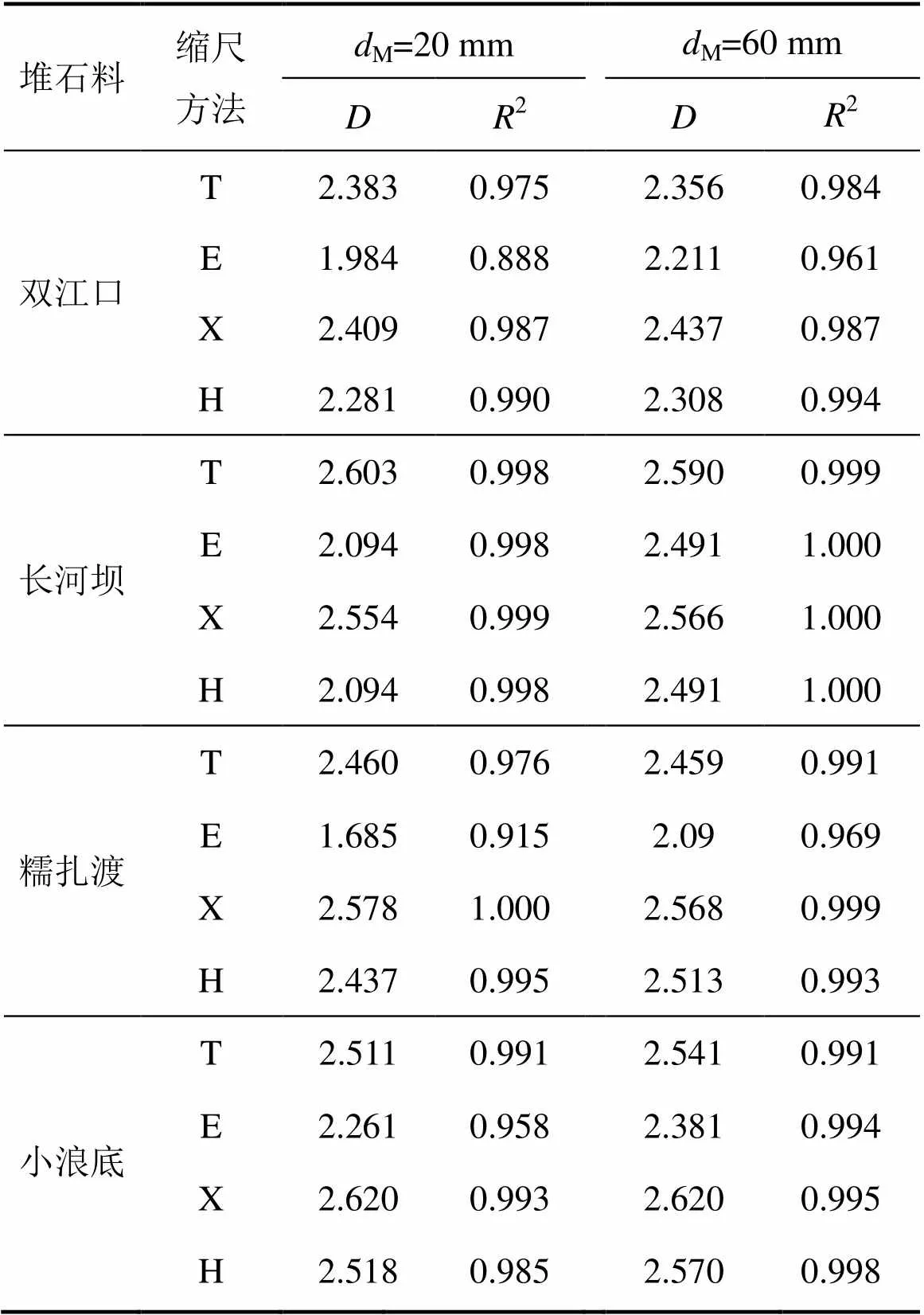
表2 不同堆石料不同缩尺方法的分形维数

从表2可以看出：与另外3种缩尺方法相比，等量替代法的粒度分形曲线线性相关性较差，而其余缩尺方法的粒度分形曲线线性相关性较好，属于严格自相似。但随着缩尺粒径的增加，等量替代法的粒度分形曲线线性相关系数有一定提高，这与其粒度分形曲线吻合。因此，对于大缩尺粒径的等量替代法及另外3种缩尺方法都能用分形维数来描述级配。级配缩尺后，堆石料分形维数的变化范围变大，在1.685~2.603之间，且分形维数总体上随着缩尺粒径的增大而增大。

为了表述缩尺方法引起的分形维数差异及缩尺前后分形维数的内在联系，本文作者取缩尺粒径的对数为横坐标，分形维数为纵坐标，建立各缩尺粒径和分形维数的关系曲线，以双江口为代表，如图4所示。

从图4可以看出：缩尺粒径与分形维数呈较好的线性关系，相关系数2=0.906~0.969。分形维数随着缩尺粒径的增大而增大，且随着缩尺粒径的增大，各缩尺方法的分形维数也越来越相近，同时也越靠近原始级配的分形维数，即缩尺粒径越大越靠近原型级配，其物理力学特性表现越接近实际情况。

缩尺方法：1—T；2—E；3—X；4—H

3 颗粒破碎的分形特性

上述研究表明：对级配连续的粗粒土，分形维数能够较好地描述其级配，因而本文作者从分形维数的角度研究级配与颗粒破碎的相互联系。在大粒径三轴试验中，粗颗粒通常与邻近颗粒有较多接触，颗粒间产生较多力链，产生颗粒破碎概率较高；而细颗粒与邻近颗粒接触较少，甚至是悬浮在粗颗粒间，受力较小，产生颗粒破碎概率较低，因此，本文仅考虑粗颗粒的颗粒破碎。

首先对文献[3, 16]中不同母岩、不同级配及不同颗粒形状的粗粒土大三轴试验资料进行整理，根据不同围压(300，600，700，800，900，1 200和1 600 kPa)下试验前及剪切后(以试样轴向应变达到15%为试验终止条件)级配的变化研究分形维数和颗粒破碎率r之间的关系。为区别颗粒破碎前后级配的分形维数，将颗粒破碎后级配的分形维数称为破碎分形维数，记为2，破碎前的分形维数记为1，如表3所示。图5所示为石英砂岩在试验后的粒度分形曲线。

由图5可以看出：颗粒破碎前后的粒度分形曲线有较大差别，围压越大，粒度分形曲线拟合直线的斜率越小，相关系数2为0.974~0.991，表明颗粒破碎后粒径分布的分形特性仍显著，采用分形维数研究颗粒破碎这种方法可行。

由表3可以看出：围压越大，破碎分形维数越大。对于饱和单轴抗压强度较大的堆石料(如石英砂岩、片麻岩和砂砾岩)，破碎导致分形维数增加幅度减小，而对于饱和单轴抗压强度较小的堆石料(砂板岩)或是多棱角的堆石料(灰岩)，破碎使分形维数增加幅度增大。

围压/kPa：1—试验前；2—200；3—600；4—900；5—1 200

表3 不同围压下各粗粒土的分形维数和相对破碎率

越来越多的研究表明，颗粒材料在荷载作用下颗粒破碎最终会趋于稳定，级配曲线会达到一个分形分布。Einav[17]在Hardin破碎理论的基础上引入分形理论，提出基于分形理论的修正Hardin破碎指标r(如图6所示)，其定义如下：

式中：()，0()和u()分别为以颗粒质量表示的当前、初始和极限颗粒级配曲线函数；m和M分别为试样最小和最大直径。图6中，p表示破碎势，横坐标代表试样直径。

基于分形模型，u()的表达式为：

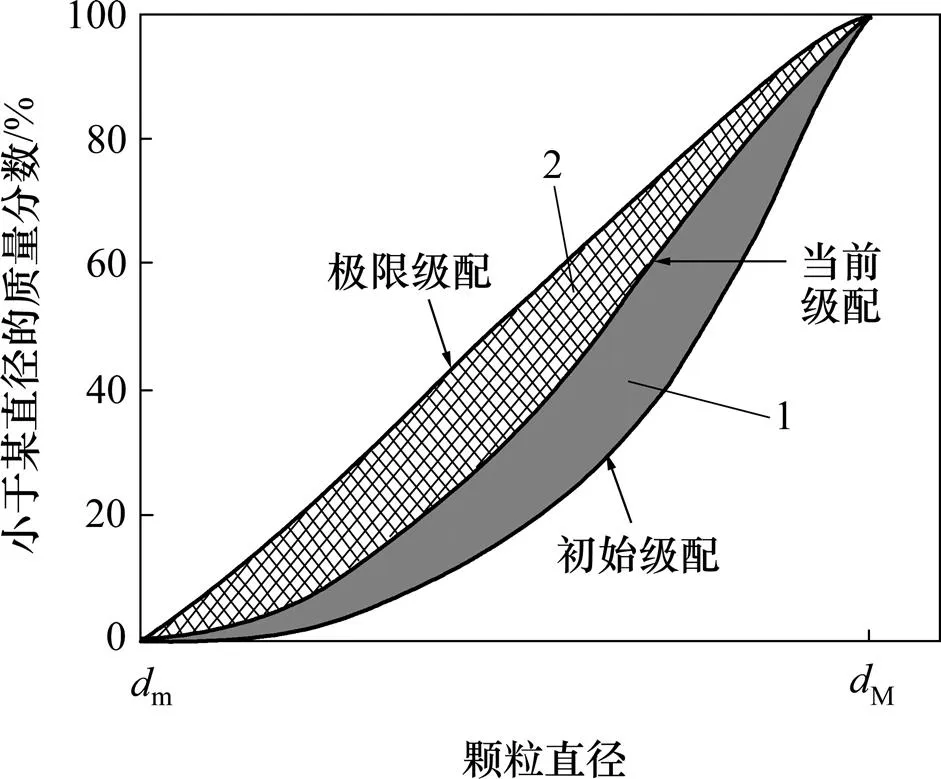
1—Br; 2—Bp

修正相对破碎率r是材料的一种基本属性，反映土体总体破碎情况，计算方便及物理意义明确，因此，本文作者采用此指标研究其与分形维数之间的内在联系，通过分形维数和式(3)计算的相对破碎率如表3中r所示。

从表3可看出：围压越大，相对破碎率越大，破碎分形维数变化越大，相对破碎率变化也越大。试验前粗粒土的分形维数越大，试验后颗粒相对破碎率就越小。分形维数大，则细粒较多，细粒能很好地填充孔隙，从而使粗粒与其他颗粒接触变多，颗粒破碎量小，反之亦然。因而可以将分形维数作为颗粒破碎量化指标，来推算不同级配粗粒土在各围压下的颗粒破碎程度。

为了反映粗粒土破碎前后分形维数、围压和相对破碎率之间的变化规律，总结这几方面因素的相互关系如下：

1) 对破碎前后分形维数1，2和围压进行整理，以2/1为横坐标，/a为纵坐标绘制曲线，并作线性回归分析，a为大气压强，如图7所示。

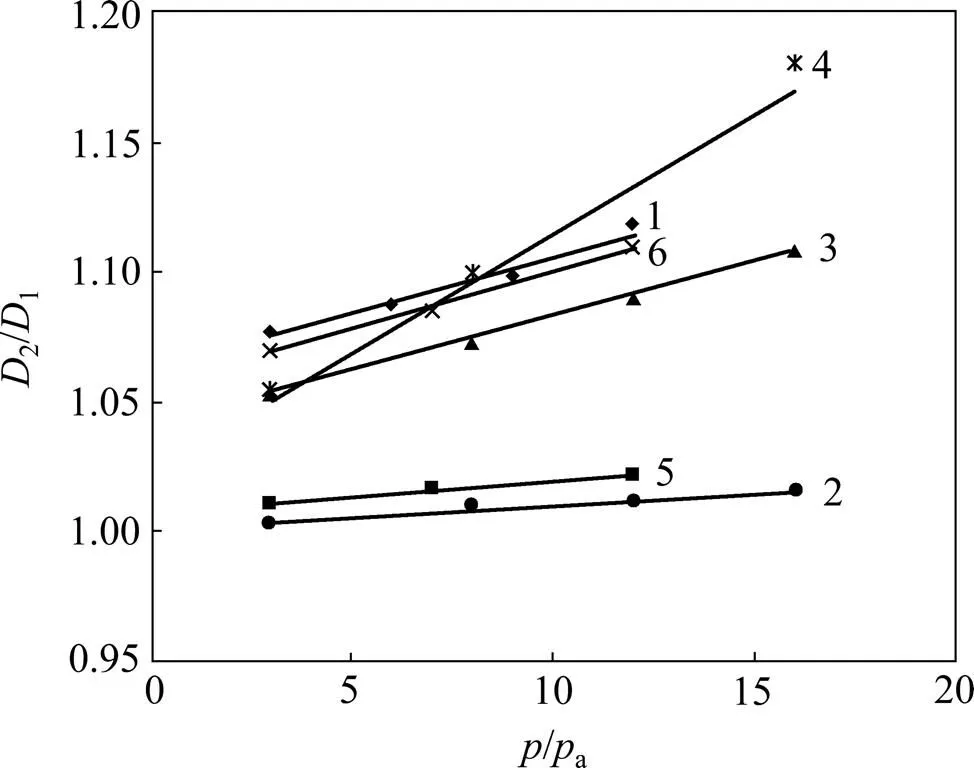
1—石英砂岩；2—片麻岩(级配1)；3—片麻岩(级配2)；4—砂板岩；5—砂砾岩；6—灰岩

由图7可以看出：2/1和/a关系曲线表现出显著的线性关系(2=0.943~0.996)。则2/1随/a的变化可表示为

式中：和为拟合参数。对图7中的6种材料，这2个拟合参数如表4所示。

2) 对图7中6种材料在不同围压时的相对破碎率r和破碎分形维数2进行整理，以r为横坐标，2/r为纵坐标绘制曲线，并用幂函数进行拟合，结果如图8所示。从图8可以看出：针对本文研究的不同母岩、不同级配和不同形状的6种粗粒土，破碎后的分形维数与颗粒相对破碎率之间有较好的对应关系，2/r与r的变化可以用式(6)来表示，即

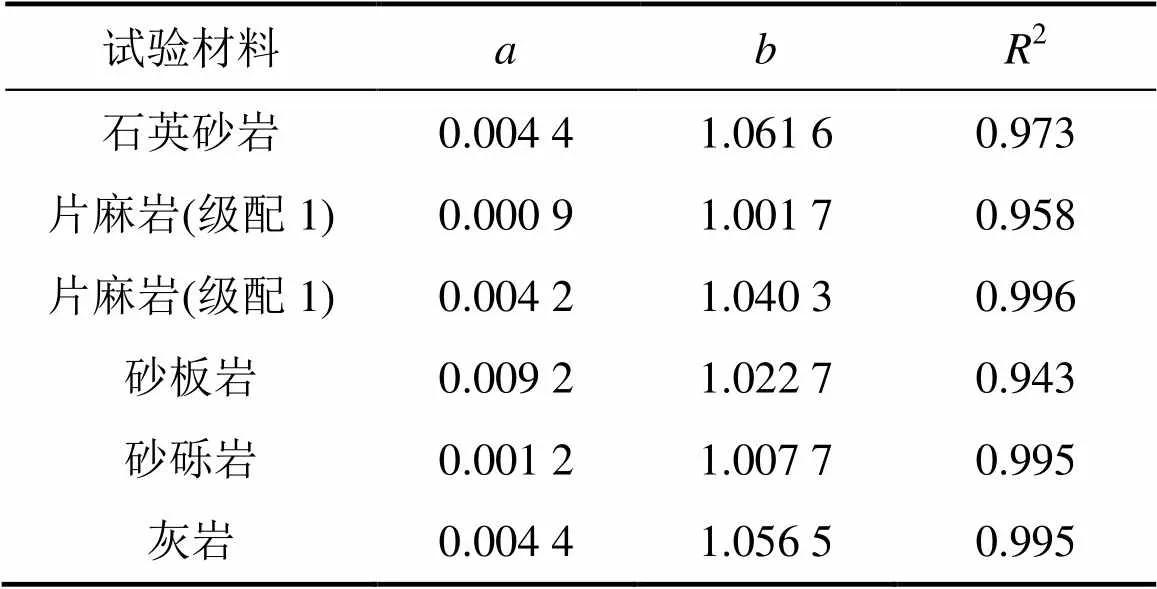
表4 各粗粒土的a和b拟合值

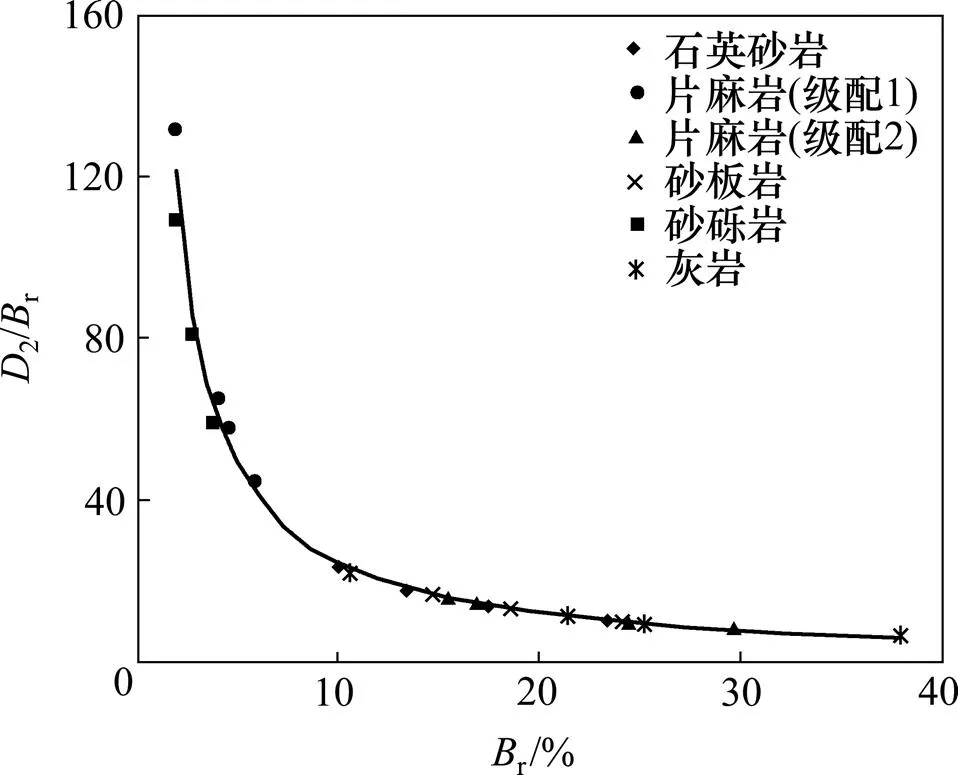
图8 D2/B­r−Br的线性拟合曲线

联合式(5)和式(6)得破碎前的分形维数与相对破碎率的关系式如式(7)所示：

因此，在破碎前分形维数和拟合参数和已知的情况下，可由式(7)来估算不同围压下粗粒土的相对破碎率。另外，由图7可以看出，破碎分形维数与相对破碎率的关系受母岩、级配和形状的影响，都是围绕在图7所示的幂函数曲线上。这也进一步说明级配连续土体的颗粒级配可以用分形维数表示。

4 结论

1) 所采用的分形模型能较好地适用于粗粒土，能采用分形维数来描述级配。

2) 各缩尺方法得到的粒度分形曲线形态有较大差别，与原始级配的粒度分形曲线有不同程度的偏离，缩尺粒径越小偏离程度越大，且缩尺级配的分形维数小于原型级配的分形维数。

3) 建立缩尺粒径和分形维数的内在联系，研究缩尺级配与原始级配分形维数的差异。

4) 基于分形理论的修正Hardin破碎指标r，从不同母岩材料、不同级配和不同颗粒形状的角度考虑粗粒土受力后的颗粒破碎程度。研究指出围压越大，破碎分形维数和相对破碎率越大，试验前粗粒土的分形维数越大，试验后相对破碎率越小。

5) 破碎后的分形维数与相对破碎率受母岩、级配和形状的影响呈幂函数的关系，通过破碎前的分形维数和拟合参数可估计不同围压下粗粒土的相对破 碎率。

[1] Indraratna B, Lackenby J, Christie D. Effect of confining pressure on the degradation of ballast under cyclic loading[J]. Geotechnique, 2005, 55(4): 325−328.

[2] 杨光, 张丙印, 于玉贞, 等. 不同应力路径下粗粒料的颗粒破碎试验研究[J]. 水利学报, 2010, 41(3): 338−342.

YANG Guang, ZHANG Bingyin, YU Yuzhen, et al. An experimental study on particle breakage of coarse-grained materials under various stress paths[J]. Journal of Hydraulic Engineering,2010, 41(3): 338−342.

[3] 刘汉龙, 秦红玉, 高玉峰, 等. 堆石粗颗粒料颗粒破碎试验研究[J]. 岩土力学, 2005, 26(4): 562−566. LIU Hanlong, QIN Hongyu, GAO Yufeng, et al. Experimental study on particle breakage of rockfill and coarse aggregates[J]. Rock and Soil Mechanics, 2005, 26(4): 562−566.

[4] 朱俊高, 王元龙, 贾华, 等.粗粒土回弹特性试验研究[J]. 岩土工程学报, 2011, 33(6): 950−954. ZHU Jungao, WANG Yuanlong, JIA Hua, et al. Experimental study on resilience behavior of coarse grained soils[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(6): 950−954.

[5] 孙海忠, 黄茂松. 考虑颗粒破碎的粗粒土临界状态弹塑性本构模型[J]. 岩土工程学报, 2010, 32(8): 1284−1290. SUN Haizhong, HUANG Maosong. Critical state elasto-plastic model for coarse granular aggregates incorporating particle breakage[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(8): 1284−1290.

[6] 贾宇峰，迟世春，林皋. 考虑颗粒破碎的粗颗粒土剪胀性统一本构模型[J]. 岩土力学, 2010, 31(5): 1381−1388.

JIA Yufeng, CHI Shichun, LIN Gao. Dilatancy unified constitutive model for coarse granular aggregates incorporating particle breakage[J]. Rock and Soil Mechanics, 2010, 31(5): 1381−1388.

[7] 陈生水，傅中志，韩华强，等. 一个考虑颗粒破碎的堆石料弹塑性本构模型[J]. 岩土力学, 2011, 33(10): 1489−1495.

CHEN Shengshui, FU Zhongzhi, HAN Huaqiang, et al. An elastoplastic model for rockfill materials considering particle breakage[J]. Rock and Soil Mechanics, 2011, 33(10): 1489−1495.

[8] 刘玉松, 方磊, 陈浩东. 论我国特殊土粒度分布的分形结构[J]. 岩土工程学报, 1993, 15(1): 23−30. LIU Yusong, FANG Lei, CHEN Haodong. Fractal structure of granularity distribution of regional soils in China[J]. Chinese Journal of Geotechnical Engineering, 1993, 15(1): 23−30.

[9] 徐永福, 刘斯宏, 董平. 粒状土体的结构模型[J]. 岩土力学, 2001, 22(4): 367−372.XU Yongfu, LIU Sihong, DONG Ping. Microstructural model for granular soil[J]. Rock and Soil Mechanics, 2001, 22(4): 366−372.

[10] 石修松, 程展林. 堆石料颗粒破碎的分形特性[J]. 岩石力学与工程学报, 2010, 29(增2): 3852−3857. SHI Xiusong, CHENG Zhanlin. Fractal behavior in crushing of rockfill material[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(Suppl 2): 3852−3857.

[11] 张肖宁, 孙杨勇. 粗集料的表面微观纹理的激光测量方法及分形性质研究[J]. 公路交通科技, 2011, 28(1): 19−24. ZHANG Xiaoning, SUN Yangyong. Research on measurement of surface micro-texture of aggregate using laser and its fractal character[J]. Journal of Highway and Transportation Research and Development, 2011, 28(1): 19−24.

[12] 徐永福, 史春乐. 用土的分形结构确定土的水份特征曲线[J]. 岩土力学, 1997, 18(2): 40−43. XU Yongfu, SHI Chunle. Calculation of soil-water characteristic curves by using fractal structure of soil[J]. Rock and Soil Mechanics, 1997, 18(2): 40−43.

[13] YU Boming, LI Jianhua. Some fractal characters of porous media[J]. Fractals, 2001, 9(3): 365−372.

[14] Tyler S W, Wheatcraft S W. Fractal scaling of soil particle size distributions: Analysis and limitations[J]. Soil Science Society of America Journal, 1992, 56(2): 362−369.

[15] 舒志乐. 土石混合体微结构分析及物理力学特性研究[D]. 成都: 西华大学建筑与土木工程学院, 2007: 21−29. SHU Zhile. Study on microstructure and mechanical characteristics of the earth-rock aggregate[D]. Chengdu: Xihua University. School of Architecture and Civil Engineering, 2007: 21−29.

[16] 傅华, 凌华, 蔡正银. 粗颗粒土颗粒破碎影响因素试验研究[J]. 河海大学学报, 2009, 37(1): 75−79. FU Hua, LING Hua, CAI Zhengyin. Influencing factors for particle breakage of coarse grained soil[J]. Journal of Hohai University, 2009, 37(1): 75−79.

[17] Einav I. Breakage mechanics—Part Ⅰ: Theory[J]. Journal of the Mechanics and Physics of Solids, 2007, 55: 1274−1297.

(编辑 刘锦伟)

Gradation of coarse grained soil and fractal geometry character of particle breakage

CHEN Liufen1, 2, GAO Zhuangping1, ZHU Jungao1, 2, YIN Jianhua3

(1. Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering, Hohai University, Nanjing 210098, China;2. Geotechnical Research Institution, Hohai University, Nanjing 210098, China;3. Department of Civil and Structure Engineering, Hongkong Polytechnic University, Hongkong 999077, China)

The applicability of soil cumulative mass particle-size distribution for coarse grained soil was verified, and the change rule of fractal dimension was analyzed in the situation of different particle sizes and scale methods. The connection between scale gradation and original gradation was also established through fractal dimension. Relative breakage rate was calculated according to the triaxial tests with different parent rocks, gradations and particle shapes. The correlation between fractal dimension and relative breakage rate was also discussed. The results show that fractal dimension can quantitatively describe original gradation and scale gradations. There exist great differences between fractal dimension curves of particle size with different scale methods, and all of them deviate from original gradation’s, the smaller scale size is, the bigger the deviation is. In the four scale methods, an excellent linear relationship between fractal dimension and the logarithm values of particle size has been found. The bigger the pressure is, the larger the broken fractal dimension and relative breakage rate is. The relative breakage rate decreases with the increase of fractal dimension before test. The broken fractal dimension and relative breakage rate displays a power functional relation under the condition of different parent rocks, gradations and particle shapes. Therefore, relative breakage rate of different pressure can be estimated through fractal dimension and fitting parameters.

coarse grained soil; gradation; particle breakage; fractal dimension; relative breakage rate

10.11817/j.issn.1672-7207.2015.09.038

TU411

A

1672−7207(2015)09−3446−08

2014−09−17；

2014−11−03

国家重点基础研究发展规划(973计划)项目(2013CB036404)；高等学校博士学科点专项科研基金资助项目(20110094110002)；高等学校学科创新引智计划项目(B13024) (Project(2013CB036404) supported by the National Basic Research Program (973 Program) of China; Project(20110094110002) supported the Specialized Research Fund for the Doctoral Program of High Education; Project(B13024) supported by the Program of Introducing Talents of Discipline for Universities)

朱俊高，教授，从事土体本构关系研究；E-mail: zhujungao@hhv.edu.cn