岩锚梁稳定性影响因素模糊灰色关联分析模型及其应用

陈强，周先雁



岩锚梁稳定性影响因素模糊灰色关联分析模型及其应用

陈强1, 2，周先雁1

(1. 中南林业科技大学土木工程与力学学院，湖南长沙，410004;2. 湖南城市学院土木工程学院，湖南益阳，413000)

针对岩锚梁稳定性具有的不确定性、模糊性与灰色性，采用模糊理论与灰色关联理论相结合的方法建立模糊灰色关联分析模型，并对岩锚梁稳定性影响因素进行模糊灰色关联分析，得出各影响因素对岩锚梁稳定性的影响程度及各影响因素间的关联程度。研究结果表明：各因素对岩锚梁的稳定性影响程度不一，围岩形变对其影响最大，其次是锚杆应力和围岩开合度，对岩锚梁稳定性影响最小的是围岩温度。研究结果可为岩锚梁混凝土浇筑施工及投入运行提供参考。

岩锚梁；稳定性；影响因素；模糊灰色关联分析

自20世纪80年代以来，作为一种新型的吊车梁结构的岩锚梁结构[1]在我国二滩、小浪底、百色水利工程、万家寨引黄工程、江垭、鲁布革、三峡、江垭、东风、小湾等大规模地下工程中成功应用。与其他的吊车梁结构相比，岩锚梁承受工作状态下桥机以及自重等受力，并通过受拉、受压长锚杆将受力传递给混凝土梁固定的两侧岩壁当中，因此，对混凝土梁固定的两侧岩壁的承载能力及稳定性进行分析显得十分重要。目前，国内外主要采用仿真分析或实验方法研究岩锚梁的施工工艺和运行状况，取得了较好的研究效果。例如，李新平等[2]在不同的岩石条件下采用现场实验对钻孔工艺及爆破参数进行了相应优化；王俤剀等[3]分析了地下厂房岩锚梁裂缝成因；傅少君等[4]采用有限元方法对岩锚梁的受力及破坏机制进行了研究。这些研究并没有对岩锚梁稳定性影响因素进行有效辨析。考虑到施工过程中岩锚梁稳定性影响因素主要包括围岩温度、围岩开合度(即开挖施工过程中出现的岩锚梁混凝土纵向裂缝长度)、梁体围岩变形和锚杆应力等[5]，考虑围岩温度、围岩开合度、梁体围岩变形和锚杆应力等影响因素之间的耦合作用机制存在着较大的不确定性、模糊性与灰色性，金丰年等[6]尽管对岩锚梁稳定性进行了灰色关联分析，但分析过程未体现岩锚梁稳定性影响因素的不确定性和模糊性。因此，如何有效地辨识岩锚梁围岩温度、围岩开合度、梁体围岩变形和锚杆应力等影响因素对岩锚梁稳定性的影响程度以及各影响因素之间的相关程度显得十分重要。将模糊理论[7−8]和灰色关联分析方法[9−13]相结合，则可客观地对岩锚梁稳定性影响因素进行关联分析，且对岩锚梁稳定性影响因素样本容量的要求较少，不要求数据具有典型的分布规律[14−15]。为此，本文作者将模糊理论与灰色系统理论相结合，提出新型的模糊灰色关联分析模型，并将其应用于岩锚梁稳定性影响因素的关联分析，以便为岩锚梁稳定性评价提供参考依据。

1 岩锚梁稳定性影响因素模糊灰色关联分析模型的建立

1.1 参考序列的确定

参考序列是1个或多个用于反映岩锚梁稳定性的数据序列，可由不同表征岩锚梁稳定性的统计数据组成，每组数据的变化规律可反映岩锚梁稳定性某一方面的发展趋势或变化情况。岩锚梁稳定性影响因素模糊灰色关联分析模型中的参考序列的表现形式如下：

式中：Y为岩锚梁稳定性影响因素模糊灰色关联分析模型中的第个参考序列；=1, 2, …,；[y(1),y(2), …,y()]为岩锚梁稳定性影响因素模糊灰色关联分析模型中的第个参考序列的具体表现形式，反映y变化规律。

1.2 比较序列的确定

比较数列是反映岩锚梁稳定性的影响因素的数据序列。假设被研究岩锚梁稳定性的影响因素有个，而这些因素影响的被研究工况有种，则记种工况下岩锚梁稳定性的影响因素的相应向量矩阵如下：

式中：为岩锚梁稳定性影响因素模糊灰色关联分析模型中参考序列Y所对应的比较序列。该岩锚梁稳定性影响因素模糊灰色关联分析模型中的比较序列有个影响因素的向量，其中第个为x(=1, 2, …,)，在这些因素的影响下有种工况，第种工况记为x() (=1, 2, …,)。

1.3 原始数据的无量纲化

在岩锚梁稳定性影响因素模糊灰色关联分析模型中，很多研究因素具有不同的物理意义和量纲，为减少因此而产生的识别及分析误差，各个具有不同量纲的特征参数在计算之前需进行无量纲化。无量纲化方法有很多，本文采用数据区间化方法对岩锚梁稳定性影响因素模糊灰色关联分析模型中参考序列和对比序列原始数据进行无量纲化转换，即对于参考序列原始数据，无量纲化转换形式可表示为

对于参考序列和对比序列原始数据，无量纲化转换形式可表示为

1.4 模糊隶属度余弦值的计算

考虑到夹角余弦法不受岩锚梁稳定性影响因素模糊灰色关联分析模型中数据的线性比例关系的影响，2个因素之间的相似度由2个参数的夹角余弦判断，故采用夹角余弦法建立岩锚梁稳定性影响因素模糊灰色关联分析模型中的模糊相似矩阵，其具体表现形式为

1.5 灰色关联度模型

岩锚梁稳定性影响因素模糊灰色关联分析模型中所有比较序列需要与参考序列进行差运算，则灰色关联度模型的计算公式如下：

式中：ξ() (=1, 2, …,;1, 2, …,)为岩锚梁稳定性影响因素模糊灰色关联分析模型中参考序列Y和比较序列X中2个对应点的关联系数；min为Y或X中所有对应元素的最小绝对差；max为Y或X中所有对应元素的最大绝对差；Δ()为参考序列中第个点与比较序列的第个点的绝对差；为灰色关联度模型的分辨系数。Y与X中所有对应元素的最小绝对差min的具体表现形式为

最大绝对差max体现了岩锚梁稳定性影响因素模糊灰色关联分析模型的整体特性，其具体表现形式为

岩锚梁稳定性影响因素模糊灰色关联分析模型中参考序列中第个点与比较序列第个点的绝对差Δ()的具体表现形式为

灰色关联度模型中分辨系数的本质为最大绝对差的权重，分辨系数的取值需要满足岩锚梁稳定性影响因素模糊灰色关联分析模型中关联度的整体性和抗干扰性，其过大或过小都不能正确反映研究对象间的关联性。

岩锚梁稳定性影响因素模糊灰色关联分析中，灰色关联度模型中的分辨系数可采用以下方法确定。

E≤≤1.5E(11)

当max≤3时，有

1.5E≤≤2.0E(12)

式中：max＞3，则表示岩锚梁稳定性影响因素模糊灰色关联分析模型中参考序列或对比序列中的数据出现异常值；max≤3，说明模型中参考序列或对比序列中的数据正常。

1.6 欧氏灰色关联度确定

为提高岩锚梁稳定性影响因素模糊灰色关联分析模型评定精度，采用欧氏距离表示岩锚梁稳定性影响因素模糊灰色关联分析模型中参考序列和比较序列的差异程度。为此，定义不同因子在岩锚梁稳定性影响因素模糊灰色关联分析模型中参考序列或对比序列中的权向量为

w=(1j,2j, …,w)；=1, 2, …,(13)

则岩锚梁稳定性影响因素模糊灰色关联分析模型中参考序列或对比序列中的欧式灰色关联度r/的计算公式为

1.7 改进模糊灰色关联度的确定

将利用夹角余弦值方法计算的模糊隶属系数以及灰色关联系数进行合并，可得到岩锚梁稳定性影响因素模糊灰色关联分析模型的模糊灰色关联度R为

2 工程实例应用

以某地下大型洞库岩锚梁稳定性影响因素实测数据为例，运用本文所建立的岩锚梁稳定性影响因素的改进模糊灰色关联分析模型解决具体的工程实际问题。

某地下大型洞库所处地质条件复杂，工程洞室具有跨度大和纵向深的特征。考虑到工程洞室中所建岩锚梁位置存在部分Ⅲ类以及Ⅳ类围岩，因此，在岩锚梁施工中对其该区段加强监测，评估岩锚梁施工过程的安全性。为此，本文选取如表1所示的该区段某监测断面的围岩开合度、围岩温度、围岩变形以及锚杆应力等监测参数，采用改进模型进行分析研究。

2.1 当参考序列为围岩开合度时

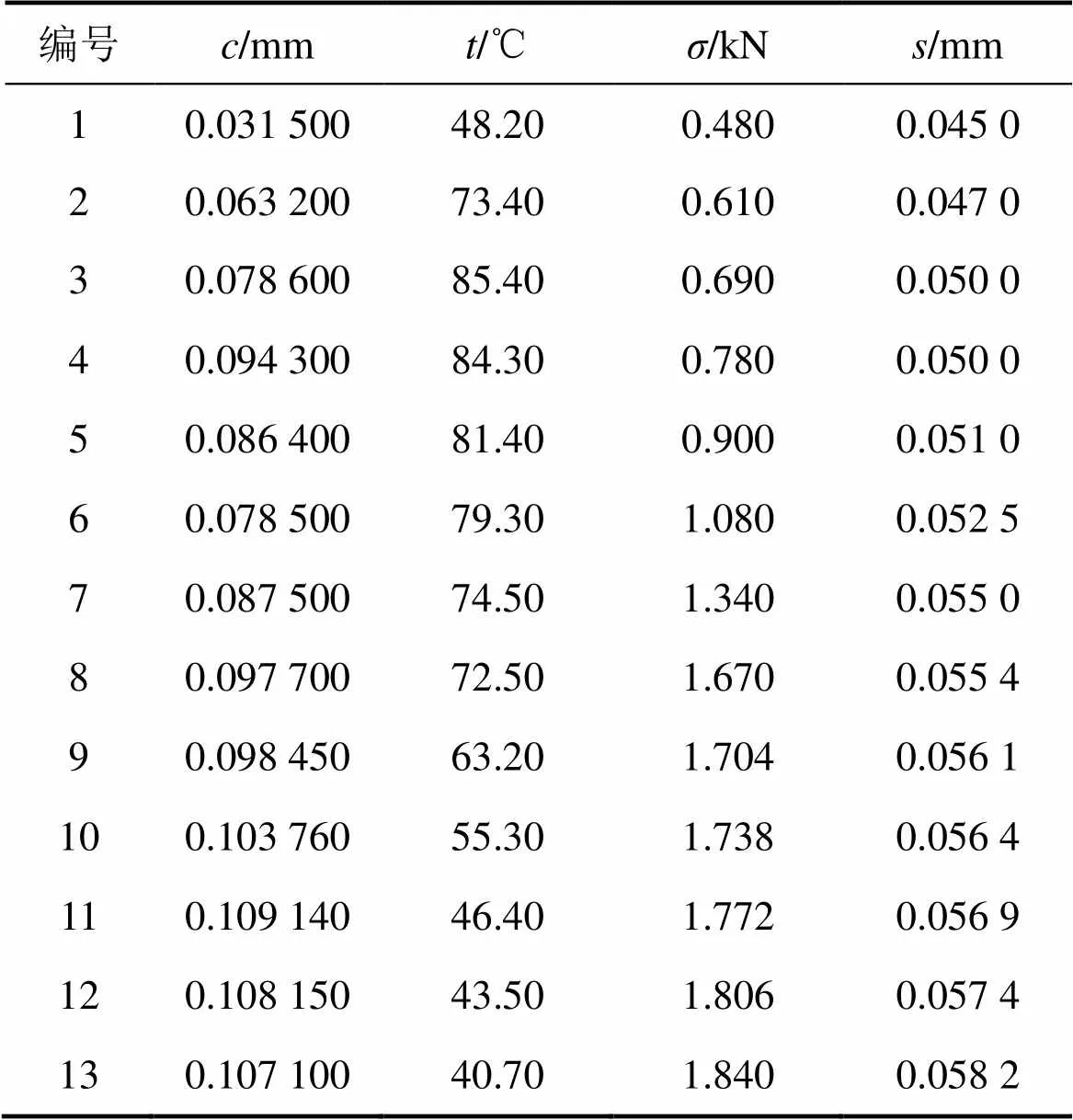
表1 岩锚梁施工过程监测断面监测结果

当参考序列为围岩开合度时，围岩温度、锚杆应力以及围岩变形所组成的矩阵为比较序列，则

通过式(4)无量纲化后得到以下系数矩阵：

将该系数矩阵代入式(7)和式(8)得min=0，max=1，则由式(9)得到参考序列与比较序列的绝对差矩阵：

将以上所得结果代入式(6)可得各影响因素的灰色关联系数矩阵：

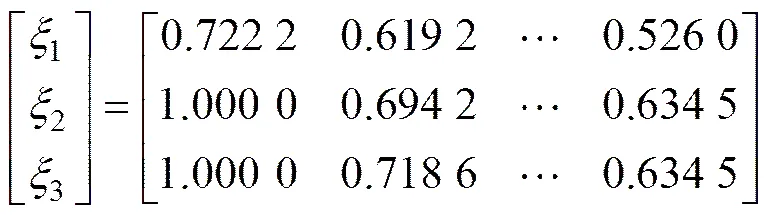
认为各数据编号对各影响因素的影响权重是均衡的，不存在本质上的区别，所以，本文取w=(1j,2j,…,w)=1/26(其中=26；=1, 2, 3)。将所得的灰色关联系数矩阵代入式(14)可得围岩温度、锚杆应力以及围岩变形对围岩开合度的加权灰色关联度1′，据式(5)和(15)可得围岩温度、锚杆应力以及围岩变形对围岩开合度的模糊隶属度夹角余弦1以及模糊灰色关联度1，如表2所示。

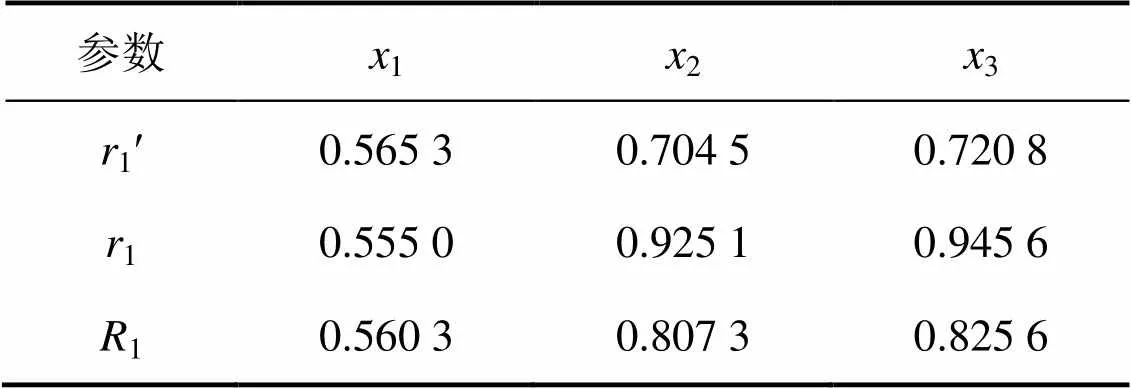
表2 影响因素对围岩开合度的模糊灰色关联分析结果

表2表明：围岩温度、锚杆应力以及围岩变形对围岩开合度的模糊灰色关联度1= [11,12,13]=[0.560 3, 0.807 3, 0.825 6]，显然有13＞12＞11。因此，围岩变形和围岩开合度之间的模糊灰色关联度较大，说明围岩开合度受围岩变形的影响较大，应采取相应的应对措施尽量减小围岩变形。

2.2 当参考序列为围岩温度时

当参考序列为围岩温度时，围岩开合度、锚杆应力以及围岩变形所组成的矩阵为比较序列，则有

通过式(4)无量纲化后得到以下系数矩阵：

将该系数矩阵代入式(7)和(8)得min=0，max=1，则由式(9)得到参考序列与比较序列的绝对差矩阵：

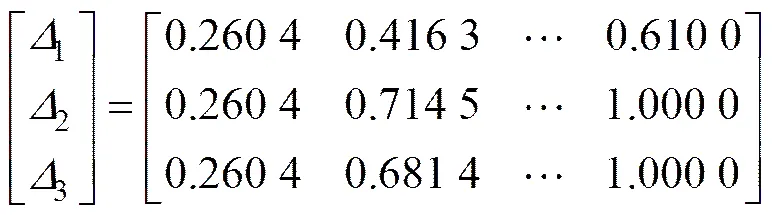
将以上所得结果代入式(6)可得各影响因素的灰色关联系数矩阵：

认为各数据编号对各影响因素的影响权重是均衡的，不存在本质上的区别，所以，本文取w=(1j,2j,…,w)=1/26(其中=26；=1, 2, 3)。将所得的灰色关联系数矩阵代入式(14)可得围岩开合度、锚杆应力以及围岩变形对围岩温度的加权灰色关联度2′，根据式(5)和(15)可以得围岩开合度、锚杆应力以及围岩变形对围岩温度的模糊隶属度夹角余弦2以及模糊灰色关联度2，如表3所示。

表3表明：围岩开合度、锚杆应力以及围岩变形对围岩温度的模糊灰色关联度2= [21,22,23]=[0.604 6, 0.470 6, 0.514 9]，显然有21＞23＞22。因此，围岩开合度和围岩温度之间的模糊灰色关联度较大，说明围岩温度受围岩开合度的影响相对较大，应采取相应的应对措施尽量减小围岩开合度。

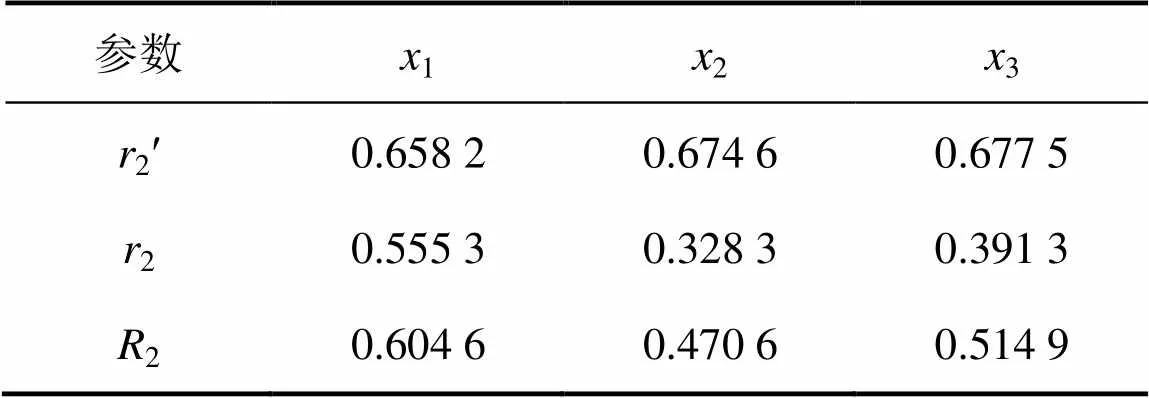
表3 影响因素对围岩温度的模糊灰色关联分析结果

2.3 参考序列为锚杆应力时

当参考序列为锚杆应力时，围岩开合度、围岩温度以及围岩变形所组成的矩阵为比较序列，则

通过式(4)无量纲化后得到以下系数矩阵：

将该系数矩阵代入式(7)和(8)得min=0，max=1，则由式(9)得到参考序列与比较序列的绝对差矩阵：

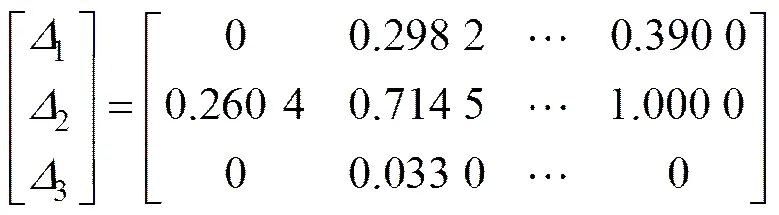
将以上所得结果代入式(6)可得各影响因素的灰色关联系数矩阵：

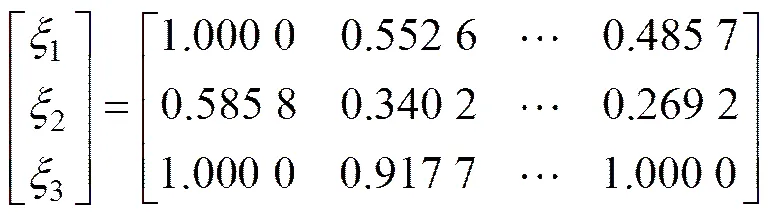
认为各数据编号对各影响因素的影响权重是均衡的，不存在本质上的区别，所以，本文取w=(1j,2j,…,w)=1/26(其中=26；=1, 2, 3)。将所得的灰色关联系数矩阵代入式(14)可得围岩开合度、围岩温度以及围岩变形对锚杆应力的加权灰色关联度3′，根据式(5)和式(15)可得围岩开合度、围岩温度以及围岩变形对锚杆应力的模糊隶属度夹角余弦3和模糊灰色关联度3，如表4所示。

表4 影响因素对锚杆应力的模糊灰色关联分析结果

表4表明，围岩开合度、围岩温度以及围岩变形对锚杆应力的模糊灰色关联度3=[31,32,33]=[0.728 9, 0.381 1, 0.949 4]，显然有33＞31＞32。因此，围岩变形和锚杆应力之间的模糊灰色关联度值较大，说明锚杆应力受围岩变形的影响较大，应采取相应的应对措施尽量减小围岩变形。

2.4 参考序列为形变时

当参考序列为形变时，围岩开合度、围岩温度以及锚杆应力所组成的矩阵为比较序列，则

通过式(4)无量纲化后得到以下系数矩阵：

将该系数矩阵代入式(7)和(8)得min=0，max=1，则由式(9)得到参考序列与比较序列的绝对差矩阵：

将以上所得结果代入式(6)可得各影响因素的灰色关联系数矩阵：

认为各数据编号对各影响因素的影响权重是均衡的，不存在本质上的区别，所以，本文取w=(1j,2j,…,w)=1/26(其中=26；=1, 2, 3)。将所得的灰色关联系数矩阵代入式(14)可得围岩开合度、围岩温度以及锚杆应力对围岩变形的加权灰色关联度4′，根据式(5)和式(15)可得围岩开合度、围岩温度以及锚杆应力对围岩变形的模糊隶属度夹角余弦4和模糊灰色关联度4，如表5所示。

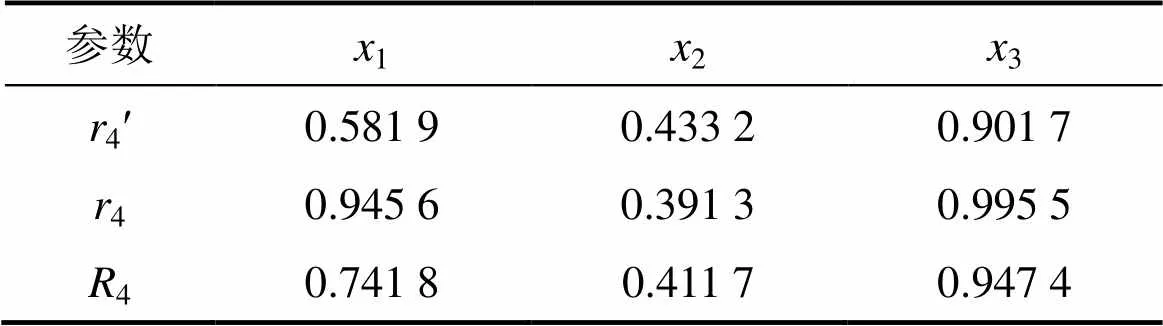
表5 影响因素对围岩形变的模糊灰色关联分析结果

表5表明：围岩开合度、围岩温度以及锚杆应力对围岩变形的模糊灰色关联度为4=[41,42,43]=[0.741 8, 0.411 7, 0.947 4]，显然有43＞41＞42。因此，锚杆应力和围岩变形之间的模糊灰色关联度值较大，说明围岩变形受锚杆应力的影响较大，应采取相应的应对措施尽量减小锚杆应力。

2.5 计算结果讨论

图1所示为以上4种不同参考序列下所得到的岩锚梁稳定性影响因素模糊灰色关联度11，12，13，21，22，23，31，32，33，41，42和43的对比结果。图1表明4种不同参考序列下所得到的岩锚梁稳定性影响因素模糊灰色关联度满足：33＞43＞13＞12＞41＞31＞0.7＞21＞11＞0.5＞23＞22＞42＞32。

可见不同参考序列下所得到的岩锚梁稳定性影响因素模糊灰色关联度可分为较明显的3类：1) 模糊灰色关联度大于0.700 0。主要包括锚杆应力对围岩开合度的模糊灰色关联度12、围岩变形对围岩开合度的模糊灰色关联度13、围岩开合度对锚杆应力的模糊灰色关联度31、围岩变形对锚杆应力的模糊灰色关联度33、围岩开合度对围岩变形的模糊灰色关联度41以及锚杆应力对围岩变形的模糊灰色关联度43共6个；2)模糊灰色关联度介于0.500 0~0.700 0之间，主要包括围岩温度对围岩开合度的模糊灰色关联度11、围岩开合度对围岩温度的模糊灰色关联度21、围岩变形对围岩温度的模糊灰色关联度23等；3)模糊灰色关联度小于0.500 0，主要包括锚杆应力对围岩温度的模糊灰色关联度22、围岩温度对锚杆应力的模糊灰色关联度32和围岩变形对围岩开合度的模糊灰色关联度42共3个。

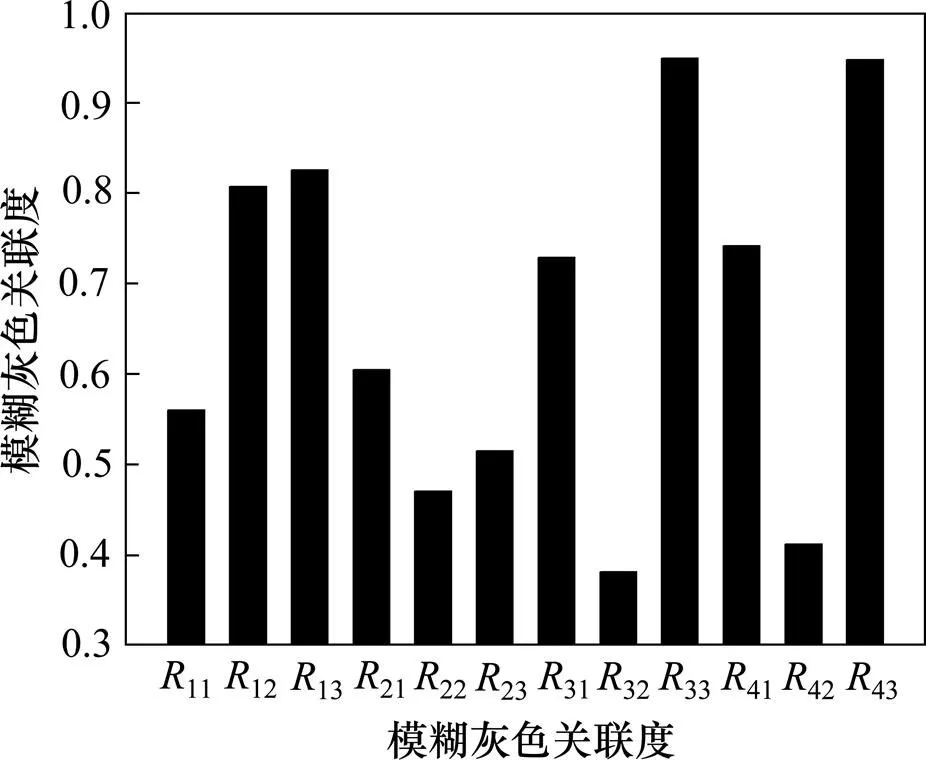
图1 岩锚梁稳定性影响因素模糊灰色关联度对比

这也解释了岩锚梁浇筑施工时，随着梁体内部混凝土锚杆应力以及围岩开合度的变化的原因。梁体的围岩变形随之开展，其早期的围岩变形大多是锚杆应力升高和围岩开合度变大所导致的，因此，必须严格控制混凝土的锚杆应力以及围岩开合度变化，跟踪监测，作好混凝土的早期养护工作。

表6所示为以上参数互为影响因素时，岩锚梁稳定性影响因素模糊灰色关联分析结果。令表示互为影响因素时，岩锚梁稳定性影响因素模糊灰色关联度求和，则可定义=21+31+41，=11+32+42，=12+22+43，=13+23+33，可知＞＞＞。

表6表明：围岩形变在岩锚梁的稳定中起到主导作用，是4个因素中的最主要影响因素，其次为锚杆应力和围岩开合度，围岩温度在岩锚梁的稳定中起到相对较小的影响。这与某地下大型洞库岩锚梁施工现场监测实际结果较接近。随着围岩变形的开展，梁体与接触处围岩之间的缝隙也随之发展，两者是相关的。围岩变形和锚杆应力之间的模糊灰色关联度达到0.949 4，是计算值中最大的，说明围岩变形对锚杆应力的影响较大，应采取相应的应对措施。

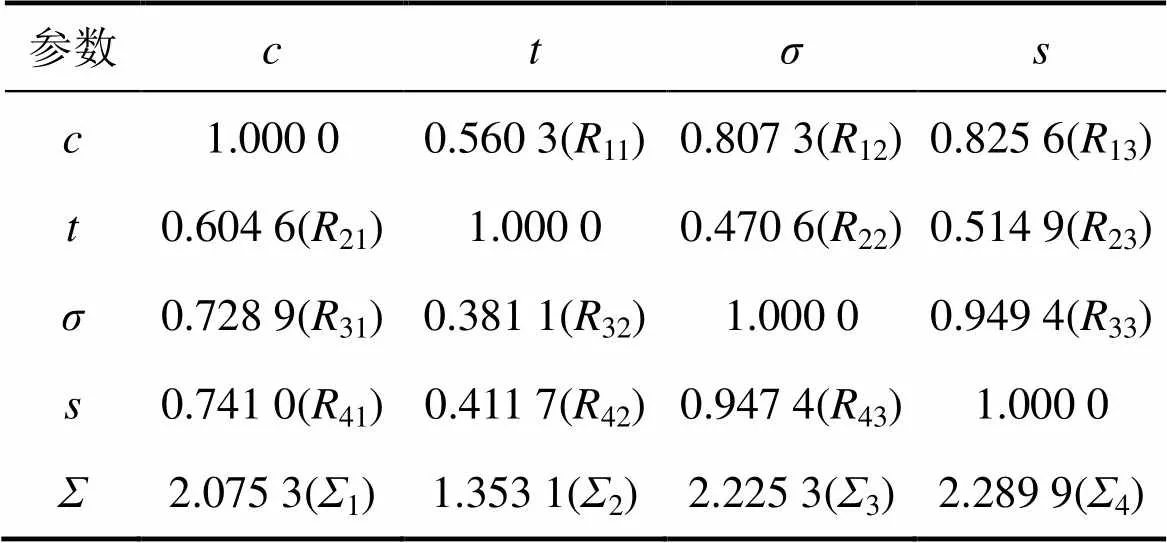
表6 互为影响因素时岩锚梁的稳定性影响因素模糊灰色关联分析结果

显然，模糊灰色关联分析模型可克服岩锚梁稳定性分析中诸如样本量小并且规律性不明显的不足，可为辨析影响锚梁稳定性的主要因素提供快速有效方法，且其研究结果也可为岩锚梁施工中采取有效措施控制其稳定性提供较好参考依据。

3 结论

1) 采用模糊理论和灰色关联理论相结合方法建立了模糊灰色关联分析模型，并对岩锚梁稳定性影响因素进行了模糊灰色关联分析，得出了各影响因素对岩锚梁稳定性的影响程度及各影响因素间的关联 程度。

2) 围岩形变对岩锚梁稳定性影响最大的因素，其次是锚杆应力和围岩开合度，对岩锚梁稳定性影响最小的是围岩温度。

3) 本文建立的模糊灰色关联分析模型有利于样本量小且具有不确定性、模糊性与灰色性的复杂系统影响因素的模糊灰色关联分析。

[1] 涂志军, 崔巍. 小湾水电站地下厂房岩锚梁现场试验研究[J]. 岩土力学, 2007, 28(6): 1139−1144. TU Zhijun, CUI Wei. Study on in-situ test of rock-bolted crane girder in Xiaowan Hydropower Station[J]. Rock and Soil Mechanics, 2007, 28(6): 1139−1144.

[2] 李新平, 徐剑, 张成良, 等. 溪洛渡电站地下厂房岩台开挖爆破试验研究[J]. 爆破, 2008, 25(2): 30−33. LI Xinping, XU Jian, ZHANG Chengliang, et al. Experimental study on rock bench blasting excavation in underground workshop of Xiluodu Hydropower Station[J]. Blasting, 2008, 25(2): 30−33.

[3] 王俤剀, 彭琦, 汤荣, 等. 地下厂房岩锚梁裂缝成因分析[J]. 岩石力学与工程学报, 2007, 26(10): 2125−2129. WANG Dikai, PENG Qi, TANG Rong, et al. Causes analysis of cracking of rock-bolted crane girder in an underground powerhouse[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(10): 2125−2129.

[4] 傅少君, 邱焕峰, 于英姬, 等. 岩壁吊车梁有限元分析的关键技术问题研究[J]. 岩石力学与工程学报, 2008, 27(10): 2124−2129. FU Shaojun, QIU Huanfeng, YU Yingji, et al. Study on key problems of finite element analysis of crane beam on rock wall[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(10): 2124−2129.

[5] 贺如平, 张强勇, 王建洪, 等. 大岗山水电站坝区辉绿岩脉压缩蠕变试验研究[J]. 岩石力学与工程学报, 2007, 26(12): 2495−2502. HE Ruping, ZHANG Qiangyong, WANG Jianhong, et al. Study on compressive creep test on diabasic dike at dam site of Dagangshan hydropower station[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(12): 2495−2502.

[6] 金丰年, 欧阳科峰, 周雪峰, 等. 岩锚梁稳定性的关联分析[J]. 解放军理工大学学报(自然科学版), 2005, 6(2): 146−148. JIN Fengnian, OUYANG Kefeng, ZHOU Xuefeng, et al. Grey relation analysis in stability for rock-bolt crane girder[J]. Journal of PLA University of Science and Technology, 2005, 6(2): 146−148.

[7] ZUO Hongyan. Empirical study on multilevel fuzzy entropy weight performance evaluation model of the petroleum products export processing enterprises in China[J]. Applied Mathematics & Information Sciences, 2015, 9(4): 2185−2193.

[8] WANG Shuangying, ZUO Hongyan. Safety diagnosis on coal mine production system based on fuzzy logic inference[J]. Journal of Central South University, 2012, 19(2): 477−481.

[9] E Jiaqiang, LI Yuqiang, GONG Jinke. Function chain neural network prediction on heat transfer performance of oscillating heat pipe based on grey relational analysis[J]. Journal of Central South University, 2011, 18(5): 1733−1738.

[10] Deli I, Çağman N. Intuitionistic fuzzy parameterized soft set theory and its decision making[J]. Applied Soft Computing, 2015, 28: 109−113.

[11] Wang Z J, Wang Q, Ai T. Comparative study on effects of binders and curing ages on properties of cement emulsified asphalt mixture using gray correlation entropy analysis[J]. Construction and Building Materials, 2014, 54(2): 615−622.

[12] Mao D F, Duan M L, Li X Z, et al. Selection of deepwater floating oil platform based on grey correlation[J]. Petroleum Exploration and Development, 2013, 40(6): 796−800.

[13] 鄂加强, 龙艳平, 王曙辉, 等. 动力锂离子电池充电过程热模拟及影响因素灰色关联分析[J]. 中南大学学报(自然科学版), 2013, 44(3): 998−1005. E Jiaqiang, LONG Yanping, WANG Shuhui, et al. Thermal simulation on dynamic lithium-ion battery during charge and its grey relational analysis[J]. Journal of Central South University (Science and Technology), 2013, 44(3): 998−1005.

[14] Zhang X, Jin F, Liu P D. A grey relational projection method for multi-attribute decision making based on intuitionistic trapezoidal fuzzy number[J]. Applied Mathematical Modelling, 2013, 37(5): 3467−3477.

[15] Wei G W. Gray relational analysis method for intuitionistic fuzzy multiple attribute decision making[J]. Expert Systems with Applications, 2011, 38(9): 11671−11677.

(编辑 陈灿华)

Fuzzy grey relation analysis model on influence factors for stability of rock-bolt crane girder and its application

CHEN Qiang1, 2, ZHOU Xianyan1

(1. School of Civil Engineering and Mechanics, Central South University of Forestry and Technology, Changsha 410004, China;2. School of Civil Engineering, Hunan City College, Yiyang 413000, China)

Considering the uncertainty, fuzziness and grayness of the stability of the rock-bolt crane girder, fuzzy theory and grey relational theory were used to establish an advanced fuzzy grey relational analysis model, the influence factors for the stability of the rock-bolt crane girder were analyzed by using the advanced fuzzy grey relational analysis model, and the relational degree of the influence factors on stability of the rock-bolt crane girder and the correlativity among the influence factors were gotten. The results show that varying degrees of influence of various factors on the stability of the rock-bolt crane girder are obvious, the maximum influence factor on the stability of the rock-bolt crane girderis the deformation of the surrounding rock, the next are the stress of the anchor and the opening degree of the surrounding rock, and the minimum influence factor on the stability of rock-bolt crane girderis the temperature of the surrounding rock. The research results can provide reference for construction of the rock-bolt crane girder.

rock-bolt crane girder; stability; influence factor; fuzzy grey relational analysis

10.11817/j.issn.1672-7207.2015.09.044

TU926

A

1672−7207(2015)09−3488−08

2015−02−01；

2015−04−22

湖南省科技计划项目(2012GK3066) (Project(2012GK3066) supported by Science and Technology Plan Program of Hunan Province)

陈强，博士研究生，副教授，从事土木工程研究；E-mail: 846039016@qq.com