基于小样本试验的大型回转支承剩余寿命预测
封杨,黄筱调,陈捷,王华,洪荣晶
基于小样本试验的大型回转支承剩余寿命预测
封杨,黄筱调,陈捷,王华,洪荣晶
(南京工业大学机械与动力工程学院,江苏南京,210009)
提出一种基于小样本的大型回转支承剩余寿命预测方法,首先基于改进的威布尔分布理论建立回转支承剩余寿命预测的可靠性模型,然后基于赫兹理论分析回转支承滚道载荷分布规律,并结合Archard磨损理论和逆幂率加速寿命模型提出通过小样本试验估计预测模型参数的方法,最后用QNA−730−22内齿式回转支承进行验证。研究结果表明:该方法能够通过一次全寿命试验建立起多个疲劳载荷下多个滚道样本准确的寿命模型,相对于NREL设计指南和ISO281的疲劳寿命计算方法,该方法更接近真实试验数据,并且相对传统可靠性建模方法能节省大量的时间和费用,为企业制定及时的主动维护策略提供参考。
威布尔分布;回转支承;寿命预测;小样本试验
大型回转支承作为风机、工程机械上的大型回转连接件,通常会承受极大的轴向力、径向力和倾覆力矩。剩余寿命的准确预测能够帮助操作人员及时维护或更换回转支承,从而避免事故和减少不必要的维护。因此,对回转支承进行的剩余寿命的准确预测很有必要。Kim等[1]用SVM将信号分类,用健康状态估计法建立泵用轴承的衰退模型。Benkedjouh等[2]用ISOMAP提取振动信号特征,再用SVR进行轴承的寿命预测。Medjaher等[3]用高斯混合HMM将历史数据建立起衰退模型,将在线监测的信号用于轴承剩余寿命预测。然而,以上方法均针对中小型轴承,大型回转支承由于其极低的转速,低振动信号的信噪比,常用的特征提取方法不适用[4]。除此之外,Potočnik等[5−7]基于应变−寿命理论,用有限元计算出回转支承滚道次表面剪应力,报道不同类型回转支承疲劳寿命计算过程。Gao等[8]将ISO281疲劳寿命计算中的可靠度系数1用Lundberg−Palmgren理论中的可靠度代替,建立回转支承疲劳寿命与几何参数、材料特性、承受载荷之间的关系。但是,回转支承直径通常为0.8~5.0 m,其滚珠滚道的载荷分布为非线性,若利用有限元方法计算[5−7],将花费大量的时间且结果并非完全可靠。同时,传统的威布尔分布的建模过程[8]需大量的历史失效数据,这需要批量对回转支承进行疲劳寿命试验。而无论是利用自制的试验台,还是利用现场安装回转支承的设备,批量的回转支承疲劳寿命试验从时间和经济成本方面都不可接受。为解决上述问题,本文作者针对大型回转支承提出一个基于小样本试验的剩余寿命预测方法,可根据实际工况,对任意载荷的回转支承进行剩余寿命预测:首先,根据威布尔分布推导出剩余寿命预测模型;然后,结合Archard磨损理论[9]和逆幂率加速寿命模型[10]提出小样本加速寿命试验方法进行预测模型的参数估计;最后用某公司的QNA−730−22回转支承进行验证。本文所提方法相比NREL[11]和ISO281[12]中的疲劳寿命计算方法更接近工程实际,能有效减少不必要的维护和更换,为企业节省更多资源。
1 剩余寿命预测模型
威布尔分布由Weibull[13]在1951年研究滚珠轴承的疲劳寿命时提出。几十年来,很多学者对威布尔分布在轴承寿命中的应用进行研究,大量试验证明,滚动轴承的寿命分布近似服从二参数威布尔分布[14],威布尔分布的失效函数()为
可靠度函数()为
回转支承滚道的破坏主要由交变应力循环引起滚道的疲劳裂纹、剥落等,随回转支承转过圈数的增加,应力循环次数成比例增长,因此,其疲劳寿命通常用回转支承转过的圈数来表示。若一个回转支承转过圈,仍能正常运行,则称其年龄为。一个年龄为的回转支承运行至失效所经历的圈数称为剩余疲劳寿命,记为T。T是随机变量,对于任意实数,事件{T}的概率为

由式(1)和式(2)可得
因此
将式(5)代入式(3)得
因此,年龄为的回转支承的剩余寿命分布函数F()为
由此可得可靠度R()下年龄为的回转支承的剩余寿命为
2 剩余寿命预测模型的参数估计
与普通中小轴承不同的是,回转支承通常在内圈或外圈上加工出齿轮用以驱动,加工出齿轮的圈通常称为动圈,未加工齿轮的则称为定圈。当回转支承转动时,定圈的每个区域与滚珠接触时的作用力不变,位于最大载荷处的滚道应力幅值最大,磨损应当最为严重,而受力较小的部分则会有轻微磨损;动圈由于其不断转动,滚道受力均匀,应力幅值在最大和最小滚道载荷之间循环,因而动圈滚道的磨损可视为均匀磨损,其磨损程度远低于定圈。所以,可用定圈的磨损程度来衡量回转支承的寿命情况。基于小样本试验的剩余寿命预测模型主要针对定圈进行研究,需要估计的参数主要是威布尔斜率和特征寿命,其流程如图1所示。
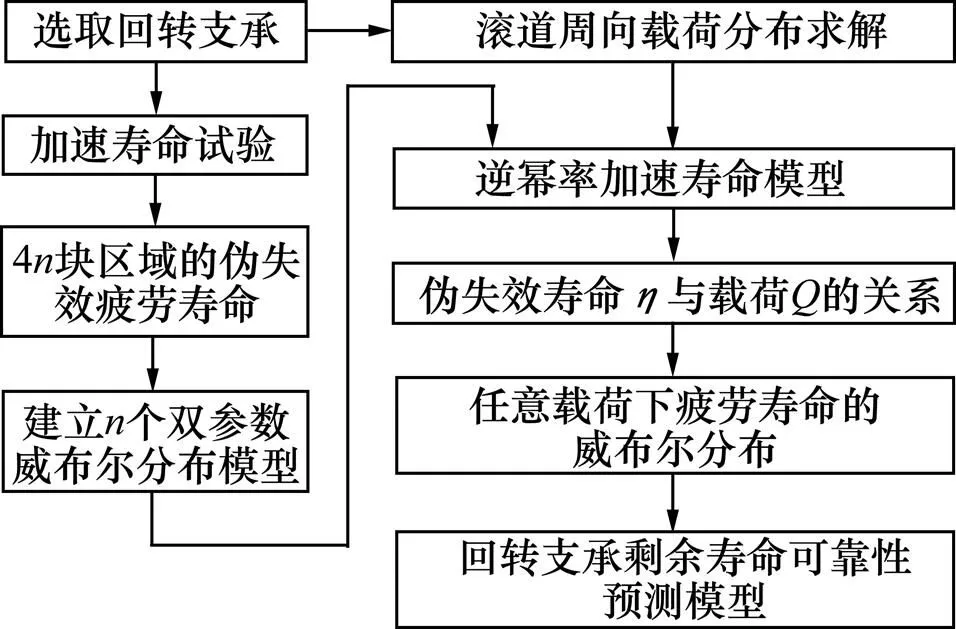
图1 剩余寿命预测模型建模过程
由图1可见:首先,根据Hertz接触等理论[14],对选取的回转支承按其设计承载能力进行滚道受载分析,由于滚道直径较大且载荷分布具有高度对称性,故可将回转支承滚道划分为4组,每组可划分成段,滚道共划分成4段;然后利用回转支承试验台进行加速寿命试验,直到回转支承失效,将失效的回转支承定圈滚道按上述方法切成4段,测量每段的体积磨损量,并利用Archard模型[9]计算出各段的伪失效疲劳寿命,以此建立组双参数的威布尔分布;最后,结合逆幂率[10]加速寿命模型,得所选回转支承载荷−疲劳寿命的关系,继而得−曲线。对于具体工况下的回转支承,可根据文献[12]所述求出滚道最大载荷,继而求得对应的特征寿命,从而建立起任意载荷下回转支承剩余寿命的预测方程。
2.1 滚道载荷分布
大型回转支承同时承受轴向力a,径向力r和倾覆力矩,其滚道的受载分布与一般轴承有所区别,Ignacio等[15−16]对此进行了深入的研究,对于4点接触的单排回转支承,其内外滚道可能同时受到滚珠的反作用力1x,1y,2x和2y,如图2所示。

图2 滚珠对滚道支反力
考虑到回转支承实际工作过程中,除了轴向旋转自由度外,其他自由度均受到约束,即所有滚珠对滚道的合力与外加载荷达到平衡,由此建立方程组
其中:为滚珠的个数;1,2和3分别为1x,1y,2x和2y在r,a和方向上合力的表达式。
由式(9)可得滚道随滚珠在0°~360°方向的载荷分布如图3所示,滚道中最大的载荷为max。

1—上滚道;2—下滚道
2.2 小样本加速寿命试验设计
为估计模型参数,通常需在不同应力水平下对试件进行批量的寿命试验,以获取足够的历史失效数据。但是,大型回转支承直径一般为0.8~5.0 m,所承受的轴向力和倾覆力达几十吨至上百吨,能满足要求的试验台很少[17−18]。而且进行一次加速寿命试验耗费的资源庞大,批量的试验从时间和经济成本方面都不可接受。因此,必须考虑通过小样本甚至单样本的试验来对回转支承剩余寿命可靠性模型进行参数估计。
小样本加速寿命试验的目的是从尽可能少的加速寿命试验中获取不同应力水平下多个回转支承的失效寿命。由图3可知:滚道的载荷分布呈一定周期性,因此可以将整个滚道分为4块区域,每块区域又可以再划分为(≥4)段。由此可得种应力水平,每种应力水平下有4段滚道,共计4段滚道样本,具体分段情况如表1所示。表1中,1,2,Q和Q为各应力水平下的平均载荷其计算公式为
其中:Q,max和Q,min分别表示各段滚道的最大和最小载荷。

表1 回转支承滚道分段
轴承的疲劳寿命试验通常是给其施加50%的极限载荷,然后以一定的转速进行。为了加快试验进 程,可以利用试验台对回转支承进行100%极限载荷的全寿命加速试验。回转支承经加速寿命试验失效后,按照表1所示将外圈切割成4段,经测量得到4段滚道的体积磨损量W(=1, 2, …, 4),其中最大的磨损量为max。由此可得,当此回转支承失效时,滚道的最大磨损量为max。即当此回转支承滚道磨损量达到max时可认为回转支承失效。为了通过一次试验获得不同载荷下滚道的失效寿命,可利用Archard磨损理论[9]:
其中:W为各段滚道的体积磨损量;Q为各段滚道所受的平均载荷;和分别为磨损系数和滑行速度,只与材料和回转支承转速有关,在此均为常量;为回转支承转过的圈数。
由式(11)可知:在载荷Q和滑动速度恒定的情况下,体积磨损量只与转过的圈数线性相关,于是可求各段回转支承运行至失效时所需的圈数t。若试验至失效时回转支承转过的总圈数为t,则
若回转支承由实际载荷计算出滚道的最大载荷为Q(=1, 2, …, 4),则由式(12)知此回转支承的伪失效疲劳寿命为t(=1, 2, …, 4)。这相当于获得了种应力水平,每种应力水平4个样本,共4个回转支承样本的疲劳失效数据。
2.3 剩余寿命模型参数估计
对回转支承进行小样本加速寿命试验后,得滚道分段及各段伪失效疲劳寿命,于是得组不同载荷下的回转支承可靠性方程:
由于不同载荷下回转支承的失效机制并没有发生变化,所以威布尔分布的形状参数β不变,因此可得石威尔布低利率的平均值为
式(13)虽建立了回转支承在个载荷下的寿命分布,但还是不能得实际中任意的载荷下回转支承疲劳寿命的威布尔分布。由实际载荷判断其寿命,需要一种模型能够表示寿命与载荷之间的关系,根据文献[10],选择反幂率寿命加速模型,即
其中:和为与材料和工况有关的参数,可根据试验结果由最佳线性不变估计法求得。
因此,对于此型号回转支承,给定实际工况并求得滚道最大载荷Q后,便可由式(15)得在Q下疲劳寿命威布尔分布下的特征寿命η,从而由式(8)和式(14)得其对应的剩余疲劳寿命可靠性预测模型为
因此,当置信度为R()时,年龄为的回转支承的剩余寿命为
3 试验验证
3.1 大型回转支承试验台
本试验使用自制的试验台[15]如图4所示。图4中1和2为双向液压缸,其组合可加载轴向力和倾覆力矩,3为单向液压缸,用以加载径向力,3者组合可模拟出回转支承的实际负载情况,利用驱动马达4以特定的速度对回转支承进行疲劳寿命试验。
试验台的参数如表2所示。
3.2 疲劳寿命试验
用某公司QNA−730−22型内齿式回转支承进行试验,其滚珠中心直径为730 mm,滚珠直径为22 mm,极限载荷为轴向力为96 kN,倾覆力矩为246 kN·m。给回转支承施以极限载荷,并以4 r/min进行全寿命的加速疲劳寿命试验。
试验台运转12 d后因回转支承卡死而停机,对应转过的圈数为6.91×104r。将回转支承进行拆解,失效的回转支承如图5所示。由图5可见:该回转支承外圈滚道磨损较为严重,局部出现大量的疲劳剥落,内圈滚道仅有部分点蚀和轻微磨损,且各处磨损均匀,与前述推断一致。此外,部分滚珠也出现磨损甚至疲劳断裂。

(a) 主视图;(b) 侧视图

表2 回转支承试验台性能参数

(a) 外圈;(b) 内圈;(c) 滚珠
按小样本加速寿命试验设计,令=4,得4种应力水平,每种应力水平有4个样本,将外圈滚道分割成16段(如图6所示)。
将切割后的滚道截面用低倍扫描电镜观察,回转支承外圈滚道截面SEM图如图7所示。由图7可知:与未经试验的滚道进行对比,试验后滚道出现大幅不均匀的磨损。
因此,对各段回转支承采用OLYMPUS9体视显微镜进行观察,并用Q−capture pro成像系统和驱动及分析软件进行磨痕宽度位置和深度分析,得各段回转支承体积磨损量W(=1, 2, …, 16),如图8所示。
3.3 数据处理与讨论
从图8可以看出:第4段和第5段滚道磨损速率超出正常趋势范围,由于这2段滚道处于软带区域,是热处理工艺的交界处,次表面硬度比滚道其他部位低,因而出现较快的磨损和较低的失效寿命,应予以剔除。由此,可得4种应力水平下的回转支承疲劳寿命威布尔分布:
其中:η和β取值如表3所示。

图6 回转支承外圈切割示意图

图7 回转支承外圈滚道截面SEM图

1—体积磨损量;2—拟合曲线
由图8可知:当回转支承失效时,外圈滚道最大的体积磨损量为2.264 mm3,以此为阈值,由式(12)得其他15段滚道的伪失效疲劳寿命如表4所示。
十九世纪以来,随着科学技术的高速发展,金属材料的消耗与日俱增,传统金属矿产资源的日益枯竭及世界能源与环境等问题的日益突出,因此对材料的使用提出了更高的要求.镁合金因在轻量性、比强度、比刚度、导热导电性、阻尼减震性、加工成型性、电磁屏蔽性及可回收性等方面具有独特的优势,受到了越来越多的关注,而广泛应用于航空、军事、交通及3C领域中[1-3].由于雷达外壳在整个雷达系统中占有重要位置,其质量的好坏直接影响着信号探测的灵敏度.选用AE44稀土镁合金做雷达外壳材料,在起到轻量化作用的同时,其优异的强度和韧性可满足雷达外壳的工作要求.

表3 各应力水平下的ηm和βm
由式(14)可得威布尔斜率的平均值mean=18.735,由式(15)对4组应力水平下的威布尔分布进行拟合,利用最佳线性不变估计法得
由此可得本回转支承在90%置信度下的载荷−疲劳寿命曲线,与 NREL[11]和ISO281[12]中的10计算结果的对比如图9所示。
由图9可以看出:NREL推荐的10计算结果与ISO281较为相似,但NREL计算结果稍大,可能是NREL计算当量动载荷a为理论计算出的滚道载荷, ISO281的a为经验系数乘以实际外部载荷,通常经验系数都会考虑一定的安全因素,导致求得的当量动载荷偏大,从而使疲劳寿命10偏小。另外,当外部载荷较小时,NREL和ISO281计算所得疲劳寿命均大于提出模型的计算结果,而外部载荷超过50%设计载荷时,情况刚好相反。实际上,试验中的回转支承利用ISO281计算其疲劳寿命应为7 d,而试验12 d后回转支承才疲劳失效,说明本方法的结果更接近工程实际。回转支承通常在低速重载工况下工作,因此,本方法不仅具有一定的实用性,还可避免企业过早地更换仍然能够正常服役的回转支承,为企业提供参考。
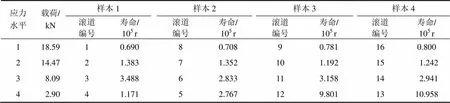
表4 16段滚道的伪失效疲劳寿命

1—NREL;2—本文方法;3—ISO281
因此,对于试验中的回转支承,若在50%极限载荷下工作,滚道最大载荷为9 293 N,由式(19)得=2.480×105,=18.735。因此,在50%极限载荷下,年龄为的回转支承的剩余寿命可靠性模型为
图10所示为此工况下,使用年龄为0.9×105,1.0×105,1.2×105,1.8×105,2.0×105,2.2×105和2.3×105r的回转支承剩余寿命曲线。
由图10可以看出:回转支承已运行时间越长,在80%置信度以上的剩余寿命可靠性曲线越陡,说明可靠性下降越快,剩余寿命越短;而使用时间越短,曲线分散性越大,越接近原始的威布尔分布。
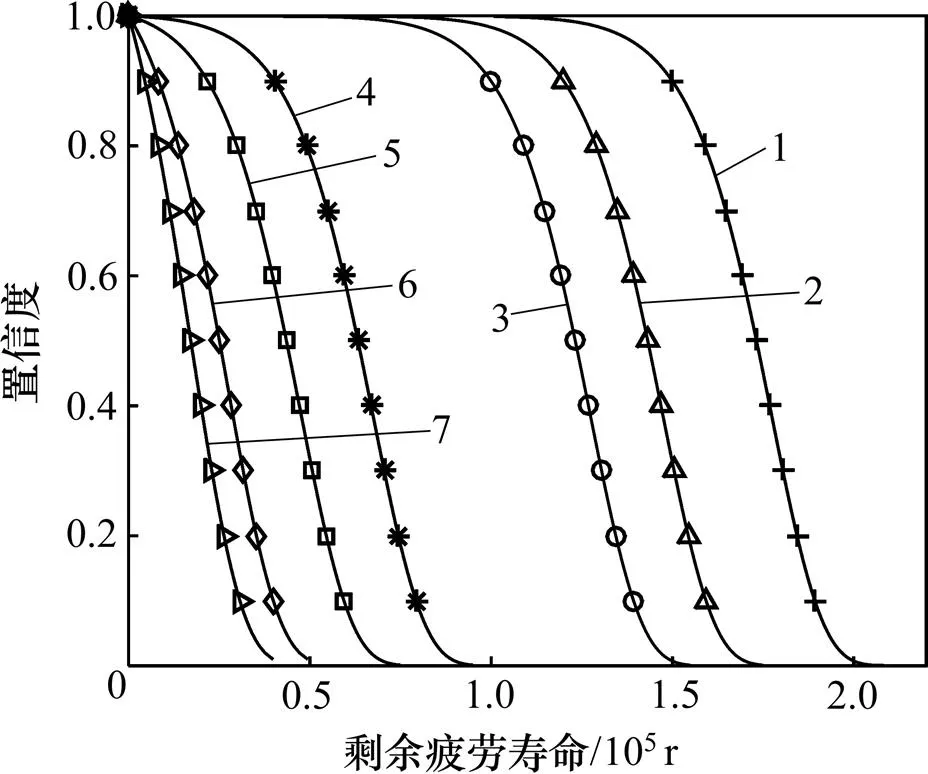
t/105 r: 1—0.9; 2—1.0; 3—1.2; 4—1.8; 5—2.0; 6—2.2; 7—2.3
4 结论
1) 提出一种通过小样本加速寿命试验进行回转支承剩余寿命预测的可靠性模型,包含基于威布尔分布的剩余寿命模型,以及模型参数估计的方法,该方法能以较小的试验成本和时间建立起回转支承的寿命模型。
2) 此方法利用回转支承滚道载荷分布特点,通过一次加速疲劳寿命试验,可同时获得多个应力水平下多个样本的回转支承滚道寿命的分布。相比传统的可靠性建模方法,大大节省试验成本,而且此方法还可应用到其他类似的大型低速重载运转部件的可靠性建模中。
3) 本方法通过一次试验即可建立回转支承在任意载荷下的整个寿命周期的可靠性模型,适时地为操作人员提供维护、更换的规划,既避免不必要的过度维护,又能降低事故的发生。
4) 用某公司的回转支承的试验验证结果表明:回转支承滚道的寿命随载荷的分布情况符合建模时使用的威布尔分布。结合实际工况并与NREL和ISO 281提供的10计算方法相比,本文的寿命预测结果可有效避免用户过早对回转支承进行不必要的维护或更换,从而为企业节约更多资源。同时,本方法也可对同一回转支承中不同位置处的滚道进行寿命分析,可以为产品的设计和维护提供参考。
[1] Kim H E, Tan A C, Mathew J, et al. Bearing fault prognosis based on health state probability estimation[J]. Expert Systems with Applications, 2012, 39(5): 5200−5213.
[2] Benkedjouh T, Medjaher K, Zerhouni N, et al. Remaining useful life estimation based on nonlinear feature reduction and support vector regression[J]. Engineering Applications of Artificial Intelligence, 2013, 26(7): 1751−1760.
[3] Medjaher K, Tobon-Mejia D A, Zerhouni N. Remaining useful life estimation of critical components with application to bearings[J]. IEEE Transactions on Reliability, 2012, 61(2): 292−302.
[4] 张慧芳, 陈捷. 大型回转支承故障信号处理方法综述[J]. 机械设计与制造, 2012, 3(3): 216−218. ZHANG Huifang, CHEN Jie. Reserch on signal processing method of large slewing bearings[J]. Machinery Design & Manufacture, 2012, 3(3): 216−218.
[5] Potočcnik R, Flašker J, Glodez S. Fatigue analysis of large slewing bearing using strain-life approach[C]// 12th International Conference on Fracture. Ottawa, Canada, 2009: 3891−3898.
[6] Potočnik R, Göncz P, Flašker J, et al. Fatigue life of double row slewing ball bearing with irregular geometry[J]. Procedia Engineering, 2010, 2 (1): 1877−1886.
[7] Potočnik R, Göncz P, Glodez S. Lifetime determination of the raceway of a large three-row roller slewing bearing[J]. Key Engineering Materials, 2012, 488: 113−116.
[8] GAO Xuehai, HUANG Xiaodiao, HONG Rongjing, et al. A rolling contact fatigue (RCF) reliability evaluating method[J]. Journal of Tribology, 2012, 134(1): 1−7.
[9] Halling J. Principles of tribology[M]. London: McMillan, 1975: 378−392.
[10] 茆诗松, 王玲玲. 加速寿命试验[M]. 北京: 北京科学出版社, 2000: 138−143. MAO Shisong, WANG Lingling. Accelerated life test[M]. Beijing: Science Press, 2000: 138−143.
[11] Harris T, J Rumbarger, Butterfield C. Wind turbine design guideline—DG03: Yaw & pitch rolling bearing life[R]. Washington DC: National Renewable Energy Laboratory, 2009: 10−15.
[12] ISO 281, Rolling bearings—Dynamic load ratings and rating life[S].
[13] Ernest Y R. A universal bivariate Weibull model for static and dynamic fatigue reliability forecasting[C]// 2011 ASTM International Symposium on Rolling Element Bearings. Altadena, United States, 2012, 1542: 26−46.
[14] Harris T, Kotzalas A M. Rolling bearing analysis[M]. 5th ed. New York: Taylor & Francis Group, 2006: 98−101.
[15] Ignacio A J, Xabier S, Jorge D. Load distribution in a four contact-point slewing bearing[J]. Mechanism and Machine Theory, 2003, 38(6): 479−496.
[16] GAO Xuehai, HUANG Xiaodiao, WANG Hua, et al. Load distribution over raceways of a 8-point-contact slewing bearing[J]. Applied Mechanics and Materials, 2010, 29(32): 10−15.
[17] 黄筱调, 王华, 陈捷, 等. 风电转盘轴承综合性能实验台: 中国, CN100587444C[P]. 2010−02−03.HUANG Xiaodiao, WANG Hua, CHEN Jie,et al. Test rig for slewing bearings used in wind turbines: China, CN100587444C [P]. 2010−02−03.
[18] Zvokelj M, Zupan S, Ivan P. Multivariate and multiscale monitoring of large-size low-speed bearings using ensemble empirical mode decomposition method combined with principal component analysis[J]. Mechanical Systems and Signal Processing, 2010, 24(4): 1049−1067.
(编辑 刘锦伟)
Residual life prediction of large-size slewing bearings based on small-sample test
FENG Yang, HUANG Xiaodiao, CHEN Jie, WANG Hua, HONG Rongjing
(School of Mechanical and Power Engineering, Nanjing Tech University, Nanjing 210009, China)
A residual life prediction approach for slewing bearings was proposed based on a small-sample test. Firstly, a residual life prediction model for slewing bearings was established based on modified Weibull distribution. Then, the load distribution over the slewing bearing raceway was analyzed on the basis of Hertz’s theory. Afterwards, a new method for Weibull parameters estimation was proposed based on a small-sample test, which utilized the Archard theory and the Anti-power acceleration life model. Finally, an experiment was conducted on an inner-geared slewing bearing (QNA−730−22) to verify the proposed approach. The results show that the fatigue life distributions of multiple samples in multiple load cases can be determined through one life-cycle experiment, and that the proposed approach is closer to engineering practice compared with the NREL design guide and the ISO 281. Besides, the modeling procedure of the proposed method is efficient and time-saving, and all the merits of the method provide a potential for enterprises in making timely proactive maintenance schedules.
Weibull distribution; slewing bearing; life prediction; small-sample test
10.11817/j.issn.1672-7207.2015.09.013
TH136
A
1672−7207(2015)09−3252−08
2014−09−27;
2014−12−11
国家自然科学基金资助项目(51375222,51175242) (Projects(51375222, 51175242) supported by the National Natural Science Foundation of China)
黄筱调,教授,博士生导师,从事先进数控理论及设备健康监测研究;E-mail: njgdhxd@yeah.net

