求解动态优化问题的改进多种群引力搜索算法

毕晓君，刁鹏飞，王艳娇，肖婧



求解动态优化问题的改进多种群引力搜索算法

毕晓君1，刁鹏飞1，王艳娇2，肖婧3

(1. 哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨，150001;2. 东北电力大学信息工程学院，吉林吉林，132012;3. 辽宁省交通高等专科学校信息工程系，辽宁沈阳，110122)

针对目前多种群算法解决动态优化问题时存在过多冗余计算、寻优精度低等缺陷，提出多种群串行搜索的引力搜索算法。采用多种群串行搜索的策略，便于当前子种群利用其他已收敛种群的进化信息。为解决多峰重复搜索而带来的冗余计算问题，提出具有约束条件的初始化策略，给予初始化的粒子以方向性的指引，避免其初始化在已寻峰区域；采用距离判决的策略发现并终止多峰重复搜索。为全面的监测环境变化及解决多样性丢失问题，提出一种监测环境策略及追踪策略。研究结果表明：所提算法，面对不同的环境变化程度以及不同的峰值数量，其求解精度都优于其他7种对比算法的求解精度，证明该算法在求解动态优化问题上的优越性。

引力搜索算法(GSA)；动态优化问题(DOPs)；多种群策略

近年来，对智能优化算法的研究主要集中在求解不随时间变化的静态优化问题上[1]。然而，实际工程中的多数问题都是动态优化问题(dynamic optimization problems, DOPs)，如市场波动或金融变化等，因此DOPs的研究具有实际意义。DOPs问题的约束条件、目标函数和解会随着时间或其他参数发生变化，对于DOPs问题来说，求解目标已不再是寻得最优解，还要求算法可以检测到环境的变化、解决多样性丢失并尽可能地动态的追踪最优解。典型的智能优化算法如粒子群算法[2−3]、差分进化算法[4]等作为解决动态优化问题的基础算法，虽表现出良好的搜索能力，但在面临多种环境变化的问题，其求解精度仍有待提高。同时，面对多样性缺失、环境动态变化等问题，采取何种策略与优化算法相结合也是决定算法性能的关键。目前常见的辅助策略主要有：环境变化后增加多样性、始终保持多样性、记忆策略与多种群策略 等[5]。其中，多种群策略是目前被广泛采用的解决DOPs的策略，该策略的核心思想是通过多个子种群并行的搜索各个局部最优峰，当环境变化时，在给出所得最优值的同时，各子种群继续追踪局部峰的变化。但该策略容易出现多个种群同时搜索1个局部峰的情况，增加了计算开销，对此，Blackwell等[6]提出了一种根据距离判断重复搜索的策略，该策略虽能及时地判断出多子群重复搜索，但带来了较高的计算复杂度，且因多子群重复搜索而带来的计算开销仍有望进一步减少。引力搜索算法(gravitational search algorithm, GSA)是2009年提出群智能优化算法，具有设置参数少、全局搜索能力强、计算简单、收敛速度快等优点[7]。目前关于GSA的研究主要集中在静态优化问题上，国内外针对DOPs的研究还较少。本文作者通过对现有的多种群策略进行改进，并根据GSA自身特点提出一种基于改进多种群的引力搜索算法，采用多种群串行搜索策略，有利于各种群充分共享彼此进化过程中得到的信息；采用排斥距离策略以使粒子带有约束条件的初始化，一定程度上避免粒子初始化在已寻峰所在区域，提高粒子的进化价值；采用距离判决策略可以及时发现当前种群是否正在搜索已寻峰，减少计算开销；采用一种环境检测策略，及时全面的检测出各个峰的变化情况；采用一种针对已寻峰的追踪策略，提高算法的搜索效率。最后，通过动态标准测试问题，对主要参数进行研究分析，并与目前解决DOPs问题效果较好的7种算法相比较，验证本文算法的有效性和先进性。

1 引力搜索算法基本原理

在GSA中，种群个体都是在空间中运动的个体，它们在万有引力的作用下彼此相互吸引运动，它们的质量大小是评价其优劣的标准，质量较大粒子的位置对应较优解。在进化过程中，GSA算法通过个体间的万有引力相互作用实现优化信息的共享，引导群体向最优解区域运动展开搜索。

若空间中含有个粒子，则第个粒子的位置为

其中：=1, 2, …,；为搜索空间的维数；为第个粒子在第维上的位置信息。在时刻，2个粒子间的作用力为

其中：M()和M()分别为粒子和粒子的质量；为一个极小的常量；()为在时刻的万有引力常数。具体定义为

其中：0为初始时刻的引力常数；为最大迭代次数，且设置不同的会导致引力常数以不同的趋势减小。若R()为粒子与粒子之间的欧氏距离，则在时刻，粒子在维上受到的其他粒子的合力为

其中：r为变化区间在[0, 1]之间的随机数；为粒子对粒子在第维空间上的作用力。依据牛顿第二定律，定义时刻粒子在维上的加速度为

在进化过程中，粒子的速度和位置的更新方式为

粒子的质量与其适应度值有关，质量越大的粒子，表明其更接近最优粒子，其对其他粒子的作用力会较大但是其移动速度会较慢，粒子质量的计算公式为

(7)

其中：f()为粒子的适应度；()为质量最小粒子的适应度；()为质量最大粒子的适应度。

2 基于改进多种群策略的引力搜索算法

通过分析传统多种群策略在解决动态优化问题上存在的不足，对多种群策略的种群搜索模式进行改进，并根据动态优化问题的特点，提出一种基于改进多种群策略的引力搜索算法。

2.1 改进多种群策略

2.1.1 多种群串行搜索

多种群策略是目前被广泛采用的解决动态优化问题的一种策略，其基本思想是多个子种群共同对最优解展开搜索并分享彼此在进化过程中所得到的进化信息，当发现环境变化时输出最优值，然后利用多个子种群继续的追踪这些已寻峰，以达到动态寻优的目的。这是一个多种群并行进化搜索的过程，然而多种群同时展开搜索容易出现多个子种群同时搜索同一个峰的问题，这无疑会增加许多计算开销，降低算法的寻优效率。因此根本上的解决重复搜索问题是多种群策略能有效解决动态优化问题的关键。

对此，许多学者都提出了改进策略，其中最具代表性的是Blackwell等[6]采用比较各种群最优值距离的方法，判断各个子种群所寻最优值是否相同，判决阈值定义为

其中：为搜索空间；为局部峰值的个数；为问题的维数；excl为判断重复搜索的阈值。若当前子种群的最优粒子与某个已寻局部峰之间的欧氏距离小于阈值excl时，判定当前种群所优化的区域已被其他种群开采过，则终止最优值较差的那个子群的继续搜索。

该策略虽然能判断出多个子种群重复搜索，在一定程度上降低了种群重复搜索同一个峰所带来的效率低下的影响，但每次迭代搜索都需要计算各个子种群所寻最优粒子之间的距离，这会增加较多的计算复杂度；另外，当较多子种群都同时搜索同一个峰时，重新初始化这些子种群仍会增加许多的计算开销，这会降低算法优化动态问题的整体性能。

因此，为解决现有多种群策略存在重复搜索的问题，本文在原有多种群策略的基础上，提出一种改进的多种群策略，即将原有多个种群同时对解空间优化搜索，改进为各个子种群依次优化搜索最优解，并在优化的过程中，采用文献[6]所述方式监测子种群是否发生重复搜索的情况，这种改进的多种群策略相比于现有多种群并行搜索策略的优势是：1) 重复搜索最多只会发生在2个子种群之间，一旦判断出子种群重复搜索时，只需要重新初始化1个子种群，这节省了较多计算开销；2) 只需计算当前种群与其他已寻峰之间的欧式距离，减小了计算复杂度。

2.1.2 收敛判决策略

本文提出的改进多种群搜索策略，是多个子种群按顺序搜索解空间，当1个子种群收敛时，再初始化1个新子群，因此需要为每个种群设定收敛的条件。而当种群逐渐收敛时，则种群的多样性会逐渐降低，并由此而导致当前最优粒子与种群中的其他粒子在各个维度上的差异度也随之降低，因此，可以通过种群当前最优粒子与其他粒子在各个维度上整体的差异度来判断种群的收敛情况。基于此思想，本文提出一种判断收敛的方式，具体为

其中：为问题的维数；Gbestj()为在时刻种群所搜寻的最优个体在第维上的位置信息，rj()为在时刻，除最优个体Gbestj()外，种群中其他个体在第维上的位置信息的平均值；l为判决阈值。如果l较大，则收敛程度不是很高的种群会符合收敛条件，这会导致寻优精度的降低；当l较小时，虽然种群会得到精度较高的解，但随着收敛程度的不断提高，寻优结果在精度上提高的幅度会越来越不明显，而且还会增加子种群完成1次寻优的计算开销，这会降低算法整体的优化效率，因此l需要平衡对单个解的开采精度及计算开销之间的关系。通过实验比较，当l为0.01时，算法性能最好。

当1个种群符合收敛条件时，则说明当前种群最优粒子与其他粒子在各个维度上的差异度较小，此时种群已收敛，记录当前所寻值，并重新初始化1个新种群继续搜索最优解。

2.1.3 带有约束条件的初始化策略

对于多种群串行的搜索策略，当判定1个子种群收敛时，记录该子群所得峰值并重新初始化1个新的子群，然而随机初始化的粒子有可能生成在已寻峰所在区域，特别是随着已寻峰数量的增多，这种可能性会逐渐增加。对于依靠粒子间的相互作用力进行优化的GSA来说，随着进化的进行，这些初始化在已寻峰周围的粒子，极有可能在力的作用下吸引其他粒子进入已寻峰所在区域，进而导致该子群重复搜索已寻峰，因此，为了防止子群重复搜索已寻峰，需要给予初始化的粒子一定方向上的指引。通过以上分析，本文提出一种带有约束条件的种群初始化方式来指引粒子的生成，约束条件为

其中：X()为粒子在时刻的位置信息；为第次环境下已寻峰的位置信息；为粒子与已寻峰之间的欧氏距离；为约束距离，即当前初始化粒子与任何一个已寻峰相互间的距离小于时，粒子极可能陷入了已寻峰所在的区域，此时重新初始化该粒子以得到搜索价值更高的粒子。通过实验比较，当为70时算法性能达到最优，若过大，约束距离较大会使粒子错过一些未寻峰值所在的区域，则会增加对这些未寻峰的搜索难度；若较小，则不能达到跳出已寻区域的目的。当1个子种群达到收敛条件时，采用带有约束条件的初始化方式生成新种群，可以提高初始化粒子的进化价值，利于对其他未寻峰展开搜索，提高了整体的搜索效率。

2.2 环境监测与追踪

2.2.1 环境监测策略

智能优化算法对问题的优化过程实际上是种群逐渐收敛的过程，其多样性会逐渐下降。而对于动态优化问题，当环境发生变化时，已收敛的种群因其多样性降低而不再具有开采新解的能力。因此，算法需要具有检测环境变化的能力，以及时的更新存储的诸如已寻峰等相关信息。

为了达到检测环境的目的，目前采取的环境检测方式主要有哨兵法[8]和最优值变化法[9]，这2种方式都是通过比较某个粒子前后代值的变化情况来检测环境的，无法准确的判断出哪些局部峰发生了变化。基于以上分析，为了准确的判断出整体环境的变化情况，本文采取的检测策略描述如下：

1) 每隔代，比较各个已寻峰的变化情况。

2) 当有某个已寻峰发生变化时，则此时环境发生变化，输出已寻峰中的最优值。

3) 对于未变化的峰，则将其视为环境变化后的已寻峰。

其中：对于参数的取值，若设置过大，则会延误环境变化后被检测出来的时间，若设置过小，则会增加额外的计算开销。通过实验比较，当为10时算法性能可以达到最优。这种检测策略，一方面能及时准确的判断出环境的变化；另一方面，将未变化的峰直接作为下一代已寻峰，减少了待寻峰的个数，提高了算法的整体搜索效率。

2.2.2 追踪策略

对于DOPs问题，当环境发生变化时，虽然各个局部峰会出现不同程度的变化，但并不是完全随机的重新生成新的峰，其变化在一定的范围内可追踪。在本文中，将环境变化前被种群搜寻到，且随环境发生变化的峰称为待追踪峰。

当环境变化时若初始化的粒子在待寻峰周围生成，则会加快种群对该峰的搜索速度，提高算法的搜索效率。因此，为了准确的追踪各个局部峰，本文采用下式方式初始化粒子。

其中：为变化区间在[0, 1]之间的随机数；X()为随机产生的第个粒子在维上的信息；X为第个已寻峰在第维上的信息；为控制粒子生成区间的参数。

在种群追踪待追踪峰的过程中，若能缩小待搜索区域，则会提高搜寻待追踪峰的效率，因此希望参数越小越好。然而，若搜寻区域设置过小，则可能导致待追踪峰种群的追踪。通过实验比较，当参数为3时，算法会获得更好的优化效果。

通过在待追踪峰周围随机生成的方式追踪峰值的变动，大大缩小算法对最优解的搜索区域，减少了对最优解的搜索时间，提高了优化搜索的效率。当完成对所有待追踪峰的追踪后，若仍未检测出环境变化，则采用具有约束条件的种群初始化策略，继续对解空间展开搜索。

2.3 所提算法主要过程

1) 种群初始化，设置种群规模为，排斥距离，判断种群是否收敛的阈值l，以及参数。

2) 初始化1个种群并对解空间展开搜索，当种群满足式(9)时，则种群收敛，记录当前种群的最优值。

3) 按式(10)所示约束条件初始化1个新种群。

4) 在每个种群搜索最优解的过程中，通过式(8)判断当前种群是否搜寻的是已被寻到的峰。

5) 采用2.2.1所述方式检测环境的变化，当检测到环境变化时，输出环境变化前一刻所寻到的全局最优值。

6) 当环境变化后，根据各个已寻峰的变化情况，对各个已寻峰进行分类，若峰值未发生变化，则将其作为环境变化后的已寻峰处理；若该峰发生变化，则采用2.2.2所述的追踪策略，追踪这些峰。

7) 当采用追踪策略完成对所有待追踪峰的优化搜索后，种群初始化策略仍采用带有约束条件的初始化方式。

3 仿真实验与结果分析

所有实验在硬件配置为Intel® Core™2 Duo CPU P7570 2.26 GHz、2 G内存、2.27 GHz主频的计算机上进行，开发环境为Matlab2010.b。

3.1 测试问题

本文采用目前国际上较为权威的移动峰问题(moving peaks benchmark，MPB)[10]来对算法进行测试，该测试问题的特点是周期性的改变峰的高度、宽度和移动峰的位置以构造复杂的动态环境，测试问题的目标函数为

其中：W()和H()分别为第个局部最优峰在时刻的宽度和高度；X()为第峰在维上的位置信息。MPB的相关参数如表1所示。通过比较离线误差和标准方差来比较算法性能，离线误差的公式为

其中：为环境变化次数；h为理论最优值；f­为第次环境变化前的算法所寻最优值。

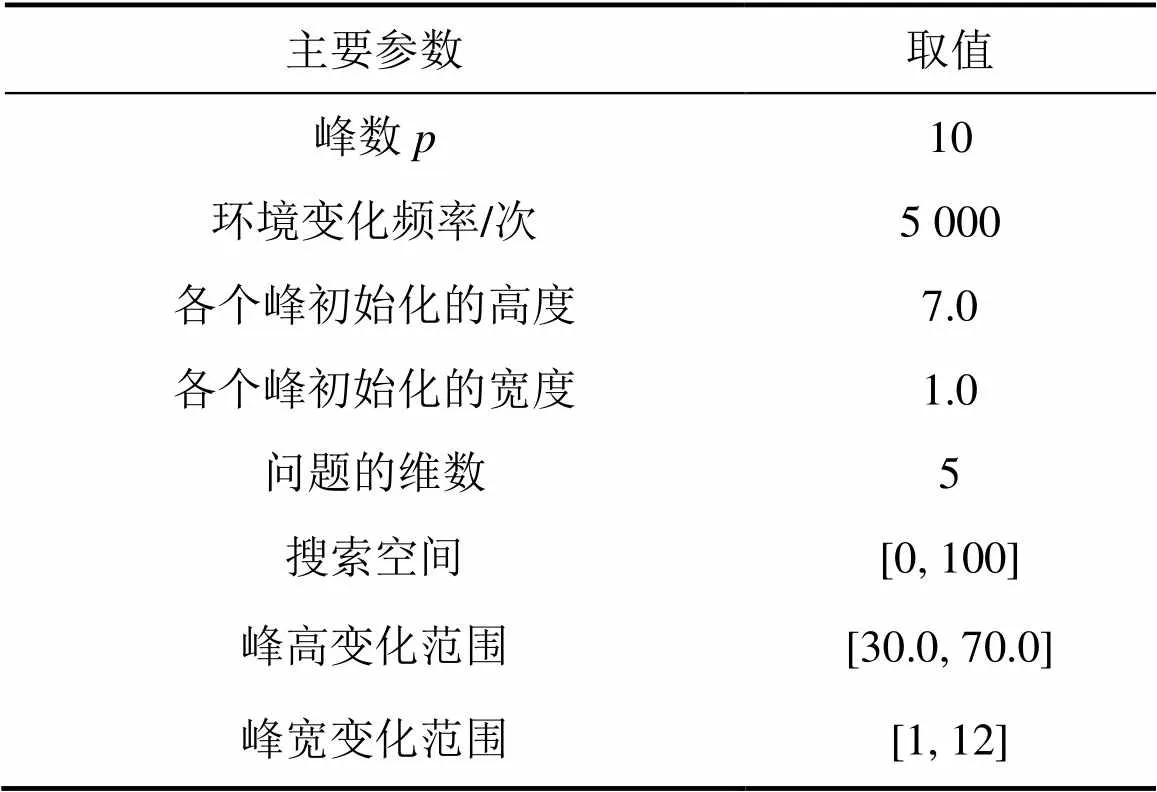
表1 MPB问题参数设置

3.2 实验设置

采用2组实验研究多种群引力搜索算法在解决动态优化问题上的性能。第1组实验主要分析关键参数对于算法整体性能的影响。第2组实验是比较多种群引力搜索算法与目前解决动态优化问题效果较好的7种算法，7种算法分别为：CDDE_Ar[4]，FTMPSO[11]，jDE[12]，CPSOR[13]，Dopt-aiNET[14]，CPSO[8]和PSO-CP[15]。对于引力搜索算法的相关参数设定参考文献[6]，种群规模取10，阈值l取0.01，排斥距离取80，取3，环境变化次数取100次。所有仿真实验都独立运行20次。

3.3 参数分析

3.3.1参数的研究

在GSA中，如式(3)所示，需要为引力常数设置合适的变化趋势，也即对参数的设置。本组实验目的是研究参数对算法性能的影响，实验结果如表2所示。从表2可以看出：当为150时，离线误差最小，算法所得到的求解精度最高；当参数大于150时，算法性能会逐渐下降。这是因为当较大时，则引力常数()变化较缓，进而导致进化步长变化较慢，虽然能使种群更加精细的对解空间展开搜索，但是会增加单个种群搜索的计算量，减少种群的搜索次数，降低算法整体的优化性能；当较小时，()变化较快，使得进化步长变化较快，进而导致种群收敛到非局部最优峰上，降低了算法的搜索能力。

3.3.2 种群规模的研究

本组实验目的是研究不同的种群规模对算法优化性能的影响，取种群规模，实验结果如表3所示。从表3可以看出：当种群规模设置为10时，会得到较好的实验结果。当种群规模较小时，由于种群多样性较低，种群搜索最优解的难度加大，使得算法的整体优化性能下降；而当种群规模设置较大时，则会增加种群单次搜索的计算量，会减少种群的搜索次数，降低算法的整体优化性能。

表2 参数T研究结果

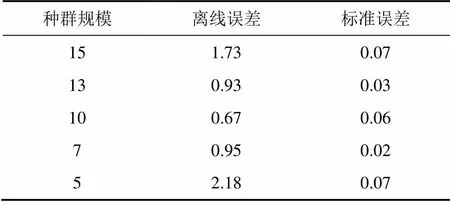
表3 种群规模的研究结果

3.4 与其他算法的对比

3.4.1 不同动态程度DOPs的比较

为了考察在不同的环境变化强度下，比较所提算法与其他目前解决动态优化问题效果较好的7种算法，结果如表4所示，从表4可以看出：随着环境变化强度的增加，各算法的求解精度在一定程度上都会有所下降，这是因为环境变化越来越剧烈，加大了算法跟踪全局最优解的难度。但所提算法在不同的变化强度下，精度和稳定性都优于其他的7种算法的精度和稳定性。这是因为多种群策略、带有约束条件的初始化策略及重复搜索监测策略为优化节约了大量的计算成本，进而增加了初始新子种群的次数，使最优解有更多的机会被开采到，当环境监测策略及时全面的检测到环境的变化后，追踪策略又保证了对已寻峰的追踪。另外，如果环境变化程度较大，个别已寻峰脱离种群追踪，那么多种群串行搜索的策略又能继续的追踪到该峰。

3.4.2 不同峰值DOPs的比较

考察所提算法与其他7种算法，在解决不同峰值数量的动态问题上的性能对比，实验结果如表5所示，从表5可以看出：随着局部最优峰数量的逐渐增多，各个算法性能都有不同程度的降低，这是因为随着峰值数量的增加，在有限的计算成本下，算法搜寻到最优解的难度加大。本文所提算法相比于其他7种对比算法在解决不同峰值数量的动态优化问题时，表现出明显的优势。这是因为本文算法一方面减少了因重复搜索带来的计算开销，另一方面，及时全面的检测环境的变化并采取相应的追踪策略，缩小了随时间变化的局部峰的搜索区域，GSA快速的搜索速度又进一步减少了搜寻峰值所需的计算开销。

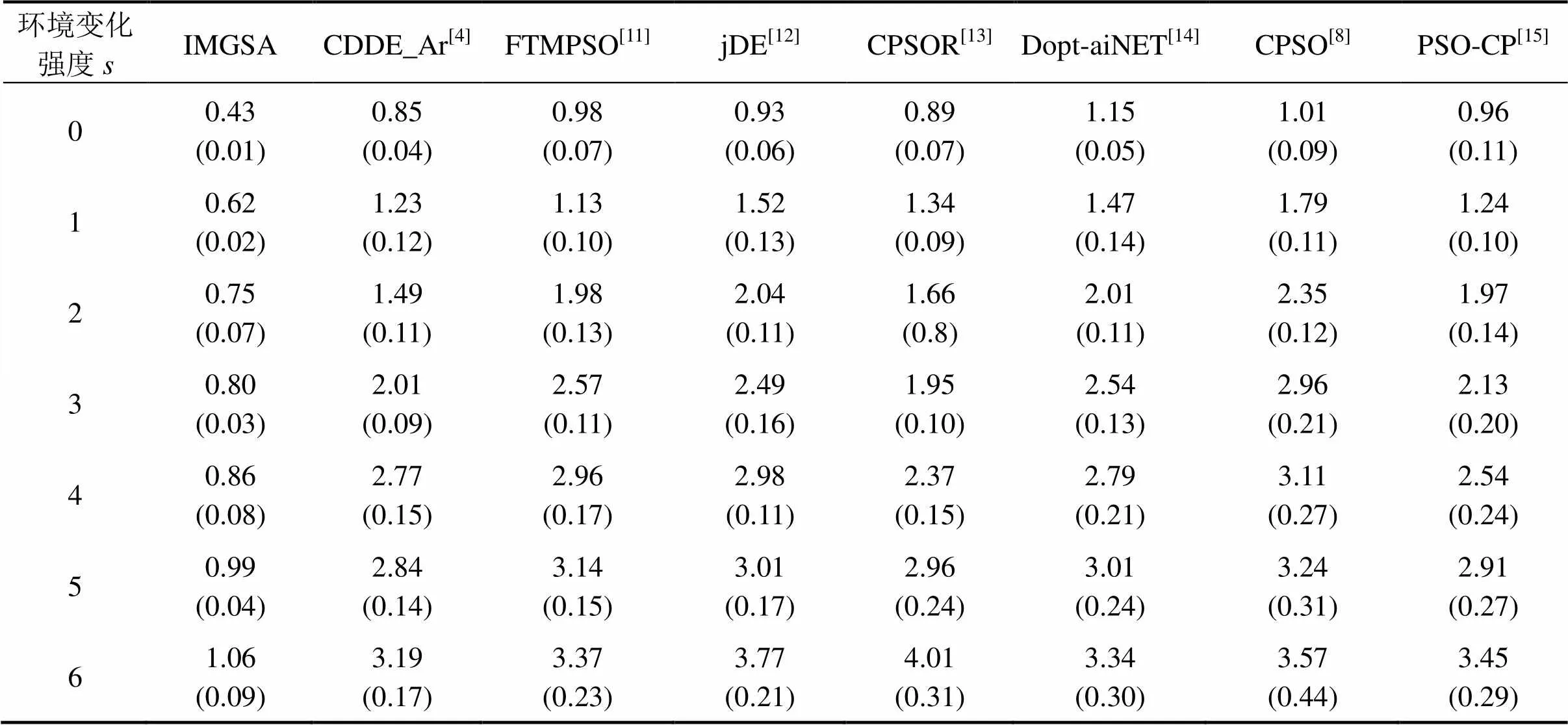
表4 IMGSA与其他7种算法在不同环境变化强度下实验对比

注：括号内的数据为标准误差；括号外的数据为离线误差。

表5 IMGSA与其他7种算法在不同峰数下实验对比

注：括号内的数据为标准误差；括号外的数据为离线误差。

通过对仿真结果的分析可知：IMGSA算法与其他7种算法相比，在解决不同的环境变化程度及不同峰值数量问题时，均表现出较好的寻优性能，表明了本文算法在解决DOPs问题上的优越性。

4 结论

1) 提出了一种基于改进多种群策略的引力搜索算法。该算法采用多个种群串行搜索的方式，共享种群间的进化信息；采用带有约束条件的初始化策略给予初始化粒子方向性的指引；采用监测种群重复搜索的策略，减少了重复搜索同一个峰而带来的冗余计算；采用一种环境检测策略，在及时检测环境变化的同时，全面的掌握了各个峰值变化的具体情况，对于未变化峰予以保留；采用一种追踪策略，准确追踪各个已寻峰的变化。

2) 找出了最适合的算法进化步长变化的趋势，提高了算法的求解精度。本文提出的IMGSA算法较现有的多种动态优化算法在不同峰值、不同环境变化程度下，其寻优精度均优于其他多种动态优化算法寻优精度，在解决动态优化的实际问题中具有广泛的应用价值。

[1] 施荣华, 朱炫滋, 董健, 等. 基于粒子群−遗传混合算法的MIMO雷达布阵优化[J]. 中南大学学报(自然科学版), 2013, 44(11): 4500−4505. SHI Ronghua, ZHU Xuanzi, DONG Jian, et al. A hybrid approach based on PSO and GA for array optimization in MIMO radar[J]. Journal of Central South University (Science and Technology), 2013, 44(11): 4500−4505.

[2] 朱庆保, 徐晓晴, 朱世娟. 一种新的求解动态连续优化的分层粒子群算法[J]. 控制与决策, 2013, 28(10): 1573−1577. ZHU Qingbao, XU Xiaoqing, ZHU Shijuan. A new hierarchical PSO algorithm for solving dynamic and continuous optimization problems[J]. Control and Decision, 2013, 28(10): 1573−1577.

[3] 高平安, 蔡自兴, 余伶俐. 一种基于多子群的动态优化算法[J]. 中南大学学报(自然科学版), 2009, 40(3): 731−736. GAO Pingan, CAI Zixin, YU Linli. Multi-swarm based optimization algorithm in dynamic environments[J]. Journal of Central South University (Science and Technology), 2009, 40(3): 732−736.

[4] Halder U, Das S, Maity D. A cluster-based differential evolution algorithm with external archive for optimization in dynamic environments[J]. IEEE Transactions on Cybernetics, 2013, 43(3): 881−897.

[5] Zuo X, Xiao L. A DE and PSO based hybrid algorithm for dynamic optimization problems[J]. Soft Computing, 2014, 18(7): 1405−1424.

[6] Blackwell T, Branke J. Multiswarms, exclusion, and anti- convergence in dynamic environments[J]. IEEE Transactions on Evolutionary Computation, 2006, 10(4): 459−472.

[7] Rashedi E, Nezamabadi-Pour H, Saryazdi S. GSA: A gravitational search algorithm[J]. Information Sciences, 2009, 179(13): 2232−2248.

[8] YANG Shengxiang, LI Changhe. A clustering particle swarm optimizer for locating and tracking multiple optima in dynamic environments[J]. IEEE Transactions on Evolutionary Computation, 2010, 14(6): 959−974.

[9] 刘黎黎, 李国家, 汪定伟. 动态环境下带有非线性效应的复合粒子群优化算法[J]. 控制理论与应用, 2012, 29(10): 1253−1262. LIU Lili, LI Guojia, WANG Dingwei. Composite particle swarm optimization with nonlinear effect in dynamic environment[J]. Control Theory & Applications, 2012, 29(10): 1253−1262.

[10] Branke J. Memory enhanced evolutionary algorithms for changing optimization problems[C]// Proceedings of the 1999 Congress on Evolutionary Computation-CEC99. Washington, DC, United S tates: IEEE, 1999: 1875−1882.

[11] Yazdani D, Nasiri B, Sepas-Moghaddam A, et al. A novel multi-swarm algorithm for optimization in dynamic environments based on particle swarm optimization[J]. Applied Soft Computing, 2013, 13(4): 2144−2158.

[12] Brest J, Zamuda A, Boskovic B, et al. Dynamic optimization using self-adaptive differential evolution[C]// 2009 IEEE Congress on Evolutionary Computation. Trondheim, Norway: IEEE, 2009: 415−422.

[13] LI Changhe, YANG Shengxiang. A general framework of multipopulation methods with clustering in undetectable dynamic environments[J]. IEEE Transactions on Evolutionary Computation, 2012, 16(4): 556−577.

[14] Brest J, Korošec P, Šilc J, et al. Differential evolution and differential ant-stigmergy on dynamic optimisation problems[J]. International Journal of Systems Science, 2013, 44(4): 663−679.

[15] LIU Lili, YANG Shengxiang, WANG Dingwei. Particle swarm optimization with composite particles in dynamic environments[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2010, 40(6): 1634−1648.

(编辑 罗金花)

Improved multi-population gravitational search algorithm for dynamic optimization problems

BI Xiaojun1, DIAO Pengfei1, WANG Yanjiao2, XIAO Jing3

(1. College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China;2. College of Information Engineering, Northeast Dianli University, Jilin 132012, China;3. Department of Information Engineering, Liaoning Provincial College of Communications, Shenyang 110122, China)

To improve the redundant computing and low accuracy of solving dynamic optimization problems (DOPs) for multi-population algorithm, a novel improved multi-population gravitational search algorithm (IMGSA) was proposed. In IMGSA, the multi-population serial strategy was good for the present subpopulation to use evolutionary information of convergence population. A constraint initialization strategy was proposed to reduce the redundant computing which was generated by multiple populations searching repeatedly. Simultaneously, a distance decision strategy was used to stop multiple populations searching. Eventually, a monitoring and tracking strategy was used to monitor the environmental change and track the local peaks. The results show that IMGSA has a better performance in solving DOPs than those of other seven dynamic algorithms in different degree of environmental change or different peak number. It can prove the validity of proposed algorithm.

gravitational search algorithm (GSA); dynamic optimization problems (DOPs); multi-population strategy

10.11817/j.issn.1672-7207.2015.09.023

TP18

A

1672−7207(2015)09−3325−07

2014−09−26；

2014−11−30

国家自然科学基金资助项目(61175126)；中央高校基本科研业务费专项资金资助项目(HEUCFZ1209)；高等学校博士学科点专项科研基金项目资助课题(20112304110009)；黑龙江省博士后基金资助项目(LBH-Z12073)；辽宁省教育厅科学研究一般项目(L2012458)；辽宁省博士科研启动基金资助项目(20120511) (Project(61175126) supported the National Natural Science Foundation of China; Project(HEUCFZ1209) supported by the Fundamental Research Funds for the Central Universities; Project(20112304110009) supported by the Special Scientific Research Foundation of the Doctoral Program of Higher Education; Project(LBH-Z12073) supported by Post Doctoral Fund of Heilongjiang Province; Project(L2012458) supported by General Project of Scientific Research of the Education Department of Liaoning Province; Project(20120511) supported by the Doctoral Research of Liaoning Province)

毕晓君，博士，教授，从事信息智能处理技术、智能优化算法、数字图像处理研究；E-mail: 398317196@qq.com