PEX250×1000型细碎复摆颚式破碎机主要机构的优化设计

□ 乔国栋 □ 胡俊波 □ 赵 杰

1.东华理工大学 江西省新能源工艺与装备工程技术研究中心 南昌 330013 2.新建县大塘坪乡 村镇规划建设环境保护管理所 南昌 330019

PEX250×1000型细碎复摆颚式破碎机主要机构的优化设计

□ 乔国栋1□ 胡俊波2□ 赵 杰1

1.东华理工大学 江西省新能源工艺与装备工程技术研究中心 南昌 330013 2.新建县大塘坪乡 村镇规划建设环境保护管理所 南昌 330019

以PEX250×1000细碎复摆颚式破碎机为研究对象，根据“多碎少磨”的理念，把综合指标作为目标函数，调用MATLAB优化工具箱中的算法，在合理设定的约束条件下，求解得到颚式破碎机机构优化后的参数，优化后机构的运动特性较优化前有较大改善，并在同等电能功耗情况下，破碎生产率得到显著提高。

复摆颚式破碎机 综合指标 机构优化 尺寸参数

复摆颚式破碎机是矿山、冶金、建筑等行业中用于各种矿石破碎加工的设备，在我国广泛被应用于矿石粗碎领域，而在矿石中碎和细碎加工阶段应用较少。破碎机机构尺寸参数的设计是决定该产品性能优劣的关键，如何节能、高效地完成破碎过程是当前破碎机发展的目标和方向。传统的复摆颚式破碎机，具有故障率低、耐磨部件损耗小、堵塞情况少的优点，但是其破碎比较小，加工矿石粒度较差，生产率低。针对这一情况，采用多碎少磨的设计理念，在原有中型颚式破碎机的基础上进行优化设计，调用MATLAB优化工具箱中的算法，建立以综合性能指标为目标函数的数学优化模型，并对破碎机主要运动机构参数进行合理约束，通过计算得到最优化的运动机构参数，以降低破碎机功耗，提高破碎效率。

1 优化模型的创建

破碎机的经济技术指标是指同等功耗情况下，破碎机的生产率最高。经济技术指标主要由破碎比i、质量系数KI、综合指标Kt三个因素决定，通过分析三者之间的关系，设计合理的颚式破碎机结构参数，可提高破碎机产量，同时增加的消耗功率不是很多。

破碎比i是物料破碎前平均粒度D与物料破碎后平均粒度d之比：

通常情况下，质量系数K1表示破碎机每小时生产率Q与破碎比i的乘积：

综合指标Kt，表示破碎机质量系数K1与电动机功耗N之比：

1.1 复摆颚式破碎机结构简介

将复摆颚式破碎机简化为一个平面四杆机构，如图1所示。图中偏心轴的偏心距、动颚轴承中心至动颚肘板衬垫中心距、肘板长度、偏心轴固定支座中心至肘板固定支承点距离，分别对应于四杆机构的曲柄、连杆、摇杆和机架。以曲柄中心点A为原点，作XAY坐标系（水平方向为Y轴，竖直方向为X轴），图示各杆AB、BC、CD、AD、BN、C1M的长度分别为 r、L、R、f、L1、L2。

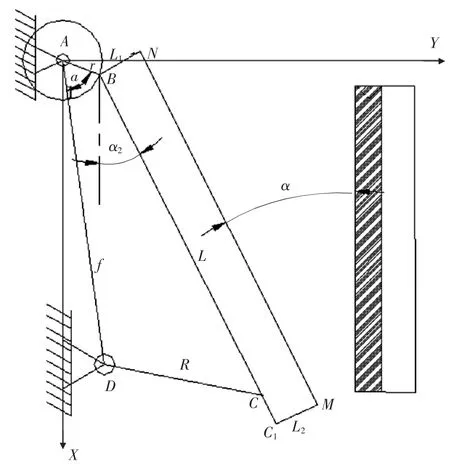
▲图1 复摆颚式破碎机机构运动简图

1.2 设计变量的确定

破碎机机构尺寸参数是指由机构简化所得的平面四杆机构的各杆长度、机架位置及连杆上动点位置等，为此选取偏心距r、肘板长度R、动颚连杆长度L、机架长度f、啮角α 5个参数为设计变量，并令：

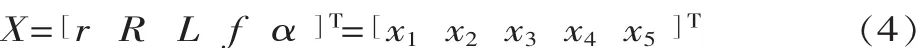
2 目标函数的建立

在机构优化设计中，取式（3）最佳综合指标为目标函数，破碎机每小时生产率的理论计算为：

式中：n为偏心轴转速；s为动颚下端水平行程；d为排料口宽度；酌为破碎物料密度；K为破碎物料松散系数。

破碎机需用功率：

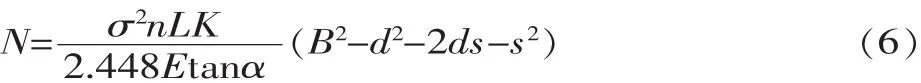
破碎机公称破碎比：

将式（3）、式（5）、式（6）代入式（7），得到目标函数综合指标：

式中：E为物料的纵向弹性模数；滓为物料抗压强度极限；B为物料的宽度，选定B=0.25 m；s为动颚下端水平行程；d为排料口宽度，d=1.5 cm。

设计该破碎机主要应用于中硬度石灰石，通过查阅相关资料得到中硬度石灰石E=0.042 MPa、酌=1.6 t/ m3、滓=123 MPa。

如图2所示，根据三角形正余弦定理得到动颚连杆L、偏心距r、肘板长度R、机架长度f、啮角α、肘板角茁、肘板摆动角渍之间的关系式：

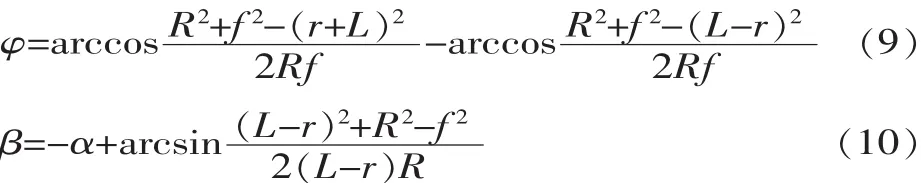
图2所示的动颚下端水平行程s：

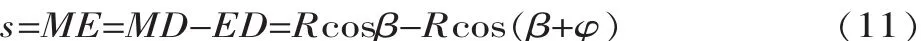
将式（7）~式（9）代入式（6），得到目标函数：

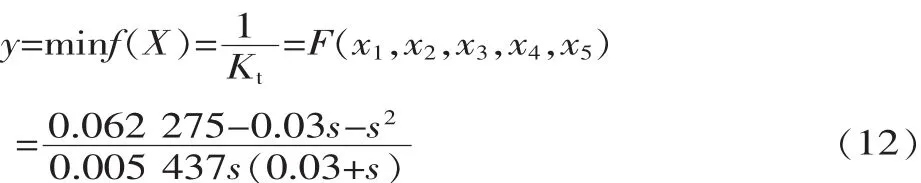
3 优化设计

3.1 约束条件的设定

3.1.1 边界约束条件

通过查阅相关文献资料，啮角α取18°≤琢≤22°，机架长度f取0.6 m≤f≤0.8 m，动颚连杆L取0.8 m≤L≤0.9 m，肘板长度R取0.3 m≤R≤0.4 m，偏心距r取0.005 m≤r≤0.009 m。

3.1.2 四杆机构曲

柄存在条件与杆长条件

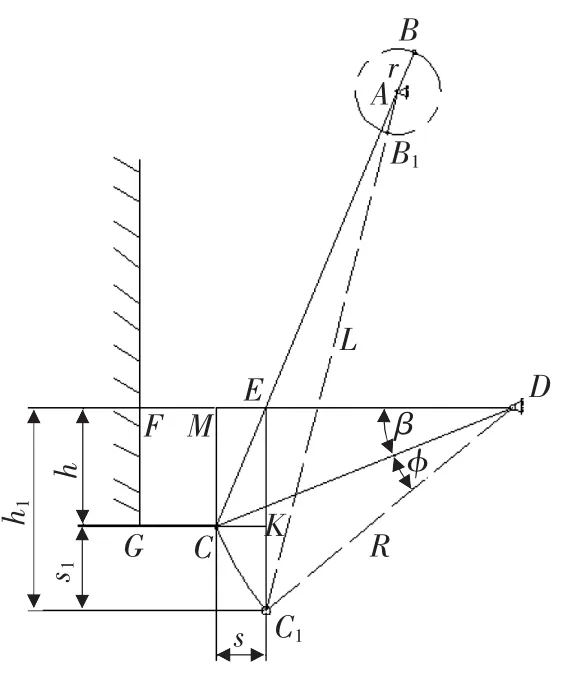
▲图2 计算示意图

复摆颚式破碎机的简化机构是一个曲柄摇杆机构，根据四杆机构曲柄存在的条件，四杆长度应满足“最短杆与最长杆长度之和小于或等于其余两杆长度之和，曲柄为最短杆”的要求。

3.1.3 传动角约束条件

肘板传动角是指四杆机构中连杆动颚轴线与摇杆肘板轴线之间所夹的锐角。传动角取45~55°，传力性能好，传动效率高，同时增加动颚下端的垂直行程，降低水平行程，从而减小齿板的磨损，减小功耗。

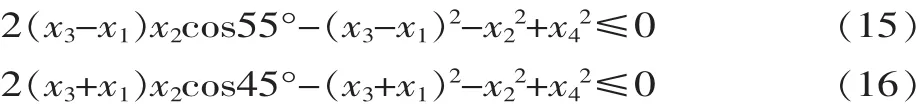
3.1.4 肘板摆角约束条件

肘板摆角渍=3~6°，肘板角茁=16~28°，减小了肘板的尺寸，并可避免机构运动时肘板发生滑动。

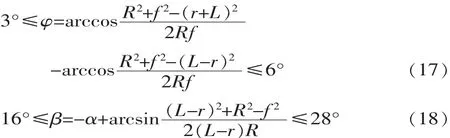
3.1.5 排料口水平行程约束条件

在设计粗碎或中破碎机时，动颚在排料口的水平行程由式（19）求得，但取值会低，所以常用经验公式（见式（20）），s取7~15 mm，式中B为进料口宽度，bmin为最小排料口宽度即图2中GC距离。

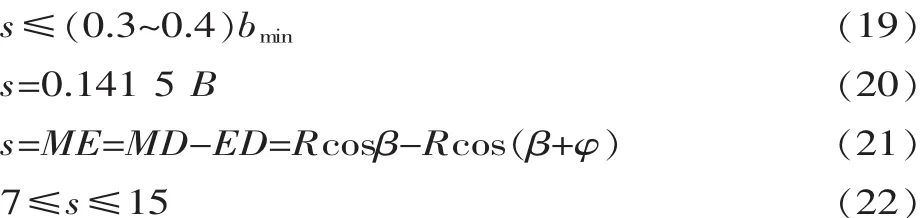
将式（17）、式（18）代入式（21），得到：

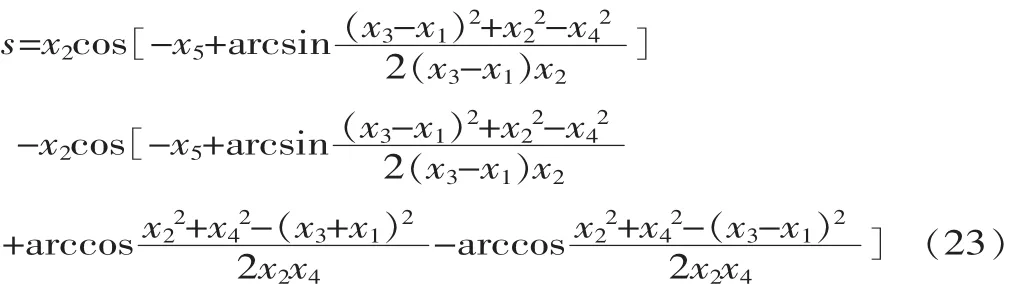
3.2 优化方法及结果

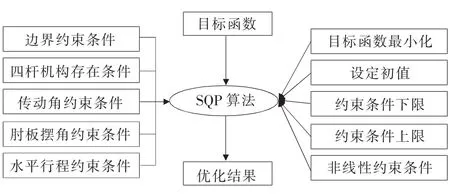
▲图3 优化方法流程图

破碎机结构的优化模型属于非线性约束的最优化问题,图3为优化方法流程图，其中采用序列二次规划法SQP算法，用来求解不等式约束的非线性规划问题。使用MATLAB优化工具箱中的fmincon函数,通过设定各参数变量初值，并对各参数约束条件上下限进行设定，再采用式（12）中求目标函数的最小值方法，最后对各参数物理意义进行非线性约束条件设定，其机构参数优化结果见表1。

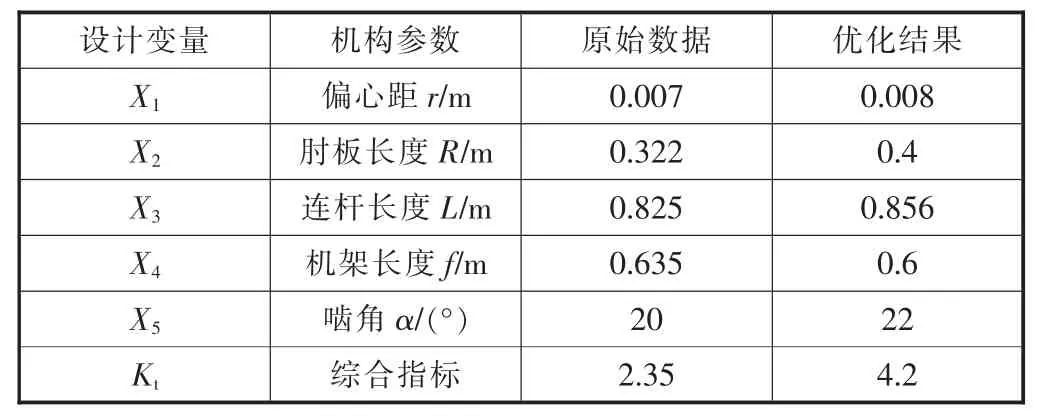
表1 机构尺寸参数优化计算结果

4 结论

对机构尺寸参数的优化结果显示，偏心距由0.007 m增大到0.008 m，肘板长度0.322 m增大到0.4 m，动颚长度由0.825 m增加到0.856 m，机架长度由0.635 m减小到0.6 m，啮角由20°增加到22°，综合指标由2.35增加到4.2，机构的运动特性得到改善，同时在同等电能功耗情况下，破碎生产率得到显著提高。

［1］ 戴少生.复摆细碎颚式破碎机偏心轴的转速计算［J］.矿山机械，1991（2）：7-10.

［2］ 戴少生，王旦容.复摆型颚式破碎机的功率计算一、二［J］.水泥工程，2001（5-6）.

［3］ 戴少生，王旦容，臧人立，等.S-p型倒悬挂细碎颚式破碎机的综合优化设计［J］.矿山机械，2002（7）：17-21.

［4］ 戴少生.新型细碎颚式破碎机的研制［J］.上海建材学院学报，1991,4（1）：29-36.

［5］ 黄大明,蒋顺梅,杨春兰.基于最小特性值的破碎机机构参数Matlab优化设计［J］.机械设计与制造，2012（1）：4-6.

［6］ 黄大明,蒋顺梅,李兆军.基于最小特性值的破碎机机构参数优化设计［J］.广西大学学报，2011,36（2）：222-227.

［7］ 卢利新.颚式破碎机的优化［J］.天津冶金，2009（3）：21-23.

（编辑 小 前）

TH123；TD 451+.2

A

1000－4998穴2015雪07－0031－03

2015年1月