变载荷作用下柔顺关节变宽度片弹簧的变形分析
□ 王 芳 □ 章 军,2 □ 刘光元
1.江南大学 机械工程学院 江苏无锡 214122 2.江苏省食品先进制造装备重点实验室 江苏无锡 214122
变载荷作用下柔顺关节变宽度片弹簧的变形分析
□ 王 芳1□ 章 军1,2□ 刘光元1
1.江南大学 机械工程学院 江苏无锡 214122 2.江苏省食品先进制造装备重点实验室 江苏无锡 214122
提出一种以变宽度片弹簧为骨架的气动柔顺关节,可构成柔性自适应机械手。片弹簧的变形等效于弹性悬臂梁自由端受特殊变载荷作用的大扰度变形。采用分段非线性变系数并带有未知参数的微分方程建立静态模型,借助MATLAB中的BVP4C函数得到不同压力下片弹簧任意位置的变形倾角、变形位移的数值解,变载荷明确后利用ANSYS建模仿真,验证结果的正确性。与等宽度片弹簧对比后说明,变宽度片弹簧骨架关节具有柔性好、节省能源的优点。
变宽度片弹簧 悬臂梁 特殊变载荷 大扰度变形 柔顺关节
传统工业机械手只能抓持形状大小相同、位置状态一致、不会破损的刚性工件,而仿人灵巧机械手需要精确感知复杂对象,然后控制运动和抓持力,因此结构复杂、价格昂贵,目前尚处于实验室研究阶段。针对以上情况,本文提出一种变截面片弹簧柔顺关节,该关节有着较好的柔顺型与适应性,可以满足抓持大小不一、形状各异、易伤易碎物品的要求。
片弹簧变形等同于悬臂梁的大挠度变形分析[1-2],在悬臂端的作用力为特殊变载荷 (大小和方向随气缸压强的增大呈现非线性变化)。由于片弹簧变形时的载荷未知,无法用有限元软件ANSYS或Abaqus直接建模仿真求解[3-4]。研究柔顺机构方法还有伪刚体模型法[5-7],但是目前这种方法对特殊变载荷作用的悬臂梁还不能建立较为精确的模型。Banerjee等[8]利用非线性打靶和Adomian[9]分解方法以及钱伟长[10]、何晓婷[11]等采用双参数摄动法研究了大变形梁的数值解,为大变形数值求解提供了很好的思路,但是这些方法都是以悬臂梁自由端的作用力是方向不变的力为先决条件的,不适用于本文阐述的特殊变载荷状况。
1 片弹簧的静态模型与计算
1.1 静态模型
柔性关节结构如图1所示,尾座3和头座7通过螺栓8分别与指根节1和指尖节9连接,尾座与指根节、头座与指尖节中间均夹有调节垫片2,两端的偏心距可以根据需要调节。笔型气缸5为双耳环笔型气缸,双耳环连接件6通过销与单耳环支座4相连,单耳环支座分别固定在头座和尾座上。片弹簧13通过螺栓固定在指尖节和指根节的凹槽内,并且由压板10压紧,由防松垫圈11和螺母12锁紧固定。指根节和指尖节中间的凹槽是为了限制片弹簧的自由度,保证片弹簧中心线和气缸轴线在同一平面内。
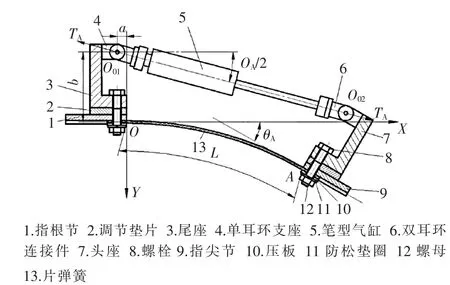
▲图1 柔顺关节结构图
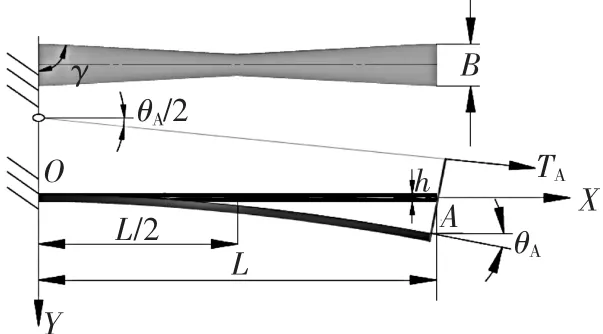
▲图2 片弹簧受力分析图
图1中,a为耳环销轴中心线到O点的水平距离,b为耳环销轴中心线到O点的竖直距离。关节结构对称,工作长度为L的片弹簧,左右两端相关零件(头座、尾座等)的轴、径向尺寸完全相同。假设片弹簧长度L变形后保持不变,忽略所有零件重力,此时片弹簧的大变形等效于特殊变载荷作用下悬臂梁的大变形,以片弹簧为主要研究对象,建立坐标系并对片弹簧进行受力分析,如图2所示。
图2中点O和点A分别为等效悬臂梁的固定端和自由端,兹A为自由端变形倾角,TA为气缸对头座的推力。由于关节结构对称,两端均为铰链安装的气缸可以简化为一个可以伸长的二力杆,无论是指根节还是指尖节作为悬臂梁的固定端 (本文以指根节固定进行分析),在相同气压下,气缸活塞的伸长量和气缸角位移必定相同,所以气缸角位移(即气缸推力与水平线夹角)和片弹簧中点处截面转角为兹A/2。在悬臂自由端A处,设头座对片弹簧的作用力和力偶分别为TAx、TAy和Me,则有:
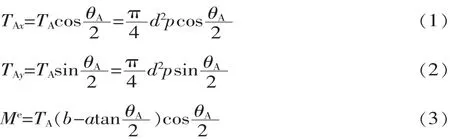
式中:d为气缸内径;p为气体压力。
梁上任一位置的弯矩M:
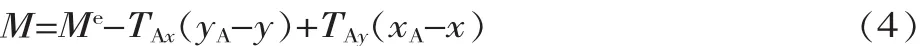
式中:xA、yA和x、y分别是自由端A变形后在X、Y轴方向的坐标。

梁上任一位置的曲率籽与该位置弯矩M之间的关系为:式中:E为弹性模量;I为主惯性矩;c为片弹簧任意位置的宽度;h为片弹簧厚度;s为弧长(即片弹簧弯曲变形时任意位置的弧长);兹为任意位置变形倾角。
将式(4)代入式(5),即有:
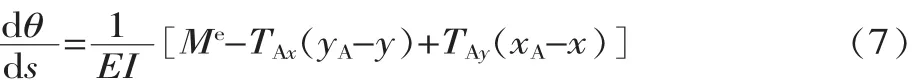
当0≤s≤L/2时,对称双梯形片弹簧任意位置宽度表示为任意位置长度的函数:
c=B-2scot酌 (8)
如图2所示,B为片弹簧最大宽度 (弹簧两端宽度),酌为片弹簧截面夹角。将式(1)、式(2)、式(3)、式(8)合并到式(7),并整理得:
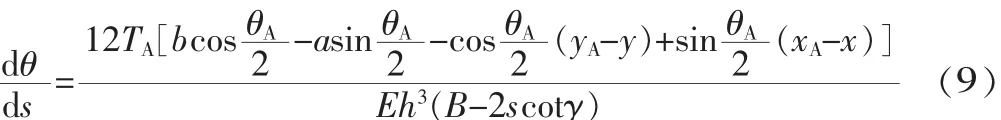
式(9)两端对弧长s求微分,由大变形分析中的精确微分关系式:

可得:
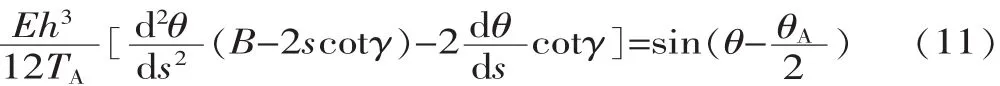
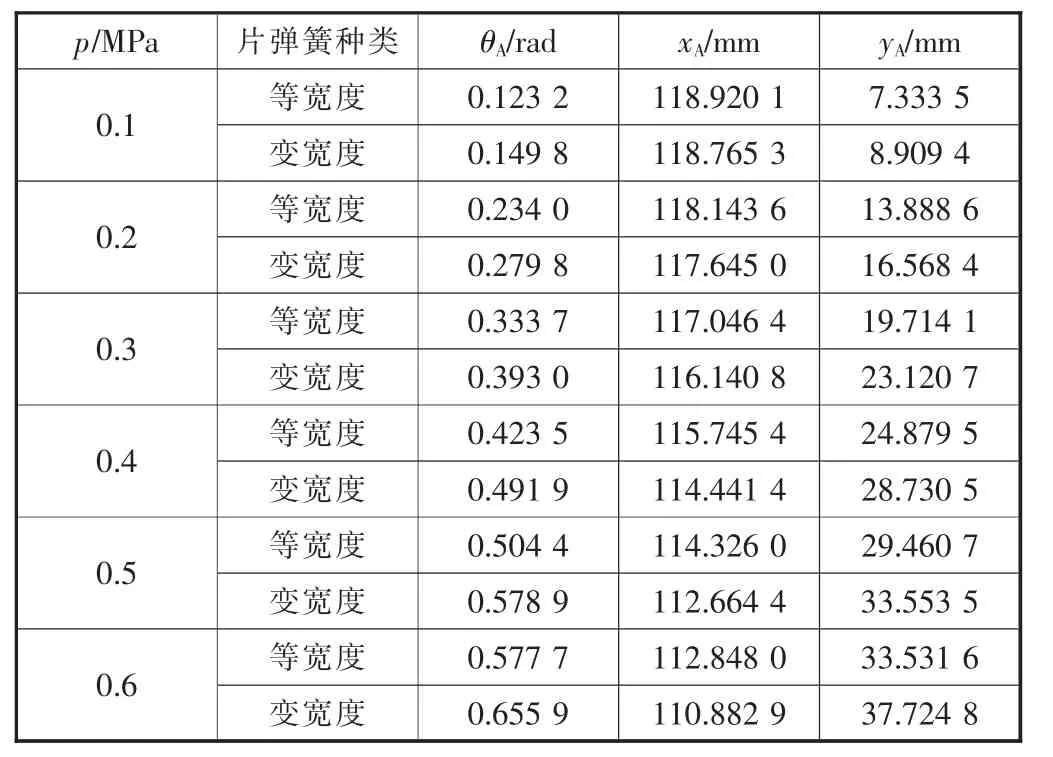
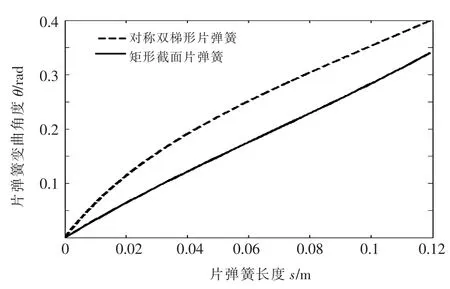
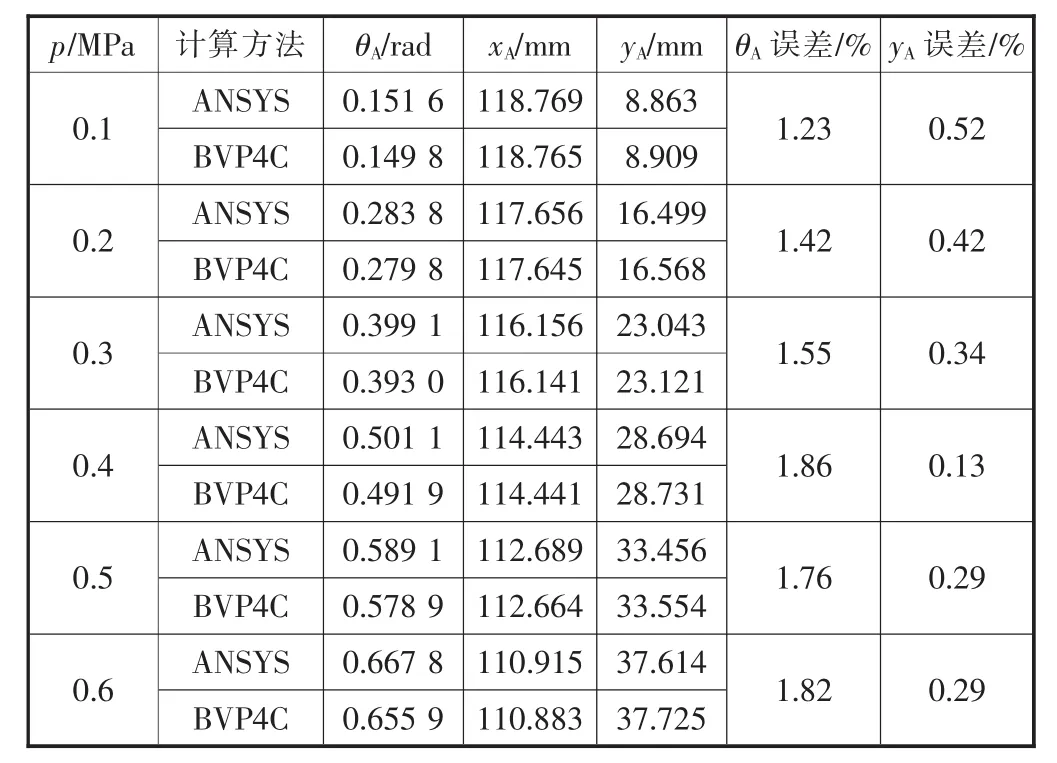
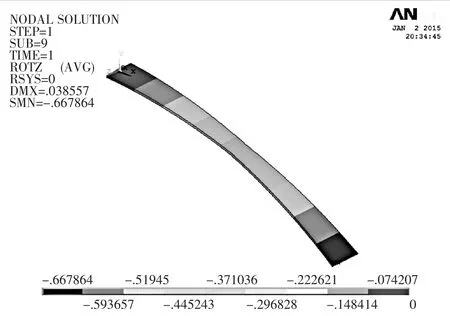
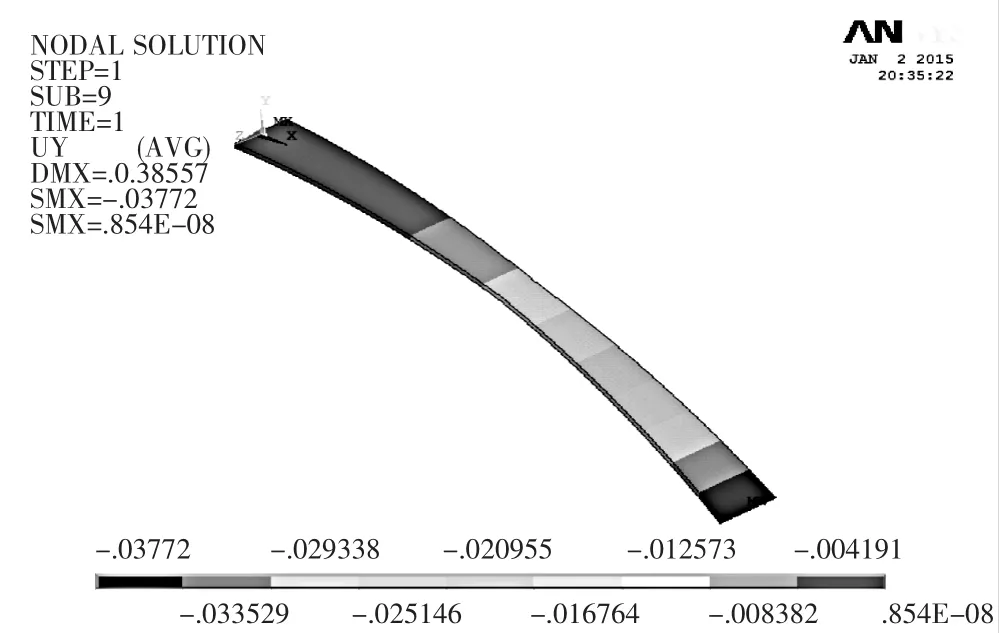
当L/2 同理,可得: 根据式(11)、式(14)可知,变形倾斜角兹是片弹簧弧长s的二阶非线性变系数常微分方程。 1.2 模型的数学计算 1.2.1 变形倾角兹A的微分计算方法 本文采用配置法[12],借助MATLAB中的BVP4C求解器,将方程的求解转化为带有未知参数的边值问题,最终得到变形倾角和坐标位移的数值解。求解边值型问题除了正确定义方程外,最重要的是选取合适的边界条件。首先将式(11)、式(14)降阶为一阶方程组,然后确定边界条件。在悬臂梁固定端,已知当s=0时,x=0,y=0,又因为当s=L/2时,兹=兹A/2即片弹簧关于中点横截面成对称弯曲,根据对称弯曲可以得到关系式tan兹A=yA/xA,将上述关系代入式(9),得到边界条件: 在悬臂梁自由端,已知当s=L时,x=xA,y=yA,将该关系式代入式(13),得到边界条件: 将边界条件式(15)、式(16)代入式(11)、式(14)中,把兹A看成未知参数,任意给定未知参数初值,循环求解,即可得到片弹簧上任意位置变形倾角的数值解。 1.2.2 位移变形坐标微分计算方法 在兹求出之后,兹A已知,代入到式(11)、式(14)中并分别联立式(10)得到方程组: 定义好方程组之后,选取前半段合适的边界条件。已知边界条件: 将式(17)作降阶处理然后代入边界条件式(19),即可得到片弹簧前半段任意位置的变形坐标位移数值解,这时片弹簧中点位置坐标(xM,yM)已知,所以得到后半段的边界条件: 同理,将式 (18)作降阶处理后代入边界条件式(20),即可得到片弹簧后半段任意位置的变形坐标位移数值解。至此,片弹簧上任意位置的变形倾角和变形坐标位移都已得到求解,接下来将通过在ANSYS中建模仿真和实物测量两种方式来验证数值微分方法的正确性。 在实验验证中,经过测量变宽度片弹簧骨架柔性关节的结构尺寸:气缸直径d=10 mm,行程为30 mm,初始状态气缸未伸出时其连接销中心的距离S0= 125.72 mm。选用60Si2MnA弹簧钢做成对称双梯形截面的片弹簧,宽B=11.90 mm,厚度h=1.04 mm,工作长度L=119.22 mm,梯形截面夹角γ=88°,弹性模量约为E=190 GPa,a=3.25 mm,b=29.35 mm。为了使对比更具有说服力,选取同样尺寸的等宽度片弹簧骨架柔性关节进行数值模拟,以证明新关节的优越性。 在给定的压力p下,对式(11)、式(14)、式(17)、式(18)求解,得出p=0.1 MPa、p=0.2 MPa、p=0.3 MPa、p= 0.4 MPa、p=0.5 MPa、p=0.6 MPa时,变宽度片弹簧任意位置变形倾角和坐标位移的数值解,再与等宽度片弹簧变形参数作对比,对比曲线如图3所示,由于趋势相同仅数值不同,因此只给出p=0.3 MPa的曲线。列出自由端A点的详细数值,见表1。 表1 两种片弹簧的压力p与A点数值计算 ▲图3 p=0.3 MPa时变形倾角随弧长的变化曲线 在相同的压强下,由表1可知,变宽度片弹簧较之于等宽度片弹簧具有更大的弯曲变形角。从图4可以看出,在相同的压强下,变宽度片弹簧与等宽度片弹簧相比,变形角的变化率更大,即相同长度的弧长间隔,前者的变形倾角变化更大。说明对称双梯形片弹簧相比于等宽度片弹簧有着较好的弯曲性能,使得以变宽度片弹簧骨架柔性关节组成的机械手比由等宽度片弹簧骨架柔性关节组成的机械手有着更大的抓持范围和更节省能源的优点。 本文中片弹簧自由端由于所受的载荷与变形倾角耦合在一起,无法建立一一对应的力与变形的关系,所以无法直接在ANSYS中建模计算。本文先采用数值微分法计算出不同压强下片弹簧的变形,进而确定出变载荷的大小与方向,然后加载到ANSYS模型中,最后与理论计算值对比,分析误差来验证数值微分法的正确性。图4和图5分别给出p=0.6 MPa加载后的变形倾角和纵坐标位移云图,表2列出A点变形参数数值并与理论计算值的对比。 表2 ANSYS模拟结果与理论计算数值对比表(自由端A点) ▲图4 变形倾角位移云图 ▲图5 纵坐标位移云图 由表2可知,变形倾角的误差在2%以内。由于横、纵坐标位移变化较小,这里只给出了纵坐标位移的误差值,而纵坐标位移的误差也只在0.5%左右,整体来看误差很小,这充分证明了数值解法的正确性。而且由于片弹簧产生大变形弯曲,中性面会发生偏移不再与几何中心面重合,这会使理论建模计算有较大的误差。本文通过数值微分法先计算变形参数,然后再加载到ANSYS中,不仅可以验证变形参数,还可以得到应力的分布状况和详细数值,为变载荷作用下无法确定载荷方向与大小的悬臂梁大挠度变形问题提供一种行之有效的方法。 本文提出的柔顺关节以气缸为驱动器,对称双梯形片弹簧为柔性骨架,由于气体压缩性强和片弹簧的特点,使得该关节结构具有很好的柔性自适应性和缓冲性;相比于文献[1]的等宽度片弹簧骨架柔顺关节,新关节有着更大的抓持范围、需要较小驱动力的优点。而其中间细两端宽的形状更符合应力的分布状况,更容易弯曲变形,从而减小变形阻力,减轻关节重量,节约了能源,关节运动更灵活,动态响应性更好。 在数值解法上,采用微分方法建立模型,利用配置数值方法求解,并用ANSYS建模仿真验证,解决了特殊变载荷变截面悬臂梁的大挠度变形问题。与龙格库塔法相比,在满足精度要求的情况下,该解法具有求解速度快的优点,方便应用阶段中的实时控制。 [1] 刘光元.变载荷作用下柔性关节片弹簧的大变形分析与强度计算[J].机械科学与技术,2013,32(1):111-115. [2] Jun Zhang,Qiu J Zhang.Bending of Flexible Joint Driven by LinearExpandablfArtificialMusclf [J].International Journal of Modelling and Simulation,2011,1:1-5. [3] P F Pai,A N Palazotto.Large-deformation Analysis of Flexible Beams [J].International Journal of Solids and Structures,1996,33(9):1335-1353. [4] Jinyang Liu,Jiazhen Hong.NonlinearFormulation for Flexible Multibody System with Large Deformation[J].Acta Mechanica Sinica,2007,23(1):111-119. [5] Larry L Howell.Compliant Mechanisms[M].John Wiley& Sons,Inc,USA,2001. [6] 李海燕,张宪民,彭惠青.大变形柔顺机构的驱动特性研究[J].机械科学与技术,2004,23(9):1040-1043. [7] J J Yu,S S Bi,G G Zong.Kinematics Analysis of Full Compliant Mechanisms Using the Pseudo-rigid Body Model[J].Chinese Journal of Mechanical Engineering,2002,38: 75-78. [8] A Banerjee,B Bhattacharya,A K Mallik.Large Deflection of Cantilever Beams with Geometric Non-linearity:Analytical and Numerical Approaches[J].International Journal of Non-Linear Mechanics,2008,43(5):366-376. [9] Z F Liang,X Y Tang.Analytical Solution of Fractionally Damped Beam by Adomian Decomposition Method[J]. Applied Mathematics and Mechanics,2007,28(2):219-228. [10]Qian Weizang.Second Order Approximation Solution of Nonlinear Large Deflection Problem of Yongjiang Railway Bridge in Ningbo[J].Applied Mathematics and Mechanics, 2002,23(5):493-506. [11] XiaotingHe, Shanlin Chen.Biparametric Perturbation Solutions of Large Deflection Problem of Cantilever Beams[J].Applied Mathematics and Mechanics,2006,27(4):453-460. [12]Finlayson Bruce A.Nonlinear Analysis in Chemical Enginee鄄ring[M].New York:McGraw-Hill College,1980. (编辑 丁 罡) TH122 %% %%%% A 1000-4998穴2015雪07-0008-04 2015年1月
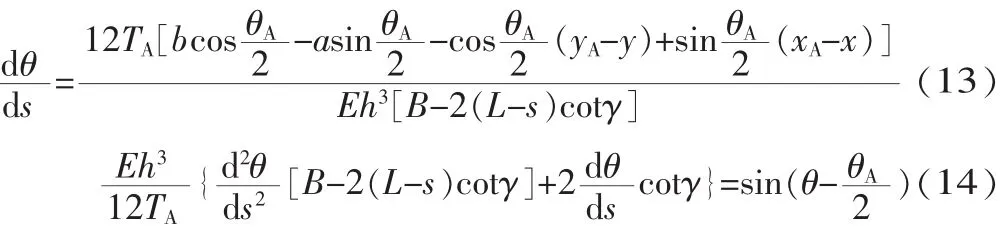
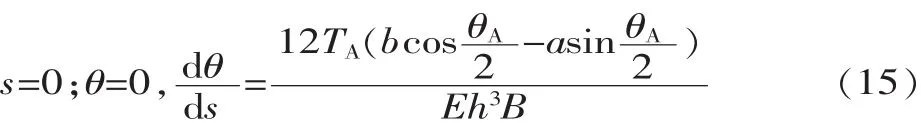
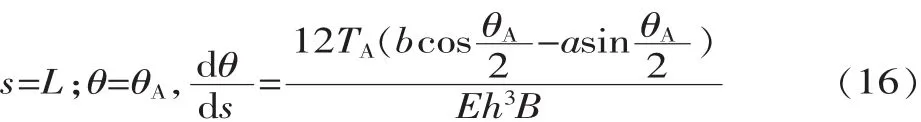
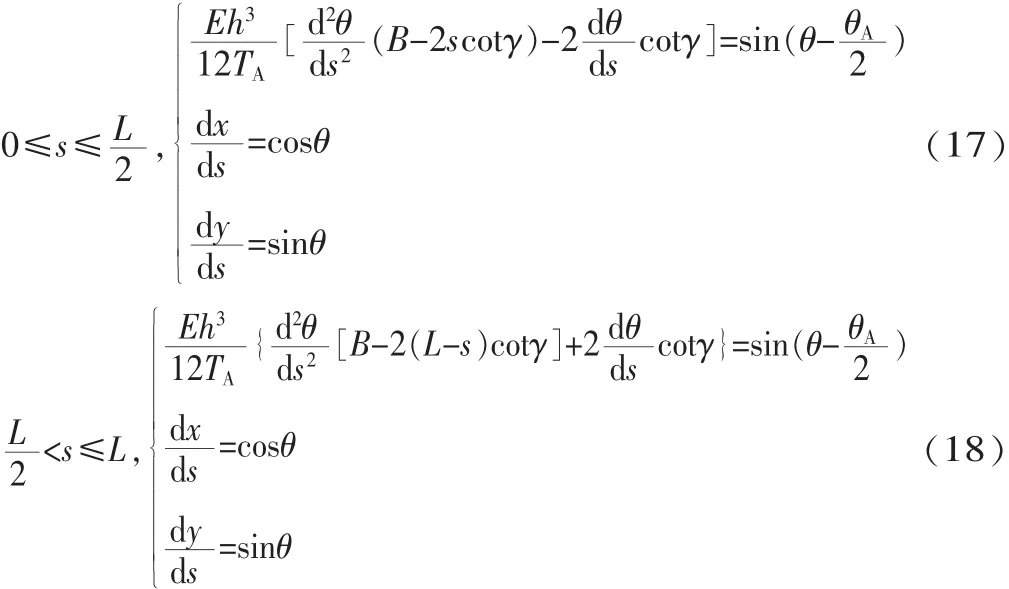

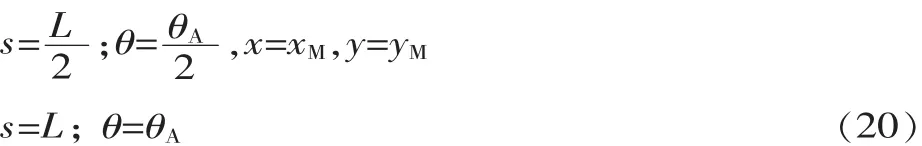
2 实例与对比
3 ANSYS仿真模拟
4 结论

