颚式破碎机机架的有限元分析及拓扑优化

刘光浩，娄玉印，莫文锋

（1.柳州职业技术学院，广西柳州545005；2.广西科技大学鹿山学院，广西柳州545005）

颚式破碎机机架的有限元分析及拓扑优化

刘光浩1，娄玉印2，莫文锋1

（1.柳州职业技术学院，广西柳州545005；2.广西科技大学鹿山学院，广西柳州545005）

基于鄂式破碎机机架重量较大，结构不合理的现状，运用有限元分析软件hyperworks建立颚式破碎机机架的有限元模型；根据颚式破碎机的力学分析对其进行有限元静强度分析；根据有限元分析结果，以颚式破碎机机架的重量最小为目标，颚式破碎机机架的最大应力为约束条件，对其进行拓扑优化设计，得出颚式破碎机机架更加合理的模型，对后续颚式破碎机机架的减重优化和对企业生产有一定的指导意义。

APDL；颚式破碎机机架；拓扑优化

国内颚式破碎机机架是颚式破碎机的重要组成部分，是鄂式破碎机其它零件安装的基础。它在工作中承受很大的冲击载荷，是破碎机的关键部件[1-2]。但目前颚式破碎机机架的设计大多都是通过类比，按经验确定各个部件的形状和尺寸。是依据传统的经验结论而不是科学的计算方法进行的，采用这种传统的设计方法，具有一定的盲目性，很难设计出既经济又满足强度和刚度要求的颚式破碎机机架[1]。

本文采用现代设计方法有限元分析方法——首先对颚式破碎机机架进行有限元静强度分析，其次以颚式破碎机机架重量最小为目标，以最大应力为约束条件，得出颚式破碎机机架的拓扑模型，该分析为颚式破碎机企业对破碎机的研究起到一定的指导作用，对降低颚式破碎机的研发周期，降低颚式破碎机的制造成本、延长颚式破碎机的使用寿命起到一定的积极作用。

1　结构介绍

如图1所示是PFE-600×900颚式破碎机的结构示意图，定颚固定在机架的前壁上，动颚通过轴承直接悬挂在偏心轴上，偏心轴由皮带轮带动旋转，动颚下端通过肘板和固定在机架的支座相连。当电机转动时带动皮带轮转动，同时偏心轴带动动颚转动；动颚一方面对定颚作往复摆动，同时还顺着定颚有很大程度的上下运动[2-3]。

图1　颚式破碎机的结构示意图

2　力学分析

颚式破碎机受力如图2所示。

图2　破碎机在最大破碎力时的机构受力示意图

列平衡方程：

∑FX＝0，即

∑FY＝0，即

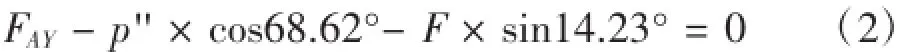
∑MA（F）＝0，即

由上式得：FAX=-138.21 kN，FAY=2 587.38 kN，F=4 224.38 kN

且FA与X轴正向的夹角是93.06°.

所以由作用力反作用力的性质知肘板对机架的作用力F'=4 224.38 kN，方向与X轴正方向的夹角为-14.23°.

2　有限元分析

鄂式破碎机机架是颚式破碎机的重要部件，对破碎机破碎性能起到重要的作用。为此运用有限元分析软件hyperworks建立颚式破碎机机架的有限元模型，对其进行有限元静强度分析。

（1）模型的建立。首先利用UG三维设计软件按照实际图纸尺寸建立破碎机机架的实体模型，再导入到hypermesh有限元分析软件，采用hypermesh中的智能划分网格方法。经智能网格划分破碎机机架的有限元模型如图3所示，节点的数目为197 893，单元数目为77 716.

图3　破碎机机架的有限元模型

（2）设定材料特性：根据结构参数，破碎机机架的材料为45号钢。该材料的弹性模量E=2.02×105MPa，泊松比μ=0.3，密度ρ＝7.85×10-6kg/mm3，屈服极限为σs=355 MPa.

（3）单元选择。基于破碎机架结构复杂，本文选用三维实体SOLID92.SOLID92单元由十个点定义，每个节点有三个自由度：节点x、y和z方向位移[4]。

（4）添加载荷、约束求解。根据前面的力学分析，加载肘板对机架的作用力F'=4 224.38 kN，方向与X轴正方向的夹角为-14.23°.将颚式破碎机机架底部设为全约束。

（5）经有限元分析后计算得破碎机机架的应力云图，如图4所示。可知，破碎机机架的应力大部分集中为53 MPa，远小于许用应力；最大应力为480 MPa，发生在机架安装肘板应力集中处，满足强度条件。破碎机机架的变形云图，如图5所示，坑机机架的最大变形为0.43 mm，发生在安装轴承处，满足刚度条件。

图4　破碎机机架的受力云图

图5　破碎机机架的变形云图

3　颚式破碎机机架的拓扑优化

为了得到更合理的机架结构，对此结构进行了拓扑优化。将颚式破碎机机架（如图6所示）设为不变区，其余部分设为拓扑区域[5-6]，将机架体积最小设为优化目标[7]，设最大应力小于53 MPa，基于此利用HyperMesh进行拓扑优化。得到的结果如图7所示。

图6　破碎机机架的拓扑模型

图7　颚式破碎机机架有限元分析拓扑结果

如图7所示，破碎机机架左右两侧和左侧应力较小，为后续设计优化的主要区域，对企业颚式破碎机机架的设计有一定的帮助作用。

4　颚式破碎机机架再设计

（1）根据上面破碎机机架的拓扑优化结果，对破碎机的左右和前后机构进行再设计，运行三维建模软件UG再次建模如图8所示。

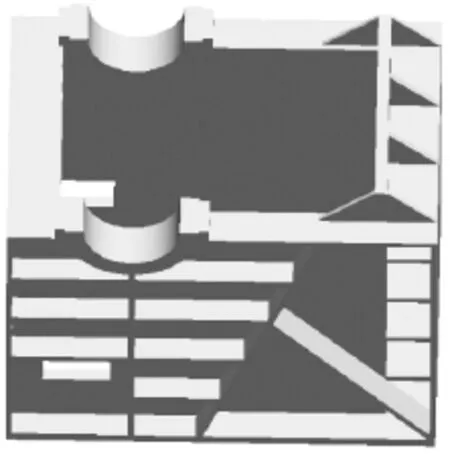
图8　颚式破碎机机架二次设计

（2）有限元分析

经有限元分析后计算得破碎机机架二次设计的应力云图，如图9所示。可知，破碎机机架的应力大部分集中为53 MPa，远小于许用应力；最大应力为2 419 MPa，发生在机架安装固定位置，该位置为应力集中位置，可不考虑。破碎机机架的二次设计的变形云图，如图10所示，破碎机机架的最大变形为1.9 mm，发生在安装轴承处，满足刚度条件。

图9　破碎机机架二次设计的受力云图

图10　破碎机机架的二次设计变形云图

经再次设计后破碎机机架强度和刚度都能得到很好的满足，重量由原来0.77 t变为0.70 t，重量减少了10%，起到了减重优化的结果。

5　结束语

（1）通过有限元分析可知再次设计后的颚式破碎机机架满足强度和刚度要求，且重量有所减轻，起到了减重优化的结果。

（2）通过结构拓扑优化，得到颚式破碎机机架的拓扑模型，对后续企业破碎机的生产有一定的指导意义。

（3）在破碎机机架设计过程中，引入拓扑优化设计方法，能极大地提高颚式破碎机的精度和质量，保证材料的最大利用率，从而降低生产成本，并且提高产品的性能。

[1]任红英，张岐生.颚式破碎机优化设计与实践[J].萍乡高等专科学校学报，2001，12（4）：28-32

[2]黄冬明.挤压类破碎机工作机理和工作性能优化研究[D].上海：上海交通大学，2009

[3]卢利新.颚式破碎机的优化[J].天津冶金，2009，6（3）：21-23.

[4]S.Nikolove.Modelling and Simulation of Particle Breakage in Impact crushers[J].International Journal Mineral Process， 2004，（74）：219-225.

[5]A.Thomas.L.O.Filippoy.Fractals and Breakage Energy of Mineral Particles[J].International Journal Mineral Process，1999，（57）：285-301.

[6]王钰栋，金磊，洪清泉.HyperMesh&HyperView应用技巧与高级实例[M].北京：机械工业出版社，2012：150-151.

[7]于开平，周传月，谭惠丰.HyperMesh从入门到精通[M].北京：科学出版社，2005：250-251.

Finite Element Analysis and Topology Optimization of the Frame of Jaw Crusher

LIU Guang-hao1，LOU Yu-yin2，MO Wen-feng1
（1.Liuzhou Vocational&Technical College，Liuzhou Guangxi 545005，China；2.Lushan College of Guangxi University of Science and Technology，Liuzhou Guangxi 545005，China）

Based on the large weight of the frame of the jaw crusher，the structure is not reasonable.Firstly，the finite element model of the jaw crusher frame was established by hypermesh，and then the finite element analysis was carried out according to the mechanical analysis of the jaw crusher.With a jaw type crushing machine frame of the minimum weight as the goal，jaw broken machine frame of the maximum stress as constraint conditions，the topology optimization design，draw the jaw crusher machine more reasonable model，on subsequent jaw type crushing machine weight optimization of the and of the production enterprises have certain guiding significance.

APDL；jaw crusher frame；topology optimization

TD451

A

1672-545X（2016）10-0018-03

2016-07-03

项目编号：桂教科研2011（14）201106LX753

刘光浩（1976-），男，湖南邵阳人，硕士，副教授，研究方向：可靠性优化设计；娄玉印（1983-），男，山东聊城人，硕士，助教，研究方向：可靠性优化设计。