一种并联分布式微源的无功功率均分控制策略

刘尧，韩华，粟梅，孙尧，谌慧滨，龙熹



一种并联分布式微源的无功功率均分控制策略

刘尧，韩华，粟梅，孙尧，谌慧滨，龙熹

(中南大学 信息科学与工程学院，湖南 长沙，410083)

在微电网多逆变器并联系统中，由于各逆变器之间的输出阻抗和馈线阻抗存在差异，因此，应用传统的下垂控制策略会导致逆变器间无功均分精度较低而造成环流问题。为了减小环流、提高无功分配的精度，提出一种改进型下垂控制的微电网无功均分策略。该方案利用低带宽通信获取各微源的无功功率信息，修改无功电压下垂特性曲线的电压偏置，达到提高无功出力分配精度的目的。同时，所提出的环流和负荷电压偏差为优化指标的目标函数，优化并设计控制参数。研究结果表明：改进的无功均分方法在不影响有功功率均分的条件下，极大提高了微源无功功率均分的精度，并具有良好的动态和稳态性能。

微电网；改进下垂控制；无功出力分配；低带宽通信技术；参数优化

分布式发电(DG)具有污染少、能源利用率高、安装地点灵活、输配电资源和输电线路损耗小等特点，逐渐成为未来大型电网的有力补充和有效支撑，是未来电力系统的发展趋势之一[1]。微电网作为分布式电源的有效载体，包含各种形式的微源、储能装置、能量转换装置、保护以及负荷控制[2]等设备，可以运行在孤岛和并网2种模式下，是近年来分布式能源接入的有效途径。在微电网中，微源逆变器并联运行控制策略一般采用基于有互联线的主从控制法[3]、集中控制法[4]及平均负载分配法[5]和基于无互联线的下垂控制[6−7]等方法。其中基于有互联线通信的方法可以达到很好的均流效果，并减少输出电压总谐波畸变率。然而，互联线的存在会限制系统的灵活性和冗余性，从而降低微电网系统的可靠性。基于无互联线的对等控制方法是源于同步电机中的下垂控制思想，利用有功功率、无功功率和电压的频率、幅值之间的对应关系来调节逆变器出电压参考值。在微电网中，由于各微源到负荷的阻抗不等，造成各逆变器的无功功率不能均分，甚至导致DG间产生严重的无功环流[8]。为解决此问题，许多研究者对传统的下垂法进行了改进。在线路阻感比很高的情况下，Engler等[9]采用反下垂特性控制逆变器输出电压的幅值和频率。当线路阻抗中的阻性成分和感性成分均不可忽略时，Brabandere等[10]采用有功功率和无功功率解耦的方法精确地控制系统输出功率，但这种方法需要精确地获得线路中阻感比。另外，文献[11]引入一种虚拟电感来防止谐波分布不均对逆变器的影响，但虚拟电抗的增加导致输出电压跌落，降低了系统电压质量，且所提出的虚拟阻抗算法对逆变器的控制带宽要求较高，实现难度较大。近年来，一些研究人员采用复合方法控制逆变器并联，在保留无互联线下垂控制特性的基础上加入通讯线[12]。张纯江等[12−13]提出了互动跟踪式无主从控制方法，通过同步BUS母线和CAN总线控制各逆变器基准信号的同步和幅值的调节实现功率均分，但通讯带宽要求和成本较高。综上所述，采用有互联线的控制方法获得了良好的并联特性但牺牲系统冗余度和增加复杂连线，采用无互联信号线的并联控制方法实现了系统冗余度，但电流均分效果下降。本文作者综合这些方法的优劣，提出一种改进下垂控制的微电网无功均分策略。该方法利用低带宽通信获取各微源的无功功率信息，用于修改无功电压下垂控制的电压偏置，提高无功出力分配精度。与传统的下垂控制策略相比，该方案具有简单且容易实现、对通信带宽要求不高和精确的无功功率均分等优点。最后，在建立2台单相逆变器并联系统的小信号数学模型[14]的基础上，通过状态矩阵特征根的分布，分析系统的动态特性，并证明系统的稳定性。

1 微电网功率下垂法基本原理

1.1 微电网的结构

微电网由分布式电源(DG)和负荷构成，每个DG单元通过电力电子接口和相应馈线接至公共母线上,其结构如图1所示。微电网可以运行在并网模式下，也可孤岛自治运行。在并网模式下，只需控制微源表现为电流源行为，因此，控制相对简单。而在孤岛模式下，需要控制微源表现为电压源以提供电压支撑，若控制稍不当，则造成无功环流问题。因此，本文仅针对孤岛模式下微电网的基波有功和无功的均分问题，提出一种改进的下垂控制算法，不考虑非线性负载均分问题。

图1 微电网的结构

1.2 传统的下垂控制

图2所示为仅含有2个分布式电源的并联系统简化原理图。在孤岛运行模式下，2个分布式单元根据自身频率和电压幅值调整输出有功和无功，保持微电网的稳定运行。

图2 2台逆变器并联系统简化原理图

由图2可得逆变器输出的有功功率P和无功功率Q为：

其中：x为逆变电源输出感抗和线路感抗之和；r为逆变电源的输出电阻和线路电阻之和；E为逆变电源输出电压幅值；δ为并联系统输出电压矢量之间的夹角；为第个分布式微源(=1，2)。

由于实际中相角偏差δ很小，可认为sinδ=δ，cosδ=1。同时，考虑实际中分布式微源通常配置串联虚拟电抗来保证系统的稳定性和满足应用下垂控制的条件[6, 11]，因此，可认为x＞＞r条件成立。于是，式(1)和(2)可分别写为：

从式(3)和(4)可以看出：各DG单元输出的有功功率P可以通过相角δ调节，无功功率Q可以通过电压幅值调节。因此，在并联逆变器无互联线通信时可以采用传统的下垂控制：

式中：*和*分别为DG在空载下输出电压的角频率和幅值；ω和E分别为DG实际输出电压的角频率和幅值；m和q分别为频率和电压的下垂增益。

将式(5)中无功表达式代入式(4)，得到无功功率的表达式：

由式(6)可知：由于实际分布式微源输出侧虚拟电抗的配置和变压器电感参数存在，故可忽略线路电 阻[6,11]。各分布式微源发出的无功功率与线路电抗x、空载电压幅值*、公共母线电压和无功下垂增益q有关。式(6)中，由于x＜＜，x＜＜*，因此，从式(6)敏感性分析可知，线路阻抗是引起分布式微源输出无功不能均分的最敏感性因素。不妨假设2台分布式微源的容量相等，则无功下垂增益设置相同。若存在不匹配的馈线阻抗1＞2，则DG1输出的无功功率小于DG2输出无功功率；而当线路参数严重不匹配时，甚至引起系统的稳定性[11]。因此，有必要对传统下垂控制进行改进。

2 改进型无功下垂控制策略及参数优化

2.1 改进型无功下垂策略的提出

由于频率为全局变量，使有功功率输出不受等效阻抗的影响，因而可以实现比例精确均分。而无功功率的偏差由线路阻抗差异、输出电压幅值差异、微电网复杂结构等因素引起。

为克服传统无功功率下垂的缺陷，提出改进型无功电压下垂控制表达式，如式(7)所示。式中：m和q分别为第台微源的频率和电压的下垂增益(=1，2，3，…)，可根据其自身容量设置；Q*为每个微源稳态时理论上输出的无功功率；K为积分时间常数；K为微分时间常数。图3所示为改进型下垂控制框图。

图3 改进型无功电压下垂控制框图

2.2 改进算法的过程和通信要求

传统的下垂控制仅采用本地无功功率，无需通信环节。本文提出的改进型无功算法在中央控制器[14]的作用下，采样微电网内各个微源的无功信息，经过无功参考计算得到平均输出功率Q*，然后将Q*通过低带宽通信分配至每个微源。微源通过式(7)中的无功功率−电压下垂表达式调整自身输出无功功率，稳态时均等于其自身参考值。从式(7)可知，本文方法采样和传统的是微源无功值(直流信号)，对通信的带宽和成本要求较低，而且微电网本身对无功分配的动态要求并不高，因此，在实际中可通过廉价的RS232/485通信实现数据传输。但需要说明的是：低带宽通信仅是实现本算法式(7)的一种通信手段，具体通信细节不是本文研究的重点。

表1所示为各算法的通信要求的比较。其中，传统的下垂控制策略无互联线通信，降低通信成本，但不能均分无功功率，从而引起系统环流。文献[12−13]采用CAN总线技术通信，需要高同步脉冲保证指令信号的一致性，因此，其带宽和通信成本较高。本文采用廉价的RS232/485通信，仅用到无功功率信息，为直流信号，其带宽和成本较低，且提高了无功功率均分的精度。

表1 各算法的通信要求比较

2.3 改进算法的参数优化

改进型无功下垂算法中含有无功增益参数、无功偏差积分系数和与无功微分系数，且参数影响系统的稳定性和动态性能，因此，有必要对提出改性型无功下垂算法中的参数进行优化。首先，在微电网系统中，电压需要保持在一定范围内，否则将影响微电网电能质量；其次，微网中各个微源应合理出力，尽量减少环流。因此，本文选择负荷公共侧电压和环流作为优化指标，尽量保持公共电压接近额定值和无功环流为0 A，得到其目标函数为：

其中：err为与公共母线电压指标有关的电压误差目标函数；|E−1|用来描述公共母线电压偏离额定值的程度；Δerr为与环流指标有关的目标函数；|Q/Q−Q/Q|用于描述微电网中任意2个微源和间的无功偏差程度；bus为公共电压总线的数目，n表示微源的数目；Q表示第个微源的额定无功容量。

赋予每个优化指标权重，以此衡量该指标对系统的重要性。因此，得到改进型无功下垂算法的性能优化目标函数为

其中，目标函数满足的约束条件为

在约束条件中，Kmax是小信号模型中确定的最大电压偏置参数，Kmax是系统临界稳定的最大微分参数。考虑负荷电压偏差和环流指标的同等重要性，赋予的优化指标权重相等，即有1=2=0.5。采用一般的离线搜索方法可求得此目标函数的最优解(q，K，K)，结果如表2所示。

表2 DG单元的电路和控制参数

3 基于改进型无功下垂法的小信号模型

3.1 基于改进型无功下垂法的小信号模型的建立

为便于分析，仍以2台容量相等的并联逆变器为例，建立在稳定平衡点附近的小信号数学模型，讨论并联系统各参数对稳定性的影响，以便为系统控制参数的选择提供依据。

式(7)中，控制功率都是将瞬时功率通过低通滤波器滤波后得到，为简化分析，用一阶滤波器等效代替。利用小信号分析方法，在系统稳定工作点附近给一个很小的扰动，可以得到在工作点附近线性化的结果：

式中：=1，2。对功率方程(3)和(4)进行小信号处理得

将DG1的新型的无功下垂表达式写成

DG2也有类似表达式。DG1的改进型小信号数学模型为

联立式(12)和式(15)，得到DG1的状态矩阵方程为

其中：

将式(13)写成式(17)，并联立DG1和DG2的状态方程组，得到2台并联逆变器的小信号数学模型：

3.2 基于改进型下垂法的小信号模型的分析

本文研究的对象是50 Hz单相逆变器组成的并联系统，逆变器的电气和控制参数如表2所示。将这些参数代入式(18)，可得到基于改进型下垂法的小信号数学模型。图4所示为系统状态矩阵特征根随着控制参数的变化情况。

(a) 参数m(1×10−6＜m1=m2＜1×10−3 rad/J)变化；(b) 参数n(1×10−4＜q1=q2＜1×10−1 V/Var)变化；(c) 参数Kq(1×10−4＜Kq＜1×10−1)变化；(d) 参数Kr(1×10−6＜Kr＜3×10−3)变化

图4(a)和图4(b)所示分别为有功下垂增益从1×10−6radJ变到1×10−3radJ和无功下垂增益从1×10−4VVar变到1×10−1VVar时对应的根轨迹分布情况。显然，增大有功下垂增益，主导极点越来越靠近虚轴，且有1对共轭复极点越来越远离虚轴，系统阻尼减弱，主导极点离虚轴越近，响应速度变慢，且不利于稳定。若增大无功下垂增益，则1对共轭复极点的虚部减小，阻尼增强，但主导极点基本没有变化，对系统的稳定性和响应速度几乎没有影响，也说明基于改进型无功下垂控制方法的稳定性和动态性能对下垂增益不敏感，在提高无功均分精度的同时，没有降低系统稳定性和动态性能。

图4(c)和图4(d)所示分别为电压偏置参数从1×10−4到1×10−1和微分增益从1×10−6变到3×10−3时对应的根轨迹分布情况。当电压偏置在指定的范围内增加时，系统的主导极点将稍微远离虚轴。若电压偏置参数过大，1个实极点将靠近虚轴而成为主导极点，不利于系统的稳定。若电压偏置过小，则1对主导极点将离远点过近，此时，积分时间过大，影响系统的动态性能。当微分参数增加时，导致主导极点靠近零点，不利于系统稳定。因此，电压偏置参和微分参数需合理取值，在保证系统稳定性的前提下，增强系统的动态调节性能。

4 仿真和实验

4.1 仿真验证

基于Matlab/Simulink搭建微电网系统仿真模型，以验证改进无功电压下垂控制策略的可行性。该仿真模型由2台容量相同的DG单元和线性负载组成，DG单元经过馈线接至公共母线。其中各DG单元的电路参数如表2所示。图5所示仅为微电网系统中单个DG控制示意图。

图5 DG单元控制示意图

4.1.1 算例1

采用本文提出的改进型无功电压下垂控制策略，2台相同容量的微源并联运行。图6(a)所示为2个微源无功出力分配的情况。在=4 s之前，微源1的线路电感为0.3 mH，微源2的线路电感为0.6 mH，由于线路上不均衡的电压降导致传统的无功控制不能完全均分负荷无功功率，且微源1输出无功为470 Var，微源2输出无功为400 Var；在=4 s之后，采用改进型下垂控制使微源输出无功均为430 Var。

图6(b)所示为2个微源有功出力分配的仿真结果。由图6(b)可知：各微源输出有功均为2.2 kW，改进的无功控制算法并不影响有功均分。图6(c)所示为2个微源输出电压幅值的变化情况。改进前微源输出电压幅值分别为309 V和308.6 V，改进后微源输出电压幅值分别为309.5 V和308.3 V，微源的输出电压因无功的收敛而使差异变大，但变化幅度在允许范围内。算例1的仿真结果表明：改进型下垂控制算法，在不影响负荷有功均分的条件下，极大地提高微源输出无功的均分精度。

(a) 改进下垂控制时的无功分配情况；(b) 改进下垂控制时的有功分配情况；(c) 改进下垂控制时的DG输出端电压

4.1.2 算例2

本算例用以测试线路参数变化对改进型无功控制算法的影响。在=6 s时，2个微源的线路差异更加明显，DG1单元的线路参数由0.25+j0.062 8变至0.1+ j0.031 4，DG2单元的线路参数不变。图7(a)和图7(b)所示分别为2个微源分别在传统控制和改进控制无功分配的情况。由图7可知：当采用传统下垂控制策略时，微源间的无功偏差约为70 Var，而采用改进型下垂控制策略使得各微源输出无功出现小扰动，但均能稳定输出至430 Var。图7(c)所示为微源输出端电压的幅值变化情况。从图7(c)可见：改进前微源输出电压幅值分别为309.5 V和308.3 V，改进后微源输出电压幅值分别为308.4 V和309.6 V。线路参数的波动影响输出电压的波形，但变化仍在合理范围内。

(a) 传统下垂控制时的无功分配情况(线路参数变化)；(b) 改进下垂控制时的无功分配情况(线路参数变化)；(c) 改进下垂控制时的DG端电压(线路参数变化)

因此，当线路参数发生变化时，传统的下垂控制方法使微源间的无功偏差又发生变化；改进型下垂控制方法则能改善和提高微源输出无功的均分精度，不因线路参数变化而影响其均分度。

4.1.3 算例3

本仿真算例用以分析改进的无功控制算法在负载突变时无功均分效果，进一步验证该方法的有效性。负荷的突变设置如下：在=3 s时，负载增加约为2.0 kW的有功负荷和0.8 kVar的无功负荷；在=6 s时，负载减少约为2.0 kW有功负荷0.8 kVar无功负荷。图8(a)和图8(b)所示分别为2个微源在负荷突变时传统下垂控制和改进型下垂控制作用下的无功分配效果。由图8可知：若采用传统的下垂控制算法，则负荷的波动导致线路压降不平衡，微源间的无功偏差由80 Var增加至100 Var；而采用改进的无功均分算法后，微源间的无功偏差则恒为0 Var。图8(c)显示：在负荷突变时，改进算法使微源间电压差异变大，但变化幅度均在合理的范围内。仿真结果表明：负荷突变时，改进型下垂控制方法仍能保证良好的均分度。

(a) 传统下垂控制时的无功分配情况(负荷突变)；(b) 改进下垂控制时的无功分配情况(负荷突变)；(c) 改进下垂控制时的DG端电压(负荷突变)

4.2 实验验证

在实验室建立一套2台逆变器并联系统验证算法的有效性。主电路开关器件采用CM75DY−24H，控制板核心由DSP 28335和FPGA EP2C8T144C8N构成。具体参数配置为：直流侧电压80 V，主电路参数如表1所示，负载为阻感负载(16 Ω，3 mH)，开关频率和采样频率均为12.8 kHz。图9和图10所示分别为微源稳态运行时输出的电流和环流波形。DG1的线路电感为0.3mH，DG2的线路电感为0.6mH，各微源的输出电压峰峰值约为50 V。通道1为公共负荷侧电压，通道3和4分别为微源输出电流，通道math为系统环流oH=(01−02)。由于微源的参数不一致，采用传统的无功控制方法使得微源输出电流存在较大的相位差，且有一定的电流畸变，此时，系统环流较大，环流0H峰峰值为2.10 A；采用改进型下垂控制方法使得系统环流基本上无相位差，电流畸变明显变小，且环流0H峰峰值趋近于0.15 A，因此，与传统的控制策略相比，提高了无功功率均分的精度。

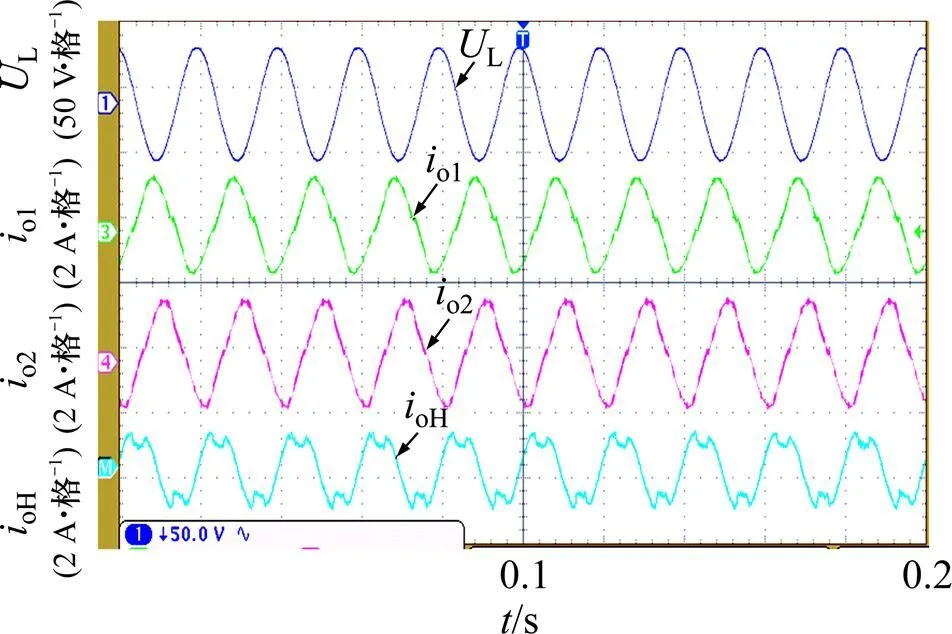
图9 传统控制方法下获得的稳态实验波形

图10 改进型控制方法下获得的稳态实验波形

图11和图12所示分别为微源稳态运行时输出的有功功率和无功功率实验波形。传统控制方法下获得的稳态有功功率分别为31.40 W和30.90 W，获得的稳态无功功率分别为19.80 Var和−10.50 Var；改进型控制方法下获得的稳态有功功率分别为30.60 W和31.10 W，获得的稳态无功功率分别为4.85 Var和4.40 Var。上述结果表明：采用改进型下垂方法在不影响有功功率均分的情况下，微源输出的无功功率均分精度大大提高，从而减小了系统环流。

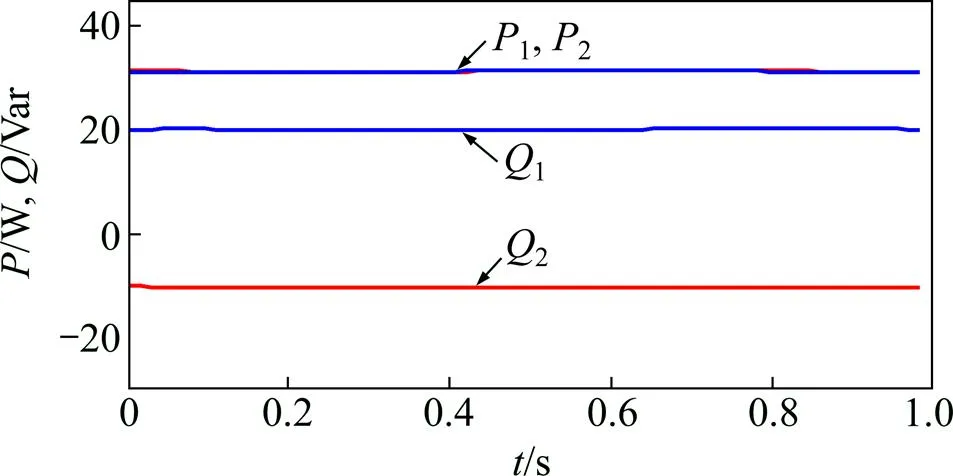
图11 传统控制方法下获得的稳态功率实验波形

图12 改进型控制方法下获得的稳态功率实验波形

图13所示为各微源输出电流及环流(01−02)的波形，截取了加改进型控制策略时刻的暂态过程。在=1.5 s时，加进改进型下垂控制策略。可见：系统环流峰峰值由改进前的2.10 A变至改进后的0.15 A，系统环流大大减小，各微源输出的无功功率由传统控制方法下的20 Var和−10 Var均收敛至5 Var，微源输出无功功率得到合理均分。

图13 各微源输出电流及系统环流波形

图14所示为负载切换时的逆变器输出电流波形和系统环流波形。由图14可知：在=1.5 s之前，微源1和2的输出电流峰峰值约为2.8 A；在=1.5 s之后，微源1和2的输出电流峰峰值约为1.6 A；在不同的负载下，采用改进型下垂控策略使得环流为0.21 A，基本上不变且趋于0，因此，仍然能实现负荷无功的均分，满足稳定性要求，且在切换过程中有较快的动态响应特性，并具有较高的均流性能。

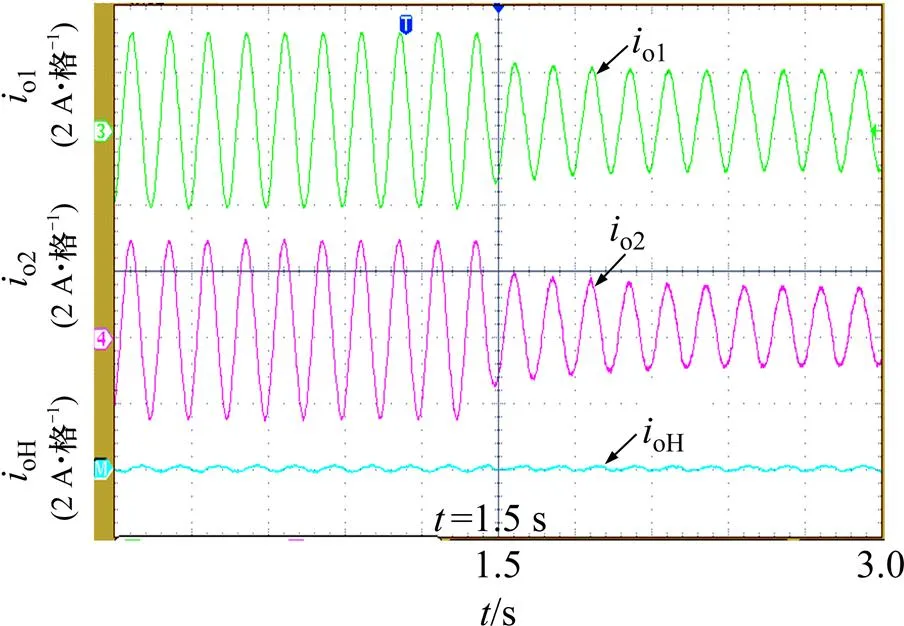
图14 负荷切换时的微源输出电流及环流波形

5 结论

在分析微电网中电压/无功下垂特性的基础上，提出一种改善DG间无功功率均分的控制策略。该方法利用低带宽通信获取各微源的无功功率信息，通过改变传统下垂控制的电压偏置，提高了无功功率均分精度。另外，利用小信号分析方法证明了改进型下垂控制策略的稳定性，为系统参数的设计提供了依据。仿真和实验验证了该方案的有效性和优越性：

1) 极大地提高了分布式微源输出无功功率的均分精度，发挥了微源的最大输出能力。

2) 仅需低带宽通信技术，且通信简单容易实现，对通信实时性和同步性要求不高。

3) 该方案对微电网的结构不敏感，因此，适用于复杂的微电网结构。

[1] 孙元章, 梅生伟. 国际合作, 优势互补, 开拓电力系统科研新领域[J]. 中国科学基金, 2003, 17(3): 185−187.
SUN Yuanzhang, MEI Shengwei．Exploring the new advantages of the electric power system through international cooperation[J]. Science Foundation in China, 2003, 17(3): 185−187.

[2] 鲁宗相, 王彩霞, 闵勇, 等. 微电网研究综述[J]. 电力系统自动化, 2007, 31(19): 100−107.
LU Zongxiang, WANG Caixia, MIN Yong, et al. Overview on microgrid research[J]. Automation of Electric Power Systems, 2007, 31(19): 100−107.

[3] Holtz J, Lotzkat W, Werner K H. A high power multitransistor inverter uninterruptible power supply system[J]. IEEE Transactions on Power Electronics, 1998, 3(3): 278−285.

[4] Martins A P, Carvalho A S. Design and implementation of a current controller for the parallel operation of standard UPSs[C]//IEEE IECON 21st International Conference. Orlando, FL, USA: IEEE, 1995: 584−589.

[5] Sun X, Lee Y S, Xu D. Modeling, analysis, and implementation of parallel muti-inverter system with instantaneous average current sharing scheme[J]. IEEE Transactions on Power Electronics, 2003, 18(3): 844−856.

[6] Guerrero J M, HANG Lijun, Uceda J, et al. Control of distributed uninterruptible power supply systems[J]. IEEE Transactions on Industrial Flectronics, 2008, 55(8): 2845−2858.

[7] Tuladhar A, Jin H, Unger T, et al. Control of parallel inverters in distributed AC power systems with consideration of line impedance effect[J]. IEEE Transactions on Industry Electronics, 2000, 36(1): 131−138.

[8] Cheng P T, Chen C A, Lee T L, et al. A cooperative imbalance compensation method for distributed generation interface converters[J]. IEEE Transactions on Industry Applications, 2009, 45(2): 805−815.

[9] Engler A, Soultanis N. Droop control in LV-grids[C]// International Conference on Future Power Systems. Amsterdam, USA: IEEE, 2005: 1−6.

[10] Brabandere K D, Bolsens B, Keybus J V D. A voltage and frequency droop control method for parallel inverters[J]. IEEE Transactions on Power Electronics, 2007, 22(4): 1107−1115.

[11] LI Yunwei, Kao C N. An accurate power control strategy for power electronics interfaced distributed generation units operating in a low voltage multibus microgrid[J]. IEEE Transactions on Power Electronics, 2009, 24(12): 2977−2988.

[12] 张纯江, 陈桂涛, 祖峰, 等. 一种全数字化互动跟踪式单相逆变电源并联均流控制策略[J]. 中国电机工程学报, 2006, 26(10): 63−66.
ZHANG Chunjiang, CHEN Guitao, ZU Feng, et al. An interactive following current sharing control strategy for single phase paralleled inverters in full digital[J]. Proceedings of the CSEE, 2006, 26(10): 63−66.

[13] ZHANG Chunjiang, CHEN Guitao, GUO Zhongnan, et al. Alternating master salve parallel control research for single phase paralleled inverters based on can bus[C]//Proceedings of IEEE IPEMC’06. Shanghai, China, 2006: 1−5.

[14] Coelho E A A, Cortizo P C, Garcia P F D. Small-signal stability for parallel-connected inverters in stand-alone AC supply systems[J]. IEEE Transactions on Industry Applications, 2002, 38(1): 533−542.

A control strategy of reactive power sharing for parallel distributed micro-sources

LIU Yao, HAN Hua, SU Mei, SUN Yao, CHEN Huibin, LONG Xi

(School of Information Science and Engineering, Central South University, Changsha 410083, China)

For multi-inverters parallel operation in microgrid, the output impedance of inverters and the line impedance between the inverters and point of common coupling are always different, which can result in big circulating current and low precision of power sharing among inverters by using the traditional droop control method. To reduce the circulating current and improve the reactive power sharing accuracy, a novel droop control strategy of reactive power sharing was proposed. The method with low bandwidth communication was employed to modify the voltage bias of reactive power-voltage droop characteristic, so that the reactive power sharing accuracy can be improved. The objective function was proposed with the optimization index of circulate current and load voltage deviation, and the system parameters were optimized and designed. The results show that the improved droop controller can achieve load reactive power precisely without affecting the active power sharing, and it also has a good dynamic and steady-state performance.

microgrid; improved droop control; reactive power sharing; low-bandwidth communication; parameter optimization

TM712

A

1672−7207(2015)02−0525−09

2014−01−22；

2014−04−25

国家自然科学基金资助项目(61174125)(Project(61174125) supported by the National Natural Science Foundation of China)

韩华，副教授，从事分布式发电及其微电网控制技术；E-mail：hua_han@126.com

10.11817/j.issn.1672-7207.2015.02.022

(编辑 陈灿华)