双轴旋转式惯导系统自标校技术

于 飞，孙 骞，张 亚，吕重阳

(1.哈尔滨工程大学 理学院，150001哈尔滨;2.哈尔滨工程大学 自动化学院，150001哈尔滨)

惯性器件逐次启动误差是影响捷联惯性导航系统(strap-down inertial navigation system，SINS)精度的主要因素，因此若保证系统能够长时间具有较高的定位精度，需要在SINS启动后对其进行在线标校［1］.惯导系统在线标校的基本思想是通过改变惯性测量单元(inertial measurement unit，IMU)在空间中的运动形式(包括角运动和线运动)提高系统的可观测性，从而实现惯性器件误差最优估计的目的［2］.对于飞机、导弹等高速运载体改变IMU的运动形式相对容易.但是对水面航行的舰船来说，系泊状态下的其机动可以近似忽略，即使在航行过程中，由于舰船加减速或转弯过程十分缓慢，因此其机动也并不明显.所以直接改变舰船IMU的空间位置并不容易.为了解决上述问题，双轴旋转式SINS应运而生，该系统是利用具有二自由度转位能力的旋转机构，按照特定的转位方案旋转，从而改变IMU的空间位置，大幅提高SINS中惯性器件误差的可观测性［3］.旋转式SINS自标校技术可以被看作一种基于Kalman滤波的系统状态最优估计问题，因此在设计Kalman滤波器之前需要对SINS系统进行可观测性分析［4-5］.传统的可观测性分析方法有分段线性定常系统(piece wise constant system，PWCS)可观测性分析方法［6-7］和奇异值分解(singular value decomposition，SVD)方法［8］等.但这两种方法均有一定的局限性，PWCS方法只能得到系统可观测状态向量的个数，而无法确定其具体的可观测程度;对存在多个状态耦合的不完全可观测系统来说，SVD方法并不能明确指出这种耦合性［9-10］.

针对传统方法的不足，众多学者对可观测性分析方法进行进一步的研究与改进，其中最为显著的改进方法是国防科技大学吴美平等［11］在2011年提出的一种基于原始非线性模型的可观测性分析方法，即全局可观测性分析方法.该方法从可观测性定义入手，以SINS的非线性误差模型作为可观测性分析基本方程组，求解方程组解的形式，进而对SINS进行全局可观测性分析.全局可观测性分析方法避免了传统可观测性分析方法的不足，可以简单、直接、有效地对SINS进行可观测性分析.本文借助该方法的思想建立了多位置驻留及绕旋转轴转动与惯导系统可观测性之间的关系，据此提出了SINS初始对准与自标校转位方案设计原则，并基于该原则设计出一种较优的转位方案，最后通过数字仿真和实验验证了该初始对准与自标校转位方案的有效性和优越性.

1 转位方案设计原则

对于双轴旋转式SINS自标校方案的设计，其关键在于驻留位置的选择及旋转轴的确定.因此本节将分别对转位方案设计的关键技术进行讨论.

1.1 驻留位置的选取原则

假设惯性器件只存在常值偏差，陀螺仪的输出值可表示为

对式(1)进行整理，有

若有3个等半径的球面两两相交，则交点的个数为2，且这两个交点关于这3个球心所成平面对称，所以仅有3个约束条件是不够的.若希望进一步确定出唯一点，则需引入另一个球面，且该球面的球心不在该平面内［12］.因此ε可表示成:

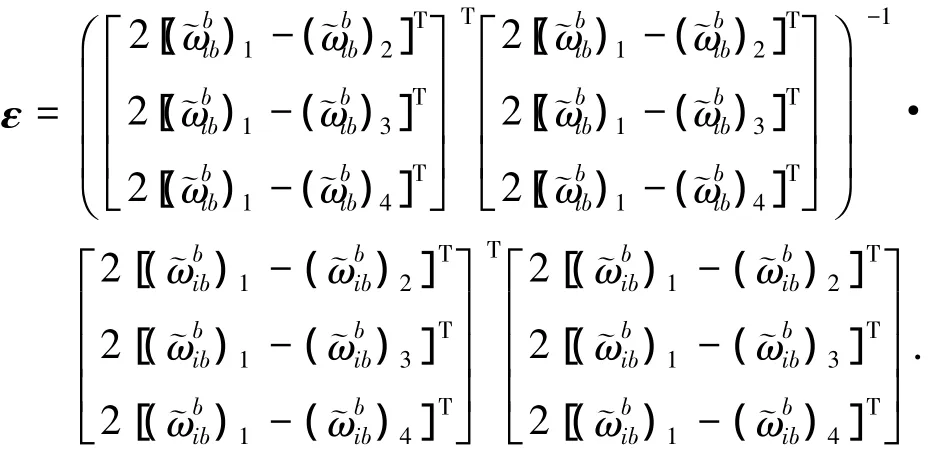
经过上述分析可得驻留位置的选取原则，即IMU至少在4个不同位置驻留时，陀螺漂移、加速度计零偏才能完全可观.

1.2 旋转轴的选取原则

根据惯性导航基本原理有式(3)成立［13］，该式为全局可观测性分析基本方程组.

其中:Cnb为载体坐标系相对于导航坐标系的方向余弦矩阵和分别为加速度计和陀螺仪的实际输出值;ω为地球坐标系相对惯性坐标系的旋转角速度在导航坐标系下的投影;ω为导航坐标系相对地球坐标系的旋转角速度在导航坐标系下的投影;gn为重力加速度在导航坐标系下的投影;vn为载体运动速度在导航坐标系下的投影，静基座条件下为0．

考虑静基座条件下绕IMU敏感轴匀速转动的情况，上式可化简成:

对式(4)进行求导运算，有

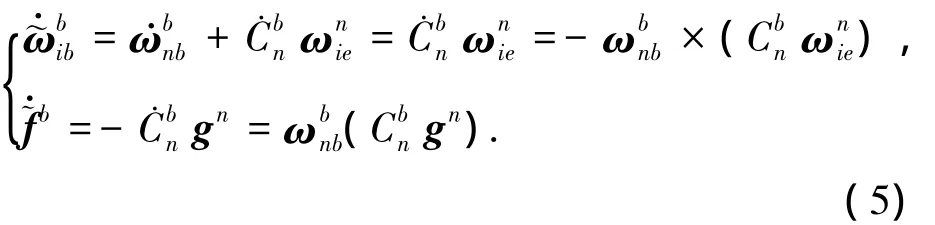
对式(4)进行求二阶导运算，有

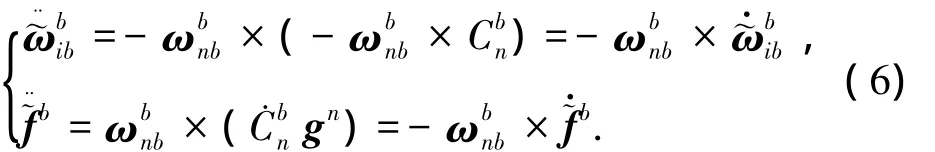
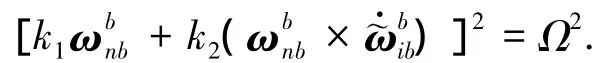
将等式左边展开，有

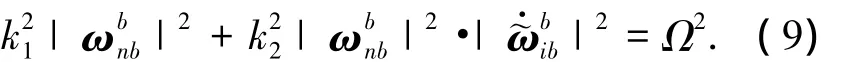
由式(7)和(9)整理得

文献［12］中已对本部分进行了详细推导，本文不再累述，可得

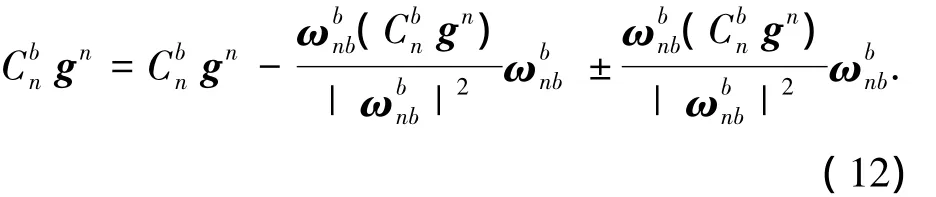
经过上述分析可得旋转轴的选取原则:当旋转轴选取为两水平轴时，陀螺漂移、加速度计零偏均完全可观.

2 初始对准与自标校方案设计

由上节分析可知，IMU绕两水平轴交替旋转并至少在4个不同位置驻留时，陀螺漂移、加速度计零偏及失准角等参数才能够完全可观.为了确保惯性器件误差能够完全可观，并尽量减少旋转机构的转动次数，根据上节所分析的转位原则，本节提出了一种绕两水平轴旋转的八位置标校方案，该方案的转动次序如图1所示.

该方案的具体设计为:由位置1绕xs轴逆时针旋转180°后到位置2;由位置2绕xs轴逆时针旋转90°后到位置3;由位置3绕xs轴顺时针旋转180°后到位置4;由位置4绕xs轴顺时针旋转90°后到位置1;由位置1绕ys轴逆时针旋转90°后到位置5;由位置5绕xs轴顺时针旋转180°后到位置6;由位置6绕xs轴顺时针旋转90°后到位置7;由位置7绕xs轴顺时针旋转180°后到位置8;由位置8绕xs轴顺时针旋转90°后到位置5;由位置5绕ys轴顺时针旋转90°后到位置1．

图1 八位置转位方案

3 仿真及分析

3.1 Kalman滤波方程

建立旋转式SINS的Kalman滤波方程，状态方程为

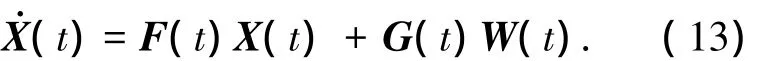
其中:X(t)为SINS系统在t时刻的状态向量;F(t)为SINS系统的状态转移矩阵;W(t)和G(t)分别为系统的噪声向量和噪声驱动阵．

SINS系统的状态向量设置为

系统的噪声向量为

其中:δvE，δvN分别表示东向和北向的速度误差;计算地理坐标系与实际地理坐标系之间东向、北向和天向的误差角分别用φx、φy、φz来表示;▽x、▽y、▽z分别为x、y、z轴加速度计零偏;ω▽x、ω▽y、ω▽z分别为x，y，z轴加速度计的噪声误差;εx、εy、εz分别为x、y、z轴陀螺的常值漂移;ωεx、ωεy、ωεz分别为x、y、z轴陀螺漂移的噪声误差．

以速度误差作为量测量，则SINS的量测方程为

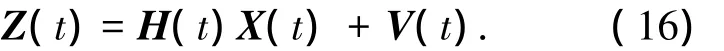
其中Z(t)为t时刻系统的量测向量，H(t)和V(t)分别为系统的量测矩阵和量测噪声．系统的量测矩阵H(t)为

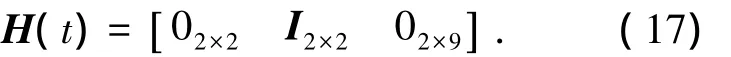
3.2 仿真及结果分析

为了验证所提出的转位方案设计原则的准确性及所设计的绕x、y轴旋转的八位置标校方案的有效性和优越性，设计了三组仿真试验，分别为绕x、y轴旋转的八位置标校试验;绕x、z轴旋转的八位置标校试验;绕y、z轴旋转的八位置标校试验;绕x、z轴和绕y、z轴的转位方案与绕x、y轴旋转的转位方案相同，只是旋转轴不同．仿真参数如表1所示．

表1 仿真参数设置

图2为采用不同转位方案条件下对失准角估计的误差对比曲线.可以看出采用不同的标校方案水平失准角均可在1 h内收敛.而采用绕x、y轴旋转的八位置标校方案，方位失准角误差可在0.7 h内收敛保持稳定，收敛速度明显高于其他两种方案.

图2 SⅠNS失准角误差估计曲线

图3为采用不同转位方案条件下对常值陀螺漂移估计的误差对比曲线.从曲线中可以看出采用绕x、y轴旋转的八位置标校方案，水平陀螺漂移误差可在1 h内收敛并保持稳定;方位陀螺漂移误差也可在1.4 h内收敛.收敛速度和精度都高于其他两种方案.

图4为采用不同转位方案条件下对加速度计零偏估计的误差对比曲线.可以看出采用绕x、y轴旋转标校方案和绕x、z轴旋转标校方案对y轴和z轴加速度计零偏估计效果相当，均可在1 h内收敛;但对x轴加速度计的零偏估计效果，采用绕x、y轴旋转标校方案，可在0.6 h内收敛，明显优于其他两种方案．

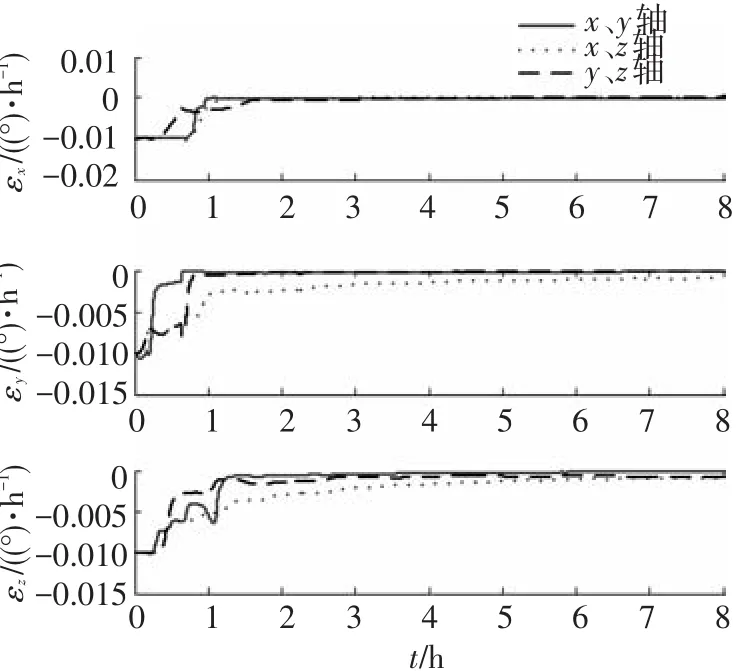
图3 常值陀螺漂移估计误差曲线

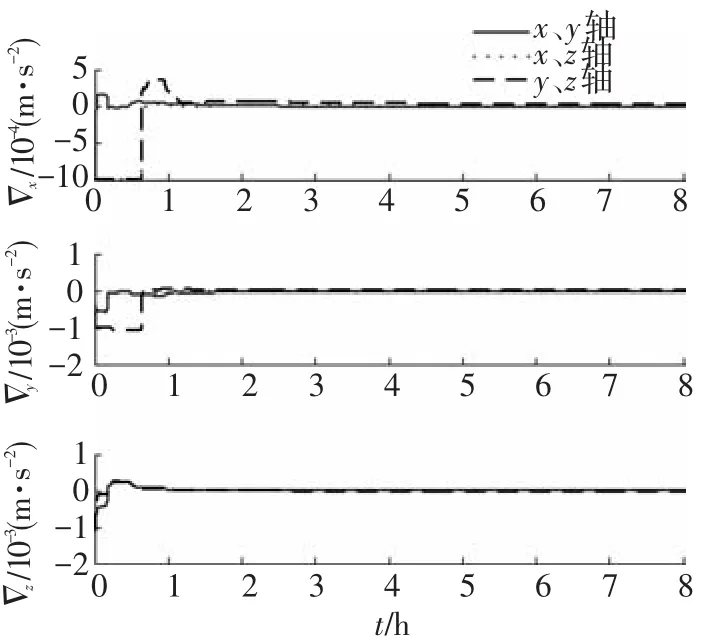
图4 加速度计零偏估计误差曲线

综合仿真曲线及分析可知，采用绕x、y轴旋转的八位置初始对准及自标校旋转方案，系统失准角及惯性器件常值误差的估计效果优于绕x、z轴旋转和绕y、z轴旋转的方案．从而证明了本文所提的转位方案设计原则的正确性及所设计的绕x、y轴旋转的八位置标校方案对惯性器件误差和失准角估计的有效性及优越性．

4 原理样机建立及试验分析

为进一步验证本文提出的标校方案对惯性器件误差的估计效果，开展了实验室试验.实验设备包括哈尔滨工程大学海洋运载器与导航设备研究所研制的光纤陀螺惯导系统和三轴测试转台，如图5所示.为了验证该标校方案的有效性，设计了两组试验，分别为静态条件下SINS自标校试验和绕两水平轴旋转的八位置自标校试验.利用卡尔曼滤波对器件误差及失准角的估计效果进行离线分析.为避免逐次启动误差对试验结果的影响，两组试验之间不重启系统.试验参数如表2所示，两组试验失准角及惯性器件误差的估计曲线如图6～8所示.

表2 试验参数设置

图5 双轴旋转式SⅠNS原理样机

图6 失准角估计效果对比曲线

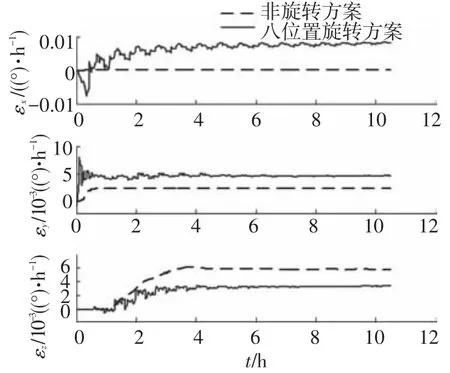
图7 陀螺漂移估计效果对比曲线

图8 加速度计零偏估计效果对比曲线

在实际系统中由于误差未知，进而无法从图6～8的曲线中判断出估计结果的优劣，但是从图中可以看出4 h后采用八位置标校方案的误差估计曲线趋于稳定.为了验证估计出的器件误差及失准角的正确性，把4 h后趋于稳定的估计结果补偿到系统中，通过补偿后系统定位精度的对比，就可以反映出估计效果的优劣，精度对比曲线如图9所示.

图9 器件误差及失准角补偿后系统定位精度对比曲线

从图9中可以看出:补偿由非旋转方案估计出的器件误差及失准角之后，系统的定位精度约为18 nm/10 h;补偿由八位置旋转方案估计出的器件误差及失准角后，系统的定位精度约为5 nm/10 h.由此可以看出本文所提出的双轴八位置初始对准与自标校旋转方案能够有效地估计出惯性器件误差，进一步提高SINS的定位精度.

5 结 语

针对SINS自标校中失准角及惯性器件误差估计精度低、收敛速度慢的问题，本文提出了双轴旋转式SINS自标校转位方案设计原则，并利用该原则设计出了一种八位置标校方案，该方案采用绕两水平轴周期性转停的方式，有效提高了系统的可观测性.数字仿真和试验结果表明利用本文所提出的标校方案能够有效地估计出惯性器件误差及失准角误差，从而有效地抑制惯性器件误差的影响，大幅度提高了SINS的定位精度.但是本文并未考虑惯性器件标度因数误差，因此将进一步研究惯性器件标度因数误差的估计问题.

［1］孙枫，孙伟.基于单轴转动的捷联系统粗对准技术研究［J］.系统工程与电子技术，2010，32(6):1272-1276.

［2］李仁，陈希军，曾庆双.旋转式捷联惯导系统误差分析［J］.哈尔滨工业大学学报，2010，42(3):368-372.

［3］孙枫，曹通，唐李军，等.旋转调制捷联惯导惯性测量组件零偏的估计方法［J］.系统工程与电子技术，2011，33(9):2045-2049.

［4］孙枫，孙伟.旋转捷联惯导系统精对准技术［J］.系统工程与电子技术，2010，32(3):630-633，659.

［5］王小刚，郭继峰，崔乃刚.INS/Vision相对导航系统在无人机上的应用［J］.哈尔滨工业大学学报，2010，42(7):1029-1032.

［6］GOSHEN-MESKIN D，BAR-ITZHACK I Y.Observability analysis of piece-wise constant system，Part I:Theory［J］.IEEE Transactions on Aerospace and Electronic Systems，1992，28(4):1056-1067.

［7］GOSHEN-MESKIN D，BAR-ITZHACK I Y.Observability analysis of piece-wise constant system，Part II:Application to inertial navigation in-flight alignment［J］.IEEE Transactions on Aerospace and Electronic Systems，1992，28(4):1067-1075.

［8］万德钧，房建成.惯性导航初始对准［M］.南京:东南大学出版社，1998:95-135.

［9］孔星炜，董景新，吉庆昌，等.一种基于PWCS的惯导系统可观测度分析方法［J］.中国惯性技术学报，2011，19(4):631-641.

［10］马艳红，胡军.基于SVD理论的可观测度分析方法的几个反例［J］.中国惯性技术学报，2008，16(4):448-452.

［11］WU M，WU Y，HU X，et al.Optimization-based alignment for inertial navigation system:Theory and algorithm［J］.Aerospace Science and Technology，2011，15:1-17.

［12］孙骞.双轴旋转式光纤陀螺捷联惯导系统技术［D］.哈尔滨:哈尔滨工程大学，2013:7-30.

［13］孙枫，孙伟.旋转自动补偿捷联惯导系统技术研究［J］.系统工程与电子技术，2010，32(1):122-125.